基于灵敏度分析的三维结构等几何形状优化方法

陈 龙 张高朋

上海理工大学机械工程学院，上海，200093



基于灵敏度分析的三维结构等几何形状优化方法

陈 龙 张高朋

上海理工大学机械工程学院，上海，200093

以等几何分析为数值分析方法，针对三维结构的线弹性问题，以优化边界控制点坐标为设计变量，通过Coons体插值方法得到插值控制点对优化边界控制点的坐标导数，推导了单元刚度矩阵对控制点坐标变量的形状优化灵敏度方程，并对应力灵敏度和位移灵敏度方程进行了推导。数值算例证明该方法具有较高的优化效率，优化结果良好。

等几何分析；三维结构；形状优化；灵敏度

0 引言

在产品优化设计阶段，根据模拟分析阶段得到的仿真结果，对初始的CAD 模型进行优化设计，得到满足需求的最优CAD 模型，可进一步提高CAD 产品的性能[1-3]。根据现有方法优化的模型对象往往和最初的CAD模型有较大出入。

优化分为尺寸优化、形状优化和拓扑优化三个层次[4]。形状优化以结构的边界形状为优化对象，单元节点坐标为设计变量，通过不断改变边界形状达到提高产品性能的目的[5]。在产品拓扑结构的基础上，进行部分边界形状的定量化描述，属于产品的详细设计阶段。在基于传统有限元方法的形状优化中，通常以有限单元的节点坐标为设计变量，该方法存在以下弊端：①往往需要大量的设计变量描述边界形状；②优化迭代中，各节点独立变动，容易造成网格畸变与扭曲；③几何模型与分析模型不统一，使得数据传递只能单向进行。灵敏度分析是通过求解优化方程中的目标函数和约束函数对设计变量的导数来进行优化迭代更新的[6-7]。

等几何分析方法基于有限元离散思想，将CAD系统采用的非均匀有理B样条用于构建NURBS单元，统一了几何建模和有限元分析的整个过程[8]。将等几何分析用于结构形状优化，即以几何模型控制点作为设计变量，解决了传统形状优化难以处理光滑边界、网格畸变等问题。

在优化设计变量的选择方面，QIAN[9]将控制点坐标和权重同时作为设计变量进行形状优化，推导了敏度方程；SONG等[10]将形状优化过程分为控制点坐标优化和权重优化两步，设计初期将控制点坐标作为设计变量，迭代一定程度后，将权重作为设计变量。网格更新规则方面的研究较少，主要依靠控制点坐标相互之间距离的比例关系进行网格更新，容易引起单元形状的不规则。

为了解决网格迭代更新的问题，本文以三维模型为例，通过Coons插值得到模型内部控制点坐标，籍此由边界控制点坐标对设计变量的导数得到内部控制点坐标对设计变量的导数，维持了整体网格的规整性，最后通过数值算例验证了算法的效率与正确性。

1 B样条表达与等几何分析方法简介

1.1 B样条及NURBS表达

定义节点向量ξ=(ξ1，ξ2，…，ξn+p+1)，则B样条曲线可以定义

(1)

其中，Pi为第i个控制点的坐标；Ni，p为第i个p阶基函数。基函数可由Cox-de Boor递推公式得到，p=0时，

(2)

p>0时，

(3)

类似地，B样条曲面可以定义为

(4)

B样条实体定义为

(5)

NURBS样条为非均匀有理B样条，由B样条发展而来。本文优化对象为三维实体，在此仅给出NURBS实体表达式：

(6)

(7)

式中，p、q、r为NURBS实体三个方向上的节点向量的阶次。

可以看出，若所有控制点处的权重为1，则NURBS退化为B样条。

以单个单元为研究对象，设一单元的基函数向量序列为

R=(R1，R2，…，RL)

(8)

其中，第s(s=1，2，…，L；L为单个单元所含控制点数目)个控制点处基函数表达为

Rs=MiNjQk

s=(k-1)mn+(j-1)n+i

i=1，2，…，nj=1，2，…，mk=1，2，…，l

则有该单元几何场的插值形式：

[x(ξ,η,ζ)y(ξ,η,ζ)z(ξ,η,ζ)]T

(9)

(10)

1.2 三维线弹性问题的等几何分析

本文只针对线弹性问题展开研究。应用最小势能原理，得到

Kq=R

(11)

单元e的单元刚度矩阵为

Ke=∫VeBTDBdV

(12)

三维问题中，单元刚度矩阵Ke可以写为

Ke=∫VeBTDBdV

(13)

式中，B为mnl×6阶矩阵；D为6阶方阵。

等几何分析与传统有限元有几点区别。首先，基函数表达式不同，传统有限元分析多用拉格朗日基函数来离散表达几何模型和位移场，而等几何分析采用B样条作为基函数。其次，等参变换的不同，等几何分析采用等参单元思想，但需要进行物理坐标、参数坐标和母单元坐标之间的映射，而传统有限元的等参变换仅涉及到物理坐标和参数坐标的变换。等几何分析中，每对参数变换对应一个雅可比变换，其中，参数坐标到母单元坐标变换所对应的雅可比变换行列式为

|J2|=(ξi+1-ξi)(ηj+1-ηj)(ζk+1-ζk)/8

(14)

物理单元坐标到参数空间坐标变换对应的雅可比变换矩阵为

(15)

那么母单元到物理单元映射的雅可比行列式为

|J|=|J1||J2|

(16)

为了描述方便，定义两个矩阵

应变矩阵为(矩阵中的零元素均省略)

(17)

则应变矩阵B可由Г矩阵变换元素位置得到。

将式(9)两边同时对 (ξ，η，ζ)求导，等号左边为

(18)

等号右边为

(19)

由式(18)、式(19)可得

(20)

Г、M与J1之间有下式关系：

(21)

通过式(21)，可求得应变矩阵B。

采用高斯积分法对式(13)进行求解，则单元刚度矩阵表达为

(22)

式中，nel为单元总个数；mi、mj、mk分别为i、j、k方向上的高斯积分点的个数；wijk为高斯点处权重值。

通过式(22)求得单元刚度矩阵后，通过组装即可得到总体刚度矩阵。

2 基于等几何分析的形状优化方法

2.1 优化方程描述

结构优化的目标一般为结构的体积或面积最小、结构的刚度最大或柔度最小，约束一般是结构等效应力小于给定值或最大位移小于给定值。本文优化问题定义为，在一定的体积约束下使得结构柔度达到最小。优化方程如下：

(23)

其中，C为优化目标柔度；[αi]为优化设计变量序列，在文中为优化形状边界控制点坐标；V为优化迭代中模型体积；V*为模型体积上限值；[αi]min、[αi]max分别为设计变量的下限值和上限值，Ku=f为离散控制方程；K为刚度矩阵；u为位移列阵；f为载荷列阵。

2.2 优化流程

对于形状优化，首先确定需要进行优化的模型边界曲线或边界曲面，将位于其上的控制点坐标以参数表示，该参数即为优化设计变量，通过Coons插值方法生成模型控制点参数化坐标矩阵。针对该矩阵，逐次求得其对各设计变量的导数矩阵。通过等几何分析程序求得目标函数值及约束函数值和目标函数及约束函数对设计变量的灵敏度。将上述数值代入优化算法进行设计变量的更新，从而得到新的设计变量值，然后进行优化终止条件判断，满足条件则终止优化，否则以新的设计变量进行等几何分析，再次得到更新的设计变量，直至得到最优的设计变量，整个流程如图1所示。

图1 基于等几何分析的形状优化流程图Fig.1 Flow chart of shape optimization based on isogeometric analysis

优化算法是影响形状优化质量和效率的关键，本文选用移动渐近线法(method of moving asymptotes，MMA )。MMA需要输入优化问题的目标函数和约束方程对设计变量的导数，因此需要通过等几何分析程序求得该导数，即敏度信息。每次优化迭代中，MMA通过等几何分析计算得到的敏度矩阵更新设计变量值。然后根据迭代终止条件判断优化结果是否满足收敛，若不收敛，则继续优化，直至得到最优设计变量值。

2.3 Coons插值法获得控制点坐标

形状优化的设计变量一般为边界曲面上的控制点坐标，为了得到等几何分析所需的控制点网格，需要在边界曲面内部进行插值。如图2所示，已知实体边界面上的控制点，通过Coons体插值，得到实体内部所有控制点坐标。设某边界面控制点为Pi，j，k(i=1，2，…，l；j=1，2，…，m；k=1，2，…，n)，设l为u方向控制点数目，m为v方向控制点数目，n为w方向上的控制点数目。令

u0=(i-1)/(m-1)u1=1-u0

v0=(j-1)/(n-1)v1=1-v0

w0=(k-1)/(n-1)w1=1-w0

图2 孔斯体插值方法Fig.2 Coons body interpolation method

那么内部控制点可由边界控制点通过下式求得：

Pi,j,k=u1P0,j,k+u0Pl,j,k+v1Pi,0,k+v0Pi,m,k+

(24)

求得边界控制点坐标对设计变量的导数后，基于式(24)可以得到模型所有控制的点坐标对设计变量的灵敏度：

(25)

2.4 单元刚度矩阵对设计变量的灵敏度方程推导

灵敏度分析首先要求得离散控制方程(式(22))对设计变量的导数。整体刚度矩阵K是由单元刚度矩阵组装而来的，因此转化为求单元刚度矩阵Ke对设计变量导数问题。对设计变量求导得

(26)

根据式(26)，需要计算B及|J|对设计变量的导数，首先计算B对αi的导数。

式(20)、式(21)两边同时对设计变量求导有

(27)

(28)

将式(28)代入式(27)得

(29)

(30)

通过式(30)求得∂Γ/∂αi后，将∂Γ/∂αi矩阵中元素进行互换位置即可得到∂B/∂αi。接着需要计算

(31)

本文模型所加载荷不受设计变量变化的影响，故单元载荷列阵fe对设计变量导数为0，即∂fe/∂αi=0。将式(29)、式(31)代入式(26)即可求得单元刚度矩阵对设计变量的导数。

求得单元刚度矩阵对设计变量灵敏度后，通过单元刚度矩阵组装成总体刚度矩阵的方法，得到总体刚度矩阵对各个设计变量的灵敏度矩阵，进而求得优化方程中目标和约束方程对设计变量的灵敏度。

2.5 目标函数和约束函数对设计变量的灵敏度方程推导

在已知优化方程(式(23))的情况下，可以对下列灵敏度方程进行求解。

(1)结构柔度对设计变量的灵敏度：

(32)

(2)体积对设计变量的灵敏度：

(33)

(3)指定点位移对设计变量的灵敏度：

(34)

其中，行向量e除第i个元素为1外，其余元素均为0。那么通过式(34)即可得到位移向量中第i个位移值对设计变量的导数。

(4)指定点应力分量对设计变量的灵敏度：

(35)

(36)

其中，λ为Kλ=(DBe)T的解。

(5)等效应力对设计变量敏度：

(37)

令

则有

(38)

等效应力对设计变量的导数为

(39)

将式(36)中应力分量对设计变量的敏度代入式(39)即可求得等效应力对设计变量的敏度。

3 数值算例分析

3.1 变截面悬臂梁形状优化

首先为了表述方便，将模型控制点通过集合的形式进行描述，将坐标分量符合条件L0≤L≤L1且W0≤W≤W1且H0≤H≤H1的控制点P(L，W，H)定义为{P(L，W，H)|L∈[L0，L1]，W∈[W0，W1] ，H∈[H0，H1]}，其中，L0、L1、W0、W1、H0、H1均为常数值。

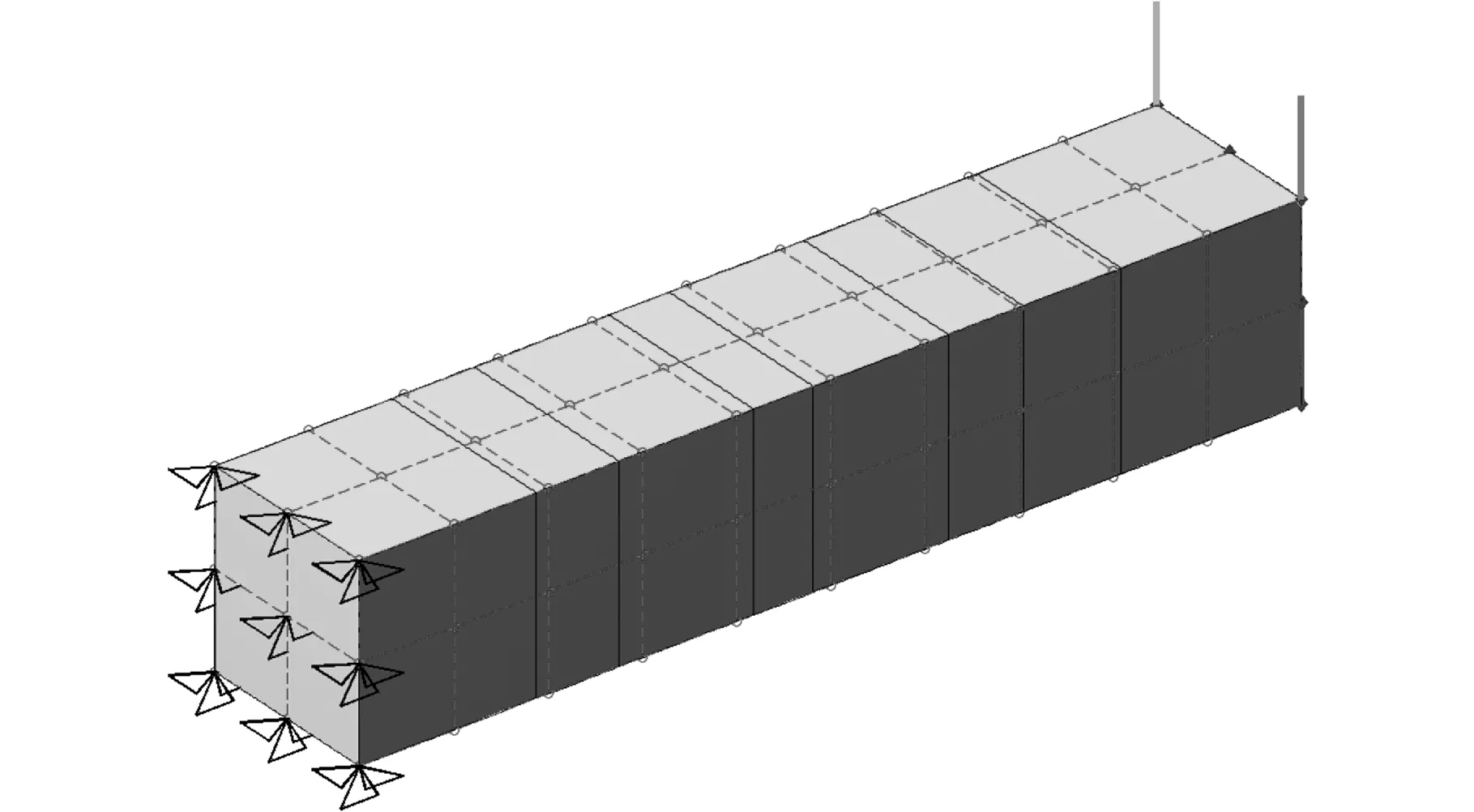
图3 模型初始形状及边界条件(悬臂梁)Fig.3 Initial shape of model and boundary conditions (cantilever beam)

如图3所示，模型长度方向的节点向量u=(0，0，0，0，0.1，0.2，0.4，0.5，0.6，0.7，0.8，0.9，1，1，1，1) ，宽度方向节点向量v、高度方向节点向量w均为(0，0，0，1，1，1)。控制点数目u×v×w=11×3×3。材料的弹性模量E=1.5 MPa，泊松比μ=0.3。载荷与边界条件：模型左端面上控制点{P(L，W，H)|L=0，W∈[0，2]，H∈[0，2]}完全固定，右端面上控制点{P(L，W，H)|L=10，W∈[0，2]，H∈[0，2]}均受到沿H轴负方向的载荷F=-2 mN。优化设计变量：取下底面上控制点{P(L，W，H)|L∈[0，10]，W∈[0，2]，H=0}的H坐标为设计变量。设置对称约束条件：控制点{P(L，W，H)|L∈[0，10]，W∈[0，2]，H=0}与控制点{P(L，W，H)|L∈[0，10]，W∈[0，2]，H=2}关于面H=1对称。优化目标为柔度最小化，约束为体积V≤V0=40，优化的最终形状如图4所示。图5显示了优化迭代过程中，柔度和模型体积的变化。通过表1可知，在体积不增加的情况下，柔度降低了40%。

图4 最终优化结果(悬臂梁)Fig.4 Final optimization results(cantilever beam)

(a)柔度

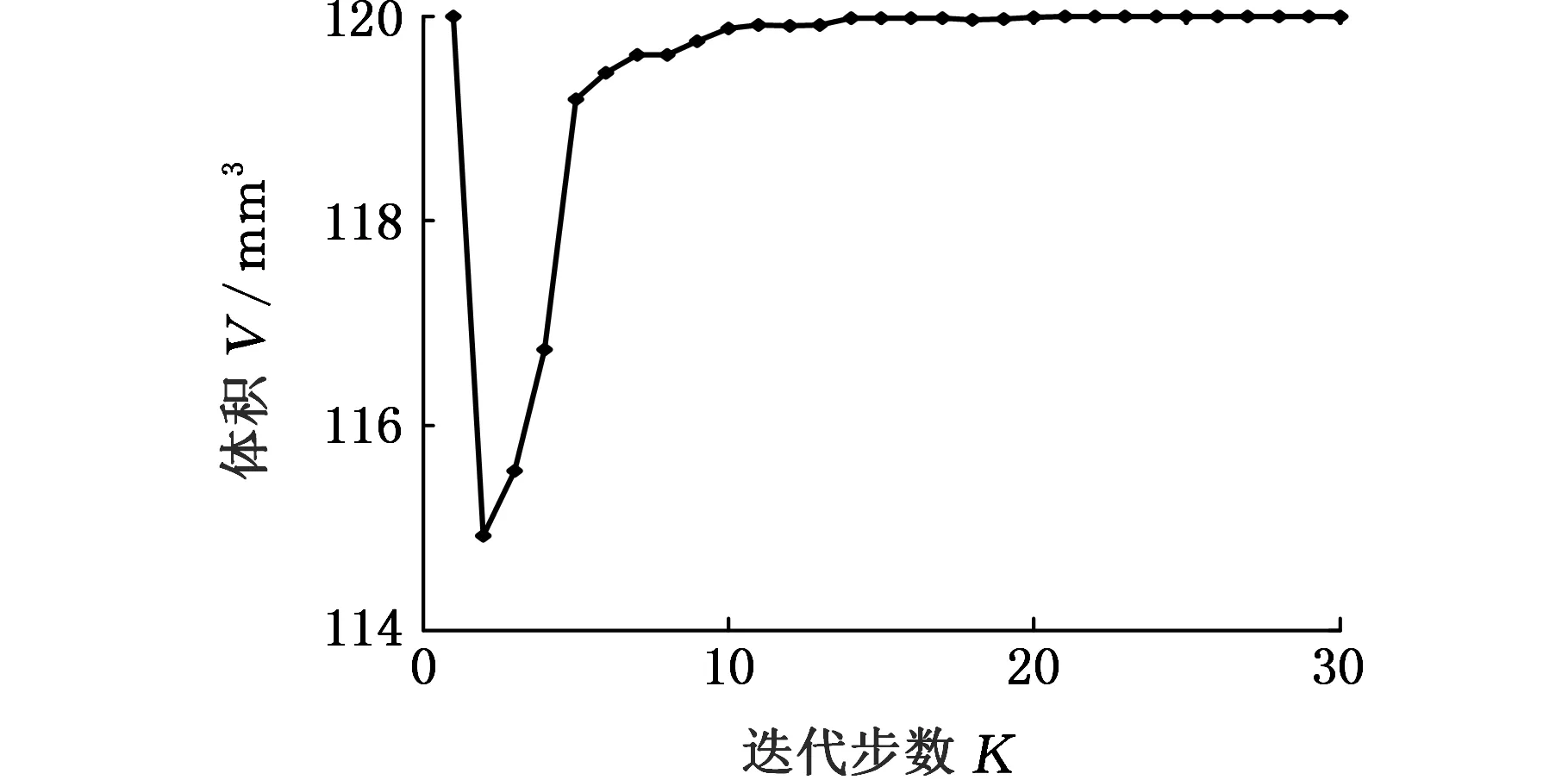
(b)体积图5 迭代曲线(悬臂梁)Fig.5 Iterations(cantilever beam)

柔度(J)体积(mm3)优化前0．052840优化后0．032240

3.2 两端固支梁形状优化

该例沿用例3.1中关于控制点的表述方法。

图6 模型初始形状及边界条件(固支梁)Fig.6 Initial shape of model and boundary conditions (built-in beam)

如图6所示，模型节点向量u=(0，0，0，0，0.1，0.2，0.4，0.5，0.6，0.7，0.8，0.9，1，1，1，1) ，v=(0，0，0，1，1，1)，w=(0，0，0，0.33，0.66，1，1，1)。控制点数目u×v×w=11×3×5。材料的弹性模量E=1.5 MPa，泊松比μ=0.3。载荷与边界条件：左端面上控制点{P(L，W，H)|L=0，W∈[0，2]，H∈[0，4]}和右端面上控制点{P(L，W，H)|L=15，W∈[0，2]，H∈[0，2]}完全固定，上底面上控制点{P(L，W，H)|L∈[0，15]，W=1，H=4}受到沿H轴负方向的载荷F=-100 mN。优化设计变量：控制点{P(L，W，H)|L∈[0，15]，W=0，H=[0，4]}的W坐标为设计变量。设置优化对称约束，控制点{P(L，W，H)|L∈[0，15]，W=0，H=[0，4]}与控制点{P(L，W，H)|L∈[0，15]，W=2，H=[0，4]}关于面W=1对称。优化目标为柔度最小化，约束为体积V≤V0=120，优化的最终形状如图7所示。图8显示了优化迭代过程中，柔度和模型体积的变化。通过表2可以得到，体积不增加的情况下，柔度降低了23%。

图7 最终优化结果(固支梁)Fig.7 Final optimization results(built-in beam)

4 结语

本文的形状优化分别以柔度和体积为目标和约束，以单片NURBS三维模型为优化对象，基于等几何分析推导了形状优化的灵敏度方程，并通过具体实例证明了方法的可行性，结果表明优化收敛速度较快，形状边界光滑。

将等几何分析应用于形状优化，统一了产品的设计、分析和优化过程。NURBS基函数的应用使得和CAD系统的交互更加便捷，可以得到无限光滑的模型边界，省去了优化迭代中复杂的网格重划分操作。今后将根据结构具体失效形式，选取局部应力、最大等效应力或局部位移为约束条件。在优化模型拓扑复杂度方面，将以多片NURBS构成的复杂拓扑结构为优化对象。

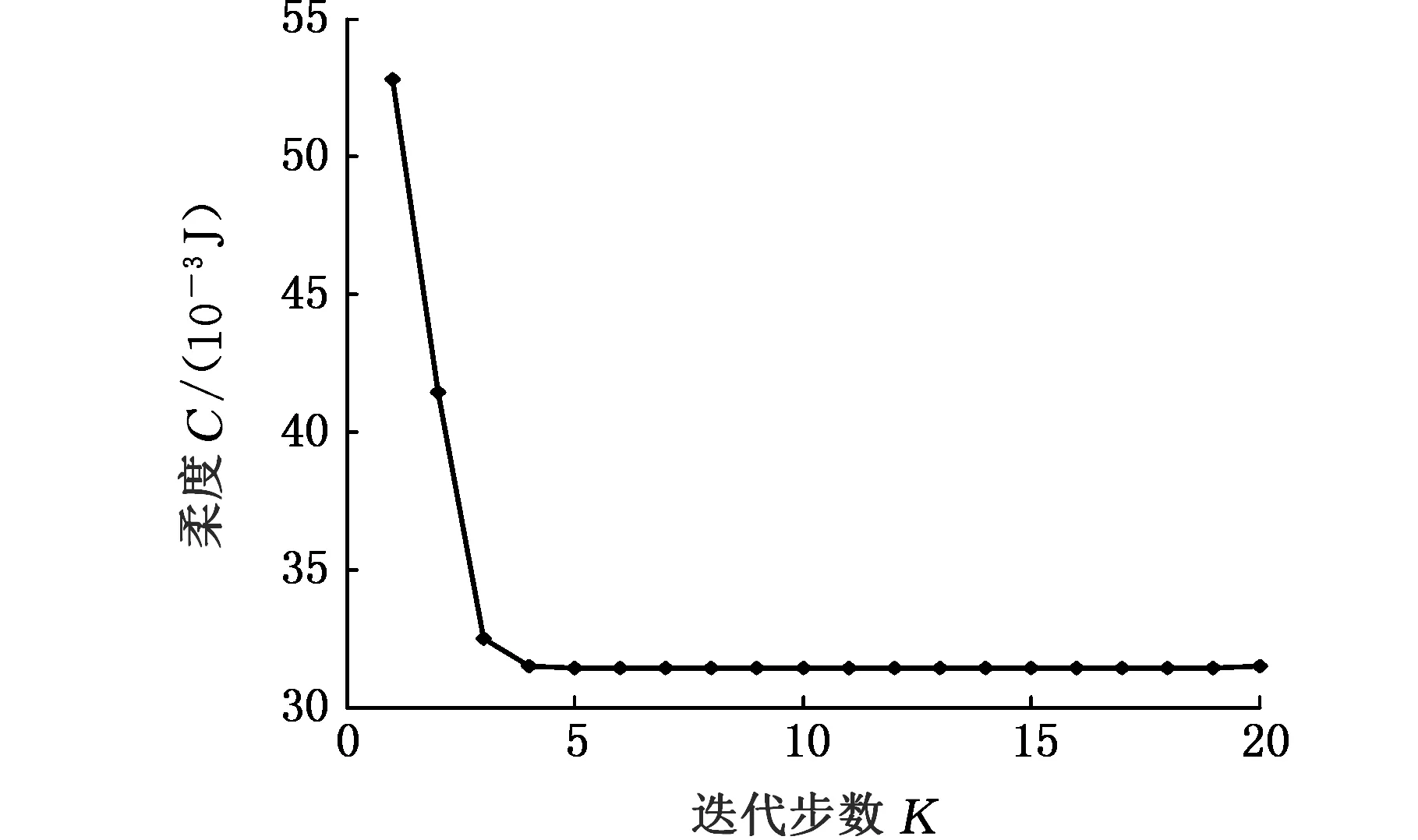
(a)柔度

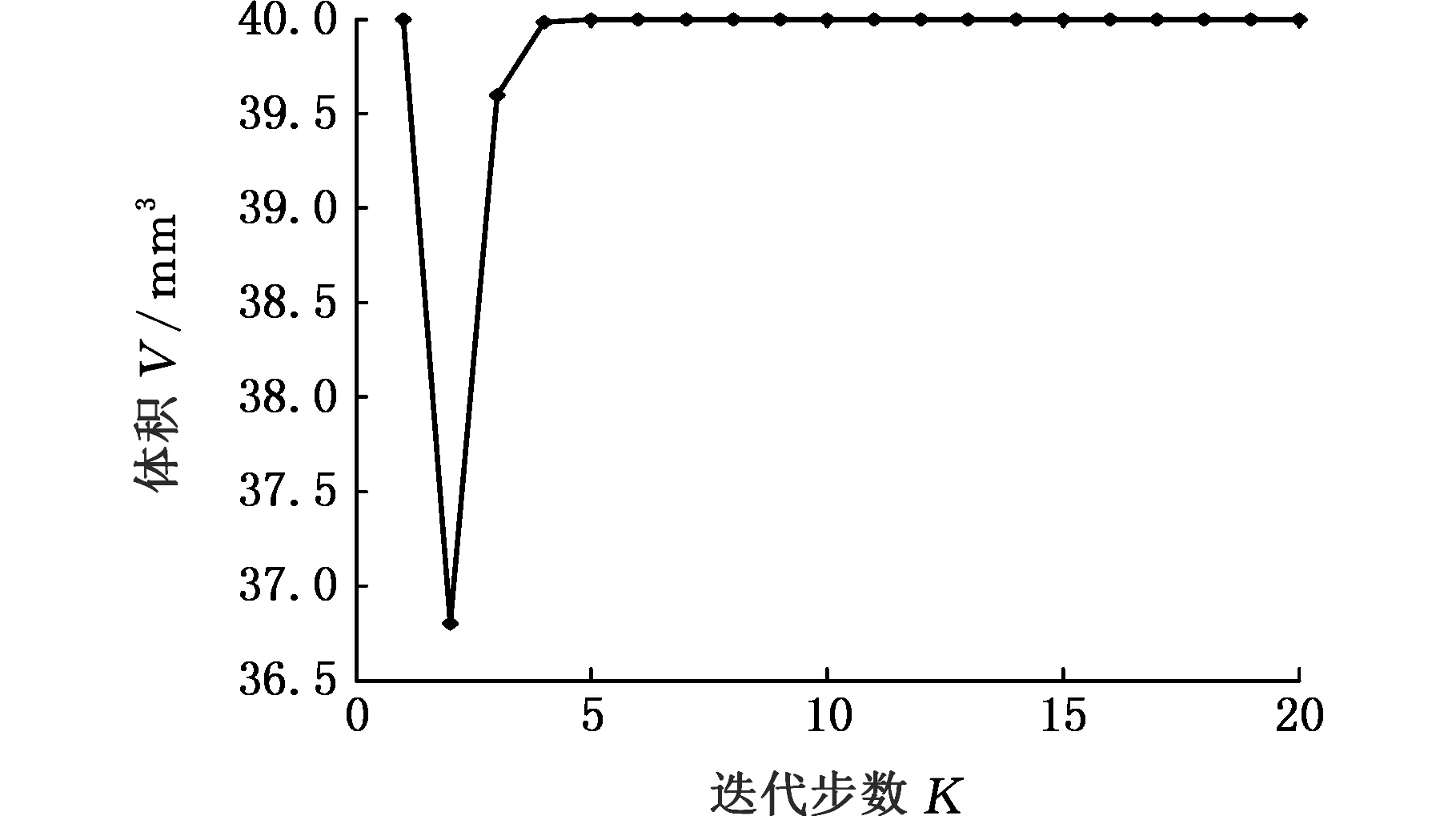
(b)体积图8 迭代曲线(固支梁)Fig.8 Iterations(built-in beam)

柔度(J)体积(mm3)优化前0．5886120优化后0．4531120

当然，Coons插值方法并不能针对所有模型生成适合等几何分析的参数化模型，尤其是在模型比较复杂的时候，需要引入控制点优化算法，而针对这些优化的控制点，如何求解其灵敏度矩阵将是下一步研究的方向。

[1] QIAN X. Topology Optimization in B-spline Space[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 265: 15-35.

[2] CHRISTENSEN P W, KLARBRING A. An Introduction to Structural Optimization[J]. Solid Mechanics & Its Applications, 2008, 153(1):121-146.

[3] WALL W A, FRENZEL M A, CYRON C. Isogeometric Structural Shape Optimization[J]. Computer Methods in Applied Mechanics & Engineering, 2008, 197(33/40): 2976-2988.

[4] HASSANI B, TAVAKKOLI S M, MOGHADAM N Z. Application of Isogeometric Analysis in Structural Shape Optimization[J]. Scientia Iranica, 2011, 18(4):846-852.

[5] NAGY A P, ABDALLA MM, GÜRDAL Z. Isogeometric Sizing and Shape Optimization of Beam Structures[J]. Computer Methods in Applied Mechanics & Engineering, 2006, 199(17/20):1216-1230.

[6] 李初晔， 王卫朝， 马岩. 基于参数灵敏度的结构性能优化[J]. 中国机械工程， 2011, 22(4):397-402. LI Chuye, WANG Weichao, MA Yan. Structural Capability Optimization Based on Sensitivity of Parameters[J]. China Mechanical Engineering, 2011, 22(4): 397-402.

[7] 李蕾，张葆，李全超，等. 基于灵敏度数的薄板结构加强筋布局优化设计[J]. 中国机械工程，2016，27(9): 1143-1149. LI Lei, ZHANG Bao, LI Quanchao, et al. Stiffener Lay Out Optimization of Thin Plate Structures Based on Sensitivity Number[J]. China Mechanical Engineering, 2016, 27(9):1143-1149.

[8] NGUYEN V P, ANITESCU C, BORDAS S P A, et al. Isogeometric Analysis: an Overview and Computer Implementation Aspects[J]. Mathematics & Computers in Simulation, 2012, 117:89-116.

[9] QIAN X. Full Analytical Sensitivities in NURBS Based Isogeometric Shape Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2010，199(29/32): 2059-2071.

[10] SONG Y U，HUR J Y，YOUN S K. 2D Isogeometric Shape Optimization Considering both Control Point Positions and Weights as Design Variables[C]//10th World Congress on Structural and Multidisciplinary Optimization. Orlando, 2013:1-8.

(编辑 张 洋)

Three Dimensional Structural Shape Optimization Based on Sensitivity Analysis UsingIsogeometric Analysis

CHEN Long ZHANG Gaopeng

School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai,200093

An isogeometric analysis method was used as numerical analysis method. As for three-dimensional structures of linear elastic problem, boundary control points that needed to be optimized were regarded as design variables, derivatives of internal control points as to design variables might be obtained by using Coons interpolation method. In shape optimization, sensitivity equation of element stiffness matrix as to control points coordinates was derived, and sensitivity equations of stresses and displacements were deduced. Numerical examples show that the method has high efficiency and good results.

isogeometric analysis; three-dimensional structure; shape optimization; sensitivity

2016-08-24

国家自然科学基金资助项目(51475309,61472111 )

TB121

10.3969/j.issn.1004-132X.2017.14.015

陈 龙，男，1978年生。上海理工大学机械工程学院副教授。主要研究方向为产品计算设计、图像处理。发表论文30余篇。E-mail: wwwchenl@163.com。张高朋，男，1991年生。上海理工大学机械工程学院硕士研究生。