无序效应对1T-TaS2材料中Mott绝缘相的影响∗

赵洋洋 宋筠

(北京师范大学物理学系,北京 100875)

无序效应对1T-TaS2材料中Mott绝缘相的影响∗

赵洋洋 宋筠†

(北京师范大学物理学系,北京 100875)

(2016年10月24日收到;2016年11月21日收到修改稿)

电子强关联效应使得过渡金属硫化物1T-TaS2在低温时为Mott绝缘体,而层间堆叠错位及杂质又会引入相当强的无序效应.利用统计动力学平均场理论数值方法研究了无序效应对Mott绝缘相的影响,发现非对角跃迁无序和对角无序效应均不会引起从绝缘体到金属的相变.杂质引入的对角无序达到一定强度后Mott能隙会完全闭合,而堆叠错位引入的非对角跃迁无序不论多强都无法关闭Mott能隙.在半满情况,非对角无序会导致上下Hubard带对称地分别出现一个奇异态,而通过晶格尺寸标度研究证明了这种反常的电子态仍然是Anderson局域态.

动力学平均场理论,Mott绝缘相,Anderson局域化,非对角跃迁无序

1 引 言

Mott金属-绝缘体转变完全由电子关联驱动,是凝聚态物理学的核心问题之一,又因与高温超导的密切关联而被广为关注[1].迥然相异,Anderson金属-绝缘体转变则是由于体系中存在随机分布的无序势场,当无序强度达到临界值时会导致费米面处的电子态发生实空间局域化[2],从而引发金属-绝缘体相变.相较而言,关联与无序的共同效应经过多年的研究仍然是一个未解决的难题,特别是 Mott和 Anderson两种不同类型的金属-绝缘体转变如何相互影响和竞争,目前仍存在着很大的争议[3].而本文中所研究的层状过渡金属硫化物1T-TaS2体材料为我们解决上述争议提供了一个极佳的实验平台,实验和理论研究均证实,这一材料中不仅存在着很强的电子-电子相互作用,而且层间堆叠错位的无序效应极为显著,此外还存在杂质所引入的随机势场的影响[4],因此是研究关联和无序相互作用的最佳候选材料之一.

1T-TaS2材料会随着温度的变化呈现出非常丰富的量子相,其中包括了多种复杂的电荷密度波 (charge density wave,CDW)相[5,6].特别是在低温区伴随着相变的发生,会出现一个公度的(commensurate)电荷密度波 (CCDW)相,并且样品的电阻也会随之急剧跳变[7],预示着金属-绝缘体转变的发生.针对这个相变,一些学者提出正是由于电子间的强关联导致了材料在CCDW相呈现出Mott绝缘体特征[5,8,9].而最近的角分辨逆光电子谱(angle-resolved inverse-photoemission spectroscopy,ARIPES)实验进一步证明了 Mott相的存在,实验发现1T-TaS2的态密度在费米面处有一个约200 meV能隙[6],并认为采用半满的Mott-Hubbard模型完全能够合理地解释相关的实验发现.

另一方面,尽管在高温区无晶格畸变的 1TTaS2体材料的层间堆积是完好的AA类型,即在c方向上每个钽原子的正上方均是上一层中的钽原子.而在低温区的CCDW相中,伴随着晶格的变形,层间的堆积方式也会随之完全改变.一些实验研究已确认了层间堆叠错位的存在,证实了c方向的钽原子排序具有随机分布特征[10],从而会引入较强的无序效应.而最近,Lahoud等[4]的实验和理论结合研究提出了一个奇特的预见,他们认为通过无序效应能够使得TaS2材料相变到一个新奇的金属态,即体系会通过无序效应而从Mott绝缘体转变为金属.由于这一预言与Anderson的局域化理论相冲突[2],因而也引起了很多的质疑.尽管他们在实验研究中观察到了Mott能隙的关闭以及电阻的降低,但相关的理论计算是基于平均场近似[4],并且缺乏实空间的标度研究,理论结果的可靠性不能保证,因而需要开展更为深入的理论研究.

本文采用统计动力学平均场理论[11]来研究1T-TaS2体材料中关联和无序对量子态的共同效应.本理论方法的优势为,不仅能够合理地考虑电子间的强关联效应,而且能够有效地分析 Anderson局域化效应.我们基于 CCDW 相的实验和第一性原理计算结果构建了一个描述1T-TaS2的Anderson-Hubbard模型,并重点比较了杂质引入的对角无序和层间错位堆叠引入的非对角跃迁无序的作用,以及它们与电子关联间的竞争和共同效应.发现只要对角无序达到足够强时就能够完全关闭Mott能隙,但体系中的电子态因强无序效应而发生Anderson局域化.同样地,非对角跃迁无序也不会引入绝缘体到金属的转变,因为即使无序强度达到最大极限也无法关闭Mott能隙.通过细致的实空间标度研究证明了,包含无序的1T-TaS2体材料体系只能处于Mott绝缘态或Anderson绝缘态,不会发生由无序诱导的从Mott绝缘态到金属态的转变.

2 二硫化钽材料的Anderson-Hubbard模型

1T-TaS2材料是具有“三明治”结构的层状化合物[12],其中钽层位于“三明治”的中心,夹在两个硫层之间.在温度低于180 K时,钽层会发生畸变而生成 CCDW 相,即形成“Star-of-David”结构的的超晶格团簇[5],每个团簇中有三种不同类型的钽原子:中心的 A类原子、外层的6个B类原子及最外层的6个C类原子.除了中心的A类钽原子,其余的12个钽原子的5d轨道电子配对形成“star-bonding”轨道,因而材料的电子结构完全由A类钽原子的外层5d轨道电子决定.因受八面体晶体场影响,5d轨道会劈裂成为三个t2g态(dz2,dxy,dx2−y2)和两个 eg态(dyz,dzx).ARIPES实验发现[6],CCDW相的态密度在费米面处存在一个约为200 meV的能隙,而钽原子的dz2轨道对费米面附近的态密度贡献占主导.由于这一轨道只有一个电子而处于半满状态,因而在电子关联的作用下就会劈裂为上下两个Hubbard子带而处于Mott绝缘相[6].鉴于此,Mott-Hubbard(MH)模型被认为是描述1T-TaS2材料的CCDW相的一个合理的模型[13,14].

由于团簇变形后的中心钽原子在面内的跃迁积分非常小,我们可以忽略面内跃迁项而只重点关注面间跃迁项的影响,得到了一个一维的MH模型,其哈密顿量为:

由于在CCDW相晶格畸变导致了层间堆叠错位[10],这时上下层间的中心钽原子实际距离就会出现随机分布的情况,从而对相应的dz2轨道电子沿着c方向的跃迁积分的大小有着显著的影响.为了研究层间堆叠无序的影响,模型中需要引入一个非对角的跃迁无序项.此外,Lahoud等[4]的实验研究认为杂质同时也会引入对角无序效应,因此可采用如下的密顿量来展现材料中的Anderson无序效应,

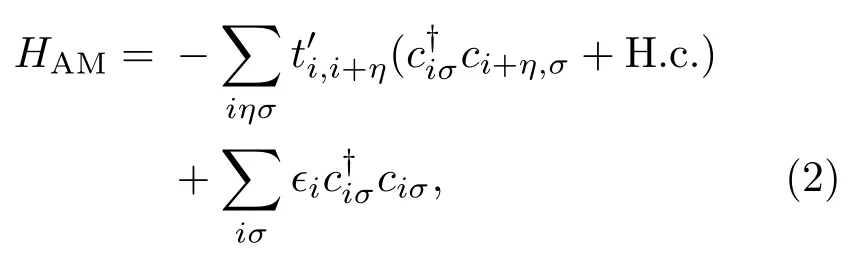
综上,对应1T-TaS2体材料的CCDW相我们既需要考虑电子间的关联,又需要关注无序效应,因此我们建立了一个由(1)式和(2)式共同组合而成的一维Anderson-Hubbard模型,即

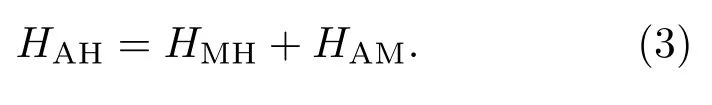
3 统计动力学平均场理论

统计动力学平均场理论[11]是研究强关联与无序的共同效应的一个非常有效的理论数值方法.而一般的动力学平均场理论[15]是将晶格模型(如Hubbard模型)映射为一个单杂质模型,通过建立自洽方程来求解出格林函数.其主要的优点是能准确描述由关联驱动的 Mott金属-绝缘体转变,但由于忽略了空间涨落,不能用于研究无序效应.相对应的,统计动力学平均场理论将单杂质格林函数扩展为晶格的格林函数矩阵[11],能够准确地把握体系的空间涨落及合理地描述实空间中电子态的Anderson局域化.因此,统计动力学平均场理论能够展现 Mott和 Anderson两种不同的金属-绝缘体相变,并适合于研究其二者之间的竞争关系.

将统计动力学平均场理论[11]应用于1T-TaS2的 Anderson-Hubbard模型 ((3)式),体系的格林函数矩阵具有如下形式：

式中所有矩阵的维度均为N(N为格点数).其中为单位矩阵,为跃迁矩阵,包含非对角跃迁无序项,代表对角无序,(ω)是体系的自能,其对角元Σi(ω)对应格点i的内能.

在统计动力学平均场理论的自洽计算中,先通过给定的一个初始内能矩阵可以构建每个杂质格点的Weiss平均场,即无相互作用杂质格点的格林函数

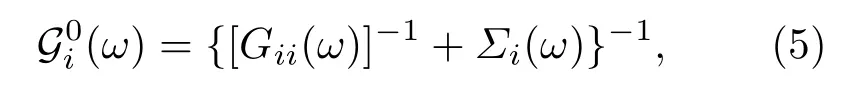
这里的Gii(ω)和Σi(ω)分别是(ω)和(ω)的矩阵元.之后可以采用不同的杂质求解器[15]来求解有相互作用时的完整格林函数为Gi(ω),再通过自洽关系得到新的自能,并进行自洽迭代最终自洽求解出格林函数矩阵.这里,我们采用Hubbard-I近似代替杂质求解器,可直接得到如下自能表达式:

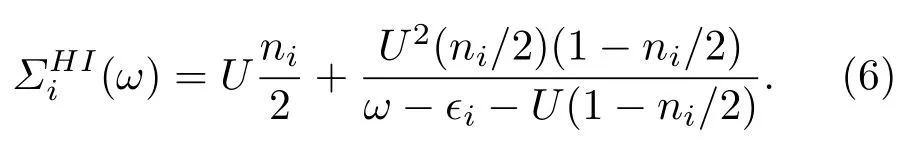
其他自洽步骤不变,也是通过反复迭代得到目标格林函数G(ω)[11].依据实空间的格林函数矩阵,我们就可以直接地讨论电子态的Anderson局域化,以及电子关联对它的影响.

4 计算结果与分析

4.1 不同类型的无序效应的单独影响

前面已经介绍到,我们的理论模型中包含有两种不同类型的无序:一类称为对角无序，是由内部杂质导致势场的随机分布而引入的,其无序强度用W来表示;而另一类是非对角无序,即模型中电子跃迁项的大小也具有了随机分布特征,这代表了1T-TaS2体材料中层间堆叠错位所引入的无序效应,其强度用W′表示.为简单起见,首先在没有相互作用(U=0)情况下,比较这两类无序效应分别对体系态密度的影响,以及它们的共同作用和相互竞争关系,计算结果如图1所示.

这两种不同类型的无序效应的影响差异非常显著,如图1(a)和图1(b)所示.随着对角无序强度W的增强,态密度的带边峰逐渐降低,使得态密度的能量分布趋于平均,并且能带宽度也有显著的展宽.针对包含对角无序的一维体系的标度理论研究[16]已经证明系统中所有的电子态都是处于Anderson局域化的.与之相对应,当只考虑非对角跃迁无序效应时发现,除了能带宽度会随着无序强度W′的增强而有拓宽的趋势外,一个最为显著的特征是出现在能带中心的奇异峰.这个奇异态曾经引起理论的广泛争议,一些早期的理论研究认为处于能带中心ω=0的奇异电子态是扩展态[17],因为一些常规的标度研究表明该奇异点处的局域化长度是发散的[17,18].然而其他一些理论研究否定了上述推断,并最终严格地证明了这个奇异态是一种特殊的局域态[19,20],而电导测量结果也表明材料依然处于局域态.Thouless[21]证明了一维体系中态密度与局域化长度有着直接的联系.依据Thouless的理论,态密度中出现奇异峰是由于能带中心的电子态的局域化长度发生了突变,这一点将在随后的有关晶格尺寸标度的研究中会有更详细的讨论.

为什么目前还没有实验观察到态密度中存在奇异峰的情况呢?为了弄清这一点,我们进一步研究了两种不同类型无序效应同时存在的情况,结果如图1(c)所示.我们特别选取了非对角跳跃无序强度取很大值W′=1.5的情况,这时的奇异峰最显著.而随着W逐渐增大,当对角无序强度还较弱时(如W=2)能带中心的奇异峰就会被完全地抑制掉,说明了对角无序起主导作用.因此,尽管1T-TaS2材料中存在由堆叠错位导致的非对角跃迁无序效应,但由于体系中不可避免地同时存在杂质和缺陷等引起的对角无序效应,因而实验中不容易观察到奇异峰的存在.此外,大家也会关心一个有趣的问题,在同时具有两种不同类型的无序体系中,奇异峰是随对角无序强度W的增加而逐渐消失还是发生突变呢?我们的研究发现这是一个渐变的过程,这将在后面的内容再做详细的讨论.

在一维体系中对角无序会使得所有的电子态均处于 Anderson局域态[16],而非对角跃迁无序的局域化效应仍然需要进行细致的理论研究.下面我们介绍一种判断是否发生Anderson局域化有效方法,即通过广义逆参与率 (general inverse participation ration,GIPR)[11]的晶格尺寸标度来完成.广义逆参与率GIPR是对逆参与率(IPR)的有效扩展,并与里亚诺夫指数等一起,为定量的研究有限尺寸的局域化问题提供了很好的理论支持.广义逆参与率GIPR的定义如下：

其中,ρ(ri,ω)是实空间格点上的局域态密度,它由格林函数的虚部来确定满足关系I2(N,ω)∝1/N.

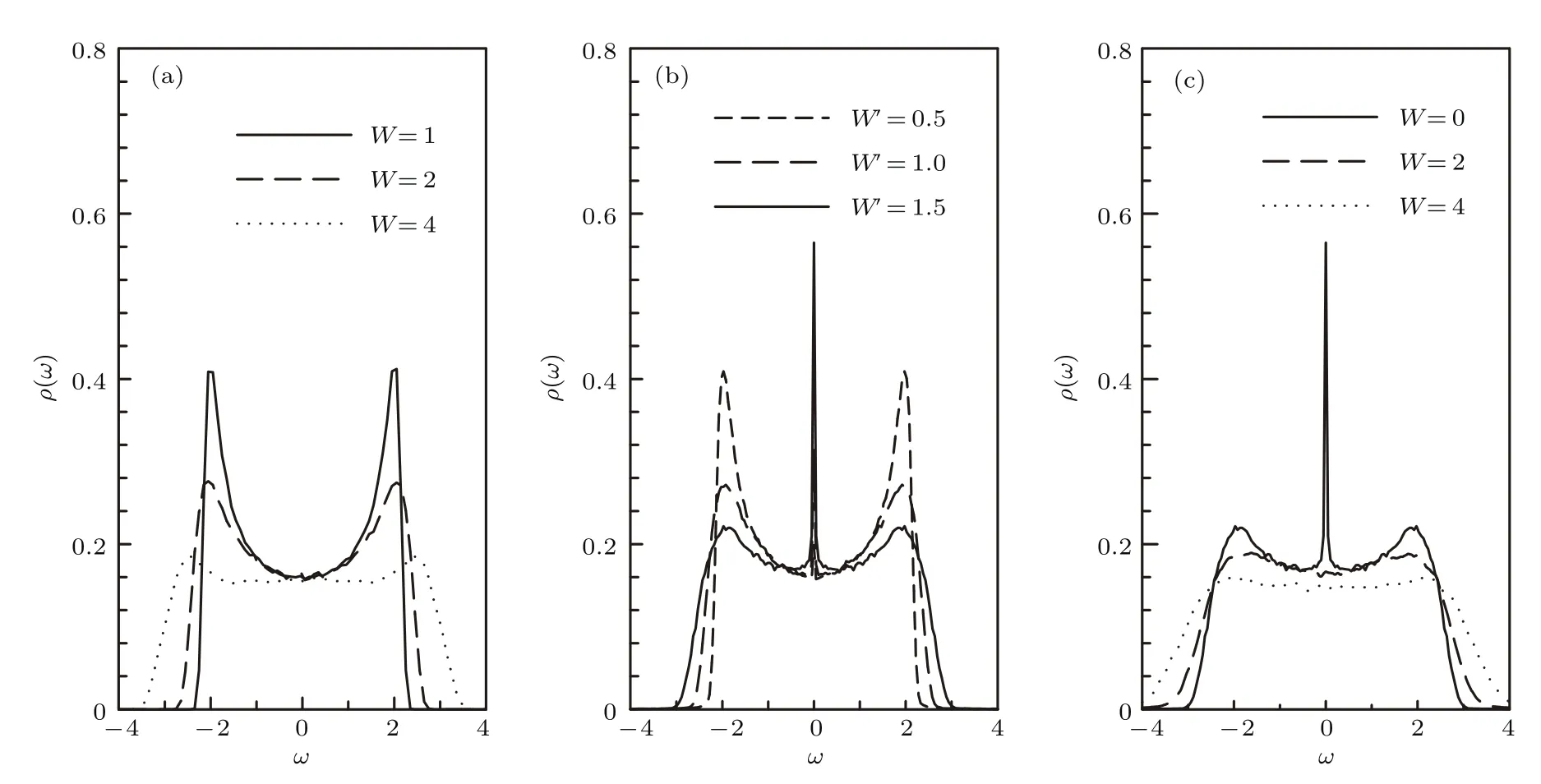
图1 两种不同类型的无序效应对无关联体系(U=0)态密度的影响 (a)当只考虑杂质所引入的对角无序效应时,体系的能带宽度会随着无序强度W 的增强而显著展宽;(b)堆叠错位引入的非对角无序的单独影响:随着无序强度W′的不断增大,体系的能带不仅有一定的拓宽,而且在能带中心ω=0处出现了一个奇异峰;(c)对角无序和非对角无序的共同效应:在非对角无序非常强时,即W′=1.5,较弱的对角无序效应 (W=2)就能够完全抑制态密度的奇异峰,这说明对角无序起着主导性作用;模型的主要计算参数取值:链长L=400—800,无序样本数Ns=100—300Fig.1.Effects of two different kinds of disorder on density of states(DOS)when U=0:(a)Energy band broadening with the increase of the disorder strength W when W′=0;(b)increasing of the anomalistic peak at the center of DOS with the increasing disorder strength W′when W=0;(c)the cooperative effect of the two different kinds of disorder,no anomalistic state can be found when W>1.0 and W′=1.5.Some other model parameters:The lattice size L=400–800 and the number of disordered configurations Ns=100–300.

图2 在无相互作用体系的能带中心位置,由非对角跃迁无序所导致的奇异态 (a)态密度在能带中心附近的局部放大图,展示了能带中心奇异峰随无序强度W′的增加而显著升高;(b)针对不同的无序强度W′取值,通过对能带中心尖峰态的逆参与率GIPR的晶格尺寸标度,证明了奇异态是Anderson局域的;模型计算参数与图1一致.Fig.2.Anomalistic states at the Fermi level introduced by the o ff-diagonal disorder:(a)The local ampli fication of the DOS around the Fermi level for the cases with different disorder strength W′;(b)the lattice sizes scaling of GIPR for different values of W′,and the anomalistic state at the center of the energy band is Anderson localized.

判定电子态是否为局域态的依据是看GIPR无穷极限的截距I2(∞,ω)是否为零,即

进而,还可以很方便地得到局域化长度ξloc

我们重点研究了奇异态的局域化问题,通过对其广义逆参与率 GIPR进行了晶格尺寸标度,得到了不同的无序强度W′下的局域化长度.如图2(a)所示,非对角跃迁无序强度的改变只对中心奇异峰有显著的影响,而周围的态密度基本不变.前面已经介绍过Thouless的理论[21],由于态密度与局域化长度的大小有密切的关联,我们的计算结果说明了只有奇异态的局域化长度会发生显著改变.如图2(b)所示.为了让标度结果更为准确,我们还结合了核多项式技术手段[22,23],补充了大晶格尺寸下的广义逆参与率GIPR的数值计算结果,而对于尺寸较小的晶体体系,我们的严格对角化方法和核多项式方法得到的结果是完全一致的.从图2(b)中可以看到GIPR与格点数的倒数1/N满足线性关系,并且在扩展到无穷极限 1/N→0得到有限的截距,说明奇异态是Anderson局域化的.当非对角无序强度分别为W′=0.5,W′=1.0,和W′=1.5时,所对应的截距分别为:I=8.38×10−5,I=1.63×10−4,和I=2.06×10−4,代入(9)式可得到相应的局域化长度:ξ=109.24,ξ=78.33,和ξ=69.67.正如预期,随着非对角跃迁无序强度的增强,能带中心奇异态的局域化不断增强,所对应的态密度奇异峰峰高也会显著提升.

在没有相互作用情况下,通过观察态密度的演化和广义逆参与率GIPR的晶格尺寸标度研究,发现不论是对角无序效应还是非对角跃迁无序都会导致体系中的所有电子态均发生Anderson局域化,特别是非对角跃迁无序导致能带中心出现一个奇异态,其局域化程度会随着无序强度的W′的增加而显著加强,使得态密度在能带中心位置出现尖锐的奇异峰.此外,由于体系中没有扩展态的存在,因而1T-TaS2材料在低温时只能是Anderson绝缘体,不会发生由无序效应导致的绝缘体到金属的相变.在下一节,我们进一步讨论电子关联效应对Anderson局域态的影响.

4.2 关联体系中的无序效应

由于非对角跃迁无序效应会导致无相互作用体系在能带中心出现一个反常的奇异态,为了探寻电子间的相互作用如何来影响这个奇异态,我们首先来研究同时具有电子关联和非对角跃迁无序效应的体系.对于半满体系,关联效应会在费米面处打开一个Mott能隙,从而产生出上下两个Hubbard子带.当体系中存在关联效应和非对角跃迁无序效应的共同影响时,我们发现体系中仍然会出现奇异态.如图3所示的态密度中存在奇异的尖峰,但与无相互作用体系单奇异峰结果不同,这时会出现两个等高的奇异峰,并分别位于上下Hubbard子带中相互对称的位置上.我们先来观察图3(a),当关联固定为U=2时,随着对角跃迁无序强度从W′=0.5增加到W′=1.5,两个奇异峰的位置均没有任何的改变,而峰高却显著升高,预示了奇异态的局域化随W′增大而增强,这与没有电子关联情况下得到的结果相一致.因此奇异峰的高度仍然是由无序强度来决定,而其位置则与电子关联的大小有密切的联系.

为了弄清楚奇异峰的位置与电子间相互作用U之间的具体关系,我们需要固定无序强度 (选取W′=1.5)来观察电子关联的单独影响,所得到的结果展示于图3(b).电子关联U的增强会导致Mott能隙的不断增大,而相应地,态密度中的奇异峰也随之向高能量区域移动.严格来看,两个奇异峰并不位于上下Hubbard子带的中心位置,而是分别处于ω=±U/2,两峰的间距正好是U.这预示了正是电子关联直接导致奇异态也发生了分离,这类似于在原子极限情况下(U/t→∞)Hubbard能级的劈裂,即电子关联使得上下Hubbard能级间隔刚好为U.而这里上下Hubbard子带中的两个对称的奇异态间距也刚好为U.本文只关注半满情况,而对于非半满体系中奇异态如何随关联而变化,我们将在今后的研究工作中进行讨论.

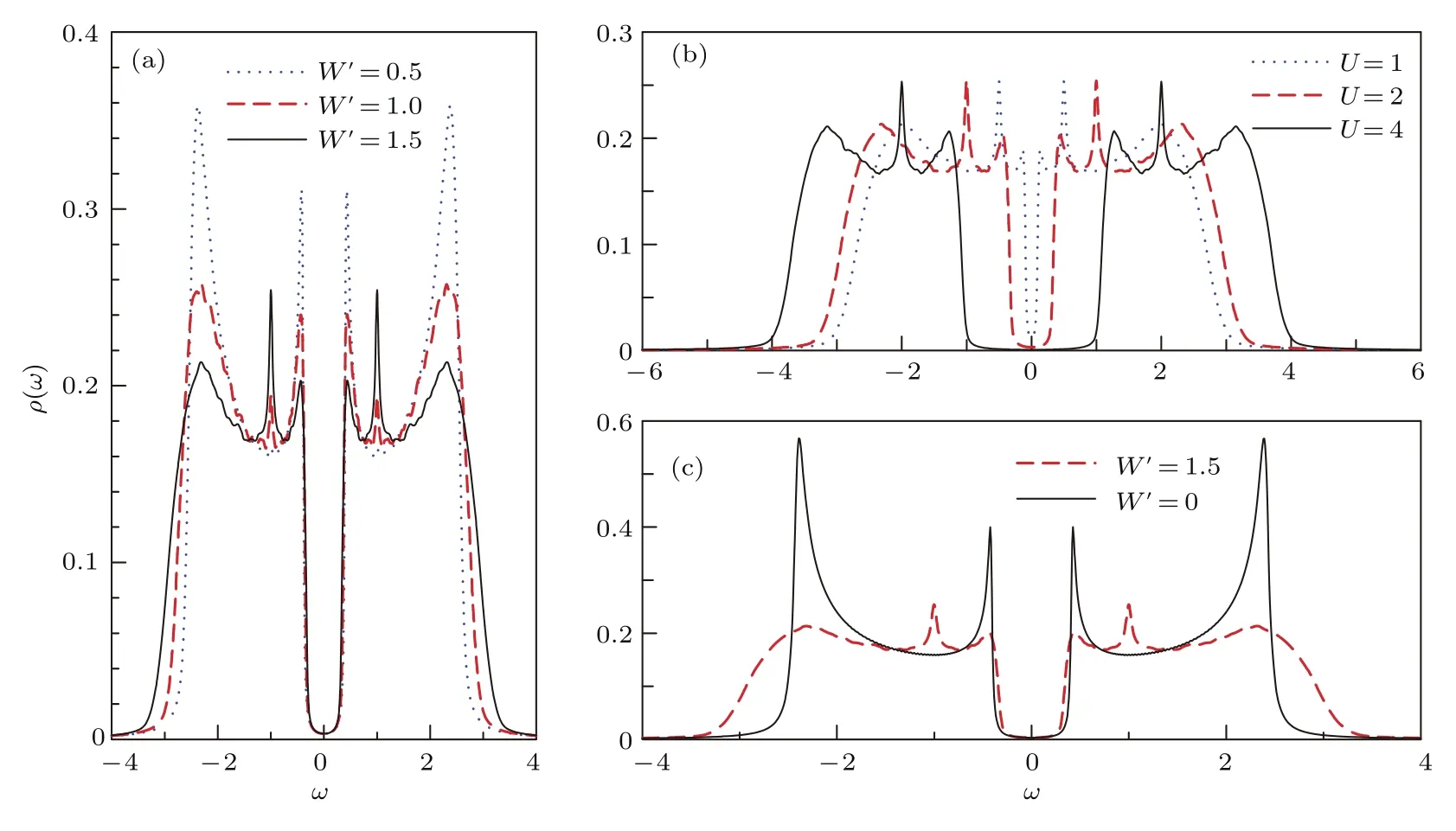
图3 (网刊彩色)非对角跃迁无序对关联体系态密度的作用和影响 (a)当相互作用U=2时,非对角跃迁无序导致上下Hubbard子带出现对称的奇异态,并位于ω=±1;(b)当非对角跃迁无序强度固定为W′=1.5,Mott能隙随U的增加而变大,同时,奇异峰的位置也随之向外移动,而峰高不随U改变;(c)关联体系的态密度在有无序和没有无序情况的比较,尽管非对角无序能够使Mott能隙变窄,但作用非常有限,完全不可能关闭Mott能隙;其他模型计算参数:晶格格点数为N=360,无序样本数为Ns=240Fig.3.(color online)The influence on DOS of the correlated systems with the hopping disorder:(a)Two anomalistic peaks are observed in lower and upper Hubbard subbands at ω = ±1 respectively,introduced by the hopping disorder when U=2;(b)the increase of Mott gap with the increasing U when W′=1.5,leading the anomalistic peaks move to the higher energy region;(c)comparison of the DOS of disordered and pure correlated systems with U=2.The other parameters are N=360 and Ns=240.

非对角跃迁无序效应无法关闭Mott能隙,这是我们获得的另一个重要结果.如图3所示,尽管非对角跃迁无序在上下Hubbard子带ω=U/2位置处产生出对称的奇异态,且态密度中奇异峰的高度会随着无序强度的增强而增大,但是Mott能隙的宽度并没有显著的改变.为了更清楚地表现Mott能隙的变化,我们将没有无序(W′=0)和有强非对角跃迁无序效应(W′=1.5)两种情况的态密度的对比展示于图3(c)中.显然非对角跃迁无序对Mott能隙的影响非常有限,当W′=1.5时能隙只是很有限地缩小,变化幅度小于10%,而这时的非对角跃迁无序强度已接近最大极限.因此在1T-TaS2材料中,单靠层间堆叠无序效应无法关闭Mott能隙,也就不会出现所谓的由层间堆叠无序效应诱导的绝缘体-金属转变,而材料中Mott绝缘机制始终占有主导地位.

在存在电子关联的体系中，非对角跃迁无序在上下Hubbard子带中所产生的奇异态是否有可能会变成扩展态,这也是一个非常重要的问题,需要进一步的理论研究.因此我们对奇异态的GIPR进行了晶格尺寸标度,并同时对上Hubbard子带中其他不同能量取值的准粒子态也进行了GIPR标度,结果如图4所示.我们发现当U=2时,奇异态的局域化长度为ξ=57.93,比没有相互作用情况的ξ=69.67取值更小,因此说明奇异态不会因相互作用的影响而变为扩展态.此外,其他不同能量的GIPR均呈现出有关晶格尺寸倒数(1/N)很好的线性关系,并且对无穷大晶格极限的延长结果都得到了有限的截距,因此说明所有的准粒子态都是Anderson局域态.

图4 (网刊彩色)在具有特定非对角跃迁无序强度的关联体系中不同能量电子态的广义逆参与率GIPR的晶格尺寸标度 内插图是标度直线延拓至无穷极限附近的局域放大图;随着能量ω的增加,准粒子态的Anderson局域性会逐步增强,而子带中的奇异态的局域性却会异常波动;模型参数为U=2和W′=1.5Fig.4.(color online)Lattice-size scaling of GIPR for the correlated systems with the hopping disorder.Inset:enlargement of the scaling lines of GIPR near the limitation of N→∞.The localization of the electronic states is enhanced with the increasing energy,except for the anomalistic state at ω=1.0.The model parameters are U=2 and W′=1.5.

图5 (网刊彩色)关联体系中对角无序和非对角跃迁无序的共同效应 (a)当非对角跃迁无序强度不变时(W′=1.5),通过增强对角无序强度能够完全关闭 Mott能隙;(b)当对角无序强度不变时 (W=1.0),通过增加非对角跃迁无序强度并不能改变Mott能隙的大小;(c)当非对角跃迁无序强度不变(W′=1.5)且对角无序强度较弱时,奇异峰会随W 的增强而逐渐被抑制并最终完全消失;模型计算参数:U=2,L=360和Ns=100—300Fig.5.(color online)Cooperative effect of the diagonal and o ff-diagonal disorder on DOS:(a)Mott gap can be completely closed with the increasing W when the hopping disorder strength is very large as W′=1.5;(b)no manifest change of Mott gap can be observed with the increasing W′when W=1.0;(c)the suppression on the anomalistic peak in DOS by the diagonal disorder.Model parameters:U=2,L=360 and Ns=100–300.

为了更清晰地呈现标度结果,我们在内插图中对于接近无穷极限部分进行了放大,除了ω=1(U=2)的奇异态以外,随着能量的升高截距也不断增大,预示了局域化程度的增加.而奇异态的标度结果出现反常,即奇异态的GIPR标度截距较其他任何态的截距取值更小,预示了奇异态的局域化长度更大.这表明有相互作用体系中奇异态的特性与无相互作用体系中奇异态的特性很相似.在上一节中我们已经介绍到早期的理论研究发现[17],无相互作用体系中奇异态的局域化长度是发散的,因此推断奇异态是扩展态.之后更精确的计算证明了奇异态实际是一种特殊的局域态[19],并且奇异态的局域化长度较一般态的局域化长度要大很多.而在有相互作用的情况下我们也得到了类似的结论.

最后来讨论在关联体系中对角无序和非对角跃迁无序的共同效应.如图5所示,当进一步引入对角跃迁无序的影响后,随着无序强度W的增强不仅态密度中的奇异峰会逐渐消失,而且Mott能隙也逐渐减小直至完全消失.图5(a)展示的是在U=2和W′=1.5时,态密度随W的变化.随着W的增加,Mott能隙会显著变窄,并很快演变成为一个赝能隙.当无序强度增大到一定程度(W>U),Mott能隙完全闭合.需要强调的是,没有Mott能隙并不意味着体系变成了金属态,标度理论告诉我们体系中的无序效应导致了所有的准粒子态都是Anderson局域态.此外,图5(c)展示了奇异峰的消失是一个渐变的过程,当对角无序强度较弱时(W=0.25),仍然能够看到奇异峰的存在,但峰高降低超过一半.因而只有在相较而言非对角跃迁无序比对角无序大很多时,即W′/W>5,才有可能实验观察到奇异峰的存在.因而目前实验还无法观测到这个奇异态,最可能的原因是体系中杂质引入的无序强度W相对较强,这有待实验研究的进一步证实.

第一性原理计算认为[24],1T-TaS2的CCDW相是一维金属相,而非半导体或绝缘相,但实验研究却证明了 CCDW 相是绝缘相[6],理论计算的结果与实验发现相矛盾.而我们的理论研究表明,不论材料中关联占主导还是无序占主导,都不会出现金属相,更不会发生由无序诱导的绝缘体-金属相变.因此我们的理论研究能够更加合理地解释1T-TaS2体材料有关CCDW 相的实验结果.

5 结 论

本文所采用的统计动力学平均场理论数值方法能够合理地研究关联体系中的无序效应.针对半满的1T-TaS2体材料,研究了层间堆叠错位和杂质引入的无序效应与电子关联的竞争和共同影响.尽管对角无序效应能够完全关闭Mott能隙,但扩展的逆参与率晶格尺寸标度研究证明了所有的准粒子态都是Anderson局域态,因此不会发生由无序诱导的从绝缘体到金属的转变.而非对角跃迁无序效应能够在态密度中引入一个奇异峰,并在电子关联的作用下分裂为两个对称的峰,分别位于上下Hubbard子带中,而且这个奇异态仍然是Anderson局域态.

[1]Phillips P 2010Rev.Mod.Phys.82 1719

[2]Lee P A,Ramekrishnan T V 1985Rev.Mod.Phys.57 287

[3]Abrahams E 201050 Years of Anderson Localization(Singapore:World Scientific Publishing)

[4]Lahoud E,Meetei O N,Chaska K B,Kanigel A,Trivedi N 2014Phys.Rev.Lett.112 206402

[5]Fazekas P,Tosatti E 1980Physica B99 183

[6]Sato H,Arita M,Utsumi Y,Mukaegawa Y,Sasaki M,Ohnishi A,Kitaura M,Namatame H,Taniguchi M 2014Phys.Rev.B89 155137

[7]Bayliss S C,Clark A,Liang W Y 1983J.Phys.C:Solid State Phys.16 L831

[8]Wilson J A,Di Salvo F J,Mahajan S 2001Adv.Phys.50 1171

[9]Wilson J A,Di Salvo F J,Mahajan S 1975Adv.Phys.24 117

[10]Fung K,Steeds J,Eades J 1980Physica B+C99 47

[11]Song Y,Wortis R,Atkinson W A 2008Phys.Rev.B77 054202

[12]Claessen R,Burandt B,Carstensen H,Skibowski M 1990Phys.Rev.B41 8270

[13]Rossnagel K,Smith N V 2006Phys.Rev.B73 073106

[14]Smith N V,Kevan S D,DiSalvo F J 1985J.Phys.C:Solid State Phys.18 3175

[15]Georges A,Kotliar G,Krauth W,Rozenberg M J 1996Rev.Mod.Phys.68 13

[16]Song Y,Atkinson W A,Wortis R 2007Phys.Rev.B76 045105

[17]Theodorou G,Cohen M H 1976Phys.Rev.B13 4597

[18]Eggarter T P,Riedinger R 1978Phys.Rev.B18 569

[19]Fleishman L,Licciardello D C 1977J.Phys.C:Solid State Phys.10 L125

[20]Soukoulis C M,Economou E N 1981Phys.Rev.B24 5698

[21]Thouless D J 1972J.Phys.C5 77

[22]Sun J,He L,Zhao Y Y,Song Y 2016Sci.China:Phys.Mech.Astron.59 617401

[23]He L,Song Y 2013Acta Phys.Sin.62 057303(in Chinese)[何龙,宋筠 2013物理学报 62 057303]

[24]Lazar P,Martincova J,Otyepka M 2015Phys.Rev.B92 224104

PACS:71.10.–w,74.62.En,71.27.+a,71.30.+h DOI:10.7498/aps.66.057101

Anderson localization effect on Mott phase in 1T-TaS2∗

Zhao Yang-Yang Song Yun†
(Department of Physics,Beijing Normal University,Beijing 100875,China)

24 October 2016;revised manuscript

21 November 2016)

In the layered dichalcogenide 1T-TaS2,whether there is a disorder-driven transition from insulator to metal is still a matter in dispute.It is predicted that the commensurate charge density wave(CCDW)phase at low temperature behaves as a Mott insulator due to the strong correlation of electrons.Meanwhile,the stacking of TaS layers is found to be dislocated along thecaxis,which will introduce considerable effect of disorder.Therefore,further theoretical study is needed to show the cooperative effect of correlation and disorder in 1T-TaS2.

The statistical dynamical mean-field theory,which treats interactions and disorder on an equal footing,is used to study the effect of disorder on the Mott insulating phase in 1T-TaS2.Two different kinds of disorder effects are considered in the one-dimensional extended Anderson-Hubbard model,where the stacking dislocation of TaS layers is described by the o ff-diagonal hopping disorder and the diagonal disorder term represents the effect of disorder introduced by impurities.

We find that the o ff-diagonal disorder by itself could not close the Mott gap at Fermi level,suggesting that Mott mechanism should be more dominant in the CCDW phase of 1T-TaS2with the stacking dislocation of TaS layers.On the other hand,the diagonal disorder introduced by impurities will close the Mott gap when the strength of disorder(W)is larger than the correlation of electrons(U).Proved by the lattice-size scaling of the generalized inverse participation ratio,both the o ff-diagonal disorder and diagonal disorder can make all states Anderson-localized.As a result,there is no disorder-induced metal-insulator transition in a correlated system with either o ff-diagonal disorder or diagonal disorder.

In addition,an anomalistic state is introduced by the o ff-diagonal disorder at the center of the energy band of the non-interacting system,which is a special Anderson-localized state with a very larger localization length.In the correlated cases,the electron-electron interactions have strong effect on splitting the anomalistic state into two individual states,which are located symmetrically in both the upper and lower Hubbard subbands with an energy intervalU.

dynamical mean-field theory,Mott insulating phase,Anderson localization,o ff-diagonal disorder

PACS:71.10.–w,74.62.En,71.27.+a,71.30.+h

10.7498/aps.66.057101

∗国家自然科学基金(批准号:11174036,11474023)、国家重点基础研究发展计划(批准号:2011CBA00108)和中央高校基本科研业务费资助的课题.

†通信作者.E-mail:yunsong@bnu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11174036,11474023),the National Basic Research Program of China(Grant No.2011CBA00108),and the Fundamental Research Funds for the Central Universities,China.

†Corresponding author.E-mail:yunsong@bnu.edu.cn