竞争非局域三次五次非线性介质中孤子的传输特性∗

黄光侨 林机

(浙江师范大学物理系,金华 321004)

竞争非局域三次五次非线性介质中孤子的传输特性∗

黄光侨 林机†

(浙江师范大学物理系,金华 321004)

(2016年9月11日收到;2016年12月5日收到修改稿)

研究空间光孤子在一维竞争非局域三次五次非线性介质中的新解和传输特性.发现亮孤子在竞争非局域三次自散焦和五次自聚焦非线性介质中存在不稳定区间.在一般非局域程度下,对于不同的三次非线性效应,同相位复合两孤子间表现为吸引或排斥的相互作用,并讨论了折射率的变化.在竞争非局域三次自聚焦和五次自散焦非线性介质中给出了二极、三极和四极孤子能稳定传播的条件,研究发现更高极孤子的传播是不稳定的.还研究了孤子功率与传播常数以及非局域程度的关系.

非局域非线性效应,空间光孤子,稳定性

1 引 言

空间光孤子是线性衍射效应与非线性效应共同作用并精确平衡的结果.材料的非线性空间非局域性是指材料中空间某点的非线性折射率不仅与该点的光场有关,还与该点附近一个区域内的光场有关. 孤子在向列液晶[1−4]、铅玻璃[5−8]、热致非线性材料[9]和偶极玻色爱因斯坦凝聚体[10]等材料中表现出非局域非线性物理特性.其中,在向列液晶的非局域介质中亮孤子的吸引和排斥相互作用的临界值[11],暗孤子长程相互作用产生的稳定束缚态[12],非局域亮孤子在竞争自聚焦和自散焦非线性介质中的相互作用[13],这些特性都表明不同非局域非线性响应对研究空间光孤子的传输动力学有重要作用.此外,在非局域非线性克尔介质中,利用李群约化方法给出多种类型光孤子的解析解和Airy数值行波解[14],扩展了Snyder和Mitchell模型的理论分析[15].与Snyder和Mitchell的一维非局域模型相比,Mihalache等[16]在2006年提出的一维竞争非局域三次五次非线性模型,研究了竞争非局域自聚焦三次和自散焦五次非线性介质中亮孤子和偶极孤子的传输稳定性,并且证明了基本孤子的稳定性严格遵循Vakhitov-Kolokolov定则.Doktorov和Molchan[17]根据Toda链模型给出弱非局域三次五次介质中多孤子(链孤子)的解析解,并用数值分析孤子与孤子之间的相互补偿作用.对于弱非局域三次五次介质,Tosy[18]研究了亮孤子和暗孤子的特点.Zhou等[19]研究了非局域三次五次介质中受到自聚焦和自散焦非线性干扰的暗孤子的特点及其传输碰撞的动力学行为.此外,大量研究报道了非局域非线性介质中的多极孤子.在非局域克尔介质中,Xu等[20]发现偶极、三极和四极孤子可以稳定传输,但更高阶孤子的束缚态则不稳定.Dong等[21]发现在一维热非线性介质中,三极和四极孤子可在有限非局域范围内稳定传输.

非局域非线性三次自散焦和五次自聚焦介质中的亮孤子和多极孤子以及三次自聚焦和五次自散焦非线性介质中的多极孤子方面的报道较少.本文主要分析非局域非线性三次自散焦和五次自聚焦介质中亮孤子的特点,以及非局域非线性程度对同相位两孤子之间排斥或吸引等相互作用的影响.研究多极孤子在非局域三次自聚焦和五次自散焦非线性介质中的传输稳定性.

2 非局域亮孤子解及其传输的稳定性

由Mihalache提出的一维竞争非局域三次五次非线性模型可由非局域非线性薛定谔方程描述为

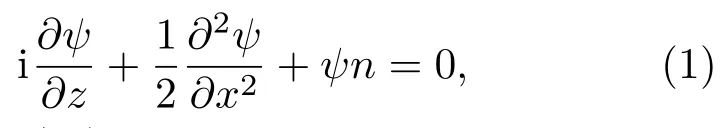
式中ψ为光场振幅,x和z分别为横坐标上的光束宽度和纵向坐标上的衍射长度,n为诱导折射率.(1)式中非线性项对应光场的诱导折射率为

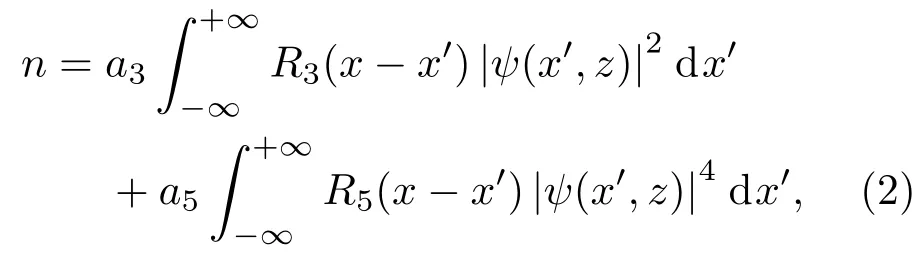
图1 (网刊彩色)基本孤子的功率和传播性质 (a)d3=d5=0时功率与传播常数的关系;(b)d5=10时功率与传播常数的关系;(c)b=1时孤子的光场波形和诱导折射率;(d)b=0.4时的亮孤子传输图;(e)b=0.6时的亮孤子传输图Fig.1.(color online)Properties of the power and the propagation of the basic solitons:(a)The power versus the propagation constant when d3=d5=0;(b)the power versus the propagation constant when d5=10;(c)the structures of basic optical solitons and the induced refractive index when b=1;(d)propagation of the bright solitons when b=0.4;(e)propagation of the bright solitons when b=0.6.

设(1)式和(2)式中ψ(z,x)=w(x)exp(ibz),其中w为孤子振幅,b为孤子传播常数.为了研究非局域参数对孤子传播的影响,预先假定三次自散焦和五次自聚焦的非线性参数分别为a3=−1,a5=2,运用数值计算方法获得不同非局域参数d3和d5下该模型亮孤子(选取高斯型)的功率和传输稳定性,如图1所示.图1(a)为局域介质即非局域程度d3=d5=0时的功率曲线,亮孤子功率随传播常数b始终是单调递减的,存在最大功率值Umax=2.6.它与文献[16]中三次自聚焦和五次自散焦非线性介质中局域亮孤子的功率曲线情况相反,因此,这种局域非线性介质不存在稳定亮孤子.但是研究发现,对于非局域三次自散焦和五次自聚焦非线性介质,亮孤子存在一小段不稳定区间.当非局域程度不同时,孤子功率随传播常数先单调递减后单调递增,存在一个功率最小值Umin.图1(b)为d5=10而d3取不同值时亮孤子功率随传播常数b的变化曲线.当非局域参数d3=0.3时,传播常数b=0.259,孤子最小功率Umin=8.755;当d3=3时,传播常数b=0.463,孤子最小功率Umin=5.972;当d3=10时,传播常数b=0.117,孤子最小功率Umin=4.393.在dU/db>0区间内存在稳定亮孤子,否则亮孤子不稳定.从图1(d)可以看出,dU/db<0时,非线性效应较弱,孤子在传输过程中发散,而从图1(e)可以看出,dU/db>0时,衍射效应和非线性效应平衡后亮孤子传输稳定性很好.此外,还研究了亮孤子束宽和振幅与非局域程度的关系.从图1(c)可知,非局域参数d5不变时,随着非局域参数d3的增加,亮孤子束宽变窄,振幅值变大.在三次自散焦非线性介质中,孤子的诱导折射率波峰向上凸起,这不利于多峰孤子之间的传输稳定性.

3 同相位复合两孤子相互作用的数值分析

图2 (网刊彩色)不同非线性参量下同相位两孤子的相互作用 (a)a3=−0.1,两孤子间距L=12.876时孤子的光场波形和诱导折射率;(b)a3=−1.69,L=4.878时孤子的光场波形和诱导折射率;(c)a3=−1.73,L=4.822时孤子的光场波形和诱导折射率;(d)a3=−0.1,L=12.876时的孤子传输图;(e)a3=−1.69,L=4.878时的孤子传输图;(f)a3=−1.73,L=4.822时的孤子传输图Fig.2.(color online)The interaction of the two solitons with the same phase for different nonlinear parameters:(a)Soliton structure and induced refractive index when a3=−0.1 and the interval of two solitons L is 12.876;(b)soliton structure and induced refractive index when a3=−1.69 and L=4.878;(c)soliton structure and induced refractive index when a3= −1.73 and L=4.822;(d)propagation when a3= −0.1 and L=12.876;(e)propagation when a3=−1.69 and L=4.878;(f)propagation when a3=−1.73 and L=4.822.

本节分别研究非局域参数不变时改变非线性参数和非线性参数不变时改变非局域参数对同相位复合两孤子的传播特性的影响.首先,在竞争非局域三次自散焦和五次自聚焦非线性介质中,假定传播常数b=1,五次非线性参数a5=2,非局域参数d3=2,d5=1,此时复合同相位两孤子的相互作用特点如图2所示.当自散焦a3很弱时(图2(a)),诱导折射率并没有负的尾部,而且中心位置光场强度为零,引起了排斥作用力,使非线性效应和衍射效应完全平衡,两个同相位孤子稳定传输(图2(d)).当非局域参数d3>d5时,三次五次非线性响应函数具有负的尾部,相应的诱导折射率两侧分布出现了负区间(图2).从图2(b)和图2(c)可以发现,诱导折射率的中间凹点离x轴的原点都有一定的距离,这将影响两孤子传输的稳定性.当自散焦参数a3达到一个临界值时,由于自散焦效应,孤子与孤子之间最后会快速分裂排斥传输.从图2(c)可以观察到当a3达到临界值时孤子开始分裂,其中的一个孤峰振幅值比另一个孤峰振幅值大.在数值结果中出现两孤子吸引和分裂的纠缠状态下其中一个孤峰会因为自散焦作用发散湮没.当非局域效应较强时,两孤子会被吸引到一起合并成一个孤子(图2(e)),与文献[22]中基本孤子再次出现相互吸引和排斥的交叠状态传输现象不同.当a3减小时两孤子间距反而增大.对于d5>d3情形,文献[23]研究表明三次五次非线性响应函数具有负的尾部,而相应的诱导折射率变化也在两孤子接近x轴尾端为负.

其次,我们研究了非局域程度对两孤子传播的影响.假定三次非线性参数a3=−1,其他参数同上,运用数值模拟得到不同非局域参数d3条件下同相位两孤子相互作用的传播特点,如图3所示.当衍射效应和非线性效应达到平衡时,同相位的两个孤子可以稳定地传输(图3(d)).研究还发现随着非局域参数d3的增大,两孤子间距虽然减小,但是两孤子的相互作用由排斥转为吸引.这是因为孤子与孤子的中心光场为零,孤子之间总是排斥.当较弱的非局域响应诱导孤子间的吸引作用比排斥作用小时,两孤子就进行排斥传输(图3(e));反之,两孤子相互吸引,融合在一起(图3(f)).

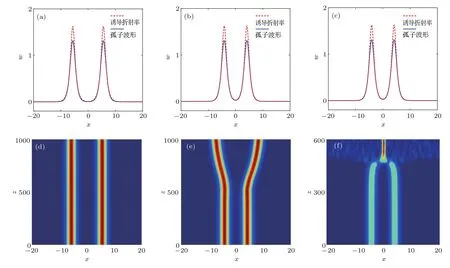
图3 (网刊彩色)不同非局域程度下同相位两孤子的相互作用 (a)d3=1.2,L=11.236时孤子的光场波形和诱导折射率;(b)d3=1.38,L=8.308时孤子的光场波形和诱导折射率;(c)d3=1.39,L=8.220时孤子的光场波形和诱导折射率;(d)d3=1.2,L=11.236时的传输图;(e)d3=1.38,L=8.308时的传输图;(f)d3=1.39,L=8.220时的传输图Fig.3.(color online)The interaction of two optical solitons with the same phase for different nonlocal parameters:(a)Soliton structure and induced refractive index when d3=1.2 and L=11.236;(b)soliton structure and induced refractive index when d3=1.38 and L=8.308;(c)soliton structure and induced refractive index when d3=1.39 and L=8.220;(d)propagation when d3=1.2 and L=11.236;(e)propagation when d3=1.38 and L=8.308;(f)propagation when d3=1.39 and L=8.220.

图4 两孤子在自散焦介质中的功率曲线 (a)U-b曲线;(b)U-d3曲线Fig.4.The power curves of the two solitons in the self-defocusing medium:(a)U-b curves;(b)U-d3curves.

同时,我们还研究了两孤子的功率与传播常数之间的关系.在图4(a)中,同相位两孤子的功率随着传播常数的变化会因为三次自散焦非线性参数的不同而不同.a3=−0.1时,b<0.39的区间内不存在两孤子解;当传播常数b大于该值时,功率值开始单调递增,这与a3=−1或−2时孤子功率都有先单调递减再递增的变化过程不同.a3=−1或−2时,两孤子都存在最小功率值Umin,分别为5.305和6.658.当功率高于此临界值时,随着传播常数的增加,孤子间距变窄而振幅值变大.从图4(b)可发现,在相对弱非线性a3=−0.1条件下,U−d3曲线基本上与x轴平行,这时自散焦作用影响很弱,容易出现稳定传输的同相位两孤子.而在其他非线性a3参数下,功率U都是随着d3单调递减.

我们还对三极孤子、四极孤子和五极孤子的传播稳定性进行了数值计算,发现在一定的参数条件下孤子能稳定传输,但是对六极孤子及以上的孤子没有找到合适的参数使其稳定传播.

4 竞争非局域多极孤子的传输特性

为了研究竞争非局域三次五次非线性介质中多极孤子的传输稳定性,将(1)式和(2)式的初始输入加白噪声ψ(x,z=0)=w(x)[1+ρ(x)],其中ρ(x)为高斯分布的随机噪声且方差δ2=0.01.将以上初始条件代入(1)式和(2)式,并利用分步傅里叶方法进行数值模拟得到白噪声扰动下的多极孤子传输图像.以下主要讨论在竞争非局域三次自聚焦和五次自散焦非线性介质中的多极孤子的特点及其传输特性.

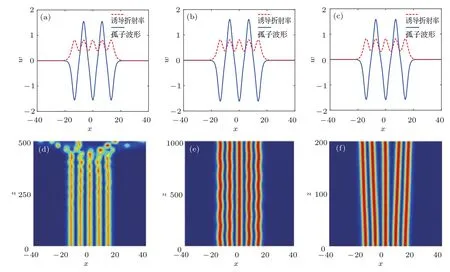
由三个不同相位的孤子组成的三极孤子(也称为束缚态)在竞争非局域三次五次非线性介质中可以稳定传输.不同非局域程度下三极孤子的特点和传输特性如图5所示.给定传播常数b=0.6、非线性参量a3=1,a5=−0.23和非局域参数d3=3,从图5(a)—(c)可以看出,随着非局域参数d5的增大,三极孤子光束束宽变窄,振幅值变小,功率也减小.相位相反的孤子之间存在排斥作用,所以当非局域参数d5小于某一个阈值时,三极孤子的两侧孤子无法被排斥传输,而是出现振荡传输,并且融合后能分裂出两个孤峰(图5(d)).当非局域参数4

四极孤子由两两反相孤子所构成,所以它们之间既有排斥作用,又有相互吸引作用.图7为不同非局域程度下四极孤子的特点和传输特性.给定b=0.6,a3=1,d3=3,d5=5,减小五次非线性参量a5值时,孤子之间的吸引作用增强,同时孤子的振幅值也相应增大;反之,孤子排斥作用增大,幅值减小.仅在a5=−0.23处吸引作用和排斥作用相互平衡,出现稳定传输的四极孤子(图7(e)),在自散焦非线性a5<−0.24区域内不存在四极孤子的数值解.随着五次非局域程度的变化,四极孤子比三极孤子稳定性更差.在数值模拟中发现四极孤子在4

图5 (网刊彩色)不同非局域程度下三极孤子的特点和传输特性 (a)d5=1时孤子的光场波形和诱导折射率;(b)d5=5时孤子的光场波形和诱导折射率;(c)d5=8时孤子的光场波形和诱导折射率;(d)d5=1时加δ2=0.01白噪声的传输图;(e)d5=5时加δ2=0.01白噪声的传输图;(f)d5=8时加δ2=0.01白噪声的传输图Fig.5.(color online)The characteristics and the propagation properties of the triple-pole solitons for different nonlocal parameters:(a)Soliton structure and induced refractive index when d5=1;(b)soliton structure and induced refractive index when d5=5;(c)soliton structure and induced refractive index when d5=8;(d)propagation with the white noise of δ2=0.01 when d5=1;(e)propagation with the white noise of δ2=0.01 when d5=5;(f)propagation with the white noise of δ2=0.01 when d5=8.

由以上的数值结果分析可得,参数b=0.6,a3=1,a5=−0.23,d3=3,d5=5时也可能会出现稳定的五极孤子.然而,图8(d)中的数值模拟结果表明在该参数条件下不存在稳定传输的五极孤子.为了找出传输更加稳定的五极孤子,尝试增加五次非线性参量a5=−0.24.由图8(e)发现五极孤子加白噪声情况下,除中间孤子外其他孤子都呈波浪式不稳定传输.与a5=−0.23时的传输相比,该非局域程度的五极孤子传输更加稳定,也说明前者五个孤子之间的排斥作用较弱,不足以使五极孤子稳定传输.随着非局域参数d5的减小,五极孤子传输已经变得没有规则,随时有坍塌现象发生.而在d5>6的情况下,孤子与孤子的排斥作用增强,五极孤子除中间的孤子外,其他四个孤子以最快的速度排斥传输.通过大量的数值计算发现,在其他参数不变情况下,只在d3

图6 (网刊彩色)不同非局域非线性下三极孤子的特点和传输特性 (a)a3=0.95,a5=−0.22,d3=d5=2时孤子的光场波形和诱导折射率结构图;(b)a3=1,a5=−0.2,d3=d5=8时孤子的光场波形和诱导折射率结构图;(c)a3=0.95,a5=−0.22,d3=d5=2时三极孤子加δ2=0.01白噪声的传输图;(d)a3=1,a5=−0.2,d3=d5=8时不加微扰的不稳定传输图Fig.6.(color online)The characteristics and the propagation properties of the triple-pole solitons for the different nonlocal nonlinear parameters:(a)Soliton structure and induced refractive index when a3=0.95,a5=−0.22,and d3=d5=2;(b)soliton structure and induced refractive index when a3=1,a5=−0.2,and d3=d5=8;(c)propagation of the triple-pole solitons with the white noise of δ2=0.01 when a3=0.95,a5= −0.22,and d3=d5=2;(e)propagation without white noise when a3=1,a5=−0.2,and d3=d5=8.

图7 (网刊彩色)不同非局域程度下四极孤子的特点和传输特性 (a)d5=3时孤子的光场波形和诱导折射率;(b)d5=5时孤子的光场波形和诱导折射率;(c)d5=8时孤子的光场波形和诱导折射率;(d)d5=3时加δ2=0.01白噪声的传输图;(e)d5=5时加δ2=0.01白噪声的传输图;(f)d5=8时加白噪声δ2=0.01的传输图Fig.7.(color online)The characteristics and the propagation properties of the quadrupole solitons for the different nonlocal parameters:(a)Soliton structure and induced refractive index when d5=3;(b)soliton structure and induced refractive index when d5=5;(c)soliton structure and induced refractive index when d5=8;(d)propagation with the white noise of δ2=0.01 when d5=3;(e)propagation with the white noise of δ2=0.01 when d5=5;(f)propagation with the white noise of δ2=0.01 when d5=8.

图8 (网刊彩色)不同非局域程度下五极孤子的特点和传输特性(a)a5=−0.23,d3=3,d5=5时孤子的光场波形和诱导折射率结构图;(b)a5=−0.24,d3=3,d5=5时孤子的光场波形和诱导折射率结构图;(c)a5=−0.24,d3=3,d5=6时孤子的光场波形和诱导折射率结构图;(d)a5=−0.23,d3=3,d5=5时加δ2=0.01白噪声的传输图;(e)a5=−0.24,d3=3,d5=5时加δ2=0.01白噪声的传输图;(f)a5=−0.24,d3=3,d5=6时加δ2=0.01白噪声的传输图Fig.8.(color online)The characteristics and the propagation properties of the penta-pole solitons for different nonlocalities:(a)Soliton structure and induced refractive index when a5=−0.23,d3=3,and d5=5;(b)soliton structure and induced refractive index when a5=−0.24,d3=3,and d5=5;(c)soliton structure and induced refractive index when a5=−0.24,d3=3,and d5=6;(d)propagation with the white noise of δ2=0.01 when a5= −0.23,d3=3,and d5=5;(e)propagation with the white noise of δ2=0.01 when a5= −0.24,d3=3,and d5=5;(f)propagation with the white noise of δ2=0.01 when a5=−0.24,d3=3,and d5=6.

5 结 论

运用数值计算方法研究了竞争非局域三次五次非线性介质中不同类型空间光孤子的存在和传播稳定性.在非局域三次自散焦和五次自聚焦的非线性介质中亮孤子的功率随传播常数的变化曲线并不是单调递增的,孤子存在不稳定区间.一般非局域程度下同相位复合的两孤子考虑不同的非线性效应时,其相互作用具有不同性质.此外,还给出了非局域非线性三次自聚焦和五次自散焦介质中的多极孤子稳定性条件,在满足一定的参数关系时,二极、三极和四极孤子能稳定传播,但不存在五极以上(包括五极)的稳定传播的孤子.对以上所有情形,都给出了折射率的数值计算结果.

[1]Conti C,Peccianti M,Assanto G 2003Phys.Rev.Lett.91 073901

[2]Conti C,Peccianti M,Assanto G 2004Phys.Rev.Lett.92 113902

[3]Fratalocchi A,Assanto G,Brzdakiewicz K A,Karpierz M A 2004Opt.Lett.29 1530

[4]Conti C,Peccianti M,Assanto G 2006Opt.Lett.31 2030

[5]Dabby F W,Whinnery J R 1968Appl.Phys.Lett.13 284

[6]Rotschild C,Cohen O,Manela O,Segev M,Carmon T 2005Phys.Rev.Lett.95 213904

[7]Xie Y Q,Guo Q 2004Acta Phys.Sin.53 3020(in Chinese)[谢逸群,郭旗 2004物理学报 53 3020]

[8]Cao J N,Guo Q 2005Acta Phys.Sin.54 3688(in Chinese)[曹觉能,郭旗 2005物理学报 54 3688]

[9]Ghofraniha N,Conti C,Ruocco G,Trillo S 2007Phys.Rev.Lett.99 043903

[10]Burger S,Bongs K,Dettmer S,Ertmer W,Sengstock K,Sanpera A,Shlyapnikov G V,Lewenstein M 1999Phys.Rev.Lett.83 5198

[11]Rasmussen P D,Bang O,Krolikowski W 2005Phys.Rev.E72 066611

[12]Nikolov N I,Neshev D,Krolikowski W,Bang O,Rasmussen J J,Christiansen P L 2004Opt.Lett.29 286

[13]Esbensen B K,Bache M,Bang O,Krolikowski W 2012Phys.Rev.A86 033838

[14]Jia J,Lin J 2012Opt.Express20 7469

[15]Snyder A W,Mitchell D J 1997Science276 1538

[16]Mihalache D,Mazilu D,Lederer F,Crasovan L C,Kartashov Y V,Torner L,Malomed B A 2006Phys.Rev.E74 066614

[17]Doktorov E V,Molchan M A 2008J.Phys.A:Math.Theor.41 315101

[18]Tsoy E N 2010Phys.Rev.A82 063829

[19]Zhou Z X,Du Y W,Hou C F,Tian H,Wang Y 2011J.Opt.Soc.Am.B28 1583

[20]Xu Z Y,Kartashov Y V,Torner L 2005Opt.Lett.30 3171

[21]Dong L W,Ye F W 2010Phys.Rev.A81 013815

[22]Kartashov Y V,Vysloukh V A,Torner L 2008Opt.Lett.33 1747

[23]Du Y W,Zhou Z X,Tian H,Liu D J 2011J.Opt.13 015201

PACS:42.70.Nq,42.65.Sf DOI:10.7498/aps.66.054208

Propagating properties of spatial solitons in the competing nonlocal cubic-quintic nonlinear media∗

Huang Guang-Qiao Lin Ji†

(Department of Physics,Zhejiang Normal University,Jinhua 321004,China)

11 September 2016;revised manuscript

5 December 2016)

We study the new spatial optical solitons and their propagating properties in the one-dimensional nonlocal cubicquintic(C-Q)nonlinear model by the numerical method.We obtain multi-bright solitons and multipole soliton solutions in the one-dimensional nonlocal C-Q nonlinear model.The propagation of bright solitons is stable in the competing nonlocal cubic self-defocusing and quintic self-focusing nonlinear media when these nonlocal and nonlinear parameters are in the appropriate value domain.Considering the different nonlinear cubic effects,the interaction between two optical solitons with the same phase in the general nonlocal media displays the attraction or the repulsion for different nonlocal and nonlinear parameters.We find that the interval of two solitons affects the interaction between them.The refractive index is changed with the propagating constant when the nonlocal constantd3is 10.Moreover,the triplepole,quadrupole and pentapole solitons can propagate steadily when the nonlocal parameters are appropriate,but hexa-pole(or above)solitons propagate unsteadily for any nonlocal parameter.Furthermore,we investigate the multi-pole solitons and their propagation stabilities by the Newton difference method and the Fourier split step method,obtain the stable propagation conditions for dipole,triplepole and quadrupole solitons,and find that the propagation of the pentapole and higher-order pole solitons is unstable.We also discuss the interactions of multi-pole solitons when they propagate along the axisz.The interactions are attraction or repulsion when the nonlocal and the nonlinear parameters are different.Meanwhile,we simulate the evolution of the refractive index along the axiszwhen the spatial optical solitons are multi-pole solitons.Finally,we study the relation between the power of soliton and the propagation constant under different degree of nonlocality.The power of the single bright soliton does not monotonically increase with the increasing propagation constant when the degree of nonlocalityd3is 10.We also derive the relation between the power of dipole bright solitons with the cubic nonlinearity parameter and the propagation constant under different degree of nonlocality.The power decreases monotonically with the increasing propagation constant when the cubic nonlinearity is a certain value or with the increasing cubic nonlinearity when the propagation constant is a certain value.

nonlocal nonlinear effect,spatial optical solitons,stability

PACS:42.70.Nq,42.65.Sf

10.7498/aps.66.054208

∗浙江省自然科学基金重点项目(批准号:LZ15A050001)和国家自然科学基金(批准号:11675146)资助的课题.

†通信作者.E-mail:linji@zjnu.edu.cn

*Project supported by the National Natural Science Foundation of Zhejiang Province,China(Grant No.LZ15A050001)and the National Natural Science Foundation of China(Grant No.11675146).

†Corresponding author.E-mail:linji@zjnu.edu.cn