ZnO-Bi2O3系压敏陶瓷缺陷弛豫特性的研究进展∗

赵小强 赵学童许超 李巍巍 任路路 廖瑞金 李建英

1)(重庆大学电气工程学院,输变电装备及系统安全与新技术国家重点实验室,重庆 400044)

2)(重庆大学计算机学院,重庆 400044)

3)(国网四川省电力公司电力科学研究院,成都 610072)

4)(西安交通大学电气工程学院,电力设备电气绝缘国家重点实验室,西安 710049)

ZnO-Bi2O3系压敏陶瓷缺陷弛豫特性的研究进展∗

赵小强1)2)赵学童1)†许超1)李巍巍3)任路路1)廖瑞金1)李建英4)

1)(重庆大学电气工程学院,输变电装备及系统安全与新技术国家重点实验室,重庆 400044)

2)(重庆大学计算机学院,重庆 400044)

3)(国网四川省电力公司电力科学研究院,成都 610072)

4)(西安交通大学电气工程学院,电力设备电气绝缘国家重点实验室,西安 710049)

(2016年10月6日收到;2016年11月1日收到修改稿)

由于具有良好的非欧姆特性,ZnO压敏陶瓷被广泛用于电子线路和电力系统的浪涌吸收和瞬态过电压抑制,因此,ZnO压敏陶瓷材料的发展一直备受国内外学者和业界的关注.然而,ZnO压敏陶瓷内部的缺陷结构及其引起的弛豫过程与ZnO压敏陶瓷电性能之间的关联还不清楚,一直是研发新型ZnO压敏陶瓷所要面临的挑战.本文综述了ZnO压敏陶瓷的缺陷类型、理论计算,着重分析了不同缺陷的相应弛豫表征方法,并对ZnO压敏陶瓷的缺陷弛豫机理及其与电老化特性的关联等方面进行了评述.

ZnO压敏陶瓷,缺陷结构,弛豫机理,电性能

1 引 言

压敏陶瓷,通常是指电阻值与外施电压成显著非欧姆关系的半导体陶瓷[1].ZnO-Bi2O3系压敏陶瓷是其中性能最优、应用最广和最具代表性的一种,由于其具有较高的非线性系数,常用来抑制电子线路和电力系统中的瞬态过电压和浪涌电流[2,3].ZnO压敏陶瓷的I-V特性与晶界密切相关,早在二十世纪五十年代,人们就开始研究二元体系的ZnO压敏陶瓷的晶界特性[4].1971年,日本学者Matsuoka[5]提出标准的ZnO压敏陶瓷五元配方,制备出了高非线性系数(50-100)的压敏陶瓷,该配方在电力行业中得到了广泛的应用.从此之后,对于ZnO压敏陶瓷导电理论的研究开始逐步深入,并开始关注晶粒和晶界处的缺陷结构,提出了双Schottky势垒理论模型,解释其电导特性、高非线性以及电容特性等[6-8].

在ZnO压敏陶瓷的制备过程中,由于Zn和O的非化学计量比以及外施添加剂的作用,通常会在ZnO压敏陶瓷体内引入本征和非本征的缺陷,如本征的锌填隙、氧空位和非本征的晶界缺陷等[9-11].这些缺陷往往形成具有不同深度的陷阱中心,在外施电压的作用下俘获和发射电子,对ZnO压敏陶瓷的电子穿越势垒和介电弛豫过程产生重要的影响[12].

目前,关于ZnO压敏陶瓷导电机理的研究已经比较深入,主要有空间电荷限制电流模型[5]、Nordheim-Fowler隧穿模型[4]、双Schottky势垒模型[13]、二步传输模型[6]、空穴诱导击穿模型[8,14]以及两步传输理论等[15],有效地描述了ZnO压敏陶瓷的电子输运过程,解释了宏观的非欧姆导电现象,也已有学者对此进行了大量的总结和评述[2,16-18].与此相比,对ZnO压敏陶瓷中缺陷弛豫研究的关注明显不够,已有的文献主要报道了ZnO压敏陶瓷缺陷弛豫的表征方法,比如介电损耗谱[19]、导纳谱[20],热刺激电流[21]和深能级瞬态谱等[22]方法都可以观测到ZnO压敏陶瓷的弛豫现象.在缺陷理论计算方面,学者们主要通过第一性原理对ZnO本征点缺陷进行了分析,认为施主型缺陷主要决定着ZnO的特性,也是其半导化的主要原因[23,24].近期又有文献报道了掺杂改性、气氛处理等方式对ZnO压敏陶瓷缺陷弛豫的影响[25-27],试图通过这些方法调控缺陷结构,以改善电性能,获得通流能力更强和老化特性更优的ZnO压敏陶瓷.也有学者研究了大电流冲击老化过程对ZnO压敏陶瓷缺陷弛豫和电稳定性能的影响[28].

显然,缺陷弛豫过程与ZnO压敏陶瓷的电性能密切相关.本文将详细地论述ZnO压敏陶瓷缺陷弛豫的相关理论计算与不同表征方法,并讨论不同缺陷的弛豫机理、分析不同的缺陷弛豫过程与电老化性能之间的关联.

2 ZnO压敏陶瓷的缺陷结构

2.1 缺陷结构和电性能

ZnO压敏陶瓷的晶粒是一种极性半导体材料,理论密度为5.7 g/cm3.如图1所示,ZnO具有六方晶系纤锌矿结构,Zn和O都是四面体配位,由O原子镶入Zn的立方密堆积,其中Zn原子占据一半的四面体空隙,所有的八面体空隙和一半的四面体空隙是空的,因而容易引入外部的杂质.纤锌矿的这种开放结构对缺陷的性质和扩散机理有重要的影响[12].纯净且严格符合化学计量比的ZnO带隙较宽,室温下的禁带宽度约为3.37 eV,是绝缘体而非半导体,但实际制备的ZnO陶瓷由于复杂的处理过程和生产工艺,材料偏离理想的化学计量比,ZnO开放的晶体结构使其本身容易产生一定的晶格缺陷,形成局部能级,图2所示为ZnO晶体本征的缺陷结构能带图[16].

ZnO是n型本征半导体,本征缺陷对其性能产生着重要的影响,很多学者从ZnO本征点缺陷的原子几何结构、电子结构及形成能等方面进行了实验和理论计算研究[23,30].通常认为ZnO的本征点缺陷有以下几种形态：氧空位(VO)、反位氧(OZn)、锌填隙(Zni)、氧填隙(Oi)、反位锌(ZnO)及锌空位(VZn).形成n型ZnO的条件为：1)施主能级(Zni,VO,ZnO)位于导带能级下较浅的位置;2)施主能级必须有较低的形成能,即使Fermi能级在禁带中处于较高的位置,施主缺陷也可以大量产生;3)VZn,Oi等电子复合中心的形成能足够高,以确保即使Fermi能级在禁带中的位置较高时,复合中心也难以形成.Oba等[23]采用第一性原理平面波赝势法计算了ZnO本征缺陷的电子结构和形成能,认为施主型缺陷如Zni,VO,ZnO的形成能很低,在ZnO中很容易形成,其中VO的形成能最低,在缺陷数量上占主导,但是VO的能级较深,对电导的贡献不大,认为Zni才是ZnO n型化的主因.

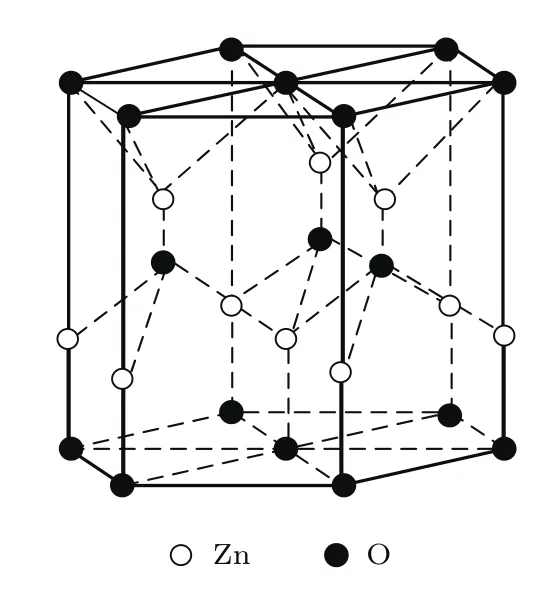
图1 ZnO纤锌矿结构[29]Fig.1.Wurtzite structure of ZnO[29].

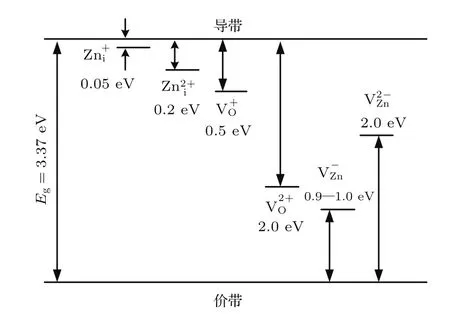
图2 非化学计量比ZnO晶体本征缺陷能级[16]Fig.2.Intrinsic defect level of non-stoichiometric ZnO crystal[16].

图3为Janotti和van de Walle[31,32]利用第一性原理的方法,对富氧和富锌条件下ZnO中的各种本征点缺陷的形成能进行了计算,也认为VO处于深能级,不是ZnO n型化的主要原因,但是会在p型掺杂的ZnO能带中产生补偿中心,破坏ZnO的p型化.Look和Claflin[24]得出类似的结果,Zni和VO是ZnO中两种典型的施主型缺陷,VO形成能低,但所处能级偏深;Zni形成能较高,但容易和其他堆垛层错等缺陷组合形成一种低形成能的复合缺陷,因此,相对而言,Zni对导电的贡献更大.Eda[33,34]认为在这些本征缺陷中,Zni具有最快的扩散速率,成为ZnO晶体中最为常见的缺陷,使单晶的ZnO晶粒呈现出n型半导体的特性,并且对电稳定性有重要的影响.Kohan等[35]采用类似的方法对ZnO的本征缺陷进行研究,结果表明OZn和ZnO的形成能很高,不是主要缺陷;Oi具有形成能高、稳定性差的特点,也不是主要缺陷;而VZn是与VO存在竞争的一种主要空位型缺陷,也即富Zn区VO是主要缺陷,富O区VZn是主要缺陷.

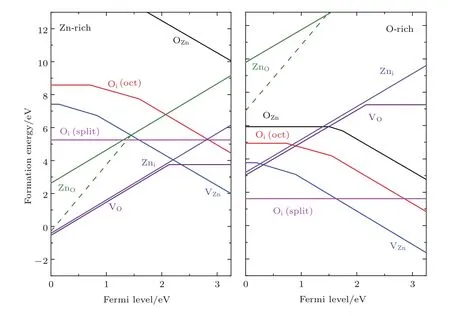
图3 (网刊彩色)本征缺陷形成能随费米能级变化的曲线[31]Fig.3.(color online)Calculation defect formation energy for the main native point defects in ZnO as a function of the Fermi level[31].

目前的理论研究表明,与ZnO本征缺陷相关的很多问题还处于争论中,可以明确的是ZnO的本征缺陷中施主型缺陷(如Zni,VO等)占主导,对ZnO的n型化起了重要作用.但由于缺少一定的实验验证,到底哪种缺陷是ZnO半导化的主导因素还存在争议.

ZnO压敏陶瓷除了由非化学计量比引起的本征点缺陷外,还有外施添加剂引起的缺陷.当外施添加剂有Bi2O3或Pr2O3的添加时,ZnO陶瓷开始显现出非线性的I-V特性,也即是说外施添加剂是ZnO陶瓷非线性的诱导因素或来源,本文主要讨论Bi系的ZnO压敏陶瓷.在添加剂的原子半径与Zn或O差不多的情况下,添加剂倾向于与其尺寸相近的原子发生替代反应,形成替位杂质.如果添加剂的原子半径比Zn或O小很多时,则容易形成间隙杂质.实际上,掺杂作用还会形成一些具有深能级的杂质离子,这种杂质离子能够俘获可移动的电子或空穴,成为陷阱中心,同时也是载流子的色散中心.因此,掺杂作用可以引入新的受主或施主缺陷,称为ZnO压敏陶瓷的非本征缺陷,可以有效地调节载流子浓度和改善ZnO压敏陶瓷的电性能.

由此,Gupta和Carlson[36]提出了ZnO压敏陶瓷的晶界缺陷模型,如图4所示.势垒的耗尽层主要由带正电的稳态的施主离子(D为Bi,Sb等)、氧空位离子和亚稳态的锌填隙离子构成,这些正离子分布在晶界两侧的晶粒耗尽层,晶界面附着带正电的受主离子,如本征的锌空位和氧填隙.由于电中性,晶界面上带负电荷的受主离子与晶界两侧耗尽层正的施主离子相平衡.替位离子和氧空位离子位于ZnO纤锌矿结构的格点位置,相对稳定,而锌填隙离子则容易迁移.在外施电、热或光的作用下,这些缺陷常发生化学反应,从而影响ZnO压敏陶瓷的电性能.

ZnO压敏陶瓷电性能(I-V)如图5所示,按电流密度的大小,将I-V特性分为预击穿区(小电流区)、击穿区(中电流区)和回升区(大电流区)[2,3].预击穿区以热发射电子为主,I-V特性曲线几乎呈线性,压敏陶瓷表现为绝缘态;击穿区以隧道电流为主,I-V特性中表现出明显的非线性,电压变化不大的情况下,电流急剧上升,也可以看成晶界被击穿;回升区,被击穿的晶界几乎不分担电压,大部分压降施加于晶粒之上,电流-电压关系服从欧姆定律,主要由晶粒电阻决定[2,3,37].

图4 Schottky势垒和缺陷结构的电响应[36]Fig.4.Electrical responses of Schottky barrier and defect structure[36].

为了衡量击穿区压敏陶瓷的压敏特性,也即非线性的大小,提出了非线性系数η,工程上常用下式对其进行计算[37]：

其中,U2和U1为压敏陶瓷流过电流为I2和I1时对应的电压值,通常情况下I2和I1的值分别取1和0.1 mA.并定义1 mA电流所对应的电压为压敏电压,记为U1mA.单位厚度的压敏电压称为电位梯度,记为E1mA.

图5 ZnO压敏陶瓷电场强度与电流密度(J-E)的关系曲线[36]Fig.5.J-Ecurves of ZnO varistor ceramics[36].

2.2 ZnO压敏陶瓷显微结构

ZnO压敏陶瓷由半导电的ZnO晶粒(电阻率约为0.1-10 Ω·cm[16])和绝缘的晶界构成,显微结构可以直观地表示为图6(a).ZnO晶粒占所有90%以上的体积,晶粒大小约为10-20µm,包围晶粒的为高阻态的晶界和晶间相.除了晶粒和晶间相,还包括少量的微粒和气孔.

纯ZnO多晶陶瓷的I-V特性为线性,为使其呈非线性,需添加各种氧化物.这些氧化物添加剂在ZnO晶粒或晶界处形成缺陷[40].由于添加剂在相邻ZnO晶粒之间及在多个晶粒接触处的汇聚,晶界处的显微结构十分复杂[41].Eda[39]大致将晶界区域分为三个区,如图6(b)所示.I区的晶粒边界有一层较厚的富Bi晶界层(0.1-1.0µm);II区的富Bi晶界层较薄(1-100 nm);III区最薄,常常观察不到明显的晶界偏析层,仅有几层原子厚的偏析杂质离子.由于晶界结构的紊乱、化学计量比的偏离和杂质的富集,在ZnO晶粒表面处形成大量受主型表面态,成为俘获晶粒中自由电子的陷阱中心.

图6 ZnO压敏陶瓷显微结构 (a)SEM图[38];(b)微观示意图[39]Fig.6. Microstructure of ZnO varistor ceramics：(a)SEM[38];(b)microscopic diagram[39].

3 ZnO压敏陶瓷缺陷的弛豫表征

3.1 ZnO压敏陶瓷缺陷的弛豫损耗频谱

介电弛豫损耗频谱是研究电介质材料弛豫机理的有效方法,而弛豫机理与电介质材料的显微结构和缺陷结构密切相关,1976年,Levinson和Philipp[19]测量了ZnO压敏陶瓷30 Hz＜f＜108Hz范围内的弛豫特性,发现弛豫损耗频谱在室温下3×105Hz附近出现峰值,如图7所示,该弛豫损耗峰具有扩展德拜损耗的特征.尽管tanδ峰值的具体大小及出现峰值的具体频率与材料的组分及工艺有关,但是,在室温条件下,所有配方及工艺制备的ZnO压敏陶瓷,其介电频谱均在105Hz附近出现该损耗峰,因此认为该弛豫损耗峰与ZnO的本征缺陷直接相关.

图7 ZnO压敏陶瓷室温损耗频谱[19]Fig.7.Dissipation factor tanδversus frequency at room temperature[19].

图8 (网刊彩色)ZnO压敏陶瓷试样在-100◦C-20◦C的介电频谱(a);本征缺陷弛豫峰1和峰2对应的活化能级(b)[44]Fig.8.(color online)Dielectric frequency spectra of ZnO varistor ceramics at-100◦C-20◦C(a),and the activation energies of relaxation loss peak 1 and peak 2(b)[44].

Levinson和Philipp[19,42]研究了不同温度下ZnO压敏陶瓷的介电频谱后,分析了交流电导和介电损耗随频率和温度的变化规律,认为温度高于77 K后损耗峰与夹层极化无关,排除了Maxwell-Wagner效应和杂质离子弛豫过程,认为可能是晶界电子能级的响应.由于当时对ZnO压敏陶瓷晶界缺陷模型的认识尚不深入,Levinson和Philipp的理论研究受到了很大限制,但他们的实验结果仍具有重要意义.Cordaro等[43]进一步提出该损耗峰可能起源于与本征点缺陷有关的电子陷阱对电子的俘获和发射过程.

如图8所示,Cheng等[44]通过测量ZnO压敏陶瓷10-1Hz＜f＜107Hz,-100°C＜T＜20°C范围内的介电谱,发现原来在105Hz附近出现的弛豫损耗峰在低温分裂成了两个峰(峰1和峰2),通过计算得到这两个峰对应的活化能分别为0.26和0.36 eV,Cheng还通过热刺激电流法对这两个能级进行了验证,得到了同样的结果.

3.2 ZnO压敏陶瓷缺陷的弛豫导纳频谱与温谱

根据Blatter和Greuter[14,45]的研究,如果ZnO压敏陶瓷内浅陷阱密度远大于深陷阱密度,则零偏电导和电容的关系符合简单的Debye公式：

式中,G为电导,σ0为零偏直流电导,ω为角频率,CHF为高频电容,nv为深陷阱密度,τv为弛豫时间,可表示成下式：

Nc为导带有效态密度,σn是俘获截面,vth为电子的热激发速度,gv(=1/2)为陷阱态简并度的倒数,Ec-Evt为导带下陷阱深度,k为玻尔兹曼常数,T为测量温度.

Chiou和Chung[20]采用导纳频谱观测了G/ω随角频率ω的变化,也观测到了ZnO压敏陶瓷的缺陷弛豫现象,如图9所示,在低温-60°C-0°C的范围内,发现导纳谱中存在着两个弛豫峰--峰1和峰2.并根据(3)式计算了这两个弛豫峰对应的活化能.如表1所示,峰1和峰2对应的活化能级分别为0.245和0.31 eV,与前面弛豫损耗谱计算的结果相差不大.在室温条件下,峰1的弛豫时间比峰2小了两个数量级,俘获截面大小接近.0.31 eV对应的弛豫峰在ZnO压敏陶瓷中被多位学者报道[46,47],该峰不随添加剂而变化,被认为与ZnO的一价氧空位缺陷电离相关.

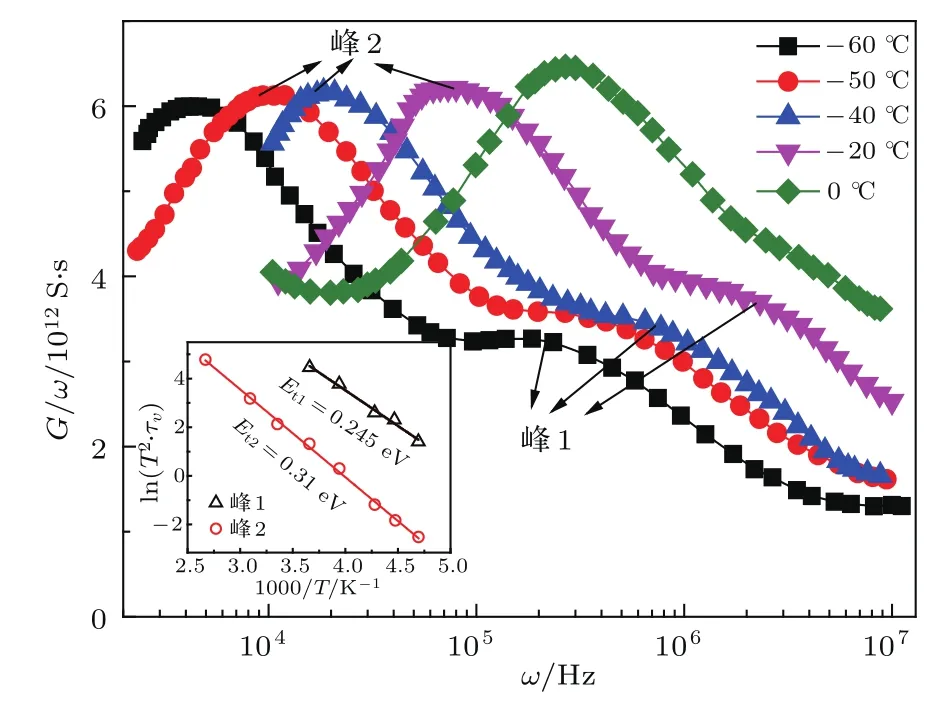
图9 (网刊彩色)ZnO压敏陶瓷导纳在-60◦C-0◦C范围的频谱图,插图为两个导纳弛豫峰对应的活化能[20]Fig.9.(color online)Conductance/frequency,G/ω,vs angular frequencyωat from-60◦C-0◦C;The Arrhenius plot ln(T2·τ)vs 1000/Tin the inset[20].

表1 室温条件下两个缺陷能级对应的弛豫时间和俘获截面[20]Table 1.Relaxation time and capture cross section of the two defect levels at room temperature[20].

图10 (网刊彩色)ZnO压敏陶瓷导纳在10-100 kHz范围的温谱图,插图为两个导纳弛豫峰对应的活化能[43]Fig.10.(color online)ConductanceGvs temperatureTfor ZnO varistor ceramics.Frequencies covered are 10-100 kHz.Activation plot of ln(ω/T2)as a function of reciprocal temperature[43].

Cordaro等[43]则通过实验,对不同配方的ZnO压敏陶瓷在1 Hz＜f＜106Hz,30°C＜T＜350°C范围内的导纳谱测量后发现,电导曲线随温度的变化均出现两个峰值,对应活化能分别为0.17和0.33 eV(图10).他们同样排除了Maxwell-Wagner效应的影响,提出这两个峰可能是由本征缺陷引起的.表2为Cordaro等计算得到的导纳温谱弛豫峰的电参数,与表1导纳频谱的结果类似.这表明在用导纳谱表征压敏陶瓷缺陷弛豫时,不同温度下的导纳频谱与不同频率下的导纳温谱具有一致性.Cordaro认为峰1对应的活化能0.17 eV与其他学者报道的0.20 eV的活化能接近,进一步提出该弛豫峰对应着ZnO本征的二价锌填隙缺陷,如(4)式所示：

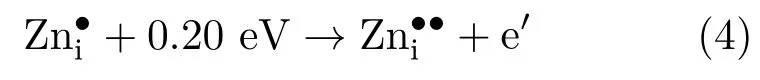
表2 室温条件下两个缺陷能级对应的弛豫时间和俘获截面[43]Table 2.Relaxation time and capture cross section of the two defect levels at room temperature[43].

3.3 ZnO压敏陶瓷缺陷弛豫的热刺激电流(TSC)表征

随着对ZnO压敏陶瓷缺陷弛豫认识的深入,人们认为ZnO压敏陶瓷的本征缺陷离子极化可能属于热离子极化的范畴.在弛豫损耗谱及导纳谱测量中,由于测试温度较低,在测试频率范围内难以形成可观测的热离子极化电流.如果给ZnO压敏陶瓷施加较高的极化电压,并保持一定的时间,耗尽层中的缺陷离子将沿着电场的方向向晶粒表面扩散,形成热离子极化.然后迅速冷却至低温,使热离子基本“冻结”.最后撤去外施极化电压,并以一定的速度升温.随着温度的升高,缺陷离子逐渐解冻,并反向扩散,在外电路中就可以检测到明显的退极化电流.也就是说可以通过TSC检测ZnO压敏陶瓷中缺陷离子的热离子极化,并与介电谱相对照,这样就可以验证介电谱测量中所反映的弛豫极化机理.

如图11所示,Zhang等[21]通过TSC方法测量,观测到ZnO压敏陶瓷在-25°C和35°C附近出现两个明显的退极化电流峰P1和P2,并认为这两个峰与ZnO压敏陶瓷的本征缺陷相关.Zhang等又进一步研究了直流偏压和大电流冲击老化对ZnO压敏陶瓷TSC的影响,发现直流偏压将提高退极化电流峰的高度,而大电流冲击老化后ZnO压敏陶瓷会出现新的退极化电流峰,并把该新出现的电流峰归因于大电流冲击老化导致的一价锌填隙离子的迁移.

Cheng等[44]在对ZnO压敏陶瓷进行TSC测量时发现了三个退极化电流峰值,如图12所示,分别位于-25°C,30°C和115°C附近,低温的两个峰值出现的位置与Zhang的结果类似.Cheng等采用初期上升法对这三个峰对应的活化能进行了计算,得到结果分别为0.26,0.36和0.52 eV,其中低温两个峰对应的活化能级与在弛豫损耗谱计算的ZnO压敏陶瓷的两个损耗峰活化能一致[44],这也就进一步表明ZnO压敏陶瓷低温的两个弛豫峰符合热离子弛豫极化的机理.Cheng等认为115°C附近的退极化电流峰的能级与一价锌填隙离子的迁移活化能接近.

图11 ZnO压敏陶瓷TSC谱图[21]Fig.11.TSC spectra of ZnO varistor samples[21].

图12 ZnO压敏陶瓷TSC谱图[44]Fig.12.TSC spectra of ZnO varistor samples[44].

3.4 ZnO压敏陶瓷缺陷弛豫的深能级瞬态谱(DLTS)表征

DLTS也常被用来分析ZnO压敏陶瓷缺陷弛豫过程,它可以方便地测量出缺陷在不同温度下的弛豫时间,从而得到缺陷在禁带中的位置、密度和俘获截面等参数.

如图13所示,Shohata等[50]率先采用DLTS对ZnO压敏陶瓷缺陷弛豫特性进行测试,在100-200 K的温度范围内发现了两个峰值,这两个峰随外施偏压的增大而增高,通过计算发现这两个弛豫峰的活化能分别为L1=0.24 eV和L2=0.33 eV,与采用其他测量方法获得的结果相接近.在图14中,Wang等[48]在更宽的温度范围内测量了ZnO压敏陶瓷的DLTS谱,发现了三个峰值,并给出了这三个峰值对应的电参数,如表3所示.计算得到它们的活化能分别为L1=0.11 eV,L2=0.27 eV和L3=0.94 eV,其中L1,L2比损耗谱和导纳谱测得的结果略小,峰1对应的俘获截面与导纳谱相比也小了近三个数量级.L3是一个新发现的峰,并认为该峰可能与ZnO内二价的氧空位缺陷有关.

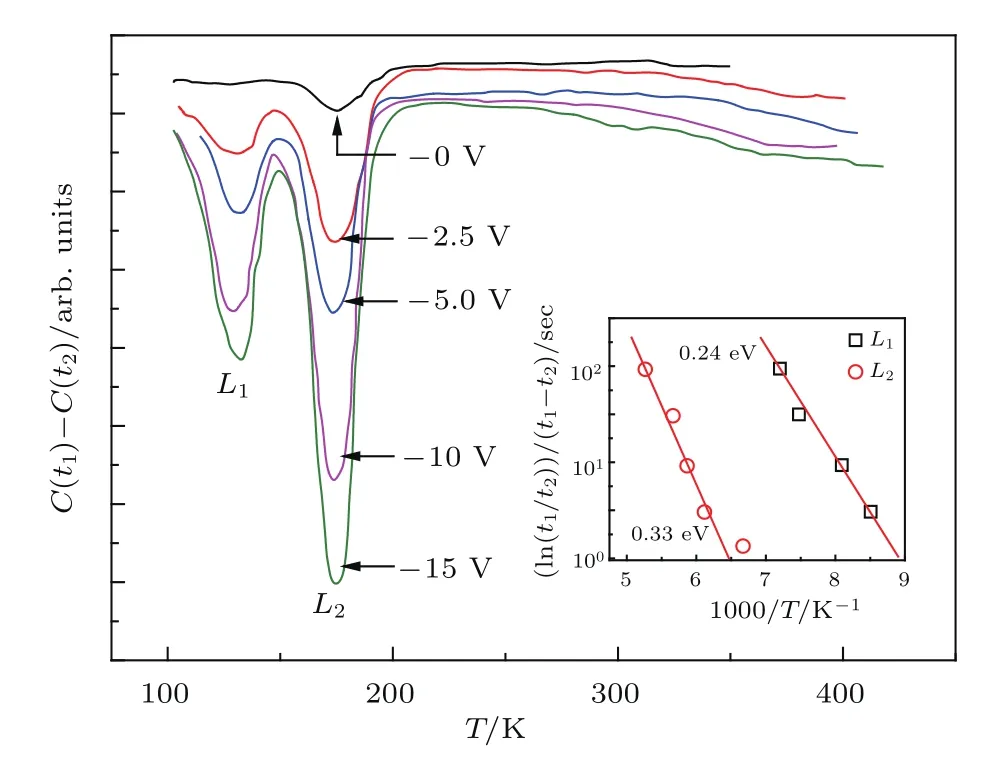
图13 (网刊彩色)ZnO压敏陶瓷在不同的偏压条件的DLTS谱图,插图为弛豫峰对应的活化能[22]Fig.13.(color online)DLTS spectrum of ZnO varistor ceramics at various voltages,and the activation energy calculation is in the inset[22].

表3 ZnO压敏陶瓷弛豫峰对应的缺陷能级、陷阱密度和俘获截面[48]Table 3. Defect levels,trap density and capture cross section of the relaxation peaks in ZnO varistor ceramics[48].

表4进一步给出了不同学者采用不同测试方法得到的ZnO压敏陶瓷的缺陷能级和缺陷类型,可以发现,DLTS法测得的低温两个缺陷弛豫的活化能相对于其他测试方法略小,这两个缺陷弛豫峰普遍被认为对应于ZnO压敏陶瓷本征的二价锌填隙和一价氧空位缺陷.但DLTS同时可以在高温区测得损耗谱和导纳谱观测不到的新缺陷弛豫峰,并且该弛豫峰的活化能远高于低温两个本征缺陷的活化能.

图14 ZnO压敏陶瓷的DLTS谱图,插图为峰值对应的活化能[48,49]Fig.14.DLTS spectrum of ZnO varistor ceramics,and the activation energy calculation is in the inset[48,49].

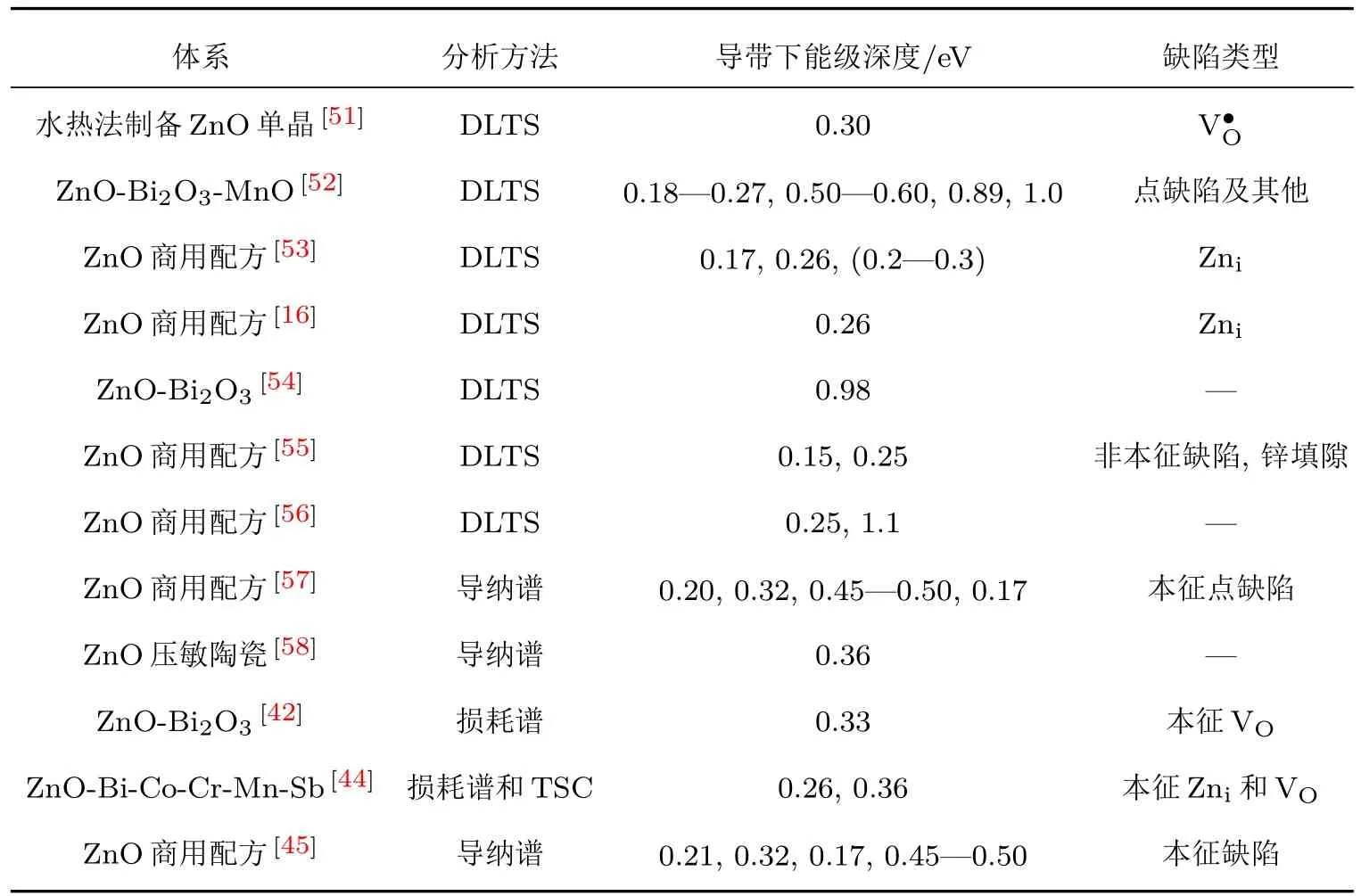
表4 不同配方及测试方法对ZnO压敏陶瓷缺陷结构的表征Table 4.Characterization of various ZnO varistor ceramics with different test methods.

4 ZnO压敏陶瓷缺陷结构的弛豫机理

4.1 Cole-Cole方程在ZnO压敏陶瓷中的应用

在电介质材料中,如果陷阱具有确定的发射率即弛豫时间,就属于具有单一弛豫时间的Debye型弛豫.而在压敏陶瓷材料中往往存在着多种缺陷弛豫,并且弛豫过程与Debye方程并非完全一致.事实上,由于介质的结构、分子所处状态、分子间的作用力以及热运动等的影响,介质中所有偶极子的弛豫状态有所不同,每个偶极分子在不同瞬间具有本征弛豫时间,实验测量出来的是整个介质的平均值,因而实际介质的弛豫时间是围绕其最大概率值的一个分布.由此,Cole-Cole给出了具有分布弛豫时间的复介电常数修正经验公式,表示为[59]

将(5)式的实部和虚部分开,表示为ε∗=ε′-iε′′,可得介电常数虚部ε′′的表达式

式中,εs,ε∞为静态介电常数和光频介电常数;ω,τ0为角频率和分布弛豫时间的最大概率值;α为0-1之间的常数,表示弛豫时间的分散程度,α=1时对应Debye弛豫.

在实际测量中,介质损耗不仅含有弛豫极化的响应,还要考虑电导的贡献.对ZnO压敏陶瓷而言,需要考虑二价锌填隙和一价氧空位两种本征缺陷弛豫过程和电导的共同作用,可得损耗因子的表达式为[38]

式中,ε0为真空介电常数,σdc为直流电导率.

图15为Zhao等[38]利用(7)式对ZnO压敏陶瓷介质损耗谱进行的分析,可以把不同频率下的损耗分解成三个部分,也即弛豫峰1、峰2和直流电导的贡献.其中,峰1和峰2分别对应着ZnO压敏陶瓷的本征锌填隙和氧空位缺陷,低频区损耗主要是直流电导的贡献.很明显,ZnO压敏陶瓷在低温测量条件下的弛豫过程是满足Cole-Cole弛豫理论的.

4.2 Havriliak-Negami(H-N)方程在ZnO压敏陶瓷中的应用

Tsonos等[60]提出采用H-N理论对ZnO压敏陶瓷的缺陷弛豫进行解释,H-N方程可写作以下形式：

式中,Aω-n为直流电导的贡献,Im表示式中该部分为虚部,τ0为弛豫时间,α(0＜α＜1)和β(0＜β＜1)为弛豫时间的分散度,值得指出的是如果仅当α=0,0＜β＜1时,(8)式就遵循Cole-Davidson方程;当α=0,且β=1时,H-N方程就成了Debye方程.为每个弛豫过程对复介电常数实部的贡献,τ0k为弛豫时间.图16为采用(8)式对233 K温度下测得的数据进行的拟合分析,结果表明采用H-N方程也可以较好地描述ZnO压敏陶瓷在低温时的弛豫过程,但是表5的拟合参数显示,对弛豫峰1和峰2的拟合参数α值均为0,符合α=0,0＜β＜1的条件,也即ZnO压敏陶瓷在低温的弛豫过程其实是符合Cole-Davidson弛豫方程的.

图16 (网刊彩色)ZnO压敏陶瓷弛豫损耗谱的H-N拟合[60]Fig.16.(color online)H-N fitting results of ZnO varistor ceramics[60].

表5 ZnO压敏陶瓷弛豫峰1和峰2在(8)式的拟合参数值[60]Table 5.Electrical parameters of relaxation peak 1 and 2 in ZnO varistor ceramics fitted by using function(8)[60].

4.3 Cole-Davidson电模量方程在ZnO压敏陶瓷中的应用

近期的研究表明[38,61-63],基于Cole-Davidson分布的电模量方程在描述ZnO压敏陶瓷缺陷弛豫时更具有优势,它不仅可以用来描述低温缺陷弛豫过程,还可以抑制高温条件下介质中增大的电导对缺陷弛豫过程的影响,是一种描述高温区缺陷弛豫的有效方法[63].电模量方程可以描述为如下形式[64,65]：

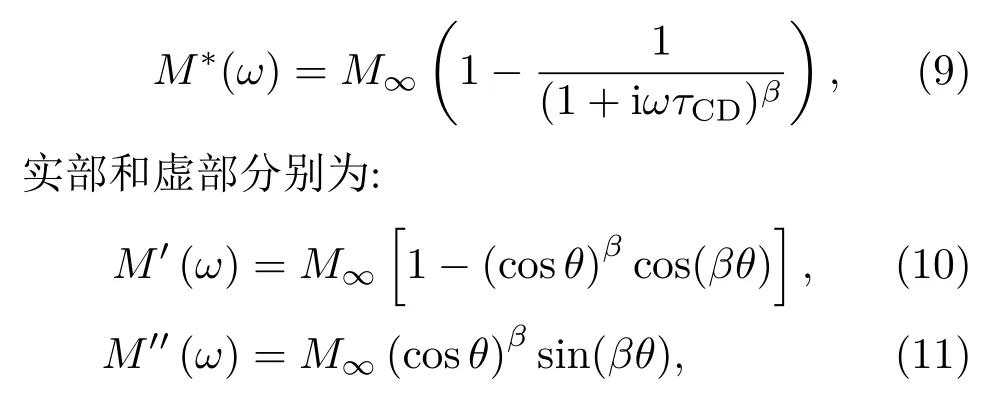
式中,M′,M′′分别对应着复电模量M∗的实部和虚部,M∞对应着电模量的高频极限值,θ=arctan(ωτCD),τCD为弛豫时间,β为0-1之间的常数,代表着弛豫时间常数的分散度.图17结果显示,在四元ZnO压敏陶瓷的电模量谱图中,可以观测到四个不同的缺陷弛豫峰[38].Zhao等[66]在对商用ZnO试样进行测量时,发现了四个弛豫过程,只不过峰3和峰4在高温423 K以上被发现.峰1和峰2的活化能级与弛豫损耗谱中结果一致,在0.24和0.35 eV附近且不随配方和制备工艺而改变,对应着ZnO压敏陶瓷的本征锌填隙和氧空位缺陷.而峰3和峰4的活化能则是可变的,Andres-Verges和West[62]在电模量谱图中测得这两个峰对应的活化能分别在0.64和0.94 eV,Zhao等[66]在商用试样中测得的结果为0.72和0.84 eV,这两个峰被归因于非本征的缺陷弛豫,认为与ZnO压敏陶瓷的晶间相和晶界面缺陷有关.从图17的拟合结果可知,电模量可以很好地描述ZnO压敏陶瓷的缺陷弛豫过程,并且可以在更宽的温度范围内更全面地对ZnO压敏陶瓷的缺陷弛豫过程进行表征.

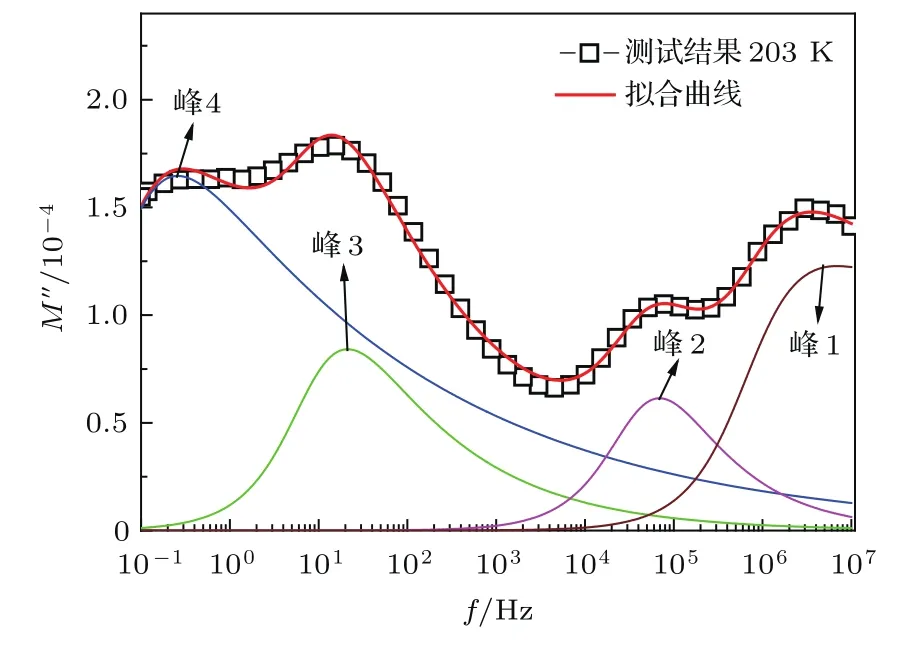
图17 ZnO压敏陶瓷弛豫电模量谱拟合[38]Fig.17.Electrical modulus fitting results of ZnO varistor ceramics[38].

5 ZnO压敏陶瓷缺陷结构弛豫与电老化特性的关联

以往,对ZnO压敏陶瓷老化特性的研究主要是关注压敏电压、非线性系数、漏电流等电参量随外施交流、直流、冲击电压的老化规律,并提出了离子迁移模型[67]和氧解吸附等[68]理论对其进行解释.近期有学者尝试从缺陷弛豫的角度对ZnO压敏陶瓷的老化进行研究,Eda等[34]研究了交、直流老化对ZnO压敏陶瓷室温弛豫损耗谱的影响,如图18所示.交、直流老化后试样损耗峰几乎没有变化,仅仅是低频损耗明显的增大.

式中,ε′和ε′′分别为复介电常数ε∗对应的实部和虚部;γ和g分别为直流电导率和交流弛豫等效电导率;ε0,εr为真空介电常数和试样对应的介电常数.由(12)式和(13)式可知[59],交、直流老化主要导致了低频直流电导对弛豫损耗的贡献.图19所示为大电流冲击老化对ZnO压敏陶瓷弛豫损耗的作用[66],在173 K时,老化前后试样都表现出两个弛豫损耗峰,并且峰值出现的频率位置和对应的活化能都未随老化发生变化,低频损耗明显上升.这表明大电流冲击老化与交、直流老化一样,主要影响低频电导对损耗的贡献.

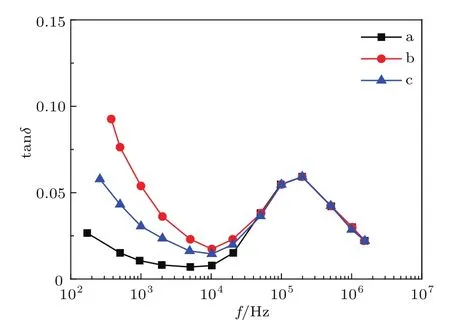
图18 交、直流老化对ZnO压敏陶瓷弛豫损耗谱的影响,a为原试样,b和c分别为在95 V/mm偏压和65 V/mm,343 K条件下老化500 h[34]Fig.18.Degradation phenomena of ZnO varistor ceramics in dielectric loss by dc biasing at 95 V/mm and ac biasing at 65 V/mm at 343 K for 500 h;a,initial;b,after dc biasing;c,after ac biasing[34].

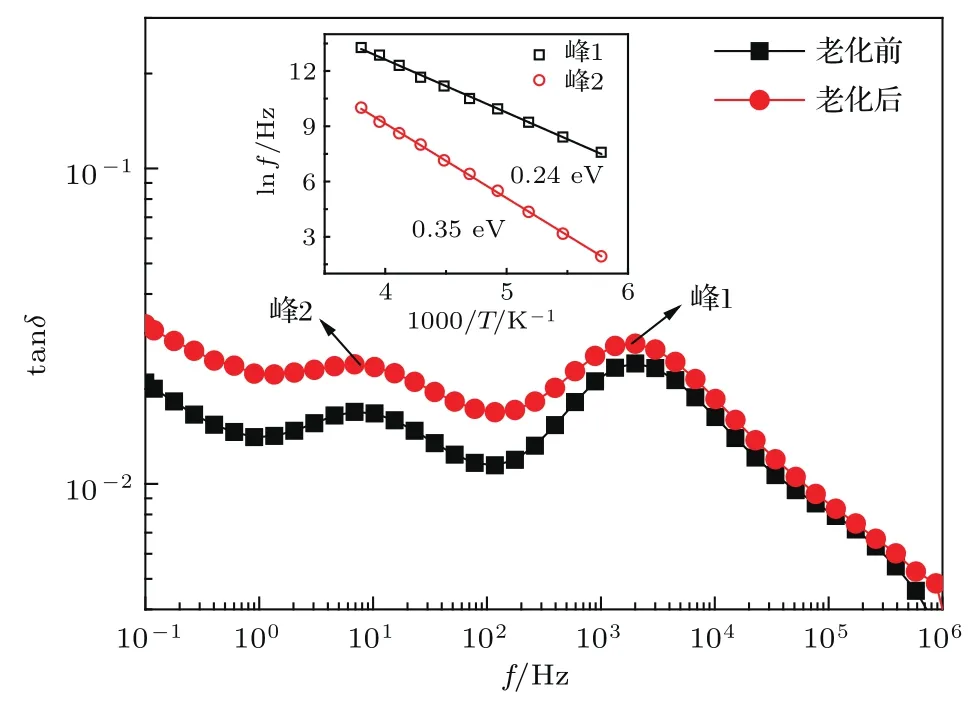
图19 大电流冲击对ZnO压敏陶瓷弛豫损耗谱的影响[66]Fig.19.Degradation phenomena of ZnO varistor ceramics in dielectric loss by impulse current[66].

类似的现象也被Lee和Young[49]通过DLTS测量进行验证,如图20所示,结果表明DLTS中出现了三个弛豫损耗峰,峰1和峰2及其对应活化能在大电流冲击老化前后均未变化,也即表明ZnO压敏陶瓷的本征缺陷与老化之间的关联不大.而高温的峰3认为与晶界面陷阱相关,在老化后峰形状和宽度均发生了变化,相应的ZnO压敏陶瓷的势垒高度也明显下降,这表明峰3对应的缺陷与ZnO压敏陶瓷的电性能密切相关.

图20 大电流冲击对ZnO压敏陶瓷弛豫损耗谱的影响[49]Fig.20.Degradation phenomena of ZnO varistor[49].

根据文献[38,66]报道,商用ZnO压敏陶瓷试样在高温电模量谱中出现两个缺陷弛豫峰--峰3和峰4,分别与非本征的晶间相和晶界面两种缺陷有关.如图21(a)所示,大电流冲击老化后,峰3对应的频率位置变化不大,而峰4则明显的向高频方向移动.峰3对应的活化能在冲击老化前后变化不大,均在0.72 eV附近,但峰4对应的活化能老化后明显的下降,从老化前的0.84 eV下降到老化后的0.76 eV.

电介质材料的缺陷弛豫过程,通常可以用并联的RC电路来等效,由于老化过程主要影响了非本征的缺陷,根据文献[66,69,70]分析,通过电模量谱结合复阻抗平面谱,可以进一步分析得到非本征弛豫峰3和峰4对应的宏观电路参数,阻抗谱和等效电路如图21(b)和图22所示,其中,R1,C1对应弛豫峰3的等效电阻和电容,R2,C2对应弛豫峰4的等效电阻和电容.ZnO压敏陶瓷非本征的缺陷弛豫等效电路,可用(14)式和(15)式来表示[66,69]：

式中Z′,Z′′为复阻抗Z∗的实部和虚部,C0为试样所占空间对应的真空电容.

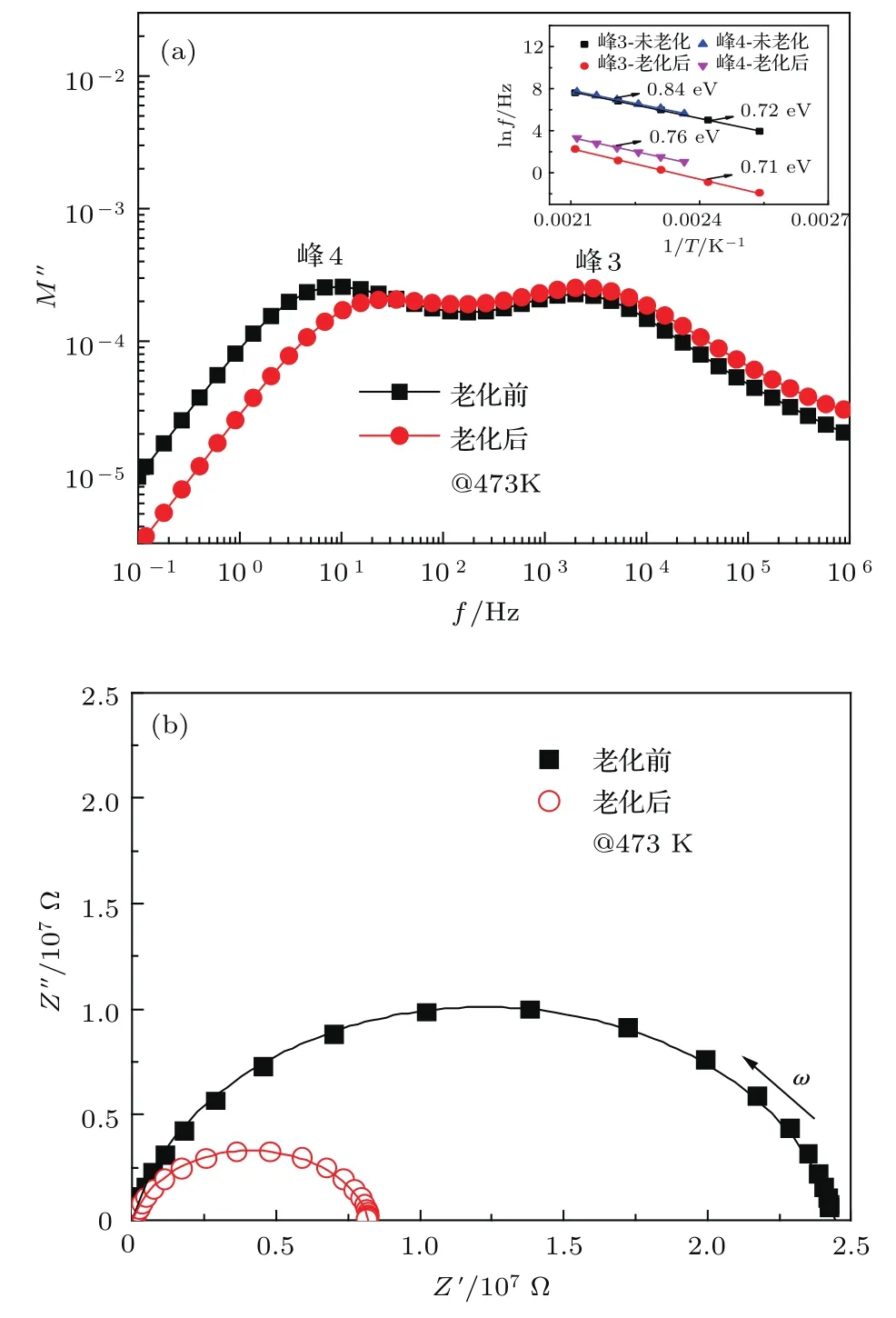
图21 大电流冲击前后ZnO压敏陶瓷高温电模量谱(a),复阻抗谱(b)[66]Fig.21. Electricalmodulus(a)and complex impedance spectra(b)of ZnO varistor ceramics before and after impulse current[66].

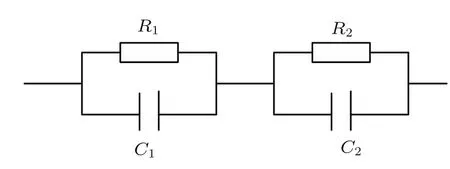
图22 ZnO压敏陶瓷高温非本征缺陷弛豫等效电路分析[66]Fig.22.Equivalent circuit analysis for extrinsic defect relaxations at high temperature[66].

从表6的结果可以看出,弛豫峰4对应的电阻值R2比峰3对应的阻值R1高约两个数量级.大电流冲击老化后,弛豫峰3对应的电路参数R1和C1并未有明显的变化,而弛豫峰4对应的R2和C2老化后则发生了明显变化,R2的阻值降低了约三倍.该结果进一步表明ZnO压敏陶瓷的电性能受控于与晶界界面相关的非本征缺陷弛豫过程.

表6 ZnO压敏陶瓷非本征弛豫峰等效电路参数[66]Table 6.Equivalent circuit parameters of extrinsic relaxation peaks in ZnO varistor ceramics[66].

6 结 论

国内外学者对ZnO压敏陶瓷缺陷结构的研究逐步深入,提出了多种缺陷弛豫的表征方法,并采用不同的理论对不同的缺陷弛豫过程进行了解释,初步得到了微观缺陷结构与其宏观电性能之间的关联.但目前ZnO压敏陶瓷在发展应用的过程中也存在以下需要解决的问题.

1)对ZnO压敏陶瓷缺陷弛豫的表征手段繁多,不同学者得到的结果并不完全相同,需要进一步明确不同的表征方法之间的差异及彼此间是否可以相互验证,也未明确何种表征方法更为有效和全面.

2)目前仍不清楚如何通过调控缺陷结构来优化ZnO压敏陶瓷的电性能.对非本征缺陷的理论计算研究还不足,本征缺陷和非本征缺陷与宏观电性之间的关联仍有争议.

3)目前特高压电力系统的发展,要求具有更高电位梯度的ZnO压敏陶瓷避雷器,进一步认识ZnO压敏陶瓷的缺陷结构和导电机理,是开发高电位梯度的ZnO压敏陶瓷的关键.

[1]Moulson A J,Herbert J M 2003Electroceramics(Vol.2)(Chichester：Wiley)pp150-156

[2]Clarke D R 1999J.Am.Ceram.Soc.82 485

[3]Wang Z L,Li S T 2009Manufacture and Application of ZnO Varistor Ceramics(Beijing：Science Press)pp1-3(in Chinese)[王振林,李盛涛2009氧化锌压敏陶瓷制造及应用(北京：科学出版社)第1-3页]

[4]Levinson L M,Philipp H R 1975J.Appl.Phys.46 1332

[5]Matsuoka M 1971Jpn.J.Appl.Phys10 736

[6]Mahan G D,Levinson L M,Philipp H R 1979J.Appl.Phys.50 2799

[7]Pike G E 1981Mater.Res.Soc.Symp.Proc.5 369

[8]Blatter G,Greuter F 1986Phys.Rev.B34 8555

[9]Choi J S,Yo C H 1976J.Phys.Chem.Solids37 1149

[10]Allsopp H J,Roberts J P 1959Trans.Faraday Soc.55 1386

[11]DupontPavlovsky N,Caralp F,Delhaes P,Amiell J 1976Phys.Status Solidi A35 615

[12]Li S T,Cheng P F,Wang Y P,Zhu B 2007Insulators and Surge Arresters5 19(in Chinese)[李盛涛,成鹏飞,王玉平,朱斌2007电瓷避雷器5 19]

[13]Levin J D 1975CRC Crit.Rev.Sol.Stat.Sci.5 597

[14]Blatter G,Greuter F 1986Phys.Rev.B33 3952

[15]Castro M S,Aldao C M 1993Appl.Phys.Lett.63 1077

[16]Gupta T K 1990J.Am.Ceram.Soc.73 1817

[17]He J L,Cheng C L,Hu J 2016AIP Adv.6 030701

[18]Li J Y,Li S T,Cheng P F,Alim M A 2015J.Mater.Sci.Mater.Electron.26 4782

[19]Levinson L M,Philipp H R 1976J.Appl.Phys.47 1117

[20]Chiou B S,Chung M C 1991J.Electron.Mater.20 885

[21]Zhang M R,Liu F Y,Liu Z Y 1991Proceedings of the 3rd International Conference on Properties and Applications of Dielectric MaterialsTokyo,Japan July 8-12,1991 p513

[22]Tsuda K,Mukae K 1989J.Ceram.Soc.Jpn.97 1211

[23]Oba F,Nishitani S R,Isotani S,Adachi H,Tanaka I 2001J.Appl.Phys.90 824

[24]Look D C,Claflin B 2001Phys.Status Soldi41 624

[25]Lin J J,Li S T,He J Q,Liu W F 2016Int.J.Inorg.Mater.31 981(in Chinese)[蔺家骏,李盛涛,何锦强,刘文凤2016无机材料学报31 981]

[26]Li J Y,Li S T,Liu F Y,Alim M A 2006J.Mater.Sci.:Mater.Electron.17 211

[27]Zhao X T,Li J Y,Jia R,Li S T 2013Acta Phys.Sin.62 077701(in Chinese)[赵学童,李建英,贾然,李盛涛 2013物理学报62 077701]

[28]Zhao X T,Li J Y,Li H,Li S T 2012Acta Phys.Sin.61 153103(in Chinese)[赵学童,李建英,李欢,李盛涛 2012物理学报61 153103]

[29]Addison W E 1953Structural Principles in Inorganic Compounds(New York：Wiley)p57

[30]Erhart P,Albe K,Klein A 2006Phys.Rev.B73 205203

[31]Janotti A,van de WAlle C G 2007Phys.Rev.B76 165202

[32]Janotti A,van de Walle G G 2005Appl.Phys.Lett.87 122

[33]Eda K,Iga A,Matsuoka M 1979Jpn.J.Appl.Phys.18 997

[34]Eda K,Iga A,Matsuoka M 1980J.Appl.Phys.51 2678

[35]Kohan A F,Ceder G,Morgan D,van de Walle C G 2000Phys.Rev.B61 15019

[36]Gupta T K,Carlson W G 1985J.Mater.Sci.20 3487

[37]Levinson L M,Phillipp H R 1974Appl.Phys.Lett.24 75

[38]Zhao X T,Liao R J,Liang N C,Yang L J,Li J,Li J Y 2014J.Appl.Phys.116 014103

[39]Eda K 1989IEEE Electr.Insul.Mag.5 28

[40]Selim A F,Gupta T K,Hower P L,Carlson W G 1980J.Appl.Phys.51 765

[41]Levine J D 1971J.Appl.Phys.42 3991

[42]Levinson L M,Philipp H R 1978J.Appl.Phys.49 6142

[43]Cordaro J F,Shim Y,May J E 1986J.Appl.Phys.60 4186

[44]Cheng P F,Li S T,Zhang L,Li J 2008Appl.Phys.Lett.93 012902

[45]Greuter F,Blatter G 1990Semicond.Sci.Technol.5 111

[46]Shim Y,Cordaro J F 1988J.Appl.Phys.64 3994

[47]Shim Y,Cordaro J F 1988J.Am.Ceram.Soc.71 184

[48]Wang Y P,Lee W I,Tseng T Y 1996Appl.Phys.Lett.69 1807

[49]Lee W I,Young R L 1996Appl.Phys.Lett.69 526

[50]Shohata N,Matsumura T,Ohno T 1980Jpn.J.Appl.Phys.19 1793

[51]Simpson J C,Cordaro J F 1988J.Appl.Phys.63 1781

[52]Leach C,Vernon-Parry K D,Ali N K 2010J.Electroceram.25 188

[53]Rohatgi A,Pang S K,Gupta T K,Straub W D 1988J.Appl.Phys.63 5375

[54]Ohbuchi Y,Yoshino J,Okamoto Y,Morimoto J 1999J.Appl.Phys.38 899

[55]Fan J,Freer R 1994J.Am.Ceram.Soc.77 2663

[56]Winston R A,Cordaro J F 1990J.Appl.Phys.68 6495

[57]Han J,Mantas P Q,Senos A M R 2002J.Eur.Ceram.Soc.22 49

[58]Levinson L M,Philipp H R 1986J.Am.Ceram.Soc.Bull.65 639

[59]Chen J D,Liu Z Y 1982Dielectric Physics(Beijing：Mechanical Industry Press)p151(in Chinese)[陈季丹,刘子玉1982电介质物理学(北京：机械工业出版社)第151页]

[60]Tsonos C,Kanapitsas A,Triantis D,Anastasiadis C,Stavrakas I,Pissis P,Neagu E 2011Ceram.Int.37 207

[61]Hong Y W,Kim J H 2004Ceram.Int.30 1307

[62]Andres-Verges M,West A R 1997J.Electroceram.1 125

[63]Li S T,Wang H,Lin C J,Li J Y 2013Acta Phys.Sin.62 087701(in Chinese)[李盛涛,王辉,林春江,李建英2013物理学报62 087701]

[64]Pathmanathan K,Stevens J R 1990J.Appl.Phys.68 5128

[65]Davidson D W 1961Can.J.Chem.39 571

[66]Zhao X T,Li J Y,Li H,Li S T 2012J.Appl.Phys.111 124106

[67]Gupta T K,Carlson W G,Hower P L 1981J.Appl.Phys.52 4104

[68]Chen Z X,Lin G C,Fu G A 1998Sci.China Ser.A:Math.Phys.Astron.41 71

[69]Sinclair D C,West A R 1989J.Appl.Phys.66 3850

[70]Al Abdullah K,Bui A,Loubiere A 1991J.Appl.Phys.69 4046

PACS:77.22.Gm,73.30.+y,73.40.Qv,77.84.Cg DOI:10.7498/aps.66.027701

Recent research progress of relaxation performances of defects in ZnO-Bi2O3varistor ceamics∗

Zhao Xiao-Qiang1)2)Zhao Xue-Tong1)†Xu Chao1)Li Wei-Wei3)Ren Lu-Lu1)Liao Rui-Jin1)Li Jian-Ying4)

1)(State Key Laboratory of Power Transmission Equipment and System Security and New Technology,College of Electrical Engineering,Chongqing University,Chongqing 400044,China)
2)(College of Computer Science,Chongqing University,Chongqing 400044,China)
3)(State Grid Sichuan Electric Power Research Institute,Chengdu 610072,China)
4)(State Key Laboratory of Electrical Insulation and Power Equipment,College of Electrical Engineering,Xi’an Jiaotong
University,Xi’an 710049,China)

6 October 2016;revised manuscript

1 November 2016)

ZnO varistor ceramics have been widely applied to surge absorption and over-voltage protection in electronic circuit and power system because of their excellent non-ohmic characteristics.Therefore,the reaserch on ZnO varistor ceramic has long been a subject of interest for scholars and industrial circles.At present,the conductance theory of ZnO varistor ceramic has been widely studied and reviewed,and several models such as space charge limited current model,Nordheim-Fowler tunneling current model,and Schottky barrier model have been proposed to describe the electronic transmission process and explain the non-ohmic behavior of ZnO ceramic varistor.However,the relationships of the defect structure and defect relaxation with the electrical property of ZnO varistor ceramic remain unclear,which becomes a challenge to developing new ZnO varistor ceramics.In this paper,comments on defect structures and defect types of ZnO ceramics are given,and the theortical calculation of the intrinsic point defects is discussed.Besides,the characterization technologies of the defect relaxations are introduced.The results show that the dielectric loss spectra are widely used to describe the relaxation of ZnO ceramic varistor,especially the spectra in the low frequency can provide more information about defect relaxation of ZnO ceramic varistor.It is also found that the frequency spectra of admittance in a wide temperature range and the temperature spectra of admittance in a wide frequency range play an equivalent role in characterizing the defect relaxation of ZnO ceramic varistor.The thermally stimulated current is considered to be an effective method to verify the relaxation polarization mechanism of the defects.The deep level transient spectroscopy can characterize the intrinsic and extrinsic defect relaxation processes.Moreover,several theories of relaxation mechanisms such as the Cole-Cole theory,Havriliak-Negami theory and Cole-Davidson theory are proposed to analyze the relaxation phenomena of ZnO ceramic varistors.It is suggested that the electric modulus spectrum combined with Cole-Davidson theory is more effective to characterize the defect relaxations in a wide temperature range.From the electrical degradation results,it is found that the extrinsic defect relaxation at grain boundary interface is closely related to the electrical property of ZnO ceramic varistor.A circuit model is also obtained to establish the correlation between defect relaxation and electrical performance of ZnO ceramic varistor.Therefore,the review on defect relaxations may offer some new ideas to optimize the electrical properties of ZnO ceramic varistors by modifying the defect structures.

ZnO varistor ceramics,defect structures,relaxation mechanism,electrical properties

:77.22.Gm,73.30.+y,73.40.Qv,77.84.Cg

10.7498/aps.66.027701

∗国家自然科学基金青年科学基金(批准号：51407019)、中央高校基本科研业务费(批准号：106112015CDJZR155509)和输变电装备及系统安全与新技术国家重点实验室培育基金(批准号：2007DA10512716302)资助的课题.

†通信作者.E-mail：zxt201314@cqu.edu.cn

*Project supported the Young Scientists Fund of the National Natural Science Foundation of China(Grant No.51407019),the Fundamental Research Fund for the Central Universities,China(Grant No.106112015CDJZR155509),and the Research Fund from the State Key Laboratory of Power Transmission Equipment&System Security and New Technology,China(Grant No.2007DA10512716302).

†Corresponding author.E-mail：zxt201314@cqu.edu.cn