基于分段信号相关累加的变速度多站联合直接定位方法∗

逯志宇任衍青 巴斌 王大鸣 张杰

1)(解放军信息工程大学,郑州 450000)

2)(解放军66159部队,武汉 430000)

基于分段信号相关累加的变速度多站联合直接定位方法∗

逯志宇1)†任衍青1)巴斌1)王大鸣1)张杰2)

1)(解放军信息工程大学,郑州 450000)

2)(解放军66159部队,武汉 430000)

(2016年7月26日收到;2016年11月3日收到修改稿)

在低信噪比条件下,基于时延和多普勒频移的直接定位算法在解决宽带信号源定位时精度较差.针对此问题,提出了一种基于分段信号相关累加的变速度多站联合直接定位算法,并给出了其克拉美罗下界.该算法利用多个变速度的观测站对信号进行接收,然后将同一观测站接收的目标信号分割成多段不重叠的短时信号,采用最大似然估计器,联合各段信号的时延、多普勒频移信息对目标进行直接定位.算法充分利用了观测信号包含的定位信息,并利用观测站速度的变化增加了目标位置信息,解决了分段信号联合估计带来的定位模糊问题,使定位精度进一步提高,增加了算法的实用性.仿真实验表明,较之传统直接定位算法,本文算法定位精度更高,尤其在低信噪比条件下更能逼近克拉美罗界.

直接定位,多普勒频移,最大似然,克拉美罗界

1 引 言

无线目标定位技术不论是在民用领域还是军事领域,都具有广泛的应用空间,为了满足各种环境下的定位需求,定位算法得到快速发展,其中以传统两步定位算法取得的成果最为显著.两步定位算法首先需要对目标信号的到达时间(TOA)[1],到达方向(DOA)[2]和到达时间差(TDOA)[3,4]等位置参数进行估计,然后对定位方程求解获得目标位置.大量文献已表明,在高信噪比条件下两步定位方法具有一定应用价值[5-7].但是,这种两步定位方法忽略了观测站之间定位参数的内在关系,第一步获得的参数与第二步的位置估计缺乏联系,导致位置信息丢失,同时在分步计算中不可避免地引入了处理误差,所以两步定位方法是次优的,不能获得最佳的定位性能[8].与之相比,近年来被提出的直接定位(DPD)算法不需要参数估计和位置解算分步计算,而是基于最大似然准则,在接收信号中直接进行位置估计,避免了位置信息的损失,定位性能更优,成为研究热点[9-15].文献[9]首次对DPD算法进行了系统分析,给出了窄带系统下单目标定位算法,证明其相比于两步定位算法性能更优,尤其是在低信噪比条件下能够逼近克拉美罗下界(CRLB).为了进一步挖掘DPD算法优势,文献[10-15]给出了多种改进型算法,融合了TOA,到达角(AOA),DOA和TDOA等多种参数进行联合直接定位,性能优越.虽然DPD算法计算量较高,但在快速发展的云计算技术[16,17]以及各种智能算法[18-20]的支撑下,其应用前景较为广泛.

随着机载、舰载、车载等运动观测平台的大量应用,以及信号带宽的扩大,研究宽带条件下的运动观测站直接定位技术变得尤为重要.本文主要讨论观测站运动条件下的宽带信号源定位问题.为了使窄带定位算法在宽带条件下仍能发挥作用,通常做法是将接收信号划分为多段短时信号,然后联合短时信号包含的位置信息进行定位.文献[21]给出了一种用于窄带信号源的DPD算法,基于运动观测平台获得的多普勒信息进行定位,性能相对于传统两步定位算法有较大提高.在此基础上,文献[22]给出了一种面向宽带信号源,利用分段短时信号累加技术的DPD算法,提高了目标定位精度.但算法采用非相关累加方法,忽略了短时信号之间的相关性,目标位置信息仍有一定损失.为了进一步提高宽带信号源的定位精度,分段短时信号之间的相关性应该被考虑.基于相关处理的DPD算法也得到了一些研究,如文献[23]基于阵列模型给出了时频域下的相关和非相关处理流程,证明了相关处理的性能优势.文献[24]进一步分析了无源定位环境下的相关累加DPD算法性能.文献[25]推导了多个相位同步的静态雷达对目标进行直接定位的CRLB.上述研究工作对相关处理DPD算法的分析做出较大贡献,但是仍面临两个主要问题,一是没有考虑同一观测站的短时信号之间的相关性信息;二是接收站和目标之间需要相位同步,这在实际应用中较难满足.为了解决这两个问题,文献[26]提出了一种利用同一观测站短时信号相关累加的DPD算法,并且解决了观测站和目标之间的相位同步误差问题,使算法更具实用价值.但是多段接收信号相关性信息的引入,带来2π模糊问题,会使定位结果存在多解,导致算法必须将传统DPD算法的估计结果作为初始估计,定位精度受初值估计精度限制,尤其在低信噪比条件下,算法性能并没有显著的提升.

综上所述,现有算法在解决运动观测平台下的宽带信号源定位问题时,仍有一定不足.分段短时信号相关性信息的利用已被证实能够提高定位性能,但是其带来的多解问题又制约了性能的突破,尤其是在信噪比较低时失去了实际意义.因此,如何利用相关性信息中包含的位置信息提高定位精度,同时又避免多解问题,具有重要研究价值.针对此研究目标,本文在文献[26]基础上,提出了一种基于分段信号相关累加的变速度多站联合直接定位算法(variable velocity receivers for DPD based on correlation accumulation of short-time signals,VC-DPD),与现有算法相比,所提算法充分利用分段短时信号相关性信息的同时,通过速度多变性增加了目标的位置信息,从而解决了定位模糊问题,使算法不再依赖非相关DPD算法的初始估计,在低信噪比条件下也能接近CRLB下界,更具实用价值.本文首先给出了变速度多站联合直接定位模型,然后对算法进行了理论分析,推导了算法的CRLB,最后通过仿真实验证明了算法的有效性.

2 变速度多站联合定位模型

假设目标处于静止状态,坐标为o=(ox,oy).观测站个数为L,且已经完成时间同步.观测站以间隔T0对目标信号进行接收,共获得K段观测信号.每次观测的起始时间为tk,k=1,2,···,K,持续时间为T,观测站坐标为ul,k=(ux,uy),l=1,2,···,L,速度为˙ul,k=(˙ux,˙uy),且满足

即观测站在不同的观测时间段Km内速度不同,但在每段时间内恒定为˙um.定位模型如图1所示.

图1 直接定位场景Fig.1.DPD Scenario.

假设目标发送信号为

其中fc是载频,φ是初始相位,s(t)是信号的包络.第l个观测站在第k个时隙内接收到的信号为

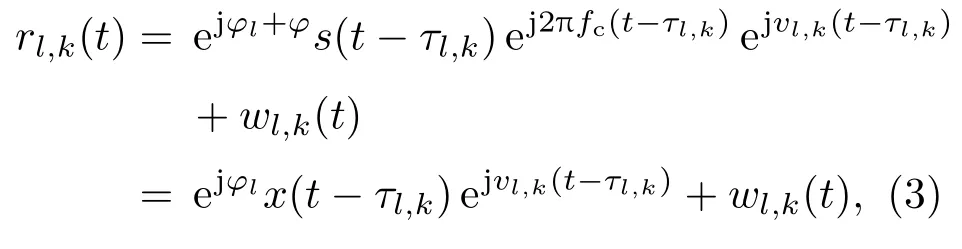
其中φl表示观测站和目标之间的相位差,wl,k(t)为高斯白噪声,服从C(0,σl,k)分布.τl,k和vl,k分别是接收信号的时延和多普勒频移：

观测信号的离散表示为

其中采样间隔为Ts,每个观测时隙内取Nk个样本点,ntk=tk/Ts为起始观测时刻,nτl,k=τl,k/Ts为时延的离散表示,nvl,k=vl,kTs为多普勒频移的离散表示. 令x[nk-nτl,k]=x(ntk+nkT-nτl,k),rl,k[nk]=rl,k(ntk+nkT),则(6)式可表示为

DPD算法即通过(7)式中的接收信号进行直接位置估计.文献[22,23]为了简化运算,忽略了公式中项,损失了一部分位置信息.文献[26]虽然利用这部分信息提高了定位精度,但是没有解决的引入带来的定位模糊问题.在本文接下来要讨论的算法中,将对这部分信息进行利用,并着力解决定位模糊问题,在提高精度的同时,使算法更具实用价值.

为充分利用所有观测信号,下面首先将观测信号进行联合表示.令

由文献[27],x[nk-nτl,k]可以表示为

其中

表示离散傅里叶变换(DFT)矩阵,

表示时延矩阵.令

其中1Nk表示Nk×1的全1向量,INk表示Nk×Nk的单位矩阵.联合(8)式-(10)式,可将接收信号表示为

其中

由于不同观测时间段内速度不同,将接收信号根据速度变化进行分段表示,用rl,m,km代替rl,k,可将(11)式改写为

其中m=1,2,···,M,km=Km-1+1,···,Km,令

进一步可得

根据(15)式,可将所有观测站的接收信号联合表示为

其中

3 面向宽带信号源的VC-DPD定位方法

在第二节给出的定位模型下,本节将对VCDPD算法的原理进行推导,给出未知信号条件下的目标位置最大似然估计公式,在理论上证明算法的可行性.在无源定位系统中,未知参数包括信号x,相位误差φl,目标位置o,定义待估计量为η,表示为

其中θ由目标位置和相位误差组成,表示为

从(16)式可以看出,接收信号r是以Hx为均值,Γ为协方差矩阵的复高斯变量,可将其概率密度函数表示为

根据最大似然准则,θ的估计可由下式给出

找到目标函数f(θ)的最大值,即为θ的估计.

根据Hm,km的定义,可以得到：

当目标发射信号未知时,xm,km的最大似然估计可表示为[26]

根据(18)式,θ由相位偏差φl,l=1,···,L和目标位置o组成,要通过(24)式得到目标的位置估计,需要进行高维联合搜索.当L较大时,搜索计算量大,严重影响算法的实用价值.因此需设计合理算法去除φl的影响.将代入(24)式,可以得到

根据(26)式,在目标可能存在的区域进行网格搜索,即获得位置的最终估计.ejvl,k(t-τl,k)中位置信息带来的定位模糊问题与速度成对应关系,所以在不同速度条件下,真实位置相同,而模糊解位置不同.本文提出的变速度多站观测模型正是利用这一特点,消除了模糊解.从(26)式可以看出,通过观测速度的分段变化,可以使真实位置的函数值叠加而不断增大,而各段内模糊位置的函数值不再叠加,变得分散,从而能与真实值位置区分开.所以算法不再需要非相关DPD算法提供一个粗略的初始位置,而又充分利用了观测信号中包含的位置信息,定位性能得到保证,仿真部分将进一步证明算法的有效性.

为了更加清晰地展现算法架构,基于本节对算法原理的推导和分析,可以将本文算法的流程总结为：

1)在目标可能存在的区域内划分合理的网格节点：o1,o2,···,og,令i=1;

5)计算

6)如果i＜g,令i=i+1,跳转到步骤2;

7)找到令U值最大的点max,即为目标位置的估计值.

4 克拉美罗界

为了进一步给出算法定位性能,本节将对所提算法的克拉美罗界进行推导.根据(19)式,未知向量η可以表示为

根据文献[25,26],其费希尔信息矩阵(FIM)可以表示为

根据(18)式中θ的定义,可以得到

根据(12)式,有

联合(28)式-(37)式,Jη可以表示为

其中

根据分块矩阵的求逆公式[22],θ的FIM矩阵可以表示为

取CRLBθ中表示目标位置估计误差的部分,即可得到位置估计的CRLBo.

5 仿真分析

为了验证所提算法的性能,本节将对算法的定位精度和CRLB进行仿真.在利用时延和多普勒频移信息的直接定位算法中,文献[22]提出的非相关DPD算法(下称NC-DPD)和文献[26]提出的相关DPD算法(下称C-DPD)具有代表性,因此仿真结果主要与这两篇文献进行对比.假设目标位于一个二维平面内,坐标为o=(0,0).观测站个数L=3,观测次数K=20,速度变化一次,即M=2,K1=10,K2=10,各站具体参数如表1所列.

表1 观测站参数设置Table 1.Theparameters of receivers.

图2 (网刊彩色)不同算法的定位结果对比 (a)3D NC-DPD;(b)3D NC-DPD;(c)3D C-DPD;(d)2D C-DPD;(e)3D VC-DPD;(f)2D VC-DPDFig.2.(color online)Evaluation of the cost functions of the source location estimators foreach algorithm：(a)3D NC-DPD;(b)3D NC-DPD;(c)3D C-DPD;(d)2D C-DPD;(e)3D VC-DPD;(f)2D VC-DPD.

目标发送信号采用随机高斯信号模型,载波频率fc=300 MHz,采样频率为fs=50 kHz,观测间隔T0=0.1 s,每次采样时间为T=1 ms,采样点数为Nk=50,搜索区间为[-1000,1000]m,NCDPD和C-DPD算法中各观测站采用速度˙u1恒定不变.

为了清晰地对比不同算法的定位性能,在信噪比20 dB条件下,我们在搜索区间内以1 m为间隔,分别计算不同算法的目标函数值,结果如图2所示.为了更好地说明算法性能,分别给出了仿真结果的立体和平面效果图,其中图2(a)和图2(b)是NC-DPD算法的仿真结果,图2(c)和图2(d)是C-DPD算法的仿真结果,图2(e)和图2(f)是VCDPD算法的仿真结果.

从图2(a)和图2(b)可以看出,虽然信噪比已经很高,但NC-DPD算法的目标函数值在真实位置附近仍形成了一个较大的模糊区域,要得到高精度的位置估计较为困难,一旦信噪比下降,定位性能会快速下降.从图2(c)和图2(d)可以看出,C-DPD算法在目标真实位置形成了较为尖锐的峰,相比于NC-DPD算法,估计精度得到了提升.形成这种结果的原因在于算法引入了分段信号间的相关性信息,增加了目标位置信息,定位精度有所提升.但从图中也可以看到,定位结果存在多解,影响算法实用价值.从图2(e)和图2(f)可以看出,本文提出的VC-DPD算法在充分利用分段信号相关性信息条件下,仍能够得到惟一的高精度的定位结果,解决了C-DPD算法的定位模糊问题,与理论推导相符合.

为了进一步说明VC-DPD算法的定位性能,对比不同算法的CRLB和估计误差随信噪比的变化趋势,对各算法进行200次蒙特卡罗仿真实验,结果如图3所示.从图中可以看出,随着信噪比的提高,各算法性能都有所提升.但在高信噪比条件下,本文算法性能略好于C-DPD算法,精度有大概3 dB的提升,而相比于NC-DPD算法精度至少提高20 dB;在低信噪比条件下,本文算法仍然具有极好的性能,估计误差始终接近其CRLB,而NC-DPD算法性能快速下降,由于C-DPD算法以NC-DPD算法的估计结果作为初值,其性能也随之迅速变差,与其CRLB相差甚远.

图3 (网刊彩色)不同算法性能随信噪比变化趋势Fig.3.(color online)Estimation accuracy of each algorithm as a function of SNR.

图4 (网刊彩色)不同算法性能随观测间隔T0变化趋势Fig.4.(color online)Estimation accuracy of each algorithm as a function ofT0.

为了验证观测时间间隔T0对算法性能的影响,在信噪比SNR=10 dB,观测次数K=20条件下,图4给出不同算法性能随T0的变化趋势.从图中可以看出,VC-DPD和C-DPD算法的CRLB会随着观测时间间隔的变大而减小,性能越来越好.而NC-DPD算法的性能不会随观测时间间隔的变化而改变.另外,从定位均方误差中可以看出,VC-DPD算法能够贴近其CRLB,具有较好的估计性能.而C-DPD算法尽管CRLB比较低,但是估计误差与NC-DPD算法一致,随着观测间隔的变大并没有变好.这是C-DPD算法将NC-DPD算法的估计结果作为初始值带来的最大问题,即在低信噪比条件下,随着时间间隔的扩大,在NC-DPD算法性能没有提升条件下,C-DPD算法性能也不会得到提升.

为了验证不同算法性能随观测次数K的变化趋势,在信噪比SNR=10 dB,观测时间间隔T0=0.1 s条件下,图5给出了不同算法性能的仿真结果.可以看出,随着观测次数的增加,各算法性能都有提升,但NC-DPD算法性能提升有限,而VC-DPD和C-DPD算法提升较为明显.和前面仿真得到的结论一样,C-DPD算法受NC-DPD算法影响,即使在K很大时也无法获得较好的估计性能,而VC-DPD算法不受此约束,估计性能较优.同时还可以看到,本文算法在观测次数较少时仍具有较好的性能,在一定程度上提高了定位效率,保证了算法的时效性.

图5 (网刊彩色)不同算法性能随观测次数K变化趋势Fig.5.(color online)Estimation accuracy of each algorithm asa function ofK.

从以上仿真结果可以看出,由于本文提出的VC-DPD算法不受NC-DPD算法约束,在低信噪比条件下具有优良的性能.相比于C-DPD算法,既利用了多段信号之间的相关性信息提高了定位精度,又解决了多解问题,使算法更具实用价值.在相同环境条件下,本文算法在较少观测次数条件下即能获得较好的估计结果,定位时效性得到了保证.

6 结 论

针对低信噪比条件下,现有直接定位算法在时延和多普勒频移联合定位中精度不高的问题,本文提出了一种基于速度动态变化的直接定位算法,给出了详细的模型构建、原理分析和CRLB推导过程.算法联合时延、多普勒频移以及多段信号之间的相关性信息进行直接定位,在充分挖掘接收信号包含的目标位置信息的同时,解决了定位模糊问题,进一步提高了定位精度.仿真实验给出了所提算法与其他算法的性能对比,证明了算法在低信噪比条件下能够获得更好的定位性能,具有一定的实用价值.

[1]Oh D,Kim S,Yoon S H 2013IEEE Trans.Wireless Commun.12 3130

[2]Lei H,So H C 2013IEEE Trans.Signal Process.61 4860

[3]Ba B,Liu G C,Li T,Lin Y C,Wang Y 2015Acta Phys.Sin.64 078403(in Chinese)[巴斌,刘国春,李韬,林禹丞,王瑜2015物理学报64 078403]

[4]Lu Z Y,Wang D M,Wang J H,Wang Y 2015Acta Phys.Sin.64 150502(in Chinese)[逯志宇,王大鸣,王建辉,王跃2015物理学报64 150502]

[5]Wang G,Li Y M,Nirwan A 2013IEEE Trans.Veh.Technol.62 853

[6]Ho K C,Chan Y T 1997IEEE Trans.Aerosp.Electron.Syst.33 770

[7]Chan Y T,Ho K C 2005IEEE Trans.Signal Process.53 2625

[8]Bosse J,Ferréol A,Larzabal P 2011IEEE Statistical Signal Processing WorkshopNice,France,June 2-6,2011 p701

[9]Weiss A J 2004IEEE Signal Process Lett.11 513

[10]Weiss A J,Amar A 2005EURASIP J.Adv.Signal Process.1 37

[11]Amar A,Weiss A J 2006Digital Signal Process.16 52

[12]Bar-Shalom O,Weiss A J 2011Signal Process.91 2345

[13]Pourhomayoun M,Fowler M L 2014IEEE Trans.Aerosp.Electron.Syst.50 2878

[14]Vankayalapati N,Kay S,Ding Q 2014IEEE Trans.Aerosp.Electron.Syst.50 1616

[15]Tirer T,Weiss A J 2016IEEE Signal Process Lett.23 192

[16]Fu Z J,Sun X M,Liu Q,Zhou L,Shu J G 2015IEICE Trans.Commun.98 190

[17]Ren Y J,Shen J,Wang J,Han J,Lee S Y 2015J.Internet Technol.16 317

[18]Gu B,Sheng V S,Wang Z J,Ho D,Osman S,Li S 2015Neural Networks67 140

[19]Wen X Z,Shao L,Xue Y,Fang W 2015Inform.Sci.295 395

[20]Xie S D,Wang Y X 2014Wireless Pers.Commun.78 231

[21]Amar A,Weiss A J 2008IEEE Trans.Signal Process.56 5500

[22]Weiss A J 2011IEEE Trans.Signal Process.59 2513

[23]Oispuu M,Nickel U 2010International Itg Workshop on Smart Antennas IEEE1 300

[24]Bosse J,Ferreol A,Larzabal P 2013IEEE Trans.Signal Process.61 5485

[25]Godrich H,Haimovich A M,Blum R S 2010Information Theory IEEE Transactions on56 2783

[26]Li J Z,Yang L,Guo F C,Jiang W L 2015Digital Signal Process.48 58

[27]Yeredor A,Angel E 2011IEEE Trans.Signal Process.59 1612

PACS:05.45.Tp,05.40.-a DOI:10.7498/aps.66.020503

An improved direct position determination method based on correlation accumulation of short-time signals with variable velocity receivers∗

Lu Zhi-Yu1)†Ren Yan-Qing1)Ba Bin1)Wang Da-Ming1)Zhang Jie2)

1)(PLA Information Engineering University,Zhengzhou 450000,China)
2)(The 66159thUnit of PLA,Wuhan 430000,China)

26 July 2016;revised manuscript

3 November 2016)

Wireless target location technology has been widely used in civil and military fields.In the two-step localization algorithms,the signal measurements,such as thetime of arrival,theangle of arrival,the frequency difference of arrival,etc.,should be extracted first from the receivedsource signal.Then the target position is identified by calculating the location equation.Compared with the two-step localization algorithms,the direct position determination(DPD)method,which need not estimate the signal parameters and calculate the position step by step,but obtainsthe source position from the received signals directly based on the maximum likelihood criterion,has been shown to have a goodestimation accuracy and robustness,especially under low signal-to-noise ratio(SNR)conditions.So it has been widely studied in recent years and has made remarkable achievements in academic research.However,the DPD algorithm of wideband signals emitters is not performing well with moving receivers in the joint positioning based on time delay and Doppler shift under the low SNRs.To obtaina better positioning performance,in this paper we present a DPD algorithm with variable velocity receivers based on coherent summation of short-time signal segments,and derive the source position Cramer-Rao lower bound(CRLB).The algorithm designs a positioning model in which the multiple variable velocity receivers are usedtoobtain the source signal,then the signal received at the same receiver is patitioned into multiple non-overlapping short-time signal segments,based on which,an approximate maximum likelihood estimator for the new DPD algorithm is developed.The algorithm makes full use of the location information contained in the coherency among the signals segments,while extra target position information is acquired through the speed variability in the positioning model,and thus the problem of location ambiguity is solved.The simulation results show thatthe algorithm proposed in this paper further improves the positioning performance,and outperforms the traditional DPD algorithms with more accurate results.Especially in the low SNR,it is closer to the CRLB.

direct position determination,dopplershift,maximum likelihood,Cramer-Rao lower bound

:05.45.Tp,05.40.-a

10.7498/aps.66.020503

∗国家高技术研究发展计划(批准号：2012AA01A502,2012AA01A505)和国家自然科学基金(批准号：61401513)资助的课题.

†通信作者.E-mail：zhiyulu1030@126.com

*Project supported by the National High Technology Research and Development Program of China(Grant Nos.2012AA01A502,2012AA01A505)and the National Natural Science Foundation of China(Grant No.61401513).

†Corresponding author.E-mail：zhiyulu1030@126.com