静电场作用下电介质电热效应的热力学机理*
2017-08-01韩光泽邢倩
韩光泽 邢倩
(华南理工大学 物理系, 广东 广州 510640)
静电场作用下电介质电热效应的热力学机理*
韩光泽 邢倩
(华南理工大学 物理系, 广东 广州 510640)
以电热效应为基础的固体制冷技术在微电子器件散热等方面有重要的应用.文中将极化能引入热力学基本微分方程,导出了静电场作用下系统的热容、温度、熵和热流量等随外场变化的计算公式,并选用钛酸钡的实验数据验证热力学理论公式,发现这些热力学理论计算式与文献资料提供的实验结果相符.研究表明,电偶极矩随外界温度发生变化是产生电热效应的基础,且介电常数的温度变化率越大,电热效应越明显,因此巨电热效应的研究方向应该是寻找介电常数随温度的剧烈变化区域.
电介质;电热效应;热力学;静电场;钛酸钡
电介质的电热效应是指在静电场作用下电介质的热容、温度和热流量等宏观热力学量发生变化的现象.电热效应有许多重要的应用,例如可以利用电场作用下的电热效应强化对流传热过程[1],也可以利用电场作用下电介质温度的变化来设计和制造制冷器件[2],这也是其目前得到广泛关注的原因[3].此外,由于具有固态、可小型化、无损耗、不需要流动制冷剂和转动机械设备等优点,以电介质电热效应为基础的固态制冷技术可用于微电子器件及微电机系统的散热.
通常情况下,电介质材料的电热效应都很微弱,达不到实际应用的标准,因此寻找具有巨电热效应的材料就成了目前的研究主流,且以实验研究为主[4- 9].然而,静电场作用下电介质的电热效应不同于交变电场作用下的热效应.交变电场作用下的热效应是电介质分子随交变电场转动时,由于弛豫摩擦而生热,本质上是电变热的不可逆过程;静电场作用下电介质的电热效应本质上是电介质中的电偶极子在电场作用下做有序排列,这种有序化排列改变了电介质的熵和内能等热力学特征量,进而引起热容、温度和热流量等宏观量的变化,这是一个宏观的可逆过程.
热力学是关于热运动的宏观理论,它以4个基本定律为基础,应用数学方法,通过逻辑演绎得出物质各种宏观性质之间的关系,具有高度的可靠性和普遍性,因此热力学是揭示电热效应的最有效理论之一.文中利用外场作用下的普遍化热力学理论揭示静电场作用下电介质电热效应的热力学机理,并利用文献实验数据验证相关的理论描述,以期加深对电介质电热现象的理解,为相关的实验研究提供理论参考.
1 电介质电场热效应的热力学机理
1.1 外场作用下的基本热力学微分关系
设在某一微小过程中,系统从外界吸收了热量δQ,同时外界对系统做的各种形式的功是∑δW,则系统的热力学能U可以由热力学第一定律普遍地表示为
dU=δQ+∑δW
(1)
由热力学第二定律可知,在任何可逆过程中系统吸收的热量与系统的熵S和温度T之间有关系式δQ=TdS.能量公理表明[10- 11],能量的微分可以普遍地表示为XjdYj,Xj和Yj分别表示第j种形式的强度量和广延量,Xj可以理解为第j种形式的场量.由于能量的传递过程是通过做功来实现的,因此也可以说XjdYj是外界对系统做的功.设除热量交换外,系统还可以通过多种形式的功与外界进行能量交换.因此,当有多种外场作用于多组分热力学系统时,依据热力学第一定律,系统热力学能的微分可以普遍化地表示为[12- 13]
dU=TdS-pdV+∑μidni+∑XjdYj
(2)
式(2)中的p和V分别表示系统的压强和体积,μi和ni分别表示第i种物质的化学势和物质的量.
电介质在外电场E作用下发生极化,极化效果用极化强度P表示,即单位体积电介质的电偶极矩.电偶极矩反映了电介质系统对外电场的响应,也是外加电场对电介质作用的宏观体现.对于均匀极化的电介质系统,总电偶极矩可表示为P′=PV.电介质极化的实质是获得极化能,极化能的微分(也可以说是电场对介质做的极化功)是dWp=E·dP′,在各向同性的电介质中可简化为dWp=EdP′[14].因此,电场作用下电介质系统的热力学能微分式为
dU=TdS-pdV+∑μidni+EdP′
(3)
这就是电介质系统的基本微分关系式.为了能够方便地导出热力学量间的微分关系,再定义电场作用下电介质系统的吉布斯函数Ge:
Ge=U-TS+pV-EP′
(4)
利用热力学能的微分式(3),可得到该吉布斯函数的全微分:
dGe=-SdT+Vdp+∑μidni-P′dE
(5)
任意二元函数z=z(x,y)的全微分是dz(x,y)=(∂z/∂x)dx+(∂z/∂y)dy.全微分条件表明,函数的二阶混合偏导数与求导顺序无关,即(∂2z/∂x∂y)=(∂2z/∂y∂x).利用这个全微分条件,可以从吉布斯函数的微分式(5)中导出偏微分方程:
(6)
1.2 静电场作用下电介质的热容
对于没有化学反应及与外界没有物质交换的封闭系统,dni=0.利用可逆过程中的关系式δQ=TdS和基本微分式(3),可将电场作用下电介质的定容热容和定压热容分别表示为
(7)
(8)
对于凝聚相电介质(尤其是固相),通常情况下其密度ρ随外界条件变化很小,可以近似为常数.此时定容过程与定压过程没有差别,质量热容可表示为
(9)
这就是电场作用下电介质的热容.该式表明,电场对热容的影响取决于极化强度对温度的变化率.随着温度上升,分子振动加剧,偶极分子的排列通常趋于无序,极化强度减小,该变化率为负值.也就是说,通常情况下电场作用使电介质的热容增大.热能(也称内能)是组成物质微观粒子无规则机械运动的动能,取向极化能是电偶极子沿电场方向排列的势能.电场作用下电介质从外界吸收的热量一部分用于增加粒子的机械运动,一部分用于打乱电偶极子的规则排列,因此在升高相同的温度时,需要吸收更多的热量,这就是电场作用使热容增加的物理机制.
1.3 静电场作用下电介质的温度
吉布斯函数是与物质的量相关的广延量,微分式(5)表明,系统的广延量可以表示为系统的温度、压强、物质的量和电场强度为自变量的函数,Ge=Ge(T,p,ni,E).系统的熵也是广延量,因此也可以表示为S=S(T,p,ni,E),所以有微分式
(10)
对于没有化学反应及与外界没有物质交换的封闭系统(dni=0),在等压、绝热条件下(dp=dS=0),利用热容式(8)及偏导数关系式(6),可由式(10)得
(11)
或
(12)
对凝聚相电介质,对上式积分得
(13)
这就是绝热条件下电介质系统的温度随外加电场的变化关系.
1.4 电场作用引起的熵变及热流量
偏导数关系式(6)反映了电介质系统的熵随电场的变化率,对该式积分可得
(14)
对凝聚相电介质,可表示为单位质量比熵:
(15)
这就是电场作用引起的电介质熵变化.
电场作用可以引起电介质内能的变化,在绝热条件下表现为电介质温度的变化,在等温条件下电场作用必然会引起电介质吸(放)热.等温过程中电场作用引起的单位质量电介质与外界交换的热量为
(16)
这就是等温条件下电场作用引起的电介质吸热量(或放热量).
2 验证及讨论
钛酸钡是一种应用非常广泛的铁电体材料[15].由于具有优良的电热性质,目前关于钛酸钡的实验研究较多,文献中有较丰富的实验资料,因此文中选用钛酸钡的实验资料验证热力学理论公式.由于实验方法、测试手段以及钛酸钡样品等方面的差异,文献给出的测量值存在较大的差别,有些甚至不相容.只有来自同一组实验的测量值才有定量计算、相互印证的意义,因此选用文献[4-5]中数据进行分析.
2.1 电介质的热容
Nikola等[4- 5]在沿[001]空间结构方向厚度为390 μm的钛酸钡单晶片的两个表面涂上金属银作为电极,通过施加大小为10 kV/cm、频率为1 kHz的电场测量了钛酸钡的复介电常数随温度的变化.介电常数的实部ε如图1(a)所示,电场作用下钛酸钡在412 K左右发生相变.图1(a)显示出,介电常数在360 K左右的铁电相随温度缓慢增加,对温度的变化率为正;介电常数在高于412 K的顺电相随温度急剧减小,对温度的变化率为负值.Nikola等[4- 5]还同时测量了没有电场和有电场作用时钛酸钡的热容,如图1(b)和1(c)所示.对比图1(b)和1(c)可发现:在温度低于412 K的铁电相,电场作用使钛酸钡的热容减小;而在高于412 K的顺电相,电场作用使热容增大.
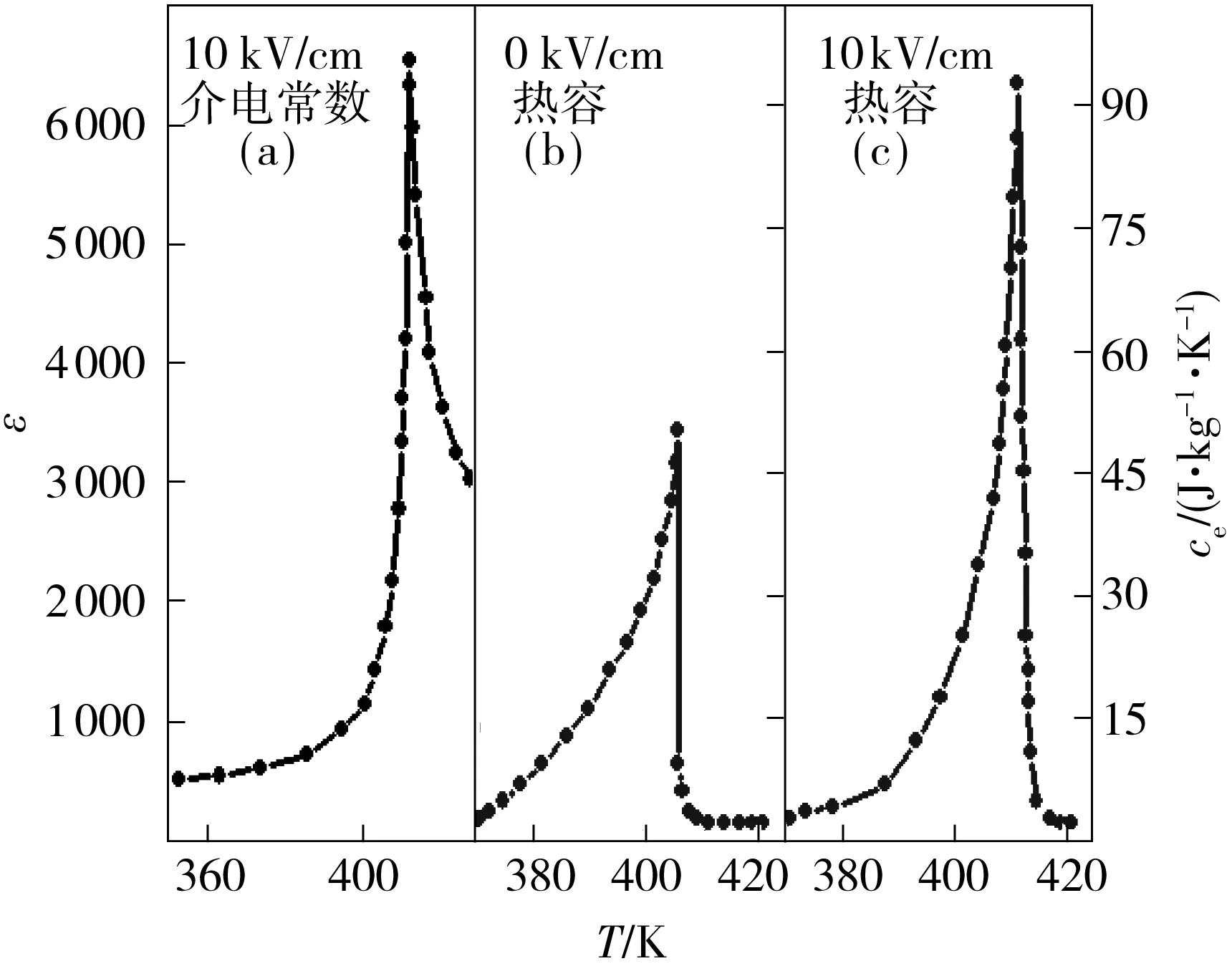
图1 钛酸钡的介电常数、热容随温度的变化[4- 5]
Fig.1 Changes of dielectric constant and heat capacity of barium titanate with temperature[4- 5]
图1给出的有关热容的实验资料完全符合公式(9)的预测.由德拜方程可知,低频条件下,复介电常数的实部近似等于静态介电常数.极化强度与外加电场的关系是P=ε0(ε-1)E.因此极化强度随温度的变化率正比于介电常数随温度的变化率,(∂P/∂T)E=ε0E(∂ε/∂T)E.式(9)可改写为
(17)
c0为无电场时的质量热容,ε0为真空中的介电常数.在温度低于412 K的铁电相,由于(∂ε/∂T)E>0,所以ce
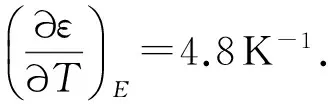
2.2 电介质的温度
在文献[6]中,Kar-Narayan利用电容器中填充多层掺杂钛酸钡的方法,测量了掺杂钛酸钡的电位移随温度的变化,见图2.在电场强度E=3.0×107V/m不变的情况下,钛酸钡的电位移(D)近似随温度线性减小.对实验点做线性拟合后得(∂D/∂T)E=-1.5×10-4C/(m2·K).由于电场不随温度变化,由关系式D=ε0E+P得(∂D/∂T)E=(∂P/∂T)E.该文献的实验表明,斜率(∂D/∂T)E随电场近似不变.电场引起的热容变化也很小.电场引起的温度变化也只有0.1%,即有ln(T/T0)≈(T-T0)/T0.其中,T0为无电场时的温度.因此电场作用引起钛酸钡的温度变化可近似由式(13)积分得
(18)
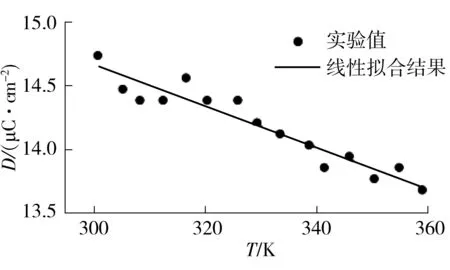
图2 钛酸钡的电位移随温度的变化[6]
Fig.2 Change in electric displacement of barium titanate with temperature[6]
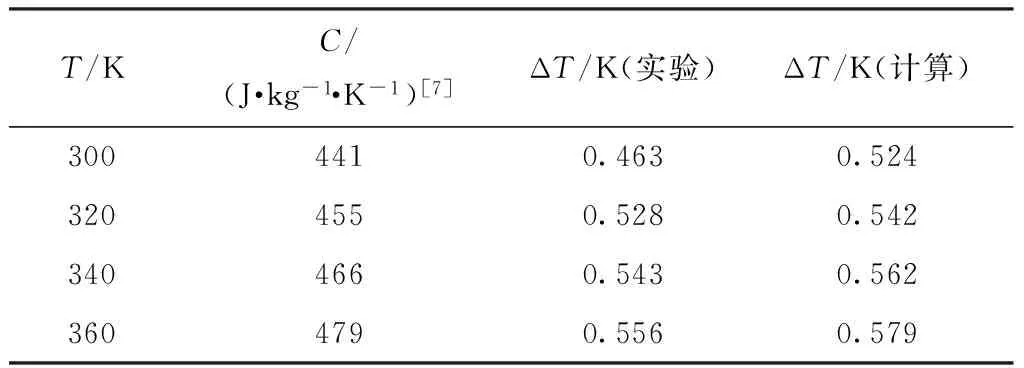
在文献[6]中,Kar-Narayan同时测量了在不同的温度点突然施加(或撤去)电场作用时引起的温度变化.结果表明,突然施加电场时温度突然上升,突然撤去电场时温度突然下降,实验值见表1.这一实验规律与式(18)相吻合.由于(∂D/∂T)E<0,所以由式(18)知ΔT与ΔE同正或同负,因此施加电场必然引起温度上升;反之,撤去电场温度必然下降.表1中的最右一列是利用式(18)计算的温度上升值,与实验测量值吻合.
表1 电场作用引起的钛酸钡温度上升值(300 kV/cm)
Table 1 Increases of temperature of barium titanate produced by applied electric field(300 kV/cm)
T/KC/(J·kg-1·K-1)[7]ΔT/K(实验)ΔT/K(计算)3004410.4630.5243204550.5280.5423404660.5430.5623604790.5560.579
2.3 电介质的熵和热流
Bai等[8- 9]利用流延成型方法,将粉体钛酸钡涂抹在基带上,再覆盖镍作为电极,焙烧后做成多层的(180层)测试样品,利用1 kHz的电场测量了样品的介电常数随温度的变化.在20~180 ℃、176 kV/cm电场作用下,测试样品的极化强度近似随温度线性减小,变化率(∂P/∂T)E约为-4.1×10-4C/(m2·K).忽略该变化率随电场的微小变化,对式(15)积分得质量比熵:
(19)
物质的熵是不能直接测量的物理量,它表示了样品中分子排列的有序程度;有序度越高,熵越小.由于(∂P/∂T)E<0,因此由式(19)得电场增加时Δs<0,也就是说电场作用使电介质的熵减小.这正是我们希望看到的结果,因为电场作用使电介质中的电偶极子沿电场方向有序排列,导致系统的有序程度增加,因而系统的熵减小.此外,图1(a)说明在相变点(412 K),介电常数对温度的斜率发生突变,由此导致熵的剧烈变化.这说明相变过程也就是电介质有序度发生突变的分子重排过程.
将式(19)代入式(16)可得等温条件下电场作用引起的热流量:
(20)
Bai等[8- 9]测量了等温条件下突然施加电场(或突然撤去电场)时钛酸钡样品的热流.实验发现:突然施加电场时样品放热,突然撤去电场时样品吸收等值的热量;在离开相变点的区域,电场不变时样品的放(吸)热量近似随温度线性增加,温度不变时样品的放(吸)热量近似随电场线性增加.这个实验结论与式(20)的预测完全相符.放热量和吸热量相等,说明电热效应是一个可逆过程,这正是制冷技术的基础.Bai等[8- 9]在176 kV/cm电场作用下,40 ℃时测得放(吸)热为0.65 J/g,80 ℃ 时测得放(吸)热为0.91 J/g.利用公式(20)计算的结果是,40 ℃时放(吸)热为0.39 J/g,80 ℃时放(吸)热为0.44 J/g,接近测量值.理论计算值略小于测量值可能是由于样品的处理问题或测量的方法,该文献作者提到其测量的结果比其他文献报道值都要明显偏大.
综上所述,文中导出的热力学公式具有普遍的意义,适用于凝聚相的任何物质,如果不做密度为常数的近似,也适用于气相的任何物质.计算和分析表明,虽然由于实验方法、测量手段以及实验样品等方面的差别,不同的实验室给出的测量结果存在较大的差异,但这些测量值的定性变化与理论公式的预测完全一致,定量的计算也基本相符.
3 结论
文中通过在热力学基本微分方程中引入极化能,建立了考虑电场作用的热力学微分方程,该微分方程能够有效地描述静电场作用下电介质的热效应.文中导出了电介质的热容、温度、熵和热流量等宏观热力学量随电场强度变化的热力学公式.这些热力学公式的定性预测与文献报道的实验资料完全相同,定量计算也基本相符;同时表明,电热效应与电场强度、介电常数随温度的变化率密切相关;介电常数的温度变化率越大,电热效应越明显.因此,巨电热效应材料的研究方向应该是寻找介电常数(或极化强度)温度变化率大的电介质材料.在相变点附近,分子的重新排列导致电偶极矩的巨大变化,因此相变点附近是电热效应明显的区域.
[1] 韩光泽,陈佳佳.电场强化对流传热的热力学机理 [J].华南理工大学学报(自然科学版),2013,41(12):125- 128. HAN Guang-ze, CHEN Jia-jia.Thermodynamic mechanism of convective heat transfer enhanced by electric field[J].Journal of South China University of Technology(Natural Science Edition),2013,41(12):125- 128.
[2] SUCHANECK G,GERLACH G.Materials and device concepts for electrocaloric refrigeration [J].Physica Scripta,2015,90(9):094020.
[3] LU Sheng-guo,ZHANG Qi-ming.Electrocaloric materials for solid-state refrigeration [J].Advanced Materials,2009,21(19):1983- 1987.
[4] NIKOLA Novak,RASA Pirc,ZDRAVKO Kutnjak.Impact of critical point on piezoelectric and electrocaloric response in barium titanate [J].Physical Review B,2013,87(10):104102.
[5] NIKOLA Novak,ZDRAVKO Kutnjak,RASA Pirc.High-resolution electrocaloric and heat capacity measurements in barium titanate [J].A Letters Journal Exploring the Frontiers of Physics,2013,103(4):47001.
[6] KAR-NARAYAN S,MATHUR N D.Direct and indirect electrocaloric measurements using multilayer capacitors [J].Journal of Physics D:Applied Physics,2010,43(3):032002.
[7] HE Yi.Heat capacity,thermal conductivity,and thermal expansion of barium titanate-based ceramics [J].Thermochimica Acta,2004,419(1):135- 141.
[8] BAI Yang,ZHENG Guangping,SHI Sanqiang.Direct mea-surement of giant electrocaloric effect in BaTiO3multilayer thick film structure beyond theoretical prediction [J].Applied Physics Letters,2010,96(19):192902.
[9] BAI Yang,ZHENG Guang-ping,DING Kai,et al.The giant electrocaloric effect and high effective cooling power near room temperature for BaTiO3thick film[J].Journal of Applied Physics,2011,110(9):094103.
[10] 韩光泽,华贲,陈清林,等.能量的普遍化表达式与能态公设 [J].华南理工大学学报(自然科学版),2001,29(7):48- 50. HAN Guang-ze,HUA Ben,CHEN Qing-lin,et al.The general energy expression and the energy state postulate[J].Journal of South China University of Technology(Natural Science Edition),2001,29(7):48- 50.
[11] 韩光泽,华贲,陈清林,等.热力学中的普遍化表达式 [J].中国科学(A辑),2001,31(10):934- 938. HAN Guang-ze,HUA Ben,CHEN Qing-lin,et al.Genera-lized expression of exergy in the thermodynamics [J].Science in China(Series A),2001,30(10):934- 938.
[12] HAN Guang-ze,HUA Ben.Energy postulate and gene-ralized expressions of energy and exergy [C]∥RIVERO R.Proceedings of ECOS 2004.Mexico:Guanajuato Press,2004:753- 760.[13] HAN Guang-ze,WANG Hui-juan.Generalized expression of chemical potential with influence of external fields and its applications:effect of charged particles on droplet condensation [J].Fluid Phase Equilibria,2013,338:269- 273.
[14] 韩光泽,朱小华.介质中的电磁能量密度及其损耗 [J].郑州大学学报(理学版),2012,44(3):81- 86. HAN Guang-ze,ZHU Xiao-hua.Electromagnetic energy density and its loss in medium [J].Journal of Zhengzhou University(Natural Science Edition),2012,44(3):81- 86.
[15] SCOTT J F.Applications of modern ferroelectrics [J].Science,2007,315(5814):954- 959.
Thermodynamic Mechanism of Electrocaloric Effect of Dielectrics in Electrostatic Field
HAN Guang-ze XING Qian
(Department of Physics, South China University of Technology, Guangzhou 510640, Guangdong, China)
The promising solid-state refrigerator based on the electrocaloric effect plays an important role in the cooling of microelectronic devices. In this paper, a fundamental thermodynamic differential equation considering the polar energy was proposed, and the thermodynamic expressions of heat capacity, temperature, entropy and heat flux in electrostatic field were derived. Then, a verification of the expressions was conducted by using the experimental data of barium titanate, and a good accordance was found. It is concluded that the electrocaloric effect owes itself to the variation of electric dipole moment with temperature and becomes obvious with the increase of temperature sensitivity of permittivity. Thus, the research on giant electrocaloric effect in the future should focus on the drastic change region of permittivity with temperature.
dielectric;electrocaloric effect; thermodynamics; electrostatic field; barium titanate
2016- 06- 16
国家自然科学基金资助项目(51576068) Foundation item: Supported by the National Natural Science Foundation of China(51576068)
韩光泽(1964-),男,博士,教授,主要从事工程热物理研究.E-mail:phgzhan@scut.edu.cn
1000- 565X(2017)06- 0020- 05
O 551;TM 21
10.3969/j.issn.1000-565X.2017.06.004
