立式柱形油品储罐充装中静电电势的动态分布*

王良旺 陈国华

(华南理工大学 安全科学与工程研究所， 广东 广州 510640)

立式柱形油品储罐充装中静电电势的动态分布*

王良旺 陈国华

(华南理工大学 安全科学与工程研究所， 广东 广州 510640)

考虑储罐充装过程中储罐内空间电荷密度随填充时间的变化特性，建立了充装过程中立式柱形储罐内静电电势的动态分布计算模型.对比模型计算结果与文献中的实验测量数据，验证了模型的有效性.将该模型用于分析无输入管道、采用中间鹤管输入、采用底部管道输入3种情况下储罐内空间电势的动态分布规律，发现：3种情况下储罐内的空间最大电势、液面最大电势均随油品填充率先增加后降低；底部输入管道对储罐内静电电势分布的影响较小，中间输入鹤管可以显著降低储罐内的静电电势；采用中间鹤管输入时，保持油品流量恒定，空间电势最大值随鹤管直径增大而减小，流速恒定时空间电势最大值则随鹤管直径增大而增大.研究结果能够为储罐充装过程中输送条件、输送参数的选取提供指导，以降低充装过程中的静电风险.

油品储罐；空间电荷密度；静电电势；动态分布；模型

储罐是石油产品储运的重要设备，储罐注油过程中，油品中的静电电荷随着油品流入储罐，并在储罐内不断积聚，罐内静电电势可达几万甚至几十万伏[1- 2]，极易引发火灾爆炸事故，甚至引发多米诺效应[3- 4].储罐事故中约5%是由静电引起的[5]，因此，研究储罐充装过程中的静电电势分布规律，指导静电危害防控，对于减少静电火灾爆炸事故具有重要意义.

储罐内液相空间、气相空间静电电势分布分别满足Poisson方程和Laplace方程，董巨辉等[6]利用贝塞尔函数、Williams等[7]利用格林公式、Micu等[8]利用分离变量法、王福众[9]利用有限差分法建立了储罐内静电电势的数值计算模型，但在模型计算与分析时均假设储罐内静电电荷密度不随填充时间发生变化.实际充装过程中，油品中静电电荷随油品流入储罐后，通过罐壁、罐底以及其他接地装置逸散，使得储罐内静电电荷密度随填充时间不断变化[1- 2,10- 12].Matsubara等[1]、Udoetok等[13]通过分析储罐内静电电荷的产生、逸散、积聚规律，推导出了储罐内静电电荷密度随填充时间变化的关系式，但并未见到变电荷密度时储罐内静电电势规律的相关理论研究.

输入管道既影响流入储罐内液体携带的电荷量[14- 16]，又通过输送方式(采用底部管道输入、采用中间鹤管输入)影响储罐内静电电势分布[17]，但储罐内静电电势计算模型建立时输入管道的影响通常被忽略[6- 9].王菊芬等[17]将鹤管等效为与储罐同轴的圆柱体，分析了填充率为50%时鹤管直径对储罐内静电电势轴向分布的影响，但输入管道对整个充装过程罐内静电电势的影响还有待进一步研究.

文中充分考虑储罐内静电电势随填充时间变化的特性以及输入管道对储罐内静电电势的影响，建立了充装过程中储罐内静电电势的动态分布计算模型，提出了无输入管道、采用底部管道输入、采用中间鹤管输入3种情况下模型求解的边界条件.应用该模型可以分析充装过程中储罐内静电电势的动态变化规律，以及管道输送方式、管径、液体性质等对储罐内静电电势的影响，为降低储罐内静电电势、提升油品充装过程安全性提供理论依据.

1 储罐内静电电势动态分布模型构建

应用较多的油品储罐是圆柱形立式储罐，如图1(a)所示，半径为R1、高为H(H=H1+H2)的圆柱形立式储罐内液体高度为H1，气相空间高度为H2，以储罐底部圆心O为坐标原点，建立柱坐标系(r,θ,z).文中在建模与计算的过程中忽略了对储罐内静电电势影响较小的附件(如液位计、旋梯等).假设充装过程中储罐内液相空间静电电荷均匀分布，且储罐内气相空间无静电电荷[6,8,17]，则储罐内气相空间电势、液相空间电势分别满足Laplace方程和Poisson方程：

(1)

式中:φg是气相空间电势，V；φl是液相空间电势，V；ρ(t)是空间电荷密度，C/m3；ε=ε0εr，ε是液体介电常数，ε0=8.854×10-12F/m，是真空介电常数，εr是液体的相对介电常数.

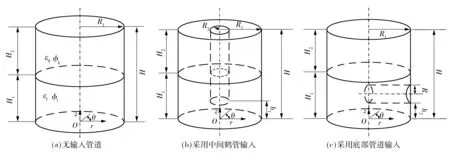
图1 储罐几何模型示意图Fig.1 Schematic diagram of geometrical model for tanks

1.1 边界条件

在进行储罐充装时，可以选择从储罐顶部通过中心鹤管进行(见图1(b))，鹤管与储罐同轴，鹤管半径为R2，鹤管出口端离储罐底部距离为h1.也可以选择从储罐底部通过管道输入(见图1(c))，图中管道的半径为R2，管道长度为R1，管道下端离储罐底部的距离为h2.

(1)无输入管道时(见图1(a))

大型储罐在运行的过程中始终保持良好的接地状态，故储罐壁和储罐底部、顶部的电势均为零，即

(2)

由于电势和电势梯度的连续性，在气液界面处气相空间、液相空间电势值与电势梯度值分别相等，即z=H1时，有

(3)

(2)输入管道位于储罐中心位置时(见图1(b))

当液体从储罐顶部中心位置通过鹤管输入时，鹤管的接地使得鹤管上的电势为零.此时边界条件为

r=R2,h1≤z≤H→φ=0

(4)

(3)输入管道位于储罐底部时(见图1(c))

当液体经过储罐底部的管道输入时，接地管道上的电势为零，此时有

φ(r,θ,z)=0

(5)

其中，

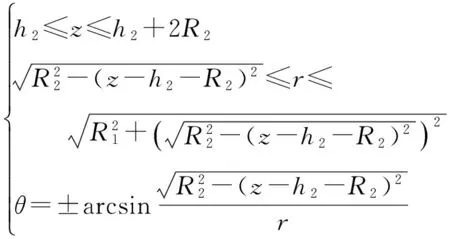
1.2 空间电荷密度

Matsubara等[1]通过分析储罐内静电电荷的产生、逸散、积聚规律，建立了储罐内静电电荷守恒微分方程，求解方程得出填充时间t后储罐内的空间电荷密度为

(6)

(7)

式中：V0为t=0s时刻储罐内存在的液体体积，m3；v为液体在管道中的流动速度，m/s.

当管道足够长时，液体到达出口之前，液体与管壁接触处双电层已经完全形成，Schon通过大量的管道内液体流动起电实验，总结出通过管道直径、液体流速计算静电双电层完全形成的管道内液体流动静电电流的经验公式[18]：

Iin=β(vd)2

(8)

式中：β为比例常数(C·s/m4)；d为管道的直径(m)，文中d=2R2.

将式(7)、(8)代入式(6)，得

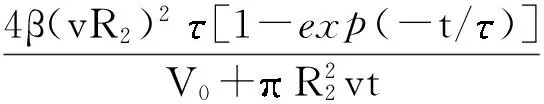
(9)

式(9)即为考虑管道直径、管道内液体流速、液体的逸散时间时，储罐内空间电荷密度随填充时间变化的关系式.将式(9)代入式(1)，并应用边界条件式(2)-(5)，得到不考虑输入管道、采用中间鹤管输入、采用底部管道输入3种情况下罐内静电电势的动态分布计算模型.

2 模型验证与分析

2.1 模型的有效性验证

针对储罐充装过程中储罐内静电电势随填充时间的变化规律，对比文中计算模型的计算结果与Matsubara 等[1]的实验数据，以验证模型的有效性.

Matsubara 等[1]的实验中使用的储罐高度为4.6 m，储罐直径为5.8 m，通过管道输送的油品为煤油，流量为0.9 m3/min，油品电导率为0.1～0.2 pS/m，对比计算时取电导率为0.17 pS/m，相对介电常数为2.空罐注油过程开始阶段罐内油品的飞溅、碰撞以及不均匀分布等不便于实验测量，所以Matsubara 等[1]在开始实验测量时，储罐内已经填充了25%体积的不带电油品.实验中储罐为底部管道注油，因此选用图1(c)的几何模型及式(1)-(3)、(5)进行计算，得出储罐充装过程中液面最大电势随填充时间的变化规律，模型计算结果与Matsubara 等[1]的实验结果对比如图2所示.从图中可以看出，模拟结果能较好地匹配实验结果，相对误差小于7.8%.

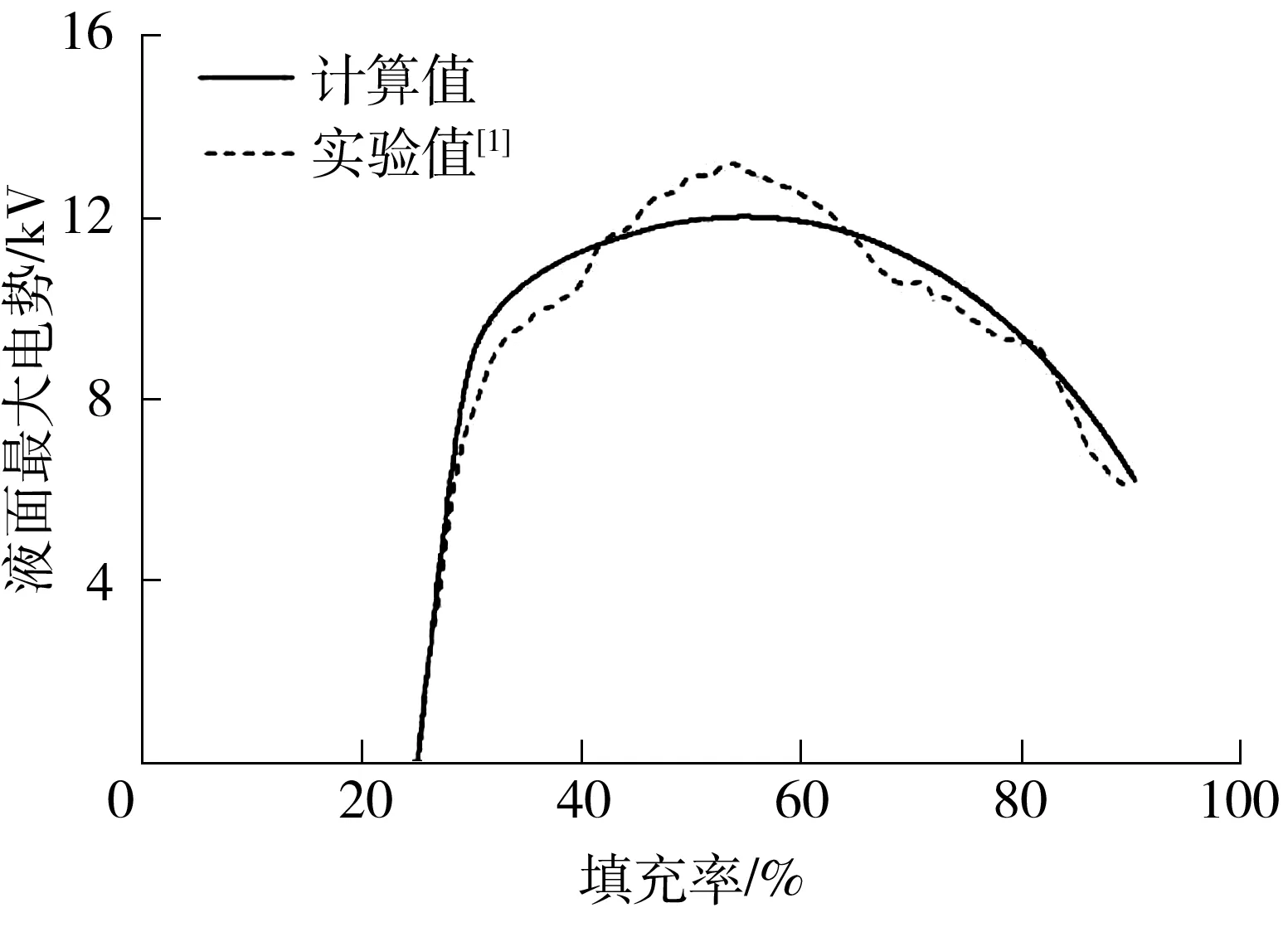
图2 液面最大电势的模拟计算与实验结果对比

Fig.2 Comparison of maximum surface potential between calculation and experimental results

2.2 模型的应用与分析

文中在进行模型分析计算时，液体为煤油，管道、储罐以及煤油相关参数如表1所示(有特别说明的除外)，这些参数均来自实际的工艺过程.

表1 储罐、管道、石油液体参数值Table 1 Parameter values of tank,pipeline and oil

2.2.1 电荷密度恒定时储罐内的电势分布

应用式(1)及边界条件式(2)-(5)，设储罐内空间电荷密度值为恒定值ρ=1.5×10-8C/m3，得出油品填充高度为10 m时，无输入管道、采用中间鹤管输入、采用底部管道输入3种情况下储罐内静电电势的三维分布，如图3所示.3种情况下储罐内空间电势最大值和液面电势最大值随填充率的变化规律如图4所示.图4、5中，下标1表示空间最大电势，2表示液面最大电势；w表示无输入管道，m表示采用中间鹤管输入，b表示采用底部管道输入.

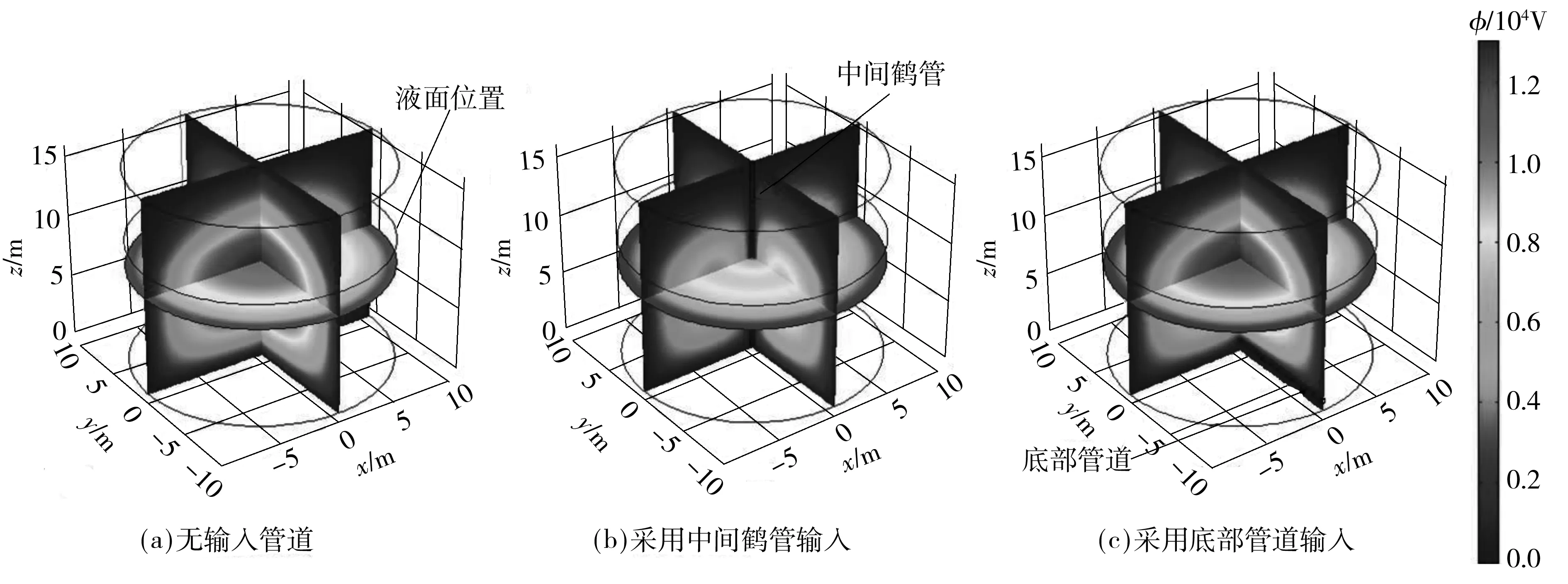
图3 无输入管道、采用鹤管输入、采用底部管道输入情况下储罐内空间电势分布(ρ=1.5×10-8 C/m3，H1=10 m)

Fig.3 Spatial distribution of potential in tanks without pipeline,filling by middle crane tube and filling by bottom pipeline(ρ=1.5×10-8C/m3，H1=10 m)

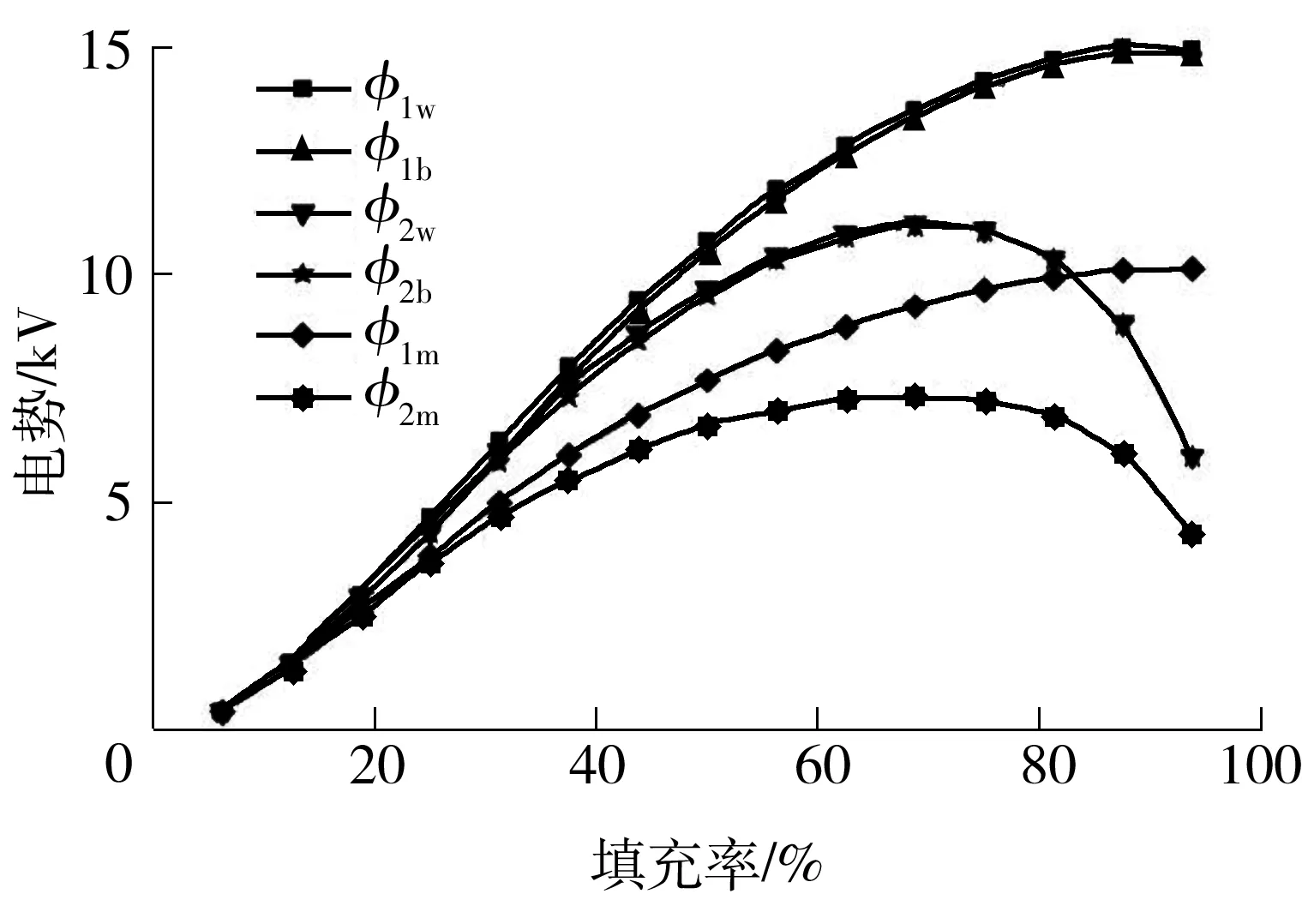
图4 电荷密度恒定时空间最大电势、液面最大电势随填充率的变化

Fig.4 Change of maximum space potential,maximum surface potential with fill fraction at constant charge density

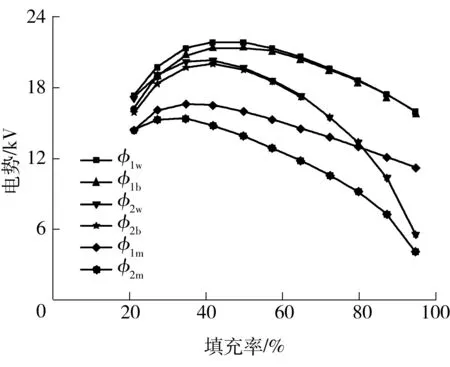
图5 电荷密度变化时空间最大电势、液面最大电势随填充率的变化

Fig.5 Change of maximum space potential,maximum surface potential with fill fraction at various charge density

从图3可以看出，接地的中间鹤管可以显著降低储罐内的静电电势，底部输入管道只对管道周围的静电电势有降低作用，对整个空间的静电电势影响较小.

从图4可以看出，开始填充阶段，3种情况下储罐内空间最大电势、液面最大电势相差较小.随着填充率的增加，无输入管道和采用底部管道输入时，空间最大电势、液面最大电势均相差较小；采用中间鹤管输入时，储罐内空间最大电势、液面最大电势均小于无输入管道和采用底部管道输入情况，并且随着填充率的增加，中间鹤管对电势的降低作用越来越明显.

从图4还可以看出，随着填充率的升高，储罐内空间最大电势逐渐增加，但增加速率逐渐降低，最后趋于水平.液面最大电势随着填充率先增加后降低，在填充率为68%时达到最大值.

2.2.2 电荷密度变化时储罐内的电势分布

将式(9)代入式(1)，得到储罐内电荷密度随填充时间变化时储罐内的空间电势分布方程，应用边界条件式(2)-(5)求解方程，分析储罐内空间电荷密度随填充时间变化时储罐内空间电势的分布规律.充装过程开始时，储罐内初始液体体积为1 000 m3(初始填充率为20%).

(1)输入管道对静电电势的影响

图5为储罐内空间电荷密度随填充时间变化时，储罐内空间最大电势与液面最大电势随填充率的变化图.从图5可以看出，随着填充率的升高，采用中间鹤管输入、底部管道输入或无输入管道3种情况下，储罐内空间最大电势和液面最大电势均先增加后降低.

对比图5中采用底部管道输入时气液界面处最大电势变化曲线与文献[1- 2]中的实验结果，液面电势最大值均为先快速增加后降低，并且在增加填充20%～25%液体后达到最大值.图4以及文献[6,9]中假设储罐内静电电荷不随填充时间变化，在填充率为70%左右达到液面电势最大值.这说明考虑储罐内静电电荷密度随填充时间变化时的计算结果与实验结果更吻合.

图6是填充时间分别为1 000、2 000、3 000、4 000 s时，无输入管道、采用中间鹤管输入、采用底部管道输入3种情况下，储罐内空间电势分布的剖面图.从图6中可以看出：中间输入鹤管使得储罐内空间电势分布呈现由罐壁到中间鹤管先增加后降低的趋势；底部输入管道只影响管道附近的电势分布.无输入管道和采用底部管道输入时，液面最大电势均在储罐轴线上.

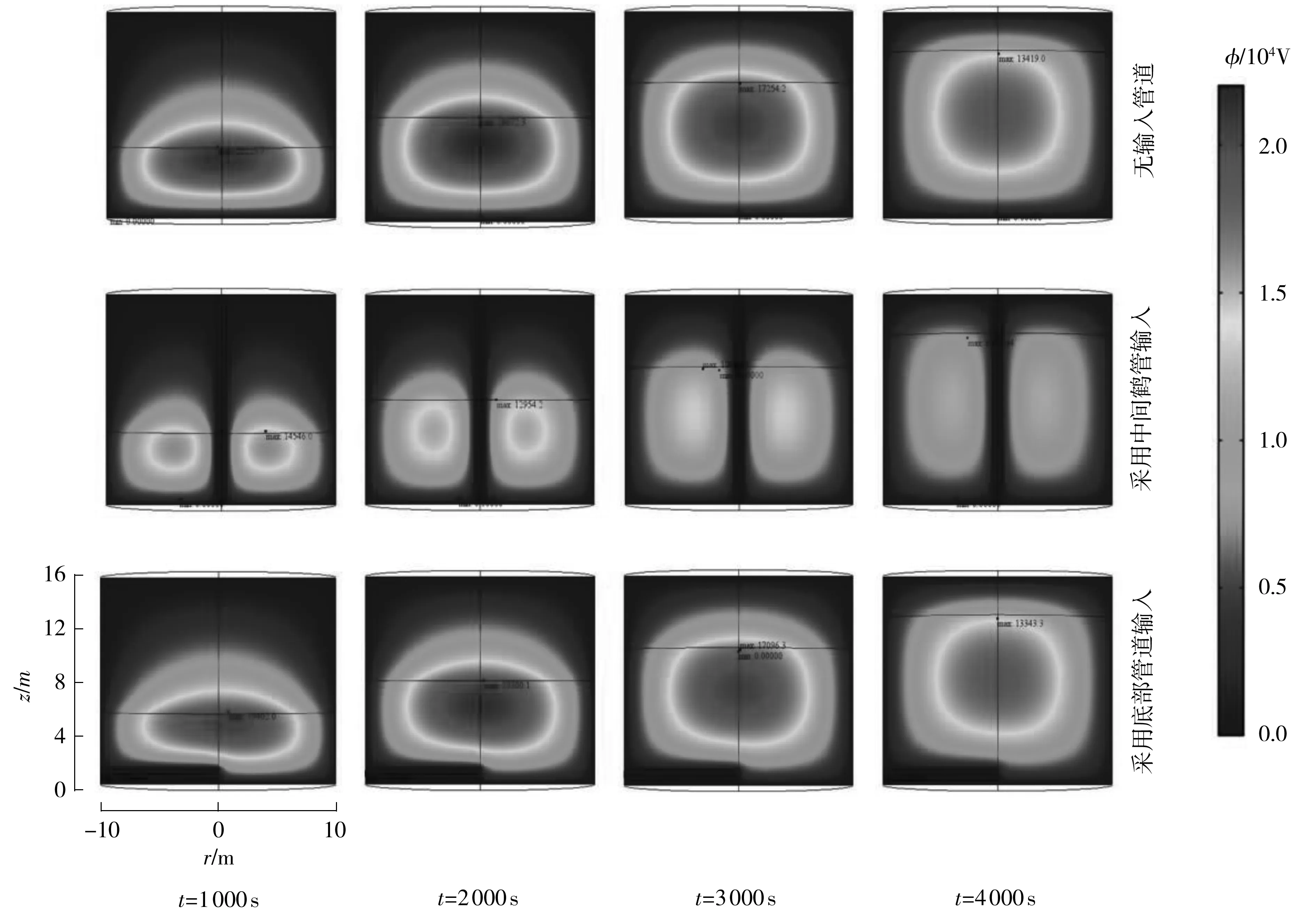
图6 电荷密度变化时无输入管道、采用中间鹤管输入、采用底部管道输入3种情况下储罐内的电势分布剖面图

Fig.6 Cross-section views of potential in tanks without pipeline,with middle crane tube filling and with bottom pipeline filling at various charge density

(2)管道直径对电势的影响

由式(9)可知，管道的直径直接影响储罐的输入电荷密度.由图5可以看出，当采用底部管道输入时，底部输入管道对空间电势的影响可以忽略，即底部输入管道只通过影响储罐的输入电荷密度影响储罐内的空间电势；中间鹤管既影响储罐的输入电流，又通过接地影响储罐内的静电电势分布，因此，文中选择中间鹤管输入方式分析管道直径对储罐内静电电势的影响.

图7是油品流量恒定为0.2 m3/s，鹤管直径分别为0.2、0.3、0.4和0.5 m时，储罐内空间电势最大值随填充率的变化图.从图7可以看出，流量恒定时，充装相同的填充率，鹤管管径越大储罐内的空间最大电势值越小；但随着鹤管管径的增加，空间最大电势的降低幅度逐渐变小.

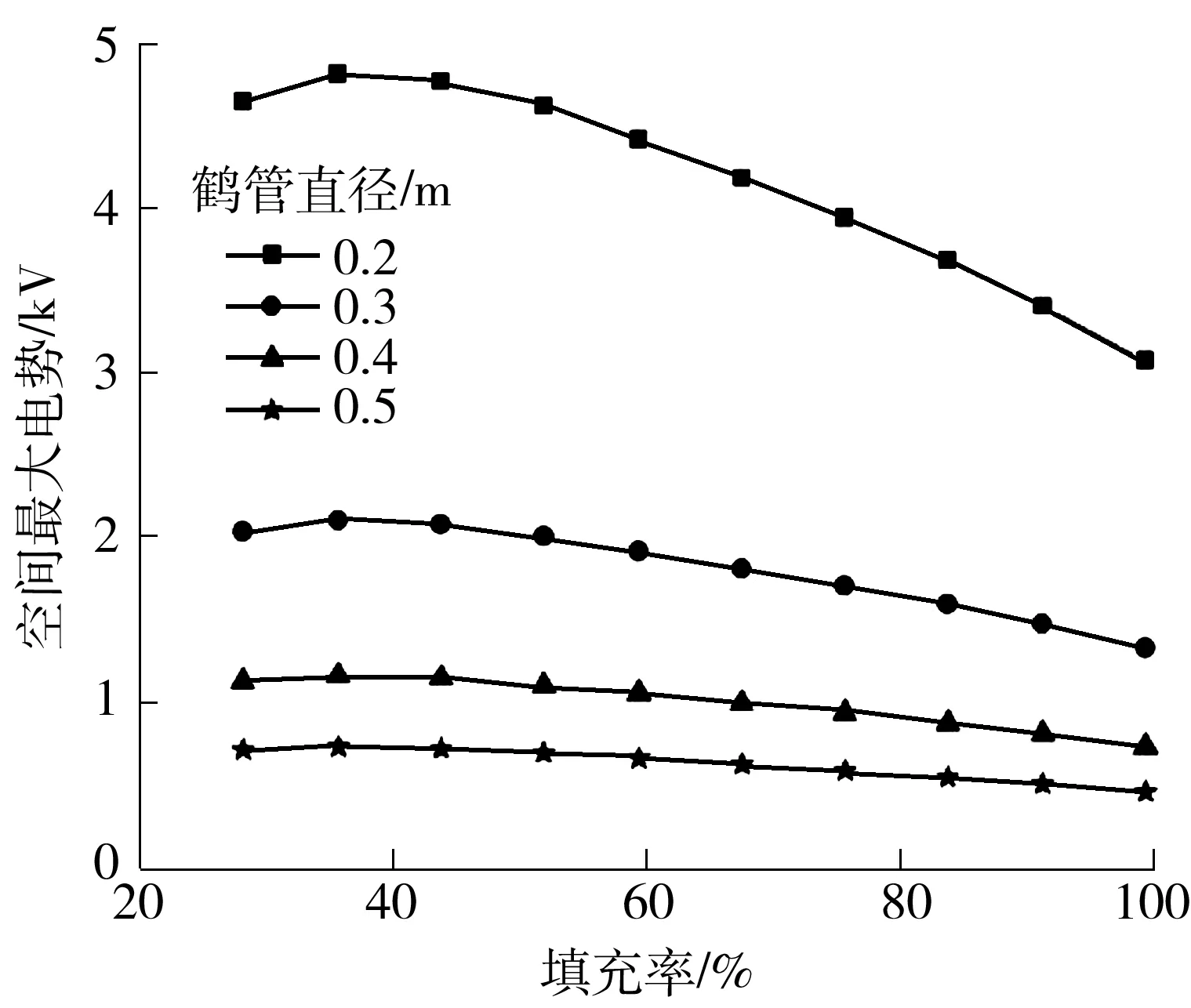
图7 流量恒定为0.2 m3/s时不同管径下空间最大电势随填充率的变化

Fig.7 Maximum space potential variation versus fill fraction for different pipeline diameters at the flow rate of 0.2 m3/s

图8是油品流速恒定为6 m/s，鹤管直径分别为0.2、0.3、0.4和0.5 m时，储罐内空间电势最大值随液体填充率的变化图.从图8可以看出，流速恒定时，充装相同的填充率，鹤管管径越大储罐内的空间最大电势值越大.一方面由式(9)可知，鹤管管径增加使得管道内流动电流增大，从而引起储罐内静电电势的升高，另一方面鹤管管径的增加使得储罐内静电电势降低，由图8可知，前者对电势的增加作用要大于后者.

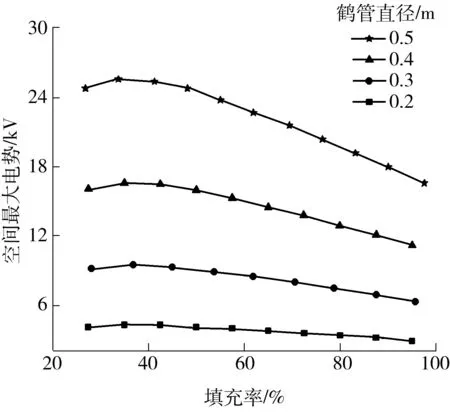
图8 流速恒定为6 m/s时不同管径下空间最大电势随填充率的变化

Fig.8 Maximum space potential variation versus fill fraction for different pipeline diameters at the flow velocity of 6 m/s

3 结论

(1)文中考虑储罐充装过程储罐内静电电荷密度随填充时间变化的特性，建立了储罐内静电电势动态分布计算模型，应用该模型能够较为准确地计算无输入管道、采用中间鹤管输入、采用底部管道输入3种情况下储罐内空间电势的动态分布.

(2)底部输入管道对储罐内空间电势影响较小；中间鹤管改变了储罐内空间电势分布，可以显著降低储罐内空间电势；选择中间鹤管输入是降低储罐充装过程静电风险的有效措施.

(3)考虑储罐内空间电荷密度随填充时间的变化时，储罐内空间电势最大值、液面电势最大值均随油品填充率先快速增加后降低，在增加填充20%～25%储罐容积的油品后达到最大值.

(4)采用中间鹤管输入时，保持油品流量恒定，空间电势最大值随鹤管管径的增大而减小；保持油品流速恒定，空间电势最大值随鹤管管径的增加而增大；为降低储罐内静电电势，相同流量下应选择较大管径，而相同流速时应选择较小管径.

[1] MATSUBARA Y,MATSUSHIMA S,JONES T B.Charge accumulation in an oil tank during loading operations [J].Journal of Electrostatics,1997,40/41(1):191- 197.

[2] SUN K P,LIU Q Z,LI X W.Simulation test on charge density and surface potential in an oil tank during filling operation [J].Journal of Electrostatics,2009,67(2/3):340- 341.

[3] 蒋国辉，张晓明，闫春晖，等.国内外储罐事故案例及储罐标准修改建议 [J].油气储运，2013,32(6):633- 637. JIANG Guo-hui,ZHANG Xiao-ming,YAN Chun-hui.et al.Worldwide tank accidents and tank standards revision advices [J].Oil & Gas Storage and Transportations，2013,32(6):633- 637.

[4] 张虹，谢翔．油库火灾爆炸事故原因分析及控制 [J]．石油化工安全技术，2006，22(4)：21- 25. ZHANG Hong,XIE Xiang.Case analysis and control of fire explosion hazard in oil deport [J].Petrochemical Safety and Environmental Protection Technology,2006，22(4)：21- 25.

[5] CHANG J I,LIN C C.A study of storage tank accidents [J].Journal of Loss Prevention in the Process Industries,2006,19(1):51- 59.

[6] 董巨辉，黄永华.低导电性油品及液氢流体在储罐内的静电电位计算 [J].化工学报，2014，65(S1):409- 414. DONG Ju-hui,HUANG Yong-hua.Calculation of electrostatic potential of low conductivity hydrocarbon products and liquid hydrogen in tanks [J].Journal of Chemical Industry and Engineering,2014，65(S1):409- 414.

[7] WILLIAMS T J,JONES R T.Modelling the electrostatic ignition hazards associated with the cleaning of tanks containing flammable atmospheres [J].Journal of Loss Prevention in the Process Industries,2001,14(2):129- 133.

[8] MICU D D,MICU D.Electric field computation inside a rectangular petrol tank [J].Journal of Electrostatics,2013,71(3):332- 335.

[9] 王福众.大型钢制石油储罐内的静电分布规律研究 [D].青岛：中国石油大学(华东)，2010.

[10] WALMSLEY H L.The calculation of the electrostatic potentials that occur when tanks are filled with charged li-quids [J].Journal of Electrostatics,1991,26(3)：201- 226.

[11] WALMSLEY H L.The electrostatic potentials generated by loading multiple batches of product into a road tanker compartment [J].Journal of Electrostatics,1996,38(3):177- 186.

[12] BRITTON L G.Avoiding static ignition hazards in che-mical operations [M].New York:AIChE,2000.

[13] UDOETOK E S,NGUYEN A N.Grounding resistance for control of static electricity ignition hazards [J].Journal of Electrostatics,2009,67(2/3):247- 250.

[14] GLOR M.Ignition source static electricity：incident investigation [J].Journal of Electrostatics，2009,67(2/3)：242- 246.

[15] GLOR M.Hazards and problems associated with liquids [J].Journal of Electrostatics,2001,51/52(1):359- 365.

[16] HEARN G L.Electrostatic ignition hazards arising from fuel flow in plastic pipelines [J].Journal of Loss Prevention in the Process Industries,2002,15(2):105- 109.

[17] 王菊芬，蒲家宁，孟浩龙.鹤管对储罐内静电场影响分析 [J].天然气与石油，2006,24(6)：5- 8. WANG Ju-fen,PU Jia-ning,MENG Hao-long.Analysis on the electrostatic behavior in a vessel with filling pipe [J].Natural Gas and Oil,2006,24(6)：5- 8.

[18] BRITTON L G,SMITH J A.Static hazards of the VAST [J].Journal of Loss Prevention in the Process Industries,2012,25(2):309- 328.

Dynamic Distribution of Electrostatic Potential in Vertical Cylindrical Oil Tank During Filling

WANG Liang-wang CHEN Guo-hua

(Institute of Safety Science and Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

In this paper, first, by taking into consideration the variation of space charge density with the filling time in oil tanks in the filling process, a dynamic distribution model of electrostatic potential in vertical cylindrical oil tanks is established. Then, the effectiveness of the model is verified by comparing the results obtained by the model with the experimental ones in the literature. Finally, the proposed model is employed to analyze the dynamic distribution laws of electrostatic potential in three kinds of tanks respectively without filling pipeline, with middle crane tube filling and with bottom pipeline filling. The results show that (1) both the maximum spatial potential and the maximum oil-surface potential of the three above-mentioned tanks first increase and then decrease with the oil filling rate; (2) the bottom pipeline slightly affects the electrostatic potential distribution in tanks, while the middle crane tube significantly reduces the potential; and (3) with the diameter increase of the middle crane tube, the maximum spatial potential decreases at constant filling flux but increases at constant filling velocity. This research provides references for the selection of transportation conditions and parameters and helps to reduce the electrostatic risk du-ring the filling of oil into tanks.

oil tank; space charge density; electrostatic potential; dynamic distribution; model

2016- 05- 03

国家自然科学基金资助项目(21576102) Foundation item: Supported by the National Natural Science Foundation of China(21576102)

王良旺(1990-)，男，博士生，主要从事工业安全与风险评估研究.E-mail：wanglw1990@163.com

1000- 565X(2017)06- 0008- 07

TE 88

10.3969/j.issn.1000-565X.2017.06.002