纳米孪晶超硬材料的高压合成∗

徐波 田永君

(燕山大学亚稳材料制备技术与科学国家重点实验室,秦皇岛 066004)(2016年10月10日收到;2016年10月24日收到修改稿)

专题:高压下物质的新结构与新性质研究进展

纳米孪晶超硬材料的高压合成∗

徐波 田永君†

(燕山大学亚稳材料制备技术与科学国家重点实验室,秦皇岛 066004)(2016年10月10日收到;2016年10月24日收到修改稿)

超硬材料研究有两个重要难题一直备受关注:一是建立晶体宏观性能硬度与微观电子结构参数的定量关联,指导新型超硬晶体的设计;二是发现改进超硬材料综合性能(硬度、韧性和稳定性)的基本原理和技术途径,合成出综合性能更加优异的高性能超硬材料.首先从同时联系晶体硬度和电子结构的化学键出发,提出了共价晶体的压痕硬度为晶体中化学键对压头压入过程的综合阻抗的基本假设,建立了共价晶体硬度的微观模型并推广至多晶共价材料.在多晶硬度模型指导下,在高温高压条件下成功地合成出了纳米孪晶结构的立方氮化硼和金刚石块材,实现了硬度、韧性及热稳定性这三大工具材料性能指标的同时提高.另外,澄清了关于压痕硬度测量的长期争论.本文的研究为研发高性能超硬材料打开了一条新的技术途径,有望带来机械加工业和高压科学领域的新变革.

超硬材料,霍尔-佩奇效应,量子限域效应,纳米孪晶

1 引 言

维氏硬度(HV)超过40 GPa的材料被称为超硬材料,其中HV超过80GPa的材料又被称为极硬材料[1].这类材料都是共价固体,具有优越的硬度、不可压缩性和耐磨性,因而成为不可或缺的工具材料并被广泛应用于车削、切割、研磨、钻探等一系列现代加工业操作中.金刚石和立方氮化硼(cBN)是最重要的两种超硬材料,在20世纪中叶相继实现了人工合成[2,3].采用这两种超硬材料制造的各类超硬刀具、磨具、钻头等已在工业上得到了广泛应用;金刚石对顶砧作为超高压发生装置也在地球科学、高压物理和材料科学等研究领域中发挥着不可替代的作用.

然而金刚石和cBN都存在着各自的不足.金刚石容易与铁基金属反应且热稳定性较差.当温度超过800◦C时,金刚石在空气中将发生石墨化从而丧失超硬特性[4].cBN热稳定性较好、适合加工铁基材料,但硬度和断裂韧性明显偏低,还不足金刚石的一半.此外,这两种超硬材料还存在着一个共同的弱点:由于化学键的强共价性,金刚石和cBN粉体的烧结性极差.当使用金刚石或cBN粉体制备烧结块材时通常要使用金属钴做结合剂,获得的金刚石聚晶(PCD)或cBN聚晶(PCBN)的力学性能都难以超过单晶本身.随着经济和高技术的蓬勃发展,全球对超硬材料的需求持续增长,预计到2020年,超硬材料全球市场将达到230亿美元[5].与此同时,更加严格的环境立法也推动了超硬材料的新发展,例如可用于无冷却液、高速干式切削加工的超硬材料.因此,合成出综合性能(硬度、断裂韧性、热稳定性等)更加优异的新型超硬材料就成为科学界和产业界共同追求的目标.此外,天然金刚石长期以来一直作为自然界中最硬的材料而被人们所熟知.天然金刚石单晶的硬度呈现明显的各向异性.根据晶体学取向的不同,其硬度分布在60—120 GPa之间[6].自人工合成金刚石之日起,合成出比天然金刚石更硬的人工材料就一直是人类的梦想[7].人们在实现这一梦想的过程中经历过失望和疑惑[8,9],但最终还是获得了成功[10].

在过去的十几年间,人们在超硬材料研究领域取得了突破性的进展.理论上,建立了共价晶体的硬度微观模型[11−13].这些模型将共价晶体的宏观性能——硬度与微观可计算参量定量地联系起来,可定量预测出假想晶体结构的理论硬度,从而为新型超硬晶体的设计提供了行之有效的方法和工具.实验上,通过细化材料的晶粒尺寸,金刚石和cBN的硬度得到显著提高[14−17];在纳米晶内部再形成平均厚度为几个纳米的孪晶亚结构,可以同时提高金刚石和cBN的硬度、热稳定性和断裂韧性[10,18].业已证明,纳米结构化是制备高性能多晶超硬材料的有效途径.

本文首先讨论共价晶体硬度的微观模型,并将这一模型推广到多晶共价材料;然后介绍纳米孪晶极硬材料的设计原理、实验合成和硬度测量原理方面的研究工作;最后展望了纳米孪晶极硬材料的可能应用.需要强调的是,本文侧重于总结我们课题组在超硬材料研究中的主要进展.关于超硬材料研究更全面的概述,已有很多优秀的综述文章可供感兴趣的读者参考[19−23].

2 共价晶体和多晶材料的硬度模型

硬度是衡量材料对永久塑性变形综合阻抗的一个宏观性能参量.早期的宏观硬度模型试图在材料硬度与弹性性质之间建立起关联,例如体弹模量模型、剪切模量模型等[24−26].这些宏观模型虽然可以为硬度预测提供初步的定性估计,但所给出的硬度与体弹模量或剪切模量的直接关联缺乏切实的物理基础:弹性模量仅反映了材料对弹性变形的响应,而硬度却是材料对塑性变形的响应.针对这一难题,我们课题组于2003年提出了一个重要的、启发性的假设,将共价晶体宏观上的塑性变形与微观上化学键断裂所伴随的电子跃迁联系起来,从而建立了共价晶体硬度的微观模型[11].

图1 (a)硬度测量过程中压头下面化学键的变化;(b)伴随化学键断裂的电子跃迁;(c)纯共价键与极性共价键中价电子(VE)的分布[21]Fig.1.(a)Response of chemical bonds under an indenter during a hardness measurement;(b)electron excitation accompanying chemical bond breaking;(c)the distribution of valence electrons(VE)in pure and polar covalent bonds[21].

2.1 共价单晶硬度的微观模型

单晶的塑性变形起源于晶体内的位错滑移,而位错滑移又与化学键的断裂相联系.具体到压痕硬度测量过程,如图1(a)所示:压头压入一块共价单晶时,压头尖端附近的共价键将发生断裂,位错开动并进一步导致晶体发生塑性变形.基于这一简单的物理图像,我们提出了一个基本假设:共价单晶的硬度在微观上可诠释为单位面积上每个化学键对压头的阻抗之和[11].也就是说化学键密度越高、键越强,晶体硬度就越高.对于共价晶体,如图1(b)所示,化学键的断裂意味着两个成键电子从价带跃迁到导带,单个化学键所产生的阻抗就可以用材料的平均共价带隙Eg来评估.这样,纯共价单晶的维氏硬度(单位GPa)就可以表示为[11]

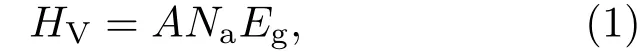
这里,比例系数A对于只含s和p价电子的晶体取值为14;Na=(Ne/2)2/3是单位面积内的共价键数目,Ne为价电子密度(单位1/Å3);按照Phillips的介电理论[27],Eg=39.74d−2.5,d为化学键键长(单位Å).对于极性共价单晶,如图1(c)所示,价电子的分布偏向阴离子,化学键呈部分离子性,这就在一定程度上降低了化学键的强度.考虑到化学键离子性带来的弱化效应,需在(1)式中引入一个修正因子e−αfi.这里fi是极性共价键的Phillips离子性[27],α为拟合常数.这样,极性共价单晶的维氏硬度就可以表示为[11]

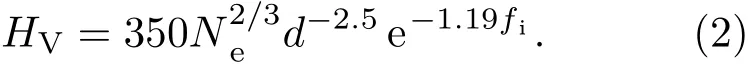
此外,某些极性共价晶体的化学键还涉及到d轨道电子并具有少量的金属性,比如过渡金属的碳化物、氮化物、硼化物等[28,29].一方面,由于更强的方向性及更高的轨道强度,s-p-d杂化的化学键键强要高于s-p杂化的化学键,这对于提高材料硬度是有利的;另一方面,金属性的存在严重影响了晶体的硬度,这一点与化学键离子性对晶体硬度的影响相类似[30].考虑到这两方面因素的共同作用,这类晶体硬度可以表示为.这里fm是一个衡量化学键金属性的因子,具体的定义及计算方法读者可以参考文献[30].

这一共价单晶的硬度模型可以很容易地推广至晶体内部包含两个以上不同类型共价键的复杂晶体.这时的单晶硬度可以看作内部不同类型共价键硬度的几何平均[11]:

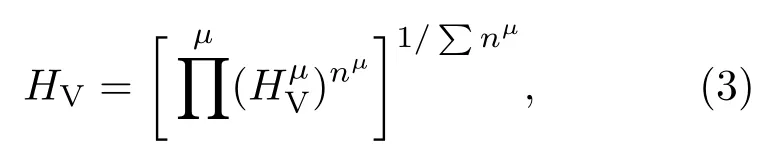
这里nµ是单胞中第µ种化学键的数目,为仅含第µ种化学键的晶体的硬度.第µ种化学键若包含d价电子则A0取1051,否则取350.

尽管硬度作为一个工程上的性能参量无法基于量子力学进行直接估算[31],但上述半经验的硬度模型成功地在硬度与微观可计算参量之间建立起联系.该模型显示,共价晶体的硬度是一个带隙相关的性质,取决于晶体的三个微观参量:价电子密度、键长和键的离子性(及金属性).根据这一模型,人们可以准确地预测出所设计亚稳结构的硬度,预测精度在10%以内[22].在我们的硬度微观诠释启发下,人们相继提出了更多的硬度微观模型[12,13,32].这些模型结合先进的晶体结构搜索方法[33−38],为理论设计新颖的超硬结构晶体提供了强有力的工具.

2.2 多晶共价材料的硬化效应

寻找比天然金刚石更硬的人工材料可能有两条途径:一是在新型超硬结构晶体中去寻找,二是把现有超硬材料的硬度成倍提高.最近的一项理论工作详细研究了碳的众多可能的同素异构体[39],并结合硬度的微观模型[12]预测了这些结构的硬度,发现金刚石在所有理论预测的碳同素异构体中是最硬的.十多年来类似的探索发现找到比金刚石更硬的单晶材料几乎是不可能的.于是人们开始把目光转向多晶共价材料,因为多晶材料的硬度随显微组织特征尺寸减小而增大,这就是著名的霍尔-佩奇效应[40,41].但是,根据多晶金属材料硬化的传统图像,当显微组织特征尺寸小于约10 nm时,晶界滑移等协同效应就开始起主导作用,材料开始软化[42].换句话说,多晶金属材料存在约10 nm这个硬化尺寸下限.对于多晶共价材料,能不能突破这个硬化尺寸下限?如能突破,共价材料硬度提高的幅度到底能有多大？下面我们就来分析这些问题.

前面讨论的共价单晶硬度的微观模型可以用来预测材料的本征硬度.我们知道,硬度表征一个材料抵抗塑性变形的能力,与材料的组织结构有着密切的联系.也就是说,多晶共价材料的硬度不仅要考虑材料的本征硬度,还需要计入与材料组织结构相关的、额外的非本征硬化效应.纳米结构化的多晶共价材料中有两种主要的硬化效应,分别是霍尔-佩奇效应[40,41]和量子限域效应[43].多晶材料的塑性变形主要通过单个晶粒内的位错滑移来实现.晶界能够有效抑制位错的产生及移动,从而增加材料的变形难度.晶界对硬度的贡献通常按照霍尔-佩奇关系表示为HHP=KHPD−1/2,这里D是平均晶粒尺寸,KHP是一个材料相关的常数.同时,共价单晶硬度的微观模型显示硬度是一个带隙相关的性质.根据Kubo理论[44],纳米晶的带隙随着晶粒体积的减小而增大.实验上也已证实,金刚石、硅等多晶共价材料的带隙随着晶粒尺寸的降低而增大[45,46].这样,随着多晶共价材料内晶粒尺寸减小到纳米量级,就会因为平均带隙增大而产生一个额外的硬化效应——量子限域效应[43].源于量子限域效应的硬度增强可以表示为Hqc=KqcD−1,这里D是平均晶粒尺寸,Kqc是一个材料相关的常数.由于尺寸效应引起的硬化效果已经在直径为20—50 nm的硅纳米球中得到了证实,这些硅纳米球的硬度与大块硅单晶相比提高了2—4倍[47].将霍尔-佩奇效应和量子限域效应综合起来,烧结致密的多晶共价材料的硬度可以表示为

其中H0是完整单晶的本征硬度.这样我们就构建了多晶共价材料的硬度模型.该模型表明,多晶共价材料的硬度是一个既位错相关又带隙相关的性质.对于共价材料,即便在纳米尺度晶界滑移导致霍尔-佩奇效应失效,量子限域效应的存在仍可以保证多晶共价材料的持续硬化,从而突破约10 nm这一硬化尺寸下限.显微组织的特征尺寸越小,多晶共价材料的硬度就越高.

3 纳米结构化超硬材料

前面的分析表明,纳米结构化是提高共价材料硬度的有效途径,这在实验合成的纳米晶(nanograined)金刚石和cBN块材中首先得到证实.2003年,Irifune等[15]利用高温高压条件下石墨的马氏体相变,合成了极硬的纳米晶金刚石块材,块材中晶粒尺寸可控制在10—20 nm,努氏硬度(HK)达到110—140 GPa.在高温高压的条件下,人们又相继合成出聚合金刚石纳米棒[48]、纳米晶cBN[17,49]和聚合氮化硼纳米复合材料[14].这些材料除了具有很高的硬度外,其刚度[50]、耐磨性和断裂韧性[16,51]、热稳定性等[14]其他性质也得到了提高.此外,由于纳米晶超硬块材内部的晶粒取向是随机的,所以材料的性能呈现各向同性的特征,不像单晶那样呈现出明显的硬度各向异性及解理特性.这些优点无论对科学应用还是工业应用都是十分有利的[52,53].

值得注意的是,这些纳米晶超硬块材的晶粒尺寸一般都在10 nm以上.按照(4)式的预测,如果可以进一步降低晶粒尺寸,材料会变得更硬.然而对于普通的纳米晶材料,因大角度晶界的过剩能较高,在合成温度下纳米晶粒的生长驱动力就很大,想要获得更小的晶粒尺寸是很难实现的.降低合成温度的确可以减小纳米晶粒的尺寸[14,54],但是这样制备出的样品,硬度不但没有提高,反而变得更低.所观察到的这种软化现象并不是来自于反霍尔-佩奇效应,而是源于低合成温度所导致的低晶界强度,从而容易发生沿晶断裂[54].到目前为止,在保证晶界烧结良好的同时保持更小的晶粒尺寸仍然是一个技术上的挑战.

在纳米尺度,纳米晶和纳米孪晶是两种典型的显微组织结构.共格的孪晶界具有与大角度晶界相同的硬化效应[55,56].更重要的是,孪晶界的过剩能比大角度晶界的过剩能低一个数量级以上[55],孪晶的生长驱动力就变得很小,这为获得超细的纳米结构提供了机会和可能性.如果在超硬材料中能够形成纳米孪晶结构就可能获得超细的显微组织结构,因此超硬材料组织的孪晶化是获得比金刚石更硬的人工材料的现实途径.采用高温高压条件下的马氏体相变来形成超细纳米孪晶结构必须满足以下两个条件:相变成核时相邻晶核存在大的取向差和高的相变成核率.大取向差确保相邻晶核不发生合并长大而只能形成孪晶,而高成核率能够保证孪晶细小.实验上,可以通过选择合适结构的前驱体来满足这些条件,例如我们使用的具有高密度层错的洋葱结构前驱体[10,18].此外,洋葱结构前驱体能量较高,相变驱动力大,这一特点有助于降低合成条件(例如合成温度).这一点也在我们的实验中得到了证实.

使用直径30—150 nm的洋葱结构氮化硼纳米颗粒为前驱体,我们在高温高压条件下合成了透明的全纳米孪晶结构cBN块材[18].图2给出了洋葱氮化硼前驱体及纳米孪晶cBN的典型显微结构.对样品的透射电镜分析表明,cBN纳米晶粒内部形成了大量的片状孪晶,平均孪晶厚度仅为3.8 nm.与cBN单晶相比,该材料的硬度及断裂韧性得到了极大的提高:维氏硬度可达100 GPa,是单晶的2—3倍,断裂韧性超过了12 MPa.m0.5,是单晶的4倍,从根本上克服了传统cBN单晶材料的缺点.此外,纳米孪晶cBN在空气中的抗氧化温度也比单晶提高了191◦C.

按照相同的原理,以直径20—50 nm碳洋葱纳米颗粒为相变前驱体,我们在高温高压下又成功地合成了透明的纳米孪晶金刚石块材[10].在金刚石纳米晶粒内部,同样观察到高密度的片状{111}纳米孪晶,平均孪晶厚度为5 nm.该样品展现了更加优异的力学性能:我们测得的维氏和努氏硬度均约为200 GPa,是天然金刚石单晶硬度值的两倍.毫无疑问,这种人工材料比天然金刚石更硬,其断裂韧性达到10—15 MPa.m0.5,与商用硬质合金相当.此外,纳米孪晶金刚石的抗氧化温度达到了1056◦C,比天然金刚石高出200◦C以上.

为了验证合成样品的可重复性及硬度测量的准确性,我们按照图3所示样品的合成条件(20 GPa,2000◦C),另外合成了四个纳米孪晶金刚石样品,提供给吉林大学超硬材料国家重点实验室进行硬度测量.采用相同的测量条件(4.9 N的载荷下保压10 s),四个样品的HV分别为191,196,196和200 GPa,与我们的测量结果一致,说明纳米孪晶金刚石样品的制备具有非常好的可重复性(表1).

图2 (a)洋葱氮化硼纳米颗粒的透射电镜照片,插图显示的是红框区域的高分辨透射电镜照片,弯曲的氮化硼原子层、晶格褶皱及高密度层错清晰可见;(b)cBN纳米晶粒的透射电镜明场像,插图显示了一块直径2 mm的纳米孪晶cBN块材;(c)沿(b)中所示纳米晶粒的[101]带轴观察的高分辨透射电镜照片及相应的选区电子衍射图,纳米晶粒内含有大量厚薄不一的片状纳米孪晶,孪晶面为{111},跨过孪晶面的晶格条纹角度为70.53◦,红色三角标注了两个肖特基位错[18]Fig.2.(a)Transmission electron microscopy(TEM)image of onion BN nanoparticles,and the inset is high resolution TEM(HRTEM)image corresponding tothe position marked with the red box emphasizing featu res of cu rved atomic layers,lattice puckering,and stacking fau lts;(b)bright field TEMimage of a cBN nanograin,and the inset shows an nt-cBN bu lk sample with a d iameter of 2 mm;(c)HRTEMimage and corresponding selected area electron d iff raction pattern(SAED,inset)along the[101]zone axis of the nanograin shown in(b),lamellar nanotwins with various thicknesses(λ)are present in the nanograin,the twinning plane is of the{111}typewith lattice fringe angles of 70.53◦across the twin plane,the red triangles mark twoShock ley dislocations[18].

图3 (a)洋葱碳纳米颗粒的高分辨透射电镜照片;(b)纳米孪晶显微结构的透射电镜照片,插图显示了一块尺寸1 mm的透明样品照片;(c)沿金刚石[101]带轴观察的、与(b)中红框区域对应的交错纳米孪晶的高分辨透射电镜照片,片状孪晶、堆垛层错清晰可见,孪晶界用红色箭头标记,普通晶界终止于联锁的孪晶区域,插图显示的是对应(b)中心区域的选区电子衍射图,带有四重特征的衍射斑来源于观察区域包含的四种不同取向孪晶[10]Fig.3.(a)HRTEMimage of onion carbon nanoparticles;(b)TEMimage of nanotwinned microstructu re,the inset shows a photograph of the transparent sample(1 mmin diameter);(c)HRTEMimage of intersecting nanotwins(marked with the red box in b),viewed along the[101]zone axis of d iamond,lamellar{111}nanotwins,stacking fau lts are present,twin boundaries aremarked with red arrows,grain boundaries(GB)are interrupted by interlocked twins,the inset shows SAED pattern correspond ing tothe central area of(b),the four-fold-like pattern is fromthe twin domainswith four diff erent orientations[10].

表1 五个纳米孪晶金刚石的维氏硬度(单位GPa)测量结果,其中376号样品的硬度在燕山大学测量,其余四个样品的硬度在吉林大学测量Tab le 1.V ickers hardness(in the unit of GPa)of 5 nanotwinned d iamond samples,the hardness of sample 376 wasmeasu red in Yanshan University,all the others were measu red in Jilin University.

纳米孪晶金刚石和cBN的实验结果表明,纳米孪晶化可以同时提高超硬材料的硬度、韧性和热稳定性三大关键性能指标.随着显微组织特征尺寸(孪晶厚度)的进一步降低,共价材料可以发生持续硬化,这也验证了我们所提出的多晶共价材料的硬度模型.纳米孪晶组织还解决了超硬材料硬度与韧性的倒置问题,在硬化的同时提高了韧性.与大角晶界不同,位错可以沿着密集分布的共格孪晶界滑移,有效地降低了应力集中,抑制了裂纹扩展,从而提高了材料韧性[57,58].根据碳和氮化硼温度-压力平衡相图[59,60],常温常压下超硬的立方结构(金刚石和cBN)相对于层状六方结构(石墨和六方氮化硼)是亚稳相.如果进一步考虑尺寸效应,随着显微组织特征尺寸下降到几个纳米,立方结构和层状六方结构的相对稳定性将发生反转[22,61,62],常温常压下立方结构变成了稳定相.纳米孪晶极硬材料热稳定性的提高正是来自于此.

最近的第一性原理计算分析了纳米孪晶金刚石和cBN的变形行为和应力响应[63,64].研究表明,维氏压头产生的应力限域机理抑制了金刚石的石墨化和化学键的塌陷倾向.孪晶界的存在能够促进应力集中,从而驱动化学键择优重排,并导致断裂应变增大、峰值应力和刚性系数的二次增强.其中纳米孪晶金刚石和cBN的峰值剪切应力分别可达200 GPa和120 GPa.这些结果从塑性变形角度更加深入地理解了纳米孪晶结构的硬化机理.

4 压痕硬度测试原理

在这一节中,我们来讨论超高硬度测量这个大家普遍关心的重要问题:纳米孪晶金刚石的硬度已达到200 GPa,如何能够用硬度只有60—100 GPa的金刚石单晶压头可靠地测量出如此高的硬度?传统的观念认为比金刚石更硬的材料的硬度无法测量[8].直观地想像,要可靠测量一个材料的硬度,压头的硬度一定要大于被测样品的硬度,这里我们把这一可靠性判据称为硬度比较判据.众所周知,材料的压痕硬度被定义为压头施加的载荷除以被测样品表面留下的永久性压痕的接触面积(HV)或投影面积(HK)[65].也就是说,压痕硬度是一个被清晰定义的工程参量,只要能在被测样品表面留下塑性变形产生的永久性压痕并且金刚石压头没有可见的塑性变形发生,所测的材料压痕硬度值就是可靠的.例如维氏硬度通过HV(GPa)=1854.4L/2的公式来计算,其中L为施加的载荷,单位为牛顿;¯d为压痕两条对角线的平均长度(图4),单位为微米,一般通过安装在硬度仪上的光学显微镜测量所得.这样,压痕硬度如何能被可靠测量这一问题就归结为在什么条件下样品表面能够形成永久性压痕这样一个问题[66].

图4 维氏压头的压入过程,红线代表着多晶材料中的滑移系,位错用⊥表示,d1和d2为压痕的对角线长度,虚线表示被测样品表面的基准面位置[66]Fig.4.Indentation process with a Vickers indenter.Red lines schematically represent the slipsystems in the polycrystals with d islocations ind icated by⊥.d1andd2showthe diagonals of the formed indentation.The dashed lineemphasizes the basalplane of the sample surface[66].

当金刚石压头严格垂直地压入被测样品表面时,考虑到压头的对称性,压头相对的两个面的受力情况如图4所示:平行于样品表面的两个力(F2和F)相互抵消,压头因此只承受垂直方向的压应力(F1和F).这样,金刚石压头就处在一个压应力场中.无论水平方向的力有多大,都不会引起金刚石压头的塑性变形或断裂,只有当垂直方向的压应力超过金刚石的压缩强度时,压头才会断裂,硬度测量才失去意义.另一方面,压痕是样品表面塑性变形后留下的永久性痕迹,而材料塑性变形来自于位错运动.在压头压入样品表面的过程中,一旦应力集中超过了样品的剪切强度,位错开始沿滑移面运动、增殖并导致塑性变形后形成压痕.因此,压痕形成的判据应该是:金刚石压头的压缩强度大于样品的剪切强度,而不是过去认为的金刚石压头的硬度大于样品的硬度.我们在这里把该判据称之为强度比较判据.金刚石的理想压缩强度在最弱的〈100〉方向为220 GPa, 而在〈110〉和〈111〉方向约为470 GPa[67];大家知道,金刚石是自然界已知材料中剪切强度最高的材料,其理想剪切强度仅为93 GPa[68].因此,用金刚石作为压头,压痕的形成条件是自然满足的.由此我们可以得出这样的结论,用金刚石做压头可以测量出比自身还硬材料的硬度,包括纳米孪晶金刚石.

由上可见,比天然金刚石更硬材料的硬度能够被可靠地测量.如何评估硬度测量误差也是一个重要的问题.超硬材料最常用的硬度标度是维氏硬度.维氏硬度测量误差主要来自于压痕对角线长度的确定.理想对角线长度为压痕在样品表面基准面上相对两个顶点之间的距离(图5(c)中的d0).对于纳米孪晶金刚石这样的既硬又韧的材料,在硬度测量过程中通常会在压痕周围形成高于样品基准面的不均匀凸起.在这种情况下,光学显微镜测量的对角线长度(图5(c)中的d)就大于理想对角线长度,从而低估了实际的硬度值.我们可以使用原子力显微镜(AFM)对压痕对角线长度进行精确测量[69].图5对极硬的纳米孪晶金刚石样品在9.8 N载荷下所形成的压痕做了这样的修正.光学测量的压痕对角线平均长度为9.75µm,由此计算出的名义维氏硬度值为191.1 GPa;对同一个压痕,AFM精确测量的平均对角线长度为8.80µm,对应的硬度值为234.6 GPa.说明压痕对角线的平均值被高估了约10.8%,硬度测量值被低估了约18.5%(43.5 GPa).无论如何,测得的纳米孪晶金刚石硬度都远高于金刚石单晶压头的硬度.值得指出的是,为了给出可靠的硬度值,硬度测量过程中必须要避免压头的尺寸效应[70].在小载荷情况下,压头顶端刚开始压入样品,会在附近的样品区域产生很高的应变梯度,从而导致硬度测量值虚高.随着载荷的增大,硬度会趋于一个固定值,被称之为渐近线硬度.严格地讲,我们必须采用渐近线硬度来比较不同材料的硬度高低,这样得出的结论才是可靠的.

图5 纳米孪晶金刚石样品在9.8 N载荷下所形成压痕的AFM修正[66](a)AFM测量结果,插图显示了该压痕的光学显微镜照片,通过光学显微镜测量对角线长度的位置用青色方框标记;(b)对应(a)中直线的AFM轮廓线;(c)周围带有凸起的压痕剖面图Fig.5.AFMcalib ration of an indentation formed on a nanotwinned d iamond sample under a load of 9.8 N[66]:(a)AFMimage,the inset shows an optical microscope photograph of the same indentation where the cyan box emphasizes the position for indentation diagonals under the opticalmicroscope;(b)the line profi les correspond ing tothe colored lines in(a);(c)schematic diagramof the diagonal profi le across twoopposite corners of an indentation with pile-upridge.

5 展 望

纳米孪晶极硬材料的成功合成是超硬材料研究的一次突破.我们的研究为研发高性能超硬材料打开了一条技术途径,有望带来机械加工业和高压科学研究领域的新变革.未来的研究方向主要有:1)进一步提高纳米孪晶极硬材料的各项性能指标;2)探索高性能纳米孪晶极硬材料的规模化合成途径,制备出厘米尺寸的块材,满足应用需求;3)通过纳米结构化将传统的硬性材料提升为超硬材料,扩大超硬材料家族成员.在这里,我们简单介绍两类关于纳米孪晶极硬材料应用的前瞻性研究.

一代工具材料往往会派生出一代新技术.纳米孪晶极硬材料优异的性能、超细的显微组织结构特别适用于超精密切削加工.我们将纳米孪晶cBN块材加工成一个微刀具用于车削淬硬钢[71].实验结果表明经纳米孪晶cBN微刀具车削的淬硬钢,表面粗糙度在7 nm以下,实现了镜面切削加工.纳米孪晶极硬材料刀具适用于红外光学元件的超精密切削加工、硬质合金工件的高效切削加工和超精密切削加工、难于磨削加工的非球面工件和元件的超精密切削加工等.纳米孪晶极硬材料的出现,有望带来加工技术的新变革,在很多情况下都可实现以切代磨甚至超精密切削加工.

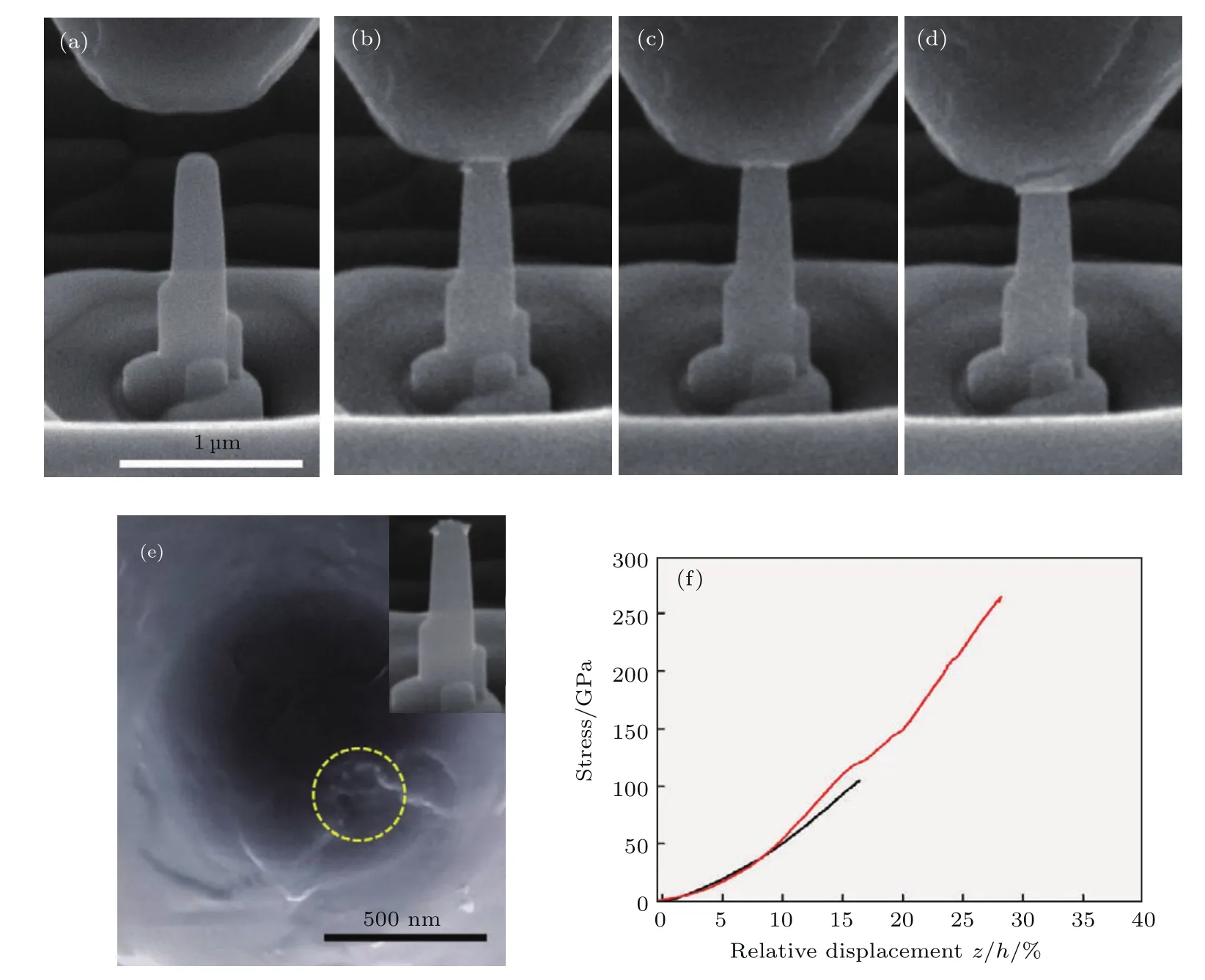
图6 纳米孪晶金刚石的单轴压缩实验 (a)—(d)单轴压缩实验中金刚石压头压向纳米孪晶金刚石纳米柱的过程;(e)实验结束后金刚石压头明显劈裂,而纳米孪晶金刚石纳米柱未见损坏;(f)根据纳米孪晶金刚石纳米柱顶部直径计算的应力-应变关系Fig.6.Uniaxial compression experiment on nanotwinned diamond:(a)–(d)The process of the d iamond fl at punch pushing towards the nanopillar of nanotwinned d iamond;(e)the fl at punch d iamond is obviously cleaved and fractured after themeasurement,while the nanotwinned diamond nanopillar is intact;(f)stressstrain relationships were calcu lated using the d iameter of the pillar apex of nanotwinned diamond pillar.

我们还初步研究了纳米孪晶金刚石的单轴压缩行为.用聚焦离子束(FIB)加工的纳米孪晶金刚石纳米柱直径约为200 nm.如图6所示,当压力超过120 GPa,纳米柱压入金刚石压头,直至270 GPa,金刚石压头被压出一个深坑后解理断裂,而纳米孪晶金刚石纳米柱在压入前后未见明显变化.这一结果明显优于金刚石单晶.金刚石单晶微柱的单轴压缩实验显示出明显的各向异性,〈100〉和〈111〉取向的金刚石单晶微柱分别在120 GPa和240 GPa时发生断裂[72].此外当压力超过120 GPa时,金刚石单晶微柱与金刚石压头接触的部位会发生非晶化,形成非晶层,而纳米孪晶金刚石样品则未见此现象发生.现阶段,用天然金刚石单晶做成的金刚石一级对顶砧可以达到的压力趋近400 GPa[73],被广泛用于地球科学和高压物理研究中.我们的单轴压缩实验结果表明,纳米孪晶金刚石非常适合制作金刚石对顶砧,有望实现500 GPa—1 TPa的超高压.这样的超高压力能够为探索新材料、验证理论预言、揭开像金属氢[74]这样的科学之谜提供必要的实验条件.

[1]Kanyanta V 2016Hard,Superhard and Ultrahard Materials:AnOverviewin: Kanyanta V (Ed.)Microstructure-Property Correlations for Hard,Superhard,and Ultrahard Materials(Cham:Springer International Pub lishing)p1

[2]Bundy F P,Hall HT,Strong HM,Wentorf R H1955Nature176 51

[3]W entorf R H1957J.Chem.Phys.26 956

[4]W estraad t J E,Sigalas I,Neeth ling J H2015In t.J.Refract.Met.Hard Mater.48 286

[5]Intensifying Manu factu ring Activity to Boost Demand for Superhard Materials 2014 G lobal Industry Analysts,Inc.http://www.strategy r.com/Superhard_Materials_Market_Report.asp[2016-10-10]

[6]Brookes C A,Brookes E J 1991D iamond Relat.Mater.1 13

[7]Brazhkin V V,Lyapin AG,Hemley R J 2002Philos.Mag.A82 231

[8]Brazhkin V,Dubrovinskaia N,Nicol M,Novikov N,Riedel R,SolozhenkoV,ZhaoY 2004Nat.Mater.3 576

[9]Chaudh ri MM,LimY Y 2005Nat.Mater.4 4

[10]Huang Q,Yu D,Xu B,Hu W,Ma Y,W ang Y,ZhaoZ,W en B,He J,Liu Z,Tian Y 2014Nature510 250

[11]GaoF M,He J L,W u E D,Liu SM,Yu D L,Li D C,Zhang S Y,Tian Y J 2003Phys.Rev.Lett.91 015502

[12]Simunek A,Vackar J 2006Phys.Rev.Lett.96 085501

[13]Li KY,W ang X T,Zhang F F,Xue D F 2008Phys.Rev.Lett.100 235504

[14]Dubrovinskaia N,Solozhenko V L,Miya jima N,Dmitriev V,Ku rakevych OO,Dubrovinsky L 2007Appl.Phys.Lett.90 101912

[15]Irifune T,KurioA,SakamotoS,Inoue T,Sumiya H2003Nature421 599

[16]Dubrovinskaia N,Dub S,Dub rovinsky L 2006NanoLett.6 824

[17]SolozhenkoV L,Ku rakevych OO,Le Godec Y 2012Adv.Mater.24 1540

[18]Tian Y,Xu B,Yu D,Ma Y,W ang Y,Jiang Y,Hu W,Tang C,GaoY,LuoK,ZhaoZ,Wang L M,W en B,He J,Liu Z 2013Nature493 385

[19]Haines J,Leger J M,Bocquillon G 2001Annu.Rev.Mater.Res.31 1

[20]Veprek S 2013J.Vac.Sci.Technol.A31 050822

[21]Tian Y,Xu B,ZhaoZ 2012In t.J.Refract.Met.Hard Mater.33 93

[22]ZhaoZ,Xu B,Tian Y 2016Annu.Rev.Mater.Res.46 383

[23]Yeung MT,Mohammad iR,Kaner R B2016Annu.Rev.Mater.Res.46 465

[24]Teter D M1998MRS Bu ll.23 22

[25]Liu AY,Cohen ML 1989Science245 841

[26]G ilman J J 1973Hardness—AStrength Microprobein:W estb rook J H,Con rad H(Ed.)The Science of Hardness Testing and its Research Applications(Metals Park:American Society for Metals)

[27]Phillips J C 1970Rev.Mod.Phys.42 317

[28]Sangiovanni D G,Hu ltman L,Chirita V 2011Acta Mater.59 2121

[29]Ivanovskii AL 2012Prog.Mater.Sci.57 184

[30]GuoX,Li L,Liu Z,Yu D,He J,Liu R,Xu B,Tian Y,W ang HT2008J.Appl.Phys.104 023503

[31]Ceder G 1998Science280 1099

[32]Li C,Li J C,Jiang Q 2010Solid State Commun.150 1818

[33]G lass CW,Oganov AR,Hansen N 2006Comput.Phys.Commun.175 713

[34]W ood ley SM,CatlowR 2008Nat.Mater.7 937

[35]W ang Y C,LüJ,Zhu L,Ma Y M2010Phys.Rev.B82 094116

[36]AmslerM,Goedecker S 2010J.Chem.Phys.133 224104

[37]Pickard C J,Needs R J 2011J.Phys.:Condens.Matter23 053201

[38]Lonie D C,Zu rek E 2011Comput.Phys.Commun.182 372

[39]Zhang X,W ang Y,LüJ,Zhu C,Li Q,Zhang M,Li Q,Ma Y 2013J.Chem.Phys.138 114101

[40]Hall E O1951Proc.Phys.Soc.London B64 747

[41]Petch N J 1953J.Iron Steel Ins.174 25

[42]Y ipS 2004Nat.Mater.3 11

[43]Tse J S,Klug D D,GaoF M2006Phys.Rev.B73 140102

[44]Halperin W P 1986Rev.Mod.Phys.58 533

[45]Khan MAM,Kumar S,Ahamed M2015Mater.Sci.Semicond.Process.30 169

[46]Chang Y K,Hsieh HH,Pong W F,Tsai MH,Chien F Z,Tseng P K,Chen L C,Wang TY,Chen KH,Bhusari D M,Yang J R,Lin S T1999Phys.Rev.Lett.82 5377

[47]Gerberich W W,Mook W M,Perrey C R,Carter C B,Baskes MI,Mukherjee R,G idwani A,Heberlein J,Mc-Murry P H,G irshick S L 2003J.Mech.Phys.Solids.51 979

[48]Dubrovinskaia N,Dubrovinsky L,Crichton W,Langenhorst F,Richter A2005Appl.Phys.Lett.87 083106

[49]Liu G D,Kou Z L,Yan X Z,Lei L,Peng F,Wang Q M,W ang KX,W ang P,Li L,Li Y,LiW T,W ang Y H,Bi Y,Leng Y,He D W 2015Appl.Phys.Lett.106 121901

[50]Tanigaki K,Ogi H,Sumiya H,Kusakabe K,Nakamura N,HiraoM,Ledbetter H2013Nat.Commun.4 2343

[51]Sumiya H,HaranoK2012D iamond Relat.Mater.24 44

[52]Sumiya H,HaranoK,Irifune T2008Rev.Sci.Instrum.79 056102

[53]Dubrovinsky L,Dubrovinskaia N,Prakapenka V B,Abakumov AM2012Nat.Commun.3 1163

[54]Sumiya H,Irifune T2007J.Mater.Res.22 2345

[55]Lu L,Chen X,Huang X,Lu K2009Science323 607

[56]Lu L,Shen Y F,Chen X H,Qian L H,Lu K2004Science304 422

[57]Lu K,Lu L,Su resh S 2009Science324 349

[58]Shan ZW,Lu L,Minor AM,Stach E A,MaoSX 2008JOM60 71

[59]Bundy F P,Bassett W A,W eathers MS,Hemley R J,MaoHU,Goncharov AF 1996Carbon34 141

[60]SolozhenkoV L,Tu rkevich V Z,HolzapfelW B1999J.Phys.Chem.B103 2903

[61]Hu S L,Yang J L,Liu W,Dong Y G,CaoS R,Liu J 2011J.Solid State Chem.184 1598

[62]Yang C C,Li S 2008J.Phys.Chem.C112 1423

[63]Li B,Sun H,Chen C 2014Nat.Commun.5 4965

[64]Li B,Sun H,Chen C 2016Phys.Rev.Lett.117 116103

[65]Meyer E 1908Z.Ver.D tsch.Ing.52 645

[66]Xu B,Tian Y J 2015J.Phys.Chem.C119 5633

[67]LuoX,Liu Z,Xu B,Yu D,Tian Y,W ang HT,He J 2010J.Phys.Chem.C114 178501

[68]Roundy D,Cohen M2001Phys.Rev.B64 212103

[69]Jensen C P,Jorgensen J F,Garnaes J,PicottoG B,Gori G 1998J.Test.Eval.26 532

[70]N ix W D,GaoH1998J.Mech.Phys.Solids46 411

[71]Chen J,Jin T,Tian Y 2016Sci.China:Technol.Sci.59 876

[72]W heeler J M,Raghavan R,W ehrs J,Zhang Y,Erni R,Mich ler J 2016NanoLett.16 812

[73]Dalladay-Simpson P,Howie R T,G regoryanz E 2016Nature529 63

[74]Ashcroft N W 1968Phys.Rev.Lett.21 1748

PACS:62.20.–x,81.07.Bc,61.72.MmDOI:10.7498/aps.66.036201

High pressu re syn thesis of nanotwinned u ltrahard materials∗

Xu Bo Tian Yong-Jun†

(State Key Laboratory ofMetastab le Materials Science and Technology,Yanshan University,Qinhuangdao066004,China)(Received 10 October 2016;revised manuscript received 24 October 2016)

In this review,we present our recent research progress in superhard materials,with specially focusing on twotopics.One topic is tounderstand hardnessmicroscopically and estab lish the quantitative relationshipbetween hardness and atomic parameters of crystal,which can be used toguide the design of novel superhard crystals.The other topic is toidentify the fundamental principle and technologicalmethod toenhance the comprehensive performances(i.e.,hardness,fracture toughness,and thermal stability)of superhard materials,and tosynthesize high-performance superhard materials.Starting fromthe chemicalbonds associated with crystalhardness and electronic structure,we propose amicroscopic understanding of the indentation hardness as the combined resistance of chemical bonds in a material toindentation.Under this assumption,we establish themicroscopic hardnessmodel of covalent single crystals and further generalize it topolycrystalline materials.According tothe polycrystalline hardnessmodel,we successfully synthesize nanotwinned cubic boron nitride and diamond bu lks under high pressure and high temperature.Thesematerials exhibit simultaneous improvements in hardness,fracture toughness,and thermal stability.We alsoclarify a long-standing controversy about the criterion for performing a reliab le indentation hardnessmeasurement.Our research points out a newdirection for developing the high-performance superhard materials,and promises innovations in both machinery processing industry and high pressure science.

superhard materials,Hall-Petch effect,quantumconfinement eff ect,nanotwins

10.7498/aps.66.036201

∗国家自然科学基金(批准号:51525205,51421091,51332005)和河北省杰出青年基金(批准号:E2014203150)资助的课题.

†通信作者.E-mail:fhcl@ysu.edu.cn

*Project supported by the National Natural Science Foundation of China(G rant Nos.51525205,51421091,51332005)and the Natu ral Science Foundation for D istinguished Young Scholars of Hebei Province of China(G rant No.E2014203150).

†Corresponding author.E-mail:fhcl@ysu.edu.cn