反馈控制棘轮的定向输运效率研究∗

范黎明 吕明涛 黄仁忠 高天附† 郑志刚

1)(沈阳师范大学物理科学与技术学院,沈阳 110034)2)(华侨大学信息科学与工程学院,厦门 361021)(2016年6月7日收到;2016年9月30日收到修改稿)

反馈控制棘轮的定向输运效率研究∗

范黎明1)吕明涛1)黄仁忠1)高天附1)†郑志刚2)

1)(沈阳师范大学物理科学与技术学院,沈阳 110034)2)(华侨大学信息科学与工程学院,厦门 361021)(2016年6月7日收到;2016年9月30日收到修改稿)

研究了反馈耦合布朗棘轮中粒子处于负载力、时变外力及噪声作用下的定向输运问题.详细讨论了外力作用时间的不对称性、外势空间的不对称性及外力周期等对反馈耦合棘轮中粒子输运效率的影响.研究发现,外力的时间不对称度能促进反馈棘轮中粒子的定向输运,随时间不对称度的增大,反馈棘轮中粒子能获得较大的效率.然而,外势空间的不对称度能有效抑制耦合棘轮中粒子的扩散,达到增强耦合粒子定向输运的效果.同时还发现,存在最优的噪声强度能使耦合粒子的输运效率达到最大.

反馈控制,时空不对称性,定向输运,能量转化效率

1引 言

从热运动环境中获取能量一直是人类的梦想.根据热力学第二定律,当系统处于热力学平衡态时,定向输运是不可能产生的.由此可知若系统的时空对称性破缺(非对称周期势[1,2]、非对称周期力[3]、噪声作用[4−7]等)才会产生定向输运.棘轮系统正是这样一种处于非平衡态并能产生定向输运的系统[8−10].为了研究系统的定向输运,人们提出了各种布朗棘轮模型[11−13].通过分析布朗粒子的运动情况,可清晰地了解棘轮系统中粒子的定向输运特性[14].所得理论结果在实验上还可应用于提高纳米量级分子马达的性能[15−18].

目前,有关棘轮中粒子的输运性能已得到广泛研究.如Ai等[19]研究了外力频率对定向输运的影响,发现外力频率能影响布朗马达的运动方向.除了外力作用,负载力不仅会降低分子马达的输运能力,而且还会使肌球蛋白VI在接触位点的平均驻留时间呈指数增长[20].更为有趣的是耦合作用也会促进粒子的定向输运,当单个布朗粒子陷于势阱底部并处于大阻尼时,不能形成定向输运.然而当考虑多粒子耦合时,粒子可跨越势垒并能产生输运现象[21].在生物体内部的定向输运过程中,正是这种耦合作用促进了分子马达的输运性能[22].因此,研究耦合作用能够帮助我们获得马达系统的定向输运能力[23].此外,棘轮系统的优化控制也是研究粒子间合作定向输运的重要方面.通过不断对开环控制策略进行改进,文献[24—28]提出了依赖于系统状态的闭环控制方法.实验上这种控制方式的实现是通过监测溶液中胶体粒子任一时刻的状态来决定外势的打开或关闭[29].这种控制方式不仅可为分子马达的步进机理及效率做出解释[30−32],而且还可优化棘轮技术[33].因此我们将结合实验上的这种控制方法进一步研究反馈耦合布朗棘轮中粒子的定向输运性能.

近年来,关于布朗棘轮中粒子定向输运性能的研究虽已取得很多突破性的进展[34,35],但是反馈耦合棘轮中粒子的能量转化效率了解得并不是十分清楚.因此分析耦合粒子的能量转化效率对深入了解耦合作用下的反馈控制棘轮中粒子的输运特性也是非常必要的.研究效率问题不仅帮助我们从能量角度了解棘轮系统中粒子的输运性能,还可清晰地获得棘轮系统中粒子对输入能量的利用率[36].目前实验上已发现分子马达的能量转化效率很高,有的甚至接近百分之百,而现有理论计算得到的结果与马达实际的效率相比还有很大差距[37].因此,理论上找到影响效率的关键因素,并对此进行优化来提高棘轮系统中粒子对输入能量的有效利用率至关重要.棘轮系统中粒子的能量转化效率越高,说明定向输运的性能越理想.

为全面了解反馈棘轮中粒子的定向输运性能,本文采用含负载力、时变外力的反馈耦合布朗棘轮模型,研究外势的空间不对称性、外力的时间不对称性及外力作用周期等对耦合布朗粒子的平均速度、扩散及能量转化效率的影响.结果发现:随外力的时间不对称度的增加,反馈棘轮中粒子的速度、扩散及效率的最优值均随之增大;为提高系统中粒子的输运性能,本文还详细讨论了反馈耦合棘轮中粒子的效率,同时所得结论可为纳米机器动力系统效率的提高起到理论指导作用[38].需要指出的是,在某一外力作用周期下,存在合适的外势空间不对称度能使反馈棘轮中粒子的输运性能达到最大.

2模 型

本文主要研究过阻尼下的耦合布朗粒子.受非对称周期势U(xi)、非对称周期外力F(t)、反馈控制ε(t)、负载力λ及噪声的作用,其动力学行为可由过阻尼朗之万方程描述[39,40]:

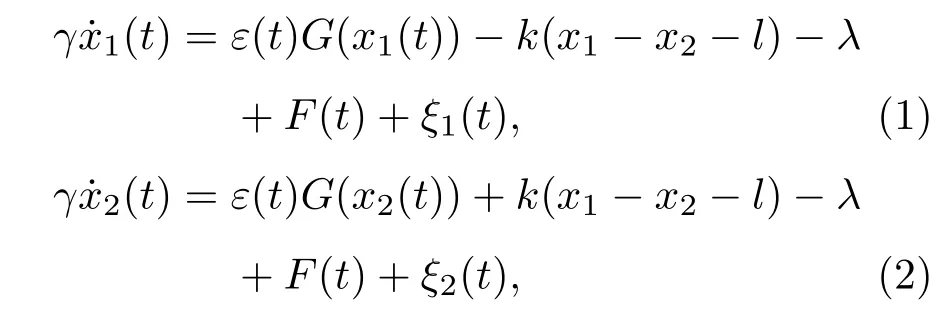
其中,两个耦合布朗粒子在t时刻的位置分别表示为x1(t)和x2(t);γ为介质的阻尼系数;考虑粒子间的相互作用为弹性耦合,且弹性系数为k,自然长度为l;λ为布朗粒子受到的负载力;F(t)为t时刻耦合布朗粒子受到的非对称周期外力,如图1所示.

图1中A表示周期外力的振幅,τ为外力作用时间的周期.一个周期内,A的作用时间为τ1,−A的作用时间为τ2,当τ1= τ2时,正、负外力会相互抵消,当τ1̸= τ2时,总的外力效果会产生一个净力[3]. 用σt(σt= τ1/τ2)表示外力作用时间的不对称度.由此可知外力作用时间的不对称度越大,说明一个周期内A的作用时间就越长,相同时间内向耦合棘轮中粒子输入的能量也越多.此外,ξ1(t)与ξ2(t)为高斯白噪声,且满足〈ξi(t)〉=0,〈ξi(t)ξj(t)〉=2Dδijδ(t− t′), 其中D为噪声强度.方程中G(xi(t))表示粒子受到棘轮势的作用,具有如下关系:

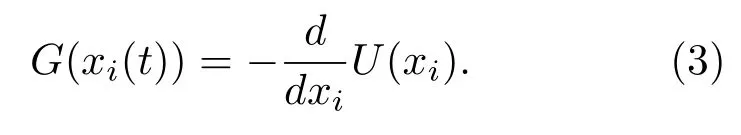
U(xi)为周期外势,其表述如下,

其中d表示势垒高度,如图(2)所示.本文采用棘轮势的周期L=1.外势的不对称系数可表示为σs=c/(L−c)(0＜c＜L),反映棘轮势空间的不对称程度.因此σs可决定棘轮势的结构.

图1 非对称周期外力示意图Fig.1.The schematic diagram of asymmetric periodic external force.

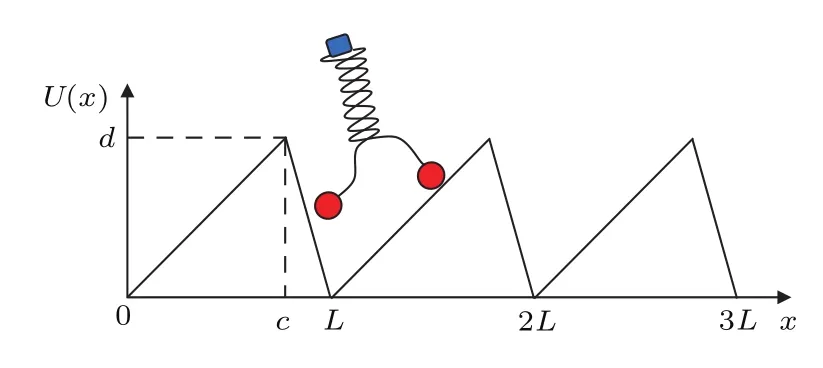
图2 耦合布朗棘轮结构示意图Fig.2.The schematic diagram of coupled Brownian ratchets.

方程(1),(2)中ε(t)为控制棘轮势打开或关闭的开关.如果布朗粒子受到外势的平均作用大于零,那么耦合棘轮处于打开的状态(ε(t)=1),如果受到外势的平均作用小于或等于零,耦合棘轮处于关闭的状态(ε(t)=0),所以控制开关ε(t)可表示为

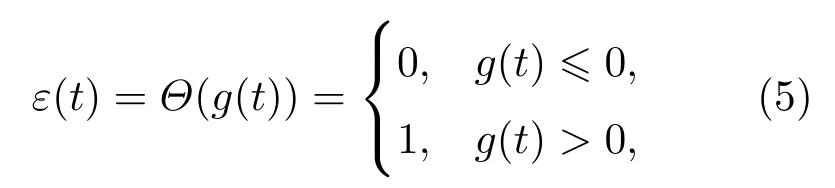
其中Θ为亥维赛函数,g(t)表示耦合布朗粒子在棘轮势中受到的平均作用力,即

因此方程(1)和(2)表示为受反馈控制的耦合布朗粒子运动方程.

为了研究耦合布朗粒子的定向输运,本文计算了耦合布朗粒子质心的平均速度.其表达式如下[36,41]:

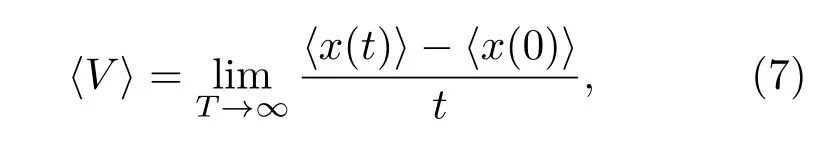
其中,〈·〉表示系综平均.由于耦合布朗粒子会发生扩散现象,因此引入平均有效扩散系数Deff来描述粒子质心位移的涨落,其表达式如下[34]:

式中,T为耦合粒子的演化时间.对于反馈耦合棘轮来说,仅知道耦合粒子质心的平均速度和扩散还不足以对反馈棘轮中粒子的定向输运性能进行全面了解,因此本文还将重点讨论耦合棘轮中粒子的能量转化效率η,其表达式如下[23]:

其中,〈Vi〉为粒子的平均速度.该效率表示为一定时间内耦合棘轮中粒子克服负载所做的有用功与外力输入到系统的总能量之比.需要注意的是,采用(9)式计算效率时,如果外力F(t)很小,分母中由外力输入到系统的总能量也会很小,此时数值计算的结果会有一定波动.

本文采用随机龙格-库塔算法对方程(1)和(2)进行数值计算.为了获得稳定的系综平均值,计算时模拟5×103条轨道,每个轨道演化50个周期,其中时间步长h=10−3.文中所有物理量均采用无量纲化处理,无特殊说明参量取γ=1.0,l=0.4,L=1.0,d=2.5.

3结果与讨论

3.1 外力振幅的影响

图3(a)为不同外力作用时间的不对称度σt下耦合布朗棘轮中粒子质心的平均速度随外力振幅A的变化关系曲线.从图中可发现存在一个最优振幅强度能使耦合粒子的定向输运达到最大.当时间不对称度σt逐渐增大时,耦合棘轮中粒子质心平均速度的最大值也会随之增大,且粒子质心达到最大速度时所需的最优振幅逐渐减小.这是因为随着σt的增大,每个周期内施加在耦合棘轮中粒子正向力的作用时间增加,这样即使在较小的外力振幅作用下由外力输入到耦合棘轮中粒子的总能量也会增大,这样耦合粒子越过势垒形成定向运动的概率增加,促使耦合布朗棘轮中粒子质心的平均速度变大.

图3(b)给出了改变外力作用时间的不对称度σt时,外力振幅A对耦合棘轮中粒子质心的平均有效扩散系数的影响.研究发现,当振幅达到某一合适值时,耦合粒子质心的平均有效扩散系数会达到一个最大值.然而,随着时间不对称度σt的增加,平均有效扩散系数的最大值也会随之增大,且最大值对应的最优振幅强度会随之减小.说明外力作用时间的不对称度对耦合粒子质心的扩散同样能起促进作用.

为了更好地研究反馈棘轮中粒子定向输运的性能,本文还探讨了外力作用时间的不对称度σt对棘轮中粒子能量转化效率的影响,结果如图3(c)所示.需要说明的是,采用(9)式计算效率,当外力振幅很小时,分母所示的由外力输入到系统中粒子的总能量将趋于零.此时数值计算的效率会很大,结果会导致图像有一定的波动,所以在不影响分析反馈棘轮中粒子输运性能的前提下我们的振幅取值如图3(c)所示.可以发现棘轮中粒子效率不是外力振幅A的单调函数,且存在振幅的最优值能使耦合棘轮中粒子的效率达到最大.因为当外力输入的能量足以驱动粒子跨越势垒形成定向运动后,如果再继续增大振幅输入更多的能量,此时耦合粒子并不能对输入的全部能量进行有效利用,从而导致能量转化效率降低.总体来看,当外力作用时间的不对称度σt增大时,反馈棘轮中粒子的能量转化效率也会随之增大,且效率最大值所对应的最优振幅强度逐渐减小.如当σt=9.0时,可利用较小的外力振幅就能使反馈棘轮中粒子获得较大的输运效率.说明外力作用时间的不对称度能促进反馈控制棘轮中粒子的能量转化.

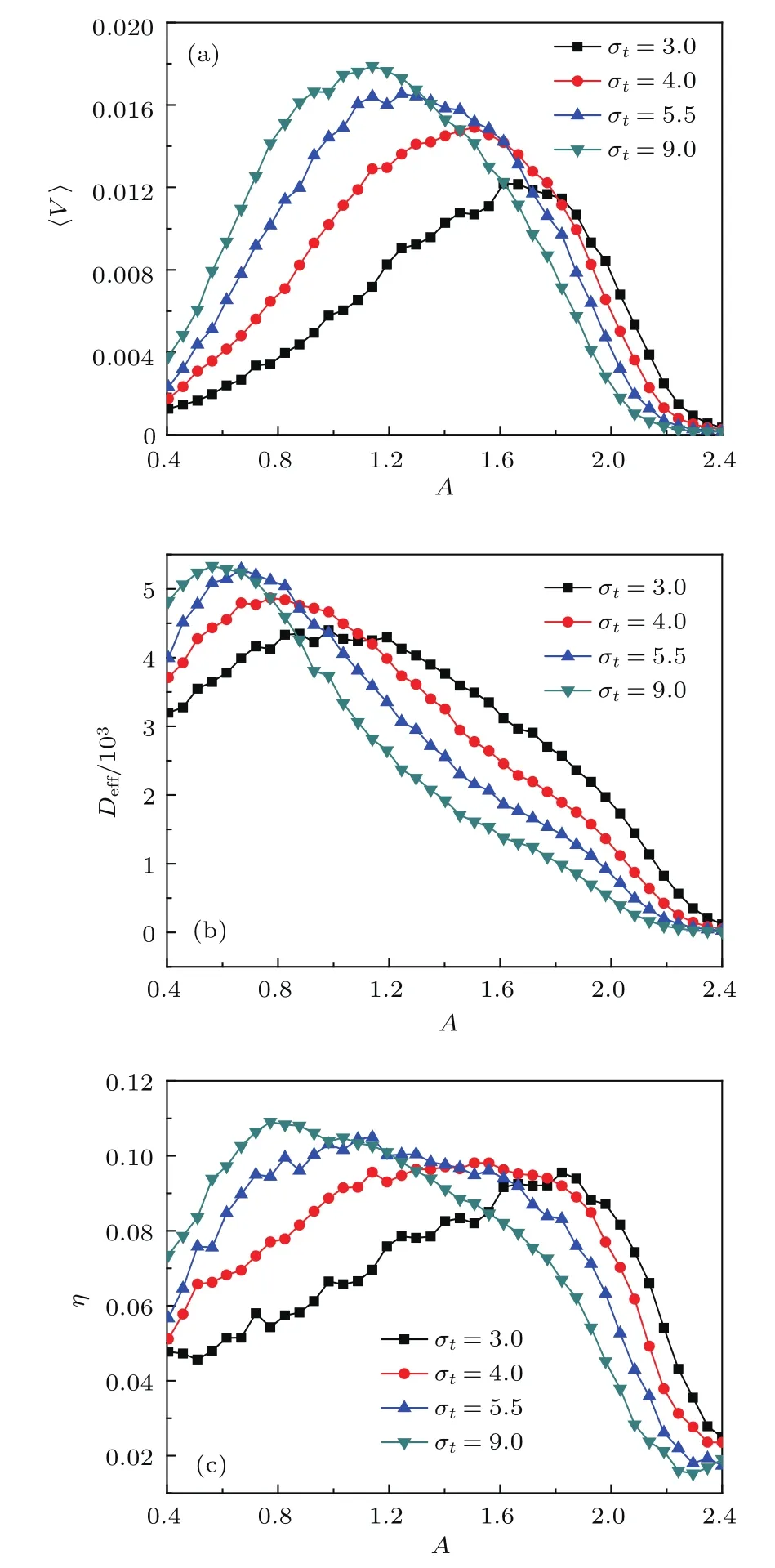
图3 (网刊彩色)(a)平均速度〈V〉,(b)平均有效扩散系数Deff和(c)能量转化效率η随外力振幅A的变化曲线,其中D=0.01,k=1.0,λ=5.0,σs=0.96,τ=10Fig.3.(color online)The curves of(a)the centerof-mass velocity 〈V 〉,(b)the average effective diffusion coefficient Deffand(c)the energy conversion effi ciency η varying with the amplitude of external force A,where D=0.01,k=1.0,λ =5.0,σs=0.96,τ=10.

3.2 外力作用周期的影响

图4(a)给出了不同外势不对称系数σs下,耦合棘轮中粒子质心的平均速度随外力作用周期τ的变化关系.从图中可发现,在外力作用周期不太大时,耦合布朗粒子质心的平均速度呈准周期变化,且当外力周期较小时速度的波动很大,这是因为当外力作用周期较小时,外力振幅A方向变化的频率较快,因此会导致耦合粒子受力不稳定,所以速度图像振荡较明显;然而当外力作用周期较大时,外力振幅A方向变化的频率较慢,因此粒子受力趋于稳定且平均速度波动较小.研究还发现,随着外力周期的变化,外势的不对称度对反馈棘轮中粒子定向输运的影响也发生改变.如在较小的外力周期下,当σs=0.7时耦合棘轮中粒子的定向输运最强.而当外力周期增大时,如τ＞1.0,最优的外势不对称度变为0.65.因此可通过选取合适的外势空间不对称度和外力周期来共同促进反馈棘轮中粒子的定向输运.

图4(b)给出了在不同的外势不对称系数σs下耦合粒子质心的平均有效扩散系数随外力作用周期τ的变化关系曲线.研究发现,耦合布朗粒子质心的平均有效扩散系数随外力作用周期τ也呈准周期变化,随着外力周期τ的增加,耦合粒子质心有效扩散系数变化的幅度逐渐变小,说明此时耦合棘轮中粒子的定向输运逐渐增强;然而随着外势不对称度σs的增加,我们发现耦合棘轮中粒子质心扩散的幅度随之降低,说明利用较大的空间不对称度能够有效地抑制反馈棘轮中粒子质心的扩散,达到增强耦合系统中粒子定向输运的效果.

为了更清晰地了解反馈耦合棘轮中粒子的输运性能,本文还进一步讨论了外力作用周期τ对系统中粒子能量转化效率的影响,得到的结果如图4(c)所示.研究发现,耦合棘轮中粒子效率的变化同粒子平均速度的变化趋势一样不会随着外力周期τ呈单调变化.当外力作用周期较小时,方向变化频率较为频繁,大部分能量都消耗在F(t)方向的频繁转变上,因此用来跨越势垒的能量较少;当外力作用周期较大时,F(t)方向变化的频率降低,此时耦合粒子会利用更多的能量来跨越势垒并形成定向输运.此外,研究还发现,当外势空间的不对称度σs等于0.4或0.7时,随着周期τ的增加,棘轮系统中粒子能量转化效率逐渐趋于稳定;然而当外势空间的不对称度相对较小如σs等于0.55或0.65时,随着外力作用周期的增加,耦合棘轮中粒子的效率仍在增大.说明较小的外势空间不对称度对反馈控制棘轮中粒子效率的提高具有促进作用.

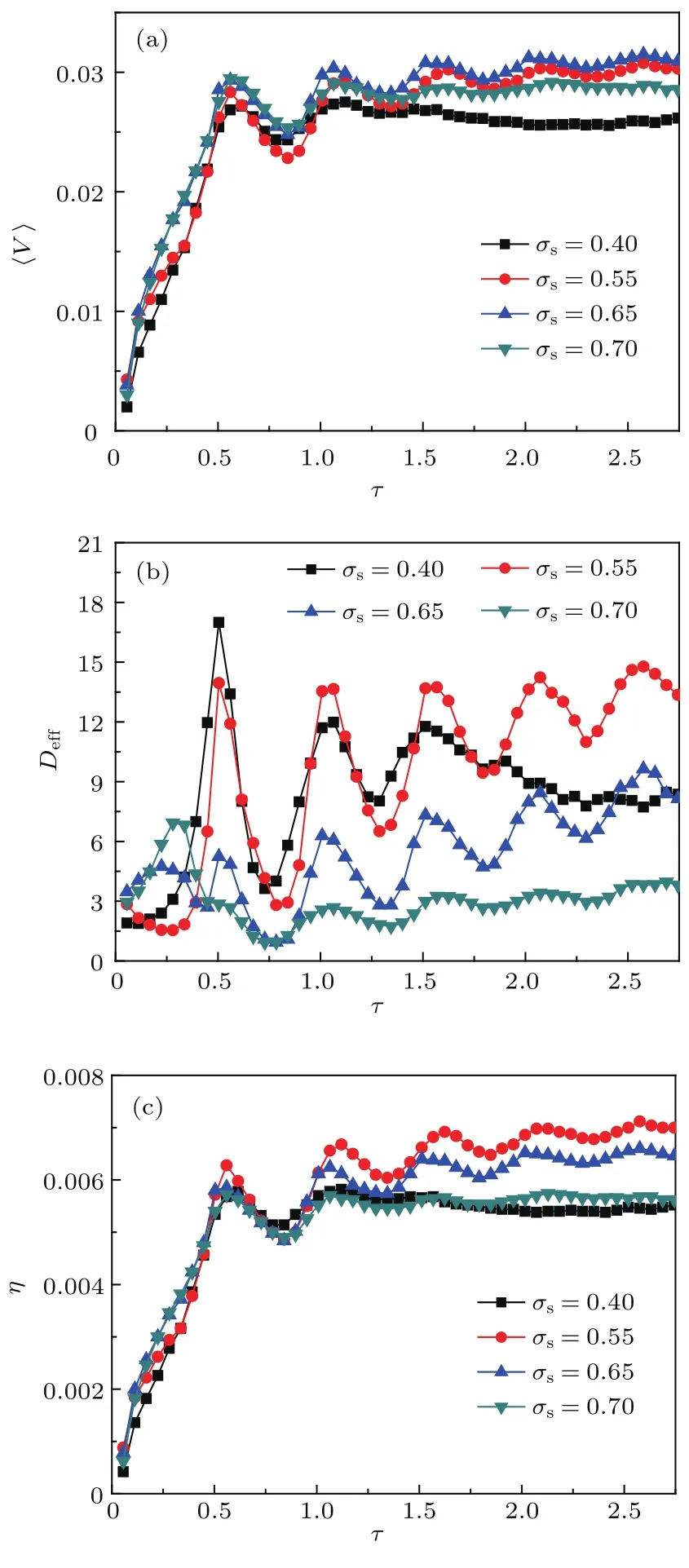
图4 (网刊彩色)(a)平均速度〈V〉,(b)平均有效扩散系数Deff和(c)能量转化效率η随外力周期τ的变化曲线,其中D=0.01,k=0.1,A=3.75,λ=2.0,σt=0.8Fig.4.(color online)The curves of(a)the center-ofmass velocity 〈V 〉,(b)the average e ff ective di ff usion coefficient Deffand(c)the energy conversion efficiency η varying with the period of external force τ,where D=0.01,k=0.1,A=3.75,λ =2.0,σt=0.8.

3.3 噪声的影响

图5(a)给出了不同弹簧劲度系数k下耦合布朗棘轮中粒子质心的平均速度随噪声强度D的变化关系.可以发现,在不同的弹簧劲度系数k下,都会存在一个最优的噪声强度D使反馈棘轮中粒子质心的平均速度达到最大.此外,随着弹簧劲度系数k的增大,耦合棘轮中粒子质心达到最大速度时的最优噪声强度也随之增加.这是因为随着耦合粒子相互作用的增强,粒子不容易越过势垒形成定向运动.因此随着k的增加,耦合棘轮中粒子需要较大的噪声强度来促进耦合粒子越过势垒,从而形成定向输运.这也说明噪声在耦合棘轮中的作用并不总是阻碍系统中粒子的定向输运.此外,当噪声强度D很大时,不同弹簧劲度系数下的棘轮中粒子质心速度趋于一致.说明当系统的噪声很强时粒子完全在做自由扩散运动,粒子间的相互作用对耦合系统中粒子的定向输运不再起作用.

图5(b)为不同弹簧劲度系数k下反馈棘轮中粒子质心的平均有效扩散系数与噪声强度D的关系曲线.研究发现,同样存在合适的噪声强度D使反馈棘轮中粒子质心的平均有效扩散系数达到最大.说明在耦合棘轮中,噪声并不总是促进耦合布朗粒子的自由扩散.此外,随着弹簧劲度系数k的增大,Deff的最大值也随之增大,说明对于耦合布朗粒子,在一定条件下耦合强度也能促进反馈控制棘轮中粒子的扩散.然而,当噪声强度D很大时,不同劲度系数k下的有效扩散趋于一致,说明此时噪声占据主导作用,耦合粒子在做自由扩散运动.

为了更详细地研究耦合棘轮中粒子的定向输运性能,图5(c)进一步研究了不同弹簧劲度系数k下反馈棘轮中粒子能量转化效率随噪声强度D的变化关系.研究发现,同样存在最优的噪声强度D能使反馈棘轮中粒子的效率达到最大.因为当噪声很弱时,棘轮中粒子热运动不明显,因此粒子很难越过势垒形成定向输运;然而在较大噪声强度下,粒子完全在做自由扩散,同样不利于形成定向输运.同时还发现,当噪声强度D非常弱时,利用较小的劲度系数能使棘轮系统中粒子获得较大的效率;而当噪声强度D很大时,不同劲度系数下反馈棘轮中粒子的能量转化效率趋于一致.说明当耦合粒子完全在做自由扩散运动时,劲度系数对耦合棘轮中粒子能量转化的影响不再明显.也就是说,利用合适的热涨落和粒子间的相互作用同样可提高反馈控制棘轮中粒子的能量转化效率.

图5 (网刊彩色)(a)平均速度〈V〉,(b)平均有效扩散系数Deff和(c)能量转化效率η随噪声强度D的变化A=3.75,λ =2.0,σt=0.8,σs=0.96,τ=10Fig.5.(color online)The curves of(a)the centerof-mass velocity 〈V 〉,(b)the average e ff ective diffusion coefficient Deffand(c)the energy conversion efficiencyηvarying with the noise intensity D,where A=3.75,λ =2.0,σt=0.8,σs=0.96,τ=10.

4结 论

本文研究了处于负载力、时变外力及噪声作用下反馈耦合布朗棘轮中粒子的定向输运性能.详细分析了外势的空间不对称性、外力的时间不对称性、外力周期及噪声强度对耦合布朗粒子质心的平均速度、扩散及棘轮系统中粒子能量转化效率的影响.研究发现,外力的时间不对称度能促进反馈棘轮中粒子的定向输运,且在不同的时间不对称度下,耦合布朗粒子质心的平均速度、平均有效扩散系数及能量转化效率均能达到最优值.同时,在不同的空间不对称度下,棘轮中粒子质心的平均速度、扩散及系统中粒子能量转化效率随着外力周期的增加呈准周期变化.此外,合适的噪声强度也能促进反馈棘轮中粒子的输运效率.上述结论可应用于渗透、粒子分离与提高分子马达的效率等方面,对微观尺度下生物纳米器件的研制具有一定的理论指导作用.

[1]Mateos J L 2000 Phys.Rev.Lett.84 258

[2]Barbi M,Salerno M 2000 Phys.Rev.E 62 1988

[3]Sumithra K,Sintes T 2001 Physica A 297 112

[4]Hanggi P,Marchesoni F 2009 Rev.Mod.Phy.81 387

[5]Zheng Z G 2004 Spantiotemporal Dynamics and Collective Behaviors in Coupled Nonlinear System(1st Ed.)(Beijing:Higher Education Press)pp278–340(in Chinese)[郑志刚2004耦合非线性动力系统的时空动力学与合作行为 (第一版)(北京:高等教育出版社)第278—340页]

[6]Machura L,Kostur M,Luczka J 2010 Chem.Phys.375 445

[7]Mielke A 2000 Phys.Rev.Lett.84 818

[8]Doering C R 1995 Nuovo Cimento 17 685

[9]Jülicher F,Ajdari A,Prost J 1997 Rev.Mod.Phys.69 1269

[10]Astumian R D,Bier M 1994 Phys.Rev.Lett.72 1766

[11]Xie P 2010 Int.J.Biol.Sci.6 665

[12]Reimann P 2002 Phys.Rep.361 57

[13]Rozenbaum V M,Yang D Y,Lin S H,Tsong T Y 2006 Physica A 363 211

[14]Wang H Y,Bao J D 2003 Physica A 323 197

[15]Linke H 2002 Appl.Phys.A:Mater.Sci.Process.75 167

[16]van den Heuvel M G L,Dekker C 2007 Science 317 333

[17]Braun O M,Kivshar Y S 1998 Phys.Rep.306 1

[18]Landa P S,McClintock P V E 2000 Phys.Rep.323 1

[19]Ai B Q,He Y F,Zhong W R 2011 Phys.Rev.E 83 051106

[20]Li C P,Han Y R,Zhan Y,Hu J J,Zhang L G,Qu J 2013 Acta Phys.Sin.62 230051(in Chinese)[李晨璞,韩英荣,展永,胡金江,张礼刚,曲蛟 2013物理学报 62 230051]

[21]Chen H B,Zheng Z G 2011 Mod.Phys.Lett.B 25 1179

[22]Downton M T,Zuchermann M J,Craig E M,Plischke M,Linke H 2006 Phys.Rev.E 73 011909

[23]Wang H Y,Bao J D 2007 Physica A 374 33

[24]Feito M,Cao F J 2006 Phys.Rev.E 74 041109

[25]Feito M,Cao F J 2007 Eur.Phys.J.B 59 63

[26]Feito M,Cao F J 2007 Phys.Rev.E 76 061113

[27]Feito M,Cao F J 2008 Physica A 387 4553

[28]Gao T F,Chen J C 2009 J.Phys.A:Math.Theor.42 065002

[29]Rousselet J,Salome L,Ajdari A,Prost J 1994 Nature 370 446

[30]Bier M 2007 Biosystems 88 301

[31]Zhang H W,Wen S T,Chen G R,Li Y X,Cao Z X,Li W 2012 Chin.Phys.B 21 038701

[32]Bustamante C,Chemla Y R,Forde N R,Izhaky D 2004 Annu.Rev.Biochem.73 705

[33]Cao F J,Feito M,Touchette H 2009 Physica A 388 113

[34]Wang L F,Gao T F,Huang R Z,Zheng Y X 2013 Acta.Phys.Sin.62 070502(in Chinese)[王莉芳,高天附,黄仁忠,郑玉祥2013物理学报62 070502]

[35]Qin T Q,Wang F,Yang B,Luo M K 2015 Acta Phys.Sin.64 120501(in Chinese)[秦天齐,王飞,杨博,罗懋康2015物理学报64 120501]

[36]Wang H Y,Bao J D 2005 Physica A 357 373

[37]ZhaoA K 2007M.S.Dissertation (Zhengzhou:Zhengzhou University)(in Chinese)[赵阿可 2007硕士学位论文(郑州:郑州大学)]

[38]Derényi I,Astumian R D 1999 Phys.Rev.E 59 R6219

[39]Bao J D 2012 An Introduction to Anomalous Statisticl Dynamics(1st Ed.)(Beijing:Science Press)pp127–184(in Chinese)[包景东2012反常统计动力学导论第一版(北京:科学出版社)第127—184页]

[40]Li G,Tu Z C 2016 Sci.China:Phys.Mech.Astron.59 640501

[41]Zheng Z G,Cross M C,Hu G 2002 Phys.Rev.Lett.89 154102

PACS:05.40.–a,05.40.Jc,02.30.YyDOI:10.7498/aps.66.010501

*Project supported by the National Natural Science Foundation of China(Grand Nos.11475022,11347003)and the Scienti fi c Research Funds of Huaqiao University and the Excellent Talents Program of Shenyang Normal University,China(Grand No.91400114005).

†Corresponding author.E-mail:tianfugao@synu.edu.cn

Investigation on the directed transport efficiency of feedback-control ratchet∗

Fan Li-Ming1)Lü Ming-Tao1)Huang Ren-Zhong1)Gao Tian-Fu1)†Zheng Zhi-Gang2)

1)(College of Physical Science and Technology,Shenyang Normal University,Shenyang 110034,China)2)(College of Information Science and Engineering,Huaqiao University,Xiamen 361021,China)(Received 7 June 2016;revised manuscript received 30 September 2016)

Brownian motion in the environment of the thermal fl uctuations is a long-study issue in nonequilibrium statistical physics.In recent years,the directed transport properties of Brownian ratchets attract the widespread attention of scholars.When a ratchet system possesses the spatio-temporal symmetry-breaking feature,the directed transport can be produced.Although the breakthrough progress in the directed transport of the Brownian ratchet has been made,the energy conversion efficiency of feedback ratchet is not clear.Therefore,the center-of-mass mean velocity and the energy conversion efficiency of coupled ratchet under the in fl uences of the time asymmetry of external force and the spatial asymmetry of external potential are discussed in detail.

The overdamped coupled Brownian particles are investigated.Nevertheless,the optimized control of the coupled ratchet is the important for directed transport.Therefore,the closed-loop control which depends on the state of the system is adopted.The dynamic behavior of coupled particles can be described by the overdamped Langevin equation,and the equation is numerically solved by using the stochastic Runge-Kutta algorithm.Some properties of the directed transport can be obtained through this method,such as the center-of-mass mean velocity,the energy conversion efficiency,etc.

It is interesting to fi nd that the center-of-mass mean velocity can reach a maximum as the amplitude of external force increases.However,the mean velocity can show the quasi-periodic oscillations with the increase of the period of external force for di ff erent values of the spatial asymmetry of external potential.In addition,it can be found that the feedback ratchet needs strong noise to make the directed transport of the ratchet reach the maximum as the coupled strength increases.On the other hand,the energy conversion efficiencies of the feedback ratchet can achieve their corresponding maximum values with the increase of the amplitude of external force for di ff erent values of the time asymmetry,and the maximum increases as the time asymmetry increases.However,the efficiency can also show the quasi-periodic oscillations with the increase of the period of the external force for di ff erent values of the spatial asymmetry of external potential.Moreover,the energy conversion efficiency can achieve the maximum as the noise strength increases,but the maximum of the efficiency will decrease with the increase of coupling strength.From the discussion above,the optimal values of the time asymmetry,the spatial asymmetry,the period of the external force and the noise strength can promote the directed transport of the feedback coupled Brownian ratchet.These conclusions can provide some guidance in the enhancement of the energy conversion efficiency of a nanomachine.

feedback control,spatio-temporal asymmetry,directed transport,energy conversion efficiency

10.7498/aps.66.010501

∗国家自然科学基金(批准号:11475022,11347003)、华侨大学科研启动费项目和沈阳师范大学优秀人才支持计划(批准号:91400114005)资助的课题.

†通信作者.E-mail:tianfugao@synu.edu.cn