弱测量对四个量子比特量子态的保护∗

黄江

(广东海洋大学电子与信息工程学院,湛江 524088)(2016年8月11日收到;2016年9月14日收到修改稿)

弱测量对四个量子比特量子态的保护∗

黄江†

(广东海洋大学电子与信息工程学院,湛江 524088)(2016年8月11日收到;2016年9月14日收到修改稿)

廖湘萍等(Chin.Phys.B 23 020304,2014)指出弱测量和弱测量反转操作可以保护三个量子比特的纠缠,提高保真度.本文将弱测量方法推广至四个量子比特的情况,研究了几种典型四个量子比特量子态的演化.结果表明：在振幅阻尼通道中,弱测量方法能够有效地提高系统量子态的保真度.分析了影响量子态保真度的各种因素,对比了不同量子态的演化特征,划分了量子态保真度提高的敏感区域.最后,对弱测量方法抑制量子态衰减的内在机制做了合理的物理解释.

弱测量,四量子比特,振幅阻尼,保真度

1引 言

量子态可以得出量子体系的所有性质[1].作为量子力学的基本假定之一,量子态及其演化一直是研究者们关注的对象.量子态可分为纠缠态和可分离态,纠缠态的概念由爱因斯坦等[2]引入.随着量子理论的深入和实验水平的提高,量子纠缠[3−12]这种纯粹的量子效应已经得到了验证.量子纠缠不仅仅是区分量子与经典现象的重要依据,也是量子信息和量子计算的关键资源.随着量子信息技术的发展,量子纠缠因其优越的特性而得到了广泛的研究.众所周知,任何真实的量子系统都可以认为是开放系统,相互作用环境会不可避免地影响系统的纠缠,从而导致退相干,甚至出现纠缠猝死[13−16].如何有效地保护系统的相干性成为研究者们关注的课题.目前,关于系统相干性[17−28]的理论研究取得了长足的进步,部分研究成果已经进入实用阶段,中国研发的世界首颗量子通信卫星便是其代表性成果.

Korotkov等[29,30]提出了一种全新的抑制量子系统退相干的方法——弱测量与弱测量反转,能够使一个超导相位量子态在振幅阻尼通道中得以概率性地恢复.这种方法有效地增强了量子态抑制退相干的能力,虽然其结果是概率性的,但此方法却为抑制退相干提供了一个全新的处理思路.弱测量是在冯·诺依曼测量和半正定算子值测量(POVM)的基础上发展出来的一种部分坍缩测量.弱测量从量子系统中提取的信息比较有限,能够有效防止测量系统的量子态随机地坍缩至其本征态.因此,在适当的操作下可以将量子态以一定的概率反转至其初始态.自弱测量方法提出以来,与此相关的实验和理论工作均得到了迅速发展.随着研究的深入,各种性质逐步明确,诸多应用也受到了高度的关注.实验上,利用弱测量方法来抑制退相干已经在固体系统[31]、线性光学系统[32−34]和超导相位比特[35,36]中成功实现.弱测量的理论工作也取得了丰硕成果,Korotkov和Keane[37]提出了一种利用量子反转测量来抑制单量子比特零温环境下的退相干方案;Wang等[38]提出了一种在较低温度环境中利用弱测量方法来保护单量子比特退相干的方法;Sun等[39]提出了利用弱测量及弱测量反转的方法来保护低维量子系统的纠缠;Kim等[40]在理论和实验上均证明了在振幅阻尼通道中弱测量方法能够有效保护两个量子比特的纠缠;近期,Xiao和Li[41]以及Liao等[42]将弱测量方案推广至两体三能级和三体二能级系统.

然而,目前关于四体二能级原子系统量子态保护的研究工作并不多.由于四体二能级原子系统的基矢有16个,演化时会生成16×16的密度矩阵.因此,四体系统的计算量较大,讨论会更加复杂.另外,四体二能级系统的度量还没有统一的判据,这也增加了研究的难度.幸运的是,本文得到了在振幅阻尼衰减通道中四体二能级系统保真度的解析解,划分了保真度保护的区域.通过引入保真度提高的概念,对比弱测量前后的结果,得到了四体二能级系统的保真度在大部分情况下都能得到有效保护的结论.本文对弱测量抑制退相干的物理机制也做了相应的解释.本文的安排如下：第二部分给出与本文相关的基础理论;第三部分研究弱测量对初始处于纠缠态和可分离态的几种典型的四体二能级原子保真度的影响;最后,对本文作简单的总结.

2基础理论

2.1 振幅阻尼

振幅阻尼通道[3]是描述量子系统与环境相互作用耗散过程的一个重要模型,在开放量子系统中有着诸多应用.在Born-Markov近似下,可以用Kraus算符来模拟单量子比特的演化过程:

其中ρ(0)和ρ(t)分别表示量子态初始时刻和任意时刻的密度矩阵,Ei(i=1,2)为Kraus算符,

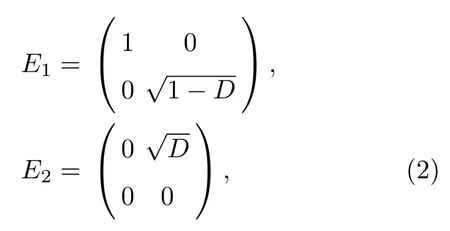
D为衰减率,取值范围为D∈[0,1].Kraus算符满足完备性关系根据方程(1)和方程(2),可以得到四个量子比特的演化

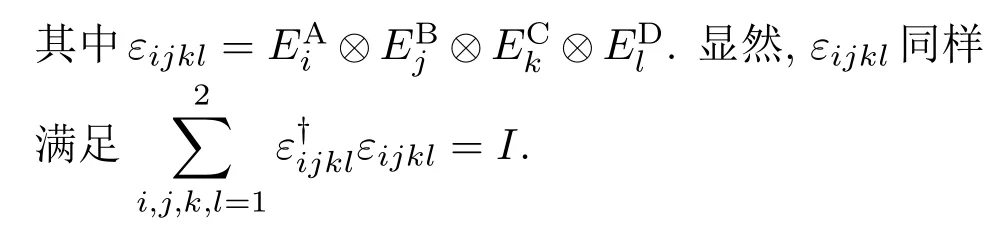
2.2 保真度

为了度量在相互作用过程中输出量子态与输入量子态的接近程度,引入保真度[43]的概念:

其中,F∈[0,1],|ψin〉为相互作用之前的初始输入量子态,ρout表示相互作用后的输出量子态.保真度的值越高,表示系统的量子态保持得越完整.反之,则衰减得越严重.保真度是衡量两量子态接近程度的物理量,不仅可以度量输入态为纠缠态的情况,也适用于输入态为可分离态的情形.因此,对于纠缠态而言,保真度在一定程度上能够反映纠缠的演化、衰减及保护情况.本文将分别对这两类量子态进行研究.

2.3 弱测量及弱测量反转

四个量子比特的弱测量和弱测量反转过程[40,42]可以表示为

其中Mwk(p1,p2,p3,p4)为弱测量算符,p1,p2,p3,p4分别为弱测量强度;Mrev(pr1,pr2,pr3,pr4)表示弱测量反转算符,pr1,pr2,pr3,pr4分别为弱测量反转强度.由于两个算符Mwk、Mrev均为非幺正算符,操作的成功率因而小于1.弱测量操作能使输入量子态以一定的概率跃迁至基态,减少了振幅阻尼的影响,而弱测量反转则可使输出量子态恢复至初始输入量子态.因此,理论上前置弱测量和后置弱测量操作可以起到削弱振幅阻尼衰减、保护系统量子态的效果.文献[40]已经证明：当弱测量反转强度取时,系统的量子态能够得到最大程度的保持.为了计算方便,本文取此最佳值.同时,假设四个量子比特是全同的,即p=p1=p2=p3=p4,pr=pr1=pr2=pr3=pr4.方程(5)和(6)可写成如下较为简洁的形式

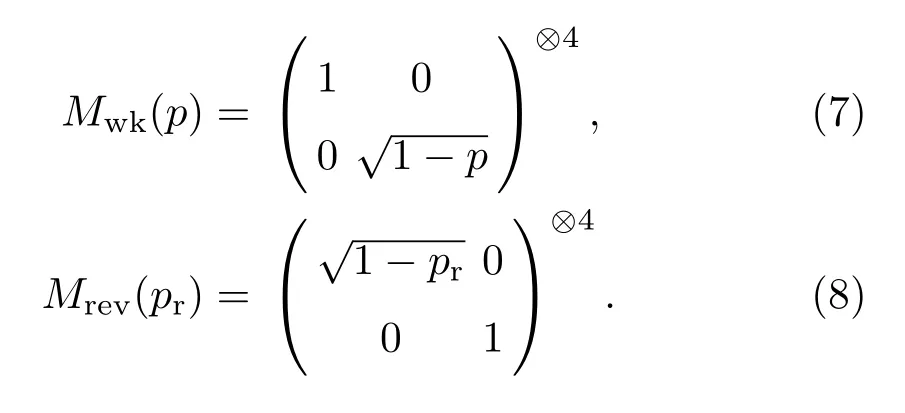
3四个量子比特量子态的保护

本节阐述论文的核心思想,将详细研究弱测量前后几种典型的四个量子比特量子态在振幅阻尼通道中的保真度.通过对比,得到量子态保真度的演化规律,划分保真度提高区域,并解释其物理原因.首先介绍弱测量的实验方案图,如图1所示.实验方案分为三个步骤：第一步,在初始制备的四比特量子态上执行弱测量操作,激发态将概率性的跃迁至基态;第二步,将弱测量后的量子态通过振幅阻尼通道,系统的退相干在此过程中发生;第三步,再对此量子态执行弱测量反转操作,以一定的概率将量子态恢复至初态,从而实现了量子态的保护.

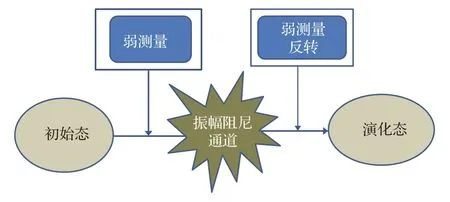
图1 四量子比特弱测量保护的实验方案图Fig.1.Experiment schemes for protecting four-qubit using weak measurement and quantum weak measurement reversal.

3.1 输入态为纠缠态

3.1.1 Greenberger-Horne-Zeilinger(GHZ)态考虑初始量子态为GHZ态[44]的情况首先,GHZ态直接经历振幅阻尼衰减通道,用ρG表示四个量子比特在此过程中的演化量子态,则

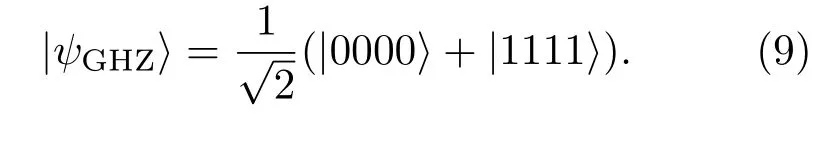
选取基矢{|abcd〉},其中a,b,c,d=0,1.由于矩阵ρG较大,此处只给出非零的密度矩阵元:

结合方程(4),很容易计算GHZ态直接通过振幅阻尼衰减通道的保真度

接下来对GHZ态执行弱测量操作,即：弱测量+振幅阻尼+弱测量反转.用ρG(WM),ρG(AD)和ρG(WR)分别表示四个量子比特弱测量、振幅阻尼和弱测量反转过程中的演化量子态

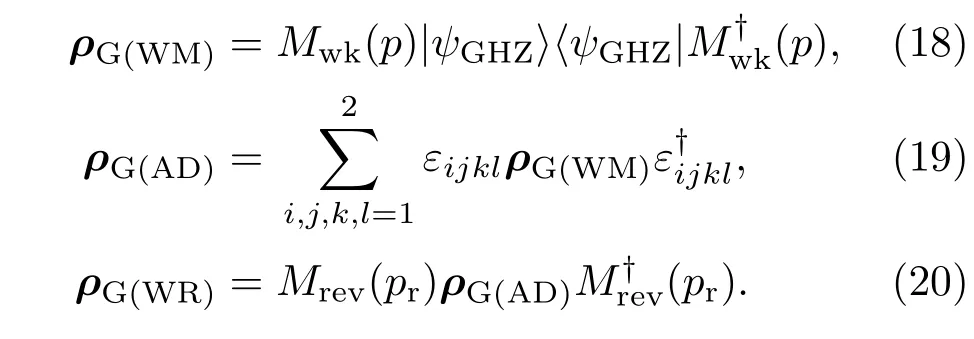
整理ρG(WR)的计算结果,并归一化处理后,得到如下非零的矩阵元:

其中C1=(1−pr)4+(1−p)4[(1−D)+D(1−pr)]4为归一化因子.计算弱测量后的保真度为

为了更直观地表示弱测量对保真度的保护效果,引入保真度提高[45]的概念

图2给出了弱测量前后保真度随参数D和p变化的曲面,其中两个曲面相交的曲线表示F(ρG(WR))=F(ρG). 由图可以看出,对于GHZ态而言,弱测量并不是在任何时候都能提高保真度,而是在一定区域范围内成立.图3进一步说明了这一点,参考平面以上区域为保真度可以得到提高的区域,平面以下则反之.图2和图3清晰地划分了弱测量提高保真度的区域,为GHZ纠缠态的制备、演化、弱测量等方面的研究提供了理论依据.

图2 (网刊彩色)GHZ态的保真度随参数D和p的演化曲面,其中红色曲面表示弱测量后的F,绿色曲面表示弱测量前的FFig.2.(color online)The fidelity of GHZ states is plotted against the parameters D and p.The red curve respects F after weak measurement,and the green curve is the F before weak measurement.

图3 (网刊彩色)GHZ态的保真度提高随参数D和p的演化曲面,其中红色曲面表示Fimp,绿色曲面表示零参考面Fig.3.(color online)The fidelity improvement of GHZ states is plotted against the parameters D and p.The red curve respects Fimp,and the green curve is zero reference plane.

3.1.2 W态

用ρW表示W态直接通过振幅阻尼衰减通道的演化态,则

接下来研究W态[44]

经计算可得ρW的非零矩阵元:

容易计算振幅阻尼衰减W态的保真度为

接下来,做弱测量操作.计算过程较为复杂,此处不一一写出.归一化后的非零矩阵元为

其中C2=[(1−D)+D(1−pr)]为归一化因子.此时的保真度为

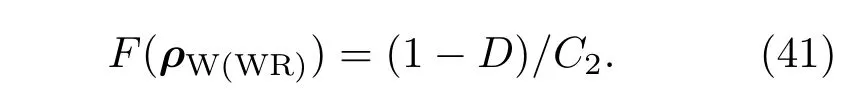
保真度提高为

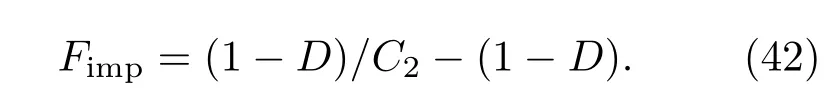
图4分别绘出了弱测量前后的保真度和弱测量保真度提高随参数D和p变化的演化图像.令人惊讶的是,与GHZ态不同,W态经过弱测量后保真度在任意情况下都高于弱测量操作之前,Fimp也因此恒大于0.由此证明,W态的弱测量在整个演化区域都能使保真度得到有效的保护,保护的效果与参数D和p的取值有关.D,p的取值越接近于1,保真度越能得到明显提高.将此结论与三体GHZ态和W态的演化规律[42]相比,可以发现两者的结论几乎是一致的,这也进一步证明了本文结论是可靠的.同时,可以推断此结论应该对四体以上的量子态的保真度也成立.当然,相关的证明会较为复杂.另外,三体与四体量子态弱测量演化特性的相似性表明初始制备量子态的结构对其保真度的演化起决定性影响.不同特性的纠缠态有着相互各异的演化规律.

图4 (网刊彩色)(a)W态弱测量前后的保真度F和(b)保真度提高FimpFig.4.(color online)(a)The fidelity F of W states before and after weak measurement,and(b)the fidelity improvement Fimp.

3.1.3 簇态(CL)

进一步研究四个量子比特CL态[46]的演化

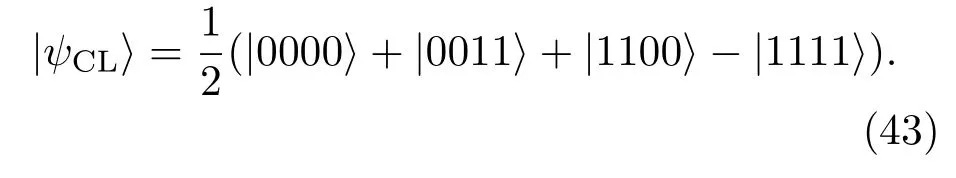
用ρC表示CL态直接经历振幅阻尼通道的演化态,类似于GHZ态和W态的步骤,容易解出CL态弱测量前的归一化非零矩阵元:

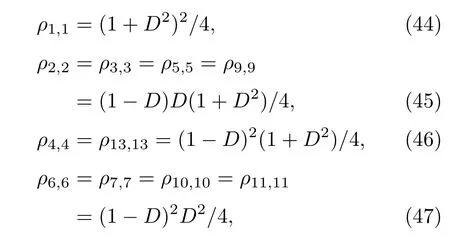
用ρC(WR)表示CL态弱测量后的演化态,由于CL态的弱测量非零矩阵元较为复杂,归一化因子表达式庞大,此处只给出弱测量反转强度pr取最佳值时的化简结果.

其中C3=1+2(D−Dp)+2(D−Dp)2+(D−Dp)3+(D−Dp)4/4为归一化因子.CL态弱测量的保真度及保真度提高分别为

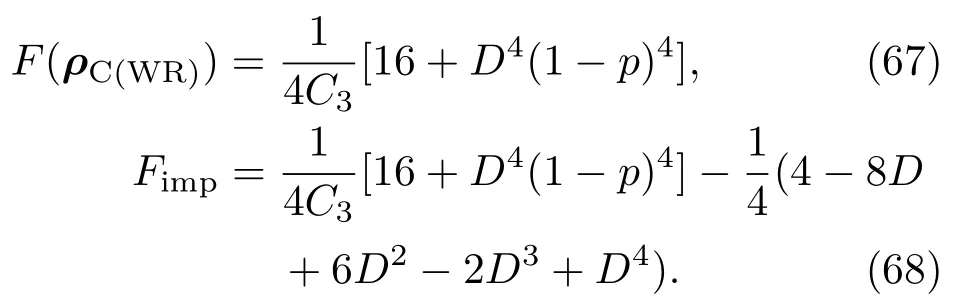
图5分别给出了CL态的保真度F(ρC(WR))和保真度提高Fimp随参数D和p的演化曲面.容易发现,与GHZ态和W态都不同的是,CL态在绝大部分区域保真度都能得到有效的提高,仅仅在D→1,p→0的极小区域衰减.由此可见,量子态的结构不同,弱测量对保真度的影响也各异.

图5 (网刊彩色)(a)CL态弱测量前后的保真度F和(b)保真度提高FimpFig.5.(color online)(a)The fidelity F of CL states before and after weak measurement,and(b)the fidelity improvement Fimp.

最后,简单地研究四体Dick态[44]|ψD〉=|1010〉).重复以上操作,容易证明,Dick态的弱测量规律类似与CL态,所不同的是保真度提高的区域略小而已.

3.2 输入态为可分离态

现在研究输入的四个量子比特为可分离态的弱测量方案.考虑四个全同量子比特,初始分别处于状态则系统的量子态可写为

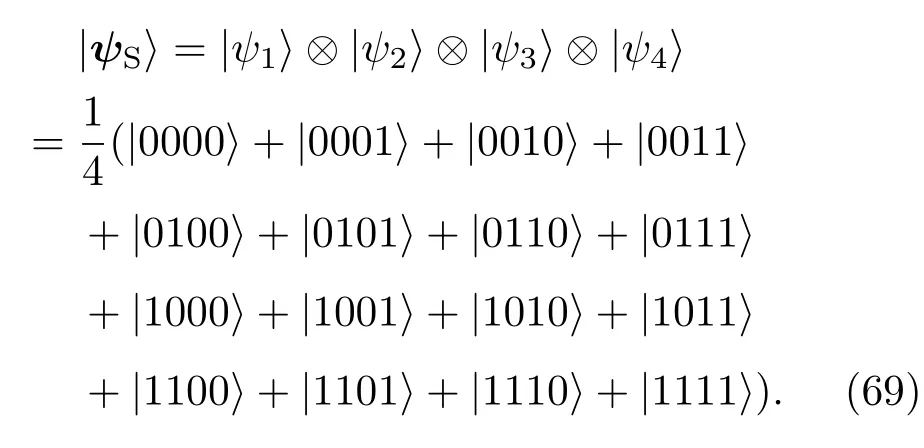
可分离态|ψS〉比较具有代表性,其构成的16×16个密度矩阵元均为非零值.其他量子态可在此基础上,通过调节归一化系数并取部分矩阵元得到.因此,本处只讨论此可分离态|ψS〉.由于处理方法与上一节类似,不难求解其演化密度矩阵元,得到弱测量前后的保真度和保真度提高的表达式.

图6 (网刊彩色)(a)可分离态弱测量前后的保真度F和(b)保真度提高FimpFig.6.(color online)(a)The fidelity F of separable states before and after weak measurement,and(b)the fidelity improvement Fimp.

图6表明,在振幅阻尼通道中弱测量方案下的保真度在全区域内都能得到有效的保护.保真度提高的量与参数D和p的取值有关.D,p越大,保护效果越佳.另外,对比纠缠态的弱测量,很容易发现|ψS〉的弱测量演化与W态的结果较为相似.经分析,将基矢做适当排列,W态密度矩阵的结构与|ψS〉一致,可以看成是 |ψS〉的一个分块矩阵,其他部分矩阵元为零,不参与演化,故两者之间的相似性也容易理解.由此进一步说明量子态的结构是弱测量保护效果的决定性因素.

依上述结论可知,弱测量方法对四能级原子任意形式量子态的保真度均能起到较明显的保护作用,其抑制量子态衰减的物理机制可解释如下：前置量子弱测量降低了激发态所占的权重,弱测量使得原子处于基态的概率越大.而基态原子在通过振幅阻尼通道时不受影响.最后,对量子态执行弱测量反转操作,重新恢复了激发态的权重,从而有效抑制了量子态在振幅阻尼通道中的衰减,起到了保护效果.需要说明的是,由于弱测量及弱测量反转为非幺正操作,因此本方法具有一定的成功概率.虽然弱测量方法无法做到百分百成功,但此方法所开辟的新思路对量子信息的发展有着深远的影响.到目前为止,已经验证了弱测量方法对四体及四体以下的量子态的相干性能起到保护作用.由其保护机制可以预言,弱测量方法对四体以上量子态的相干性依旧有保护效果.

4结 论

本文运用弱测量和弱测量反转研究了在振幅阻尼衰减通道中四量子比特量子态的保真度演化,分别得到了四个量子比特纠缠态和可分离态的保真度、保真度提高的解析表达式,绘制了演化曲面,讨论了各参数的影响,并划分了量子态保护的敏感区域.研究结果表明：量子态的结构是弱测量效果的决定性因素,不同结构的量子态对弱测量有着不同的反应.对于纠缠态,GHZ态的保真度在较大区域内能得到保护,W态在全区域内都能有效提高,而CL和Dick态则介于两者之间.当输入特定的四个量子比特可分离态时,由于其结构类似于W态,演化规律也与W态相似,进一步证明了量子态的结构对弱测量有着至关重要的影响.本文对四个量子比特量子态的弱测量做了初步研究,得到了保真度的一些性质,对多体量子系统的研究有一定的指导意义.

[1]Zhou S X 2002 Quantum Dynamics(Beijing:Higher Education Press)pp17–25(in Chinese)[周世勋 2002 量子力学 (北京:高等教育出版社)第17—25页]

[2]Einstein A,Podolsky B,Rosen N 1935 Phys.Rev.47 777

[3]Nielsen M A,Chuang I L 2002 Quantum Computation and Quantum Informatin(Cambridge:Cambridge University Press)pp74–89

[4]Zeng H F,Shao B,Yang L G,Li J,Zou J 2008 Chin.Phys.B 18 3265

[5]Sun G H,Aoki M A,Dong S H 2013 Chin.Phys.B 22 050302

[6]Yu T,Eberly J H 2007arXiv preprint arXiv:0707.3215

[7]Zhang R,Qin H,Tang B,Xue P 2013 Chin.Phys.B 22 100301

[8]Mazhar A,Alber G,Rau A R P 2009 J.Phys.B 42 025501

[9]Mazhar A,Guhne O 2014 J.Phys.B 47 055503

[10]Yu T,Eberly J H 2003 Phys.Rev.Lett.97 140403

[11]Simon C,Kempe J 2002 Phys.Rev.A 65 052327

[12]López C E,Romero G,Lastra F,Solano E,Reamal J C 2008 Phys.Rev.Lett.101 080503

[13]Yu T,Eberly J H 2002 Phys.Rev.B 66 193306

[14]Yu T,Eberly J H 2003 Phys.Rev.B 68 165322

[15]Yu T,Eberly J H 2004 Phys.Rev.Lett.93 140404

[16]Yang B Y,Fang M F,Huang J 2013 Chin.Phys.B 22 080303

[17]Pan J W,Gasparoni S,Ursin R,Weihs G,Zeilinger A 2003 Nature Phys.423 1014

[18]Xiao X,Fang M F,Li Y L,Zeng K,Wu C 2009 J.Phys.B:At.Mol.Opt.Phys.42 235502

[19]Huang J,Guo Y N,Xie Q 2016 Chin.Phys.B 25 0203032

[20]Zou H M,Fang M F 2016 Chin.Phys.B 25 090302

[21]Fan Z L,Ren Y K,Zeng H S 2016 Chin.Phys.B 25 010303

[22]Han W,Jiang K X,Zhang Y J,Xia Y J 2015 Chin.Phys.B 24 120304

[23]Mazhar A 2015 Chin.Phys.B 24 1203035

[24]Mazhar A,Huang J 2014 Chin.Phys.Lett.31 110301

[25]Wang Z L,Wang Z,Fan H Y 2015 Chin.Phys.B 24 1203016

[26]Yang Y B,Wang W G 2015 Chin.Phys.Lett.32 030301[27]Shan C J,Xia Y J 2006 Acta Phys.Sin.55 1585(in Chinese)[单传家,夏云杰 2006物理学报 55 1585]

[28]Zou Q,Hu X M,Liu J M 2015 Acta Phys.Sin.64 080302(in Chinese)[邹琴,胡小勉,刘金明 2015物理学报 64 080302]

[29]Korotkov A N 1999 Phys.Rev.B 60 5737

[30]Katz N,Neeley M,Ansmann M,Radoslaw C B,Hofheinz M,Lucero E,Connell A,Wang H,Cleland A N,Martinis J M,Korotkov A N 2008 Phys.Rev.Lett.101 200401

[31]Korotkov A N,Jordan A N 2006 Phys.Rev.Lett.97 166805

[32]Kim Y S,Cho Y W,Ra Y S,Kim Y H 2009 Opt.Express 17 11978

[33]Lee J C,Jeong Y C,Kim Y S,Kim Y H 2011 Opt.Express 19 16309

[34]Xu X Y,Kedem Y,Sun K,Vaidman L,Li C F,Guo G C 2013 Phys.Rev.Lett.111 033604

[35]Katz N,Ansmann M,Bialczak R C,Lucero E,Mcdermott R,Neeley M,Ste ff en M,Weig E M,Cleland A N,Martinis J M,Korotkov A N 2006 Science 312 1498

[36]Groen J P,Riste D,Tornberg L,Cramer J,Degroot P C,Picot T,Johansson G,Dicarlo L 2013 Phys.Rev.Lett.111 090506

[37]Korotkov A N,Keane K 2010 Phys.Rev.A 81 040103

[38]Wang S C,Yu Z W,Wang X B 2014 Phys.Rev.A 89 022318

[39]Sun Q Q,Amri M A,Zubairy M S 2009 Phys.Rev.A 80 033838

[40]Kim Y S,Lee J C,Kwon O,Kim Y H 2012 Nature Phys.8 117

[41]Xiao X,Li Y L 2013 Eur.Phys.J.D 67 204

[42]Liao X P,Fang M F,Fang J S,Zhu Q Q 2014 Chin.Phys.B 23 020304

[43]Schumacher B W 1996 Phys.Rev.A 54 2614

[44]Song X L,Yang M 2016 Acta Phys.Sin.65 080303(in Chinese)[宗晓岚,杨名 2016物理学报 65 080303]

[45]Xiao X,Feng M 2011 Phys.Rev.A 83 054301

[46]Jungnitsch B,Moroder T,Guhne O 2011 Phys.Rev.Lett.106 190502

PACS:03.65.Yz,03.65.Ud,03.67.MnDOI:10.7498/aps.66.010301

*Project supported by the natural science foundation of Guangdong province(Grant No.2015A030310354),and the Foundation of Excellent-Young-Backbone Teacher of Guangdong Ocean University,China.

†Corresponding author.E-mail:940038299@qq.com

The protection of qudit states by weak measurement∗

Huang Jiang†

(Electronic and Information Engineering College,Guangdong Ocean University,Zhanjiang 524088,China)(Received 11 August 2016;revised manuscript received 14 September 2016)

Liao Xiang-Ping et al.(Chin.Phys.B 23 020304,2014)pointed out that the method of weak measurement and quantum weak measurement reversal can protect entanglement and improve the fidelity of three-qubit quantum state.We generalize the method of weak measurement to the case of qudit state in this paper.By using the operation of weak measurement and quantum weak measurement reversal,we investigate the evolution dynamics of fidelity and fidelity improvement for qudit state under amplitude damping decoherence.We compare two kinds of operations:one is to let the input qudit state cross the amplitude damping decoherence directly,and the other one is that we fi rst make a weak measurement operation on the input qudit state,then through the amplitude damping decoherence, fi nally an operation of quantum weak measurement reversal is done with the output qudit state.We discuss the GHZ state,W state,CL state and some special separable states exactly and obtain the analytic expressions of fidelity and fidelity improvement for qudit state before and after the weak measurement and quantum weak measurement reversal operation.According to the analytic expressions we plot the evolution curves against its corresponding parameters.The e ff ects of corresponding parameters are discussed and a susceptible protection region of the qudit state is also given in the context.The results show that the structure of qudit state is the determined factor to the e ff ect of weak measurement and quantum weak measurement reversal.There are some di ff erent e ff ects on the di ff erent structured qudit states.For entangled state,the fidelity of qudit GHZ state can be protected in a relatively big evolution region,most part of the fidelity improvement is in the upper part of the zero reference plane.While the fidelity of qudit W state can be improved e ff ectively in the whole evolution region,which is a perfect protection.The evolution regulations of qudit CL state and Dick state are between evolution regulations of the GHZ state and W state.When we input some special separable qudit states which have similar structures to W state,their fidelity and fidelity improvement are almost the same as W state’s.It is demonstrated that the structure of qudit state is important for the weak measurement in a step.This work is meaningful for the quantum information process.

weak measurement,qudit,amplitude, fidelity

10.7498/aps.66.010301

∗广东省自然科学基金(批准号:2015A030310354)和广东海洋大学优秀青年骨干教师基金资助的课题.

†通信作者.E-mail:940038299@qq.com