基于前冲康普顿电子高能伽马能谱测量系统设计∗

贾清刚 张天奎 许海波

1)(中国工程物理研究院北京应用物理与计算数学研究所,北京 100094)2)(中国工程物理研究院激光聚变研究中心,绵阳 621900)(2016年7月3日收到;2016年8月22日收到修改稿)

基于前冲康普顿电子高能伽马能谱测量系统设计∗

贾清刚1)†张天奎2)许海波1)

1)(中国工程物理研究院北京应用物理与计算数学研究所,北京 100094)2)(中国工程物理研究院激光聚变研究中心,绵阳 621900)(2016年7月3日收到;2016年8月22日收到修改稿)

除中子外,聚变核心同时释放大量高能伽马,其能谱可反映聚变过程的关键物理参数,并为过程诊断提供重要信息.由于聚变伽马的时间与能量特性,需要设计高探测效率及能量分辨率的伽马谱仪.根据高能伽马谱仪的概念设计(gamma-to-electron magnetic spectrometer),针对该系统中伽马-电子转换靶、电子偏转汇聚、电子探测等关键环节进行优化设计以提高系统探测效率及能量分辨率.其中采用Monte-Carlo程序Geant4模拟研究了伽马-电子转换靶中康普顿散射与多次库仑散射对由转换靶出射电子的能谱与角分布的影响.开发并行遗传算法对复杂几何偏转磁场参数进行优化,得到低强度(小于100 Gauss)复杂边界偏转磁场.根据系统优化设计结果,采用Geant4模拟了该系统对不同能量伽马的响应.此外,还可模拟该系统对特征聚变伽马能谱的测量,结果显示,该系统可在聚变中子产额分别为2.5×1015及1.2×1016条件下,对10—20 MeV高能伽马能谱测量实现能量分辨分别满足0.5 MeV(小于5%)及0.25 MeV(小于2.5%),说明该系统可用于聚变过程伽马能谱的诊断.

能谱测量,聚变伽马射线,磁偏转系统,Geant4

1引 言

测量聚变产生的高能伽马能谱对聚变过程的诊断具有重要意义.高能伽马能谱测量主要针对能量介于10—20 MeV的伽马射线,如图1所示,包括由D-T聚变反应直接产生的16.7 MeV,以及2H(n,γ)3H等反应所产生的伽马射线.能谱测量的能量分辨率需要优于5%才能有效区分这些伽马射线.已有的高能X射线能谱测量多采用基于衰减透射的堆栈滤片方法[1,2],然而该方法对高能伽马测量时的能量分辨无法满足需求.Kim等[3,4]提出通过前冲康普顿电子结合偏转磁场以测量高能伽马谱的方法GEMS(gamma-to-electron magnetic spectrometer),并通过理论计算估计该系统可用于聚变过程的伽马诊断.GEMS概念中所涉及的关键物理过程需进行深入研究.在转换靶中,伽马射线与靶材料产生电子,转换效率角度需要厚转换靶.然而,若采用厚靶,所需的高能前冲电子在靶材料中能损将上升,其前冲特性也会因多次库仑散射而丧失,这给后续准直筛选高能电子带来不利影响.此外,不同位置相同能量的前冲电子在磁场中偏转及汇聚也给偏转磁场的设计带来挑战.本文首先采用Monte Carlo程序Geant4对伽马经转换靶产生电子的前冲性(角度分布)、电子能谱及束流强度特性进行模拟研究.采用并行遗传算法结合龙格-库塔方法优化设计出偏转磁场系统,及相应探测布局.使用Geant4对优化后的系统进行建模,模拟结果显示系统优化得到的系统可满足聚变高能伽马谱测量需求.

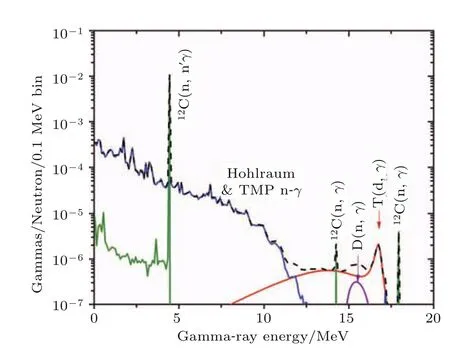
图1 (网刊彩色)聚变伽马能谱[3]Fig.1.(color online)Energy spectrum of laser driven fusion[3].

2转换靶设计

2.1 康普顿散射

转换靶设计主要目的是提升伽马-目标电子的转换效率,该转换效率受以下因素影响:1)康普顿电子角分布;2)电子在靶中多次库仑散射对电子角度-能量相关性的影响.由于康普顿散射中电子结合能远小于伽马射线能量,散射过程可近似为弹性散射,康普顿电子动能Ee与其散射角ω的关系联立(1)式与(2)可得.

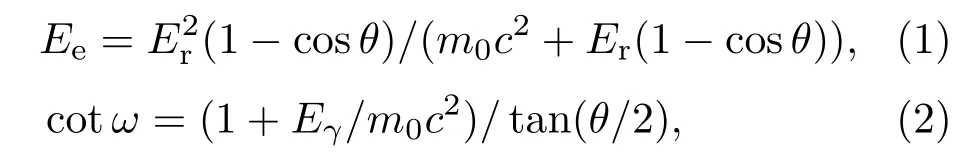
其中Eγ为入射伽马能量,m0c2为电子静止能量,θ为伽马散射角.当入射伽马与电子对心碰撞,并发生反散射时,康普顿电子获得最大能量并沿伽马入射方向输运,此时电子散射角为0.图2所示为计算得到能量介于10—20 MeV的伽马致康普顿电子的能量与散射角关系,其中能量坐标定义为电子能量与最大电子能量的相对偏差.

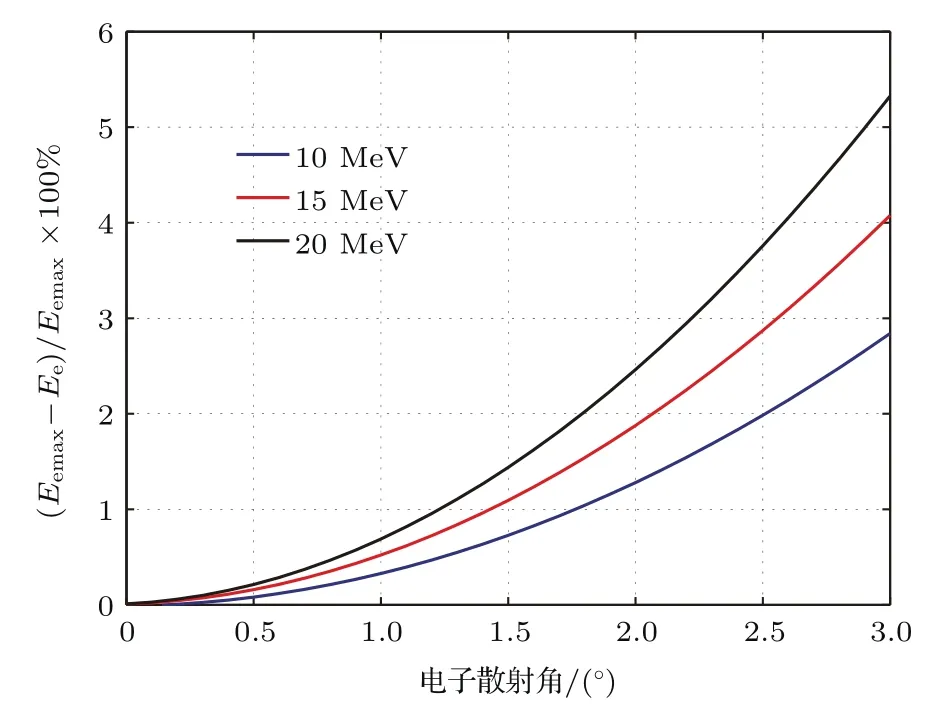
图2 (网刊彩色)康普顿电子能量与散射角Fig.2.(color online)The energy of Compton electron vs scattering angular.

由图2可知,康普顿电子前冲性与电子能量呈正相关,对于10—20 MeV能量电子,当散射角小于3°(约0.05mrad)时,考虑微分截面后电子能量弥散约3%.虽然康普顿电子角度-能量关系及相应截面可采用弹性散射与Klein-Nishina公式描述,但康普顿电子在转换靶中进一步输运时,电子电离能损及多次库仑散射导致的角度与能量弥散均会破坏靶出射电子的能量与角度相关性.

2.2 电离能损及多次库仑散射模型

目前,多次库仑散射普遍采用Moliere模型进行描述,并可通过相关计算获得散射角分布均方根及位移均方根.使用Geant4程序,并采用G4ELivermore-Physics电磁物理模型[5]及截面模拟电子电离能损及电子多次库仑散射.通过模拟电子垂直入射1mm厚铍靶,得到靶后端面出射的电子能量及角度分布如图3和图4所示.

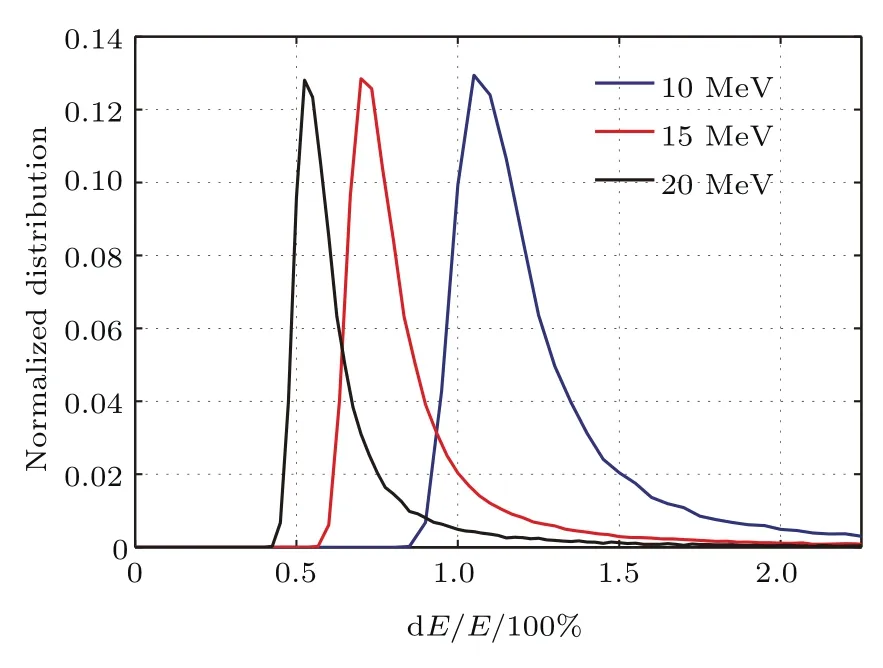
图3 (网刊彩色)电子能损率分布与能量关系图Fig.3.(color online)The functions of election energy on the energy loss in converter.

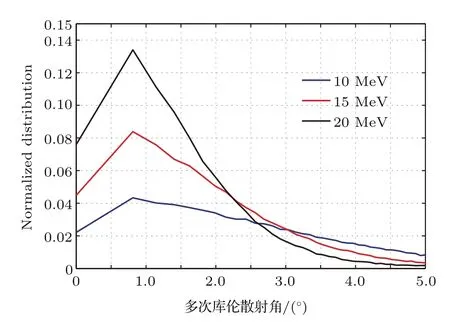
图4 (网刊彩色)多次库仑散射角分布与能量关系Fig.4.(color online)The functions of election energy on the angular distribution induced by multiple Coulomb scatterings.

由图3可知,虽然电子经过1mm厚薄铍靶后,能量损失约1%—2.5%,但电子能量弥散(按半高宽计)均小于0.5%,即电子在薄靶中的电离能损对最终探测器能量分辨带来的影响较小.图4中可见,电子能量越高,多次库仑散射带来的角度弥散越小.多次库仑散射对电子的角度(前冲性)与能谱分布的影响较为复杂,应结合准直一并考虑.主要体现为:高能前冲电子经多次库仑散射可能被准直器阻挡,而较大散射角的低能电子经多次库仑散射后也有可能通过准直系统.

2.3 伽马-电子转换及准直模拟

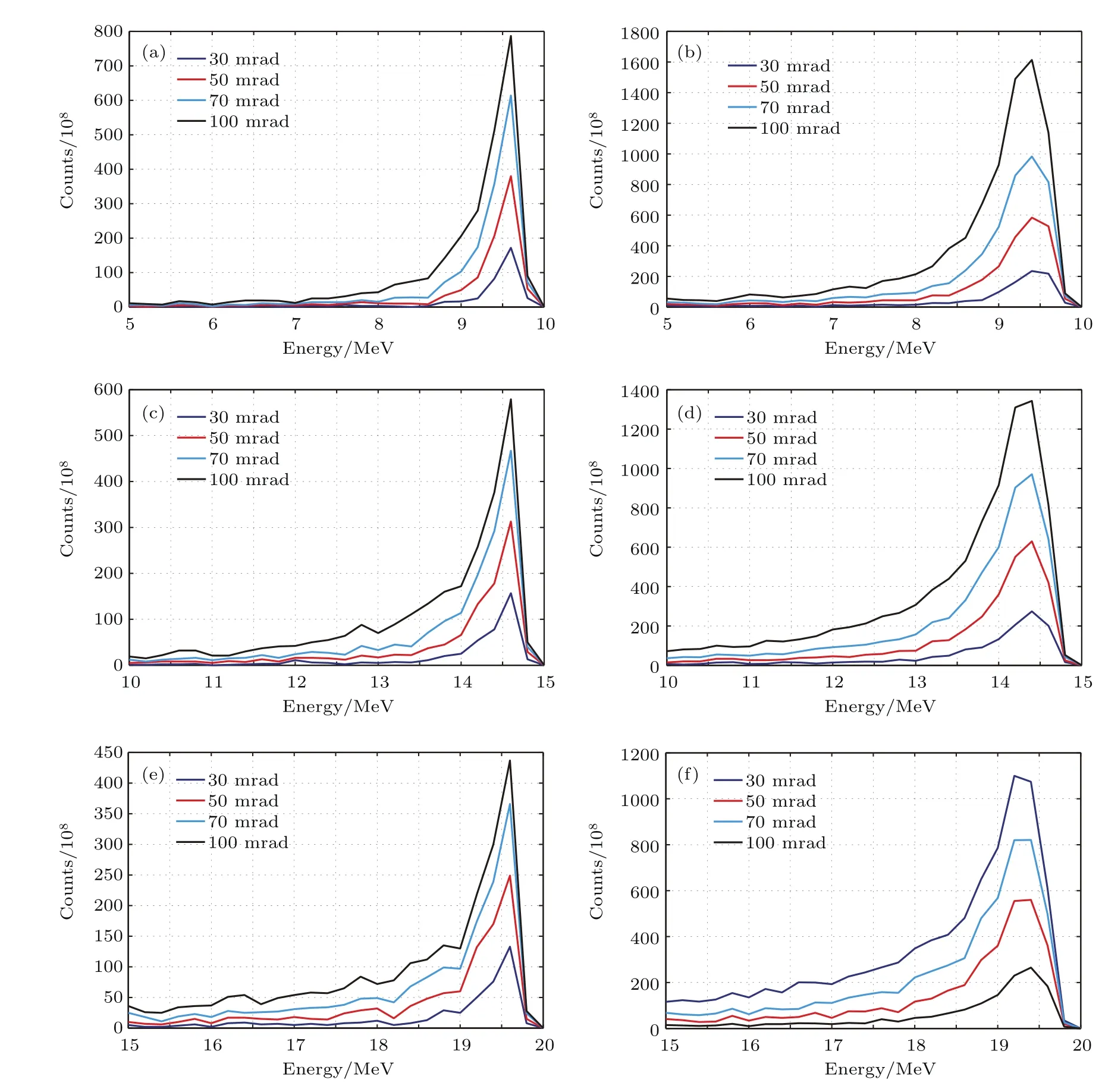
图5 (网刊彩色)伽马能量、靶厚度与准直对出射电子能谱的影响(模拟入射伽马数为108) (a)10 MeV伽马与0.5mm铍靶;(b)10 MeV伽马与2mm铍靶;(c)15 MeV伽马与0.5mm铍靶;(d)15 MeV伽马与2mm铍靶;(e)20 MeV伽马与2mm铍靶;(f)20 MeV伽马与2mm铍靶Fig.5.(color online)The energy distributions of electron with the variance of incident gamma(108used in simulation)energy,the thickness of Be converter and the collimation angular:(a)10 MeV gamma on 0.5mm Be;(b)10 MeV gamma on 2mm Be;(c)15 MeV gamma on 0.5mm Be;(d)15 MeV gamma on 2mm Be;(e)20 MeV gamma on 0.5mm Be;(f)20 MeV gamma on 2mm Be.

伽马-电子转换过程涉及的物理过程较为复杂,影响最终电子能量-角度分布的宏观参数有靶厚度与伽马能量.使用Geant4程序对能量为10—20 MeV伽马入射0.5及2mm铍靶并产生电子的过程进行模拟,得到不同准直角下电子的能谱分布,如图5所示.对比相同能量不同靶厚情况,靶越厚,转换电子的强度越高,但2mm厚靶得到的电子能量展宽也较大,能量分辨(按半高宽计下同)约3%—5%.0.5mm薄靶的能量分辨基本优于3%,但所产生的有效电子强度为2mm靶的25%.当伽马能量及靶厚度固定条件下,准直角越小,理论上获得的电子能谱展宽越小.从模拟结果来看,薄靶及厚靶所获得的电子能谱展宽与准直角的正相关性并不十分明显,但获得电子的强度是随准直角的增大而升高的.此外,随着准直角变小,电子能谱在低能区域延伸的“拖尾”会明显降低,这将有利于解谱工作.靶厚度及准直角均可影响转换效率(获得电子计数)及能量分辨,而这两个指标也是相互矛盾的,应根据实际的伽马强度合理选择能量分辨及靶厚度.例如,当D-T中子产额为1015时,对应16.7 MeV伽马产额约1010,根据文献[4]中给出的相关参数可知,转换靶距聚变源最近距离为2m,磁场厚度为10cm,初步设计出的磁场可接收(可进一步优化提高)电子束流的横向宽度为40cm,即不考虑准直效应及电子束发散角的情况下,靶有效面积为0.04m2,而使用2mm靶及30mrad准直角时,在16.7±0.25 MeV的能量区间内将会有40个目标电子可供探测.若要满足统计偏差降至10%,还需将中子产额提高2.5倍.若中子产额为1016,使用0.5mm厚靶及30mrad准直角,在16.7±0.1 MeV区间内预计可探测到70个目标电子.

3电子轨迹及偏转磁场设计

磁场设计时假设转化靶出射电子为面源平行束,设计出的磁场应将相同能量不同位置入射的电子偏转汇聚到特定探测区域.

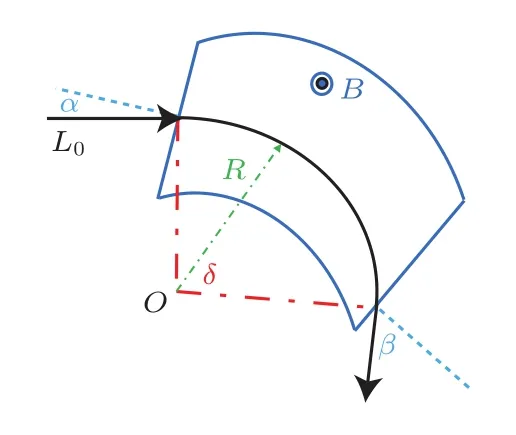
图6 电子在偏转磁场中的轨迹Fig.6.The electron trace in magnet.

如图6所示,设电子能量为Ee(MeV),磁通量密度为B,则电子在该磁场中的偏转曲率半径R可由(3)式计算:

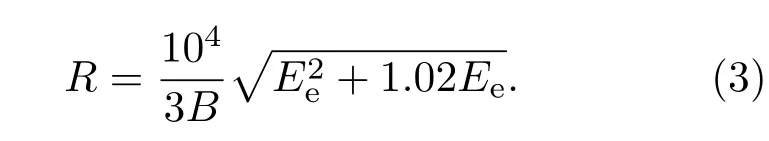
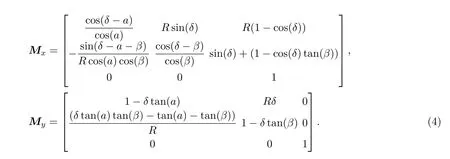
当偏转磁场几何与强度参数确定后,其入射边缘角 α,出射边缘角 β,偏转角δ,参考轨道半径R均可通过计算获得.则电子在该带有边缘角的满足“硬边界”近似磁偏转系统中的传输矩阵为这里需要说明的是,磁场分布满足“硬边界”近似,即磁场强度均一且边缘强度呈阶跃式变化.若磁场尺寸较小且磁间距较大时,还需要考虑边缘效应的影响,可根据实际情况采用等效方法或修正对(4)式进行改进,详细参见文献[6].

若采用电子平行入射假设,可将入射电子参数化简为单一值L0(代表该入射电子与参考位置的纵向水平距离),对于相同能量的电子,当参数L0变为L1乃至Ln时,形成n条电子轨迹,若这些轨迹最终汇聚或相互交点位置聚集在较小范围内(探测区域),磁场对不同位置相同能量电子的汇聚可满足要求.此外,对于不同能量的电子,其汇聚点或聚集范围不应重叠且间距较大,这样才能保证较高的能量分辨率.

由于磁偏转系统参数较多,参数间相互耦合,这里采用主仆式并行遗传算法[7]对系统进行优化设计.图7为该算法的流程图,算法一次可计算n个个体的适应度函数,每个个体适应度函数包含F1与F2,分别用于计算相同能量电子汇聚位置范围及不同能量电子汇聚范围的距离,二者共同决定系统的能量分辨率.

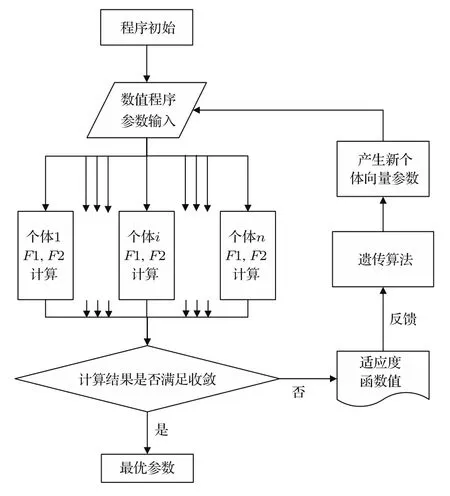
图7 并行遗传算法流程图Fig.7.Flow of slave-master parallel genetic algorithm.

仅追求高能量分辨率时,经遗传算法设计出的磁场及电子轨迹如图8所示,其中磁场强度为50 Gauss,图中相同颜色轨迹的电子能量分别为注释能量及注释能量值的95%.

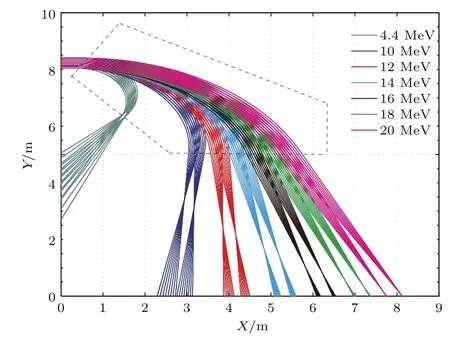
图8 (网刊彩色)磁场对能量偏差为5%电子汇聚Fig.8.(color online)Traces of electrons with various energy in magnet(energy resolution 5%).

图8中优化后磁场对10—20 MeV平行束电子的理论能量分辨优于1%,然而该磁场尺寸较大约为4m×8m,系统总重量可能超过实际可行范围.因此,将磁场尺寸作为约束条件纳入遗传算法优化算法中,优化得到强度约300 Gauss的紧凑型磁场,其尺寸约2m×4m,如图9所示.对比图8与图9中的电子轨迹可知,紧凑型磁场对低能4.4 MeV电子的能量分辨率只有约5%,不及图8所示磁场的能量分辨率,但该系统仍可满足实验对能量分辨率的要求.

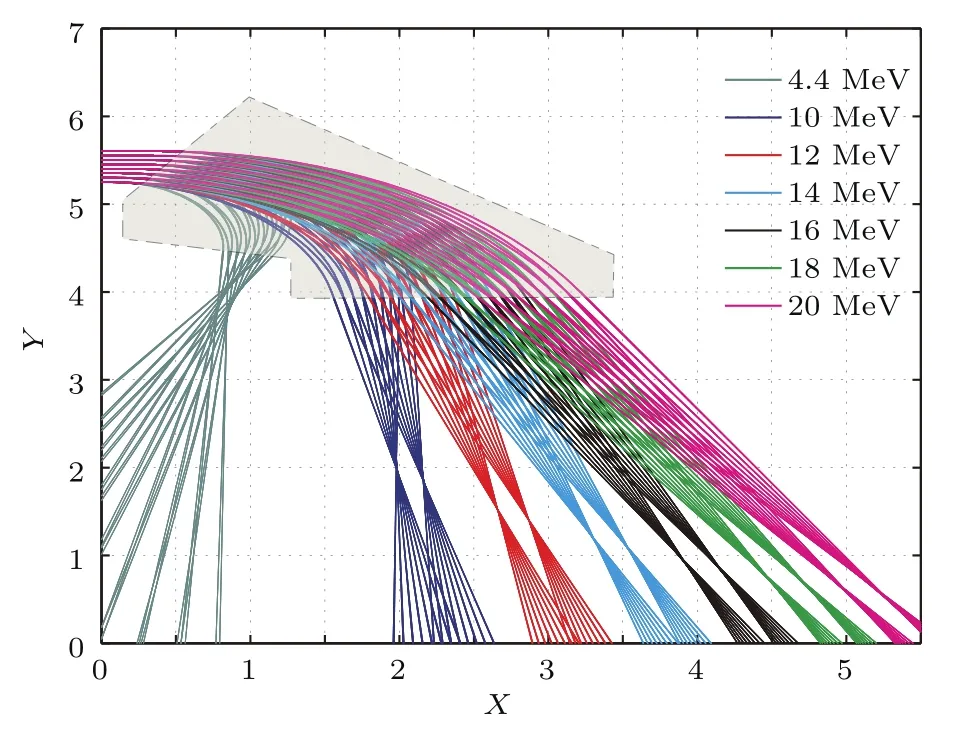
图9 (网刊彩色)紧凑磁场对能量偏差为5%电子汇聚Fig.9.(color online)Traces of electrons with various energy(resolution 5%)in compact magnet.

数值计算表明,不同能量电子的汇聚点并非如文献[4]中所述在同一平面上.探测器位置摆放不当将会对能量分辨率带来不利影响.经数值方法计算得到的探测区域的位置分布满足二次曲线(最小二乘拟合),最终系统的Geant4可视化模拟如图10所示.其中需要说明的是,Geant4使用龙格-库塔方法直接获得电子进出磁场时的位置及角度信息,电子在磁场中可视化轨迹为直线,并不影响模拟结果的正确性.

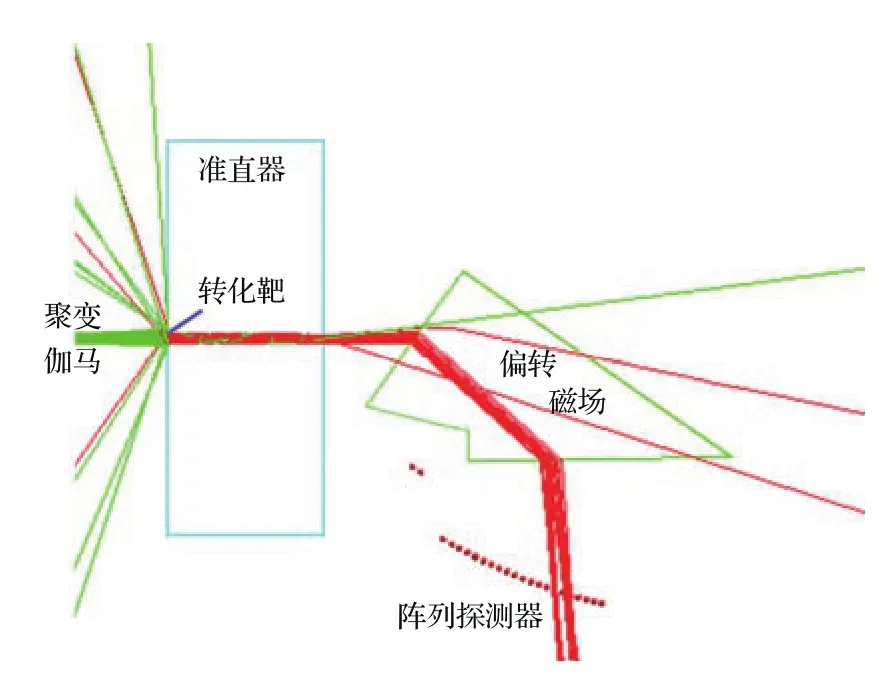
图10 (网刊彩色)伽马能谱测量系统Geant4可视化Fig.10.(color online)Visualision of gamma spectrum measurement given by Geant4.

4探测系统的响应

使用Geant4模拟探测器组对不同能量伽马的响应进行模拟(转换靶距聚变点源2m),认为探测器对电子的探测效率为100%,结果如图11所示.对于相同能量伽马而言,具有2mm靶系统的灵敏度为0.2mm靶系统的2至5倍,并且探测器响应基本不随伽马能量升高而降低,可见由于多次库仑散射及准直等因素,最终探测到的前冲电子数目并非与靶厚度及康普顿电子产额呈正比.薄靶系统对伽马的灵敏度随伽马射线能量升高而降低,正体现了伽马与材料反应截面变化特点,说明薄靶产生的康普顿电子的前冲性与能量有较大的相关性.从能量分辨角出发,0.2mm薄靶系统的能量分辨按半高宽计约为0.25 MeV,为2mm厚靶约0.7 MeV的35%.此外,厚靶系统对伽马的响应函数除了主峰外,拖尾现象也较为严重,因此高能段信息会对低能段信息产生一定影响.拖尾现象可解释为:高能伽马产生的部分次级低能电子经准直后进入磁场(小概率),由于其旋转半径较小,会对针对能量较低电子的探测器(探测器位置靠左,见图10)带来干扰.

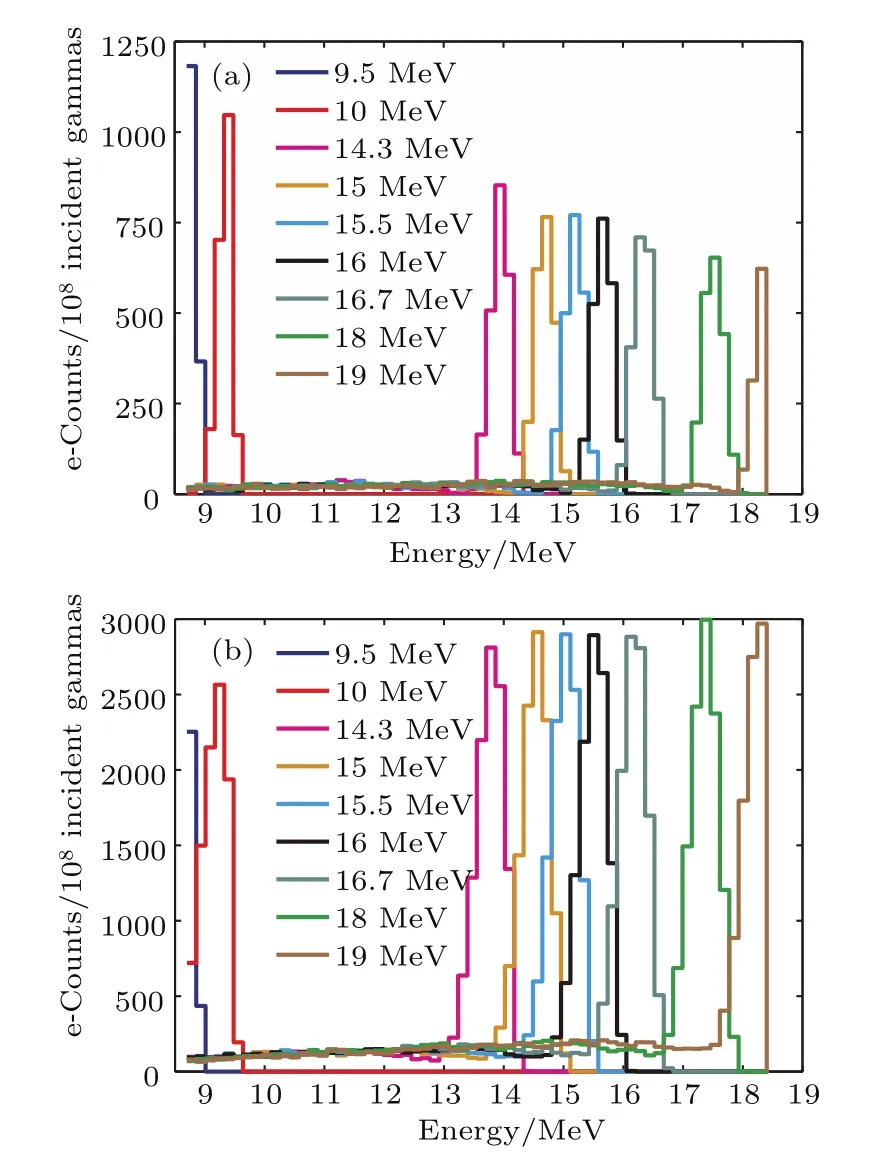
图11 (网刊彩色)铍靶厚为0.2mm(a)及2mm(b)时系统对不同能量伽马的响应Fig.11.(color online)Responses of gammas with di ff erent energy when 0.2mm(a)and 2mm(b)thick Be converter is used.

根据图1所示伽马能谱,设目标10—19 MeV能段的伽马能谱如图12所示,使用Geant4模拟0.2mm靶系统及2mm靶系统对该能谱伽马的探测,得到的系统响应如图13所示.相比2mm靶系统,由0.2mm靶系统的响应函数可较好地甄别原始谱所含4个特征伽马峰,但0.2mm靶系统需要的中子产额较高.若要通过响应函数获得更精确的聚变伽马能谱分布,还需采用合适算法进一步解谱,相关线性及非线性拟卷积解谱算法较多,将于其他文章中进行深入讨论.

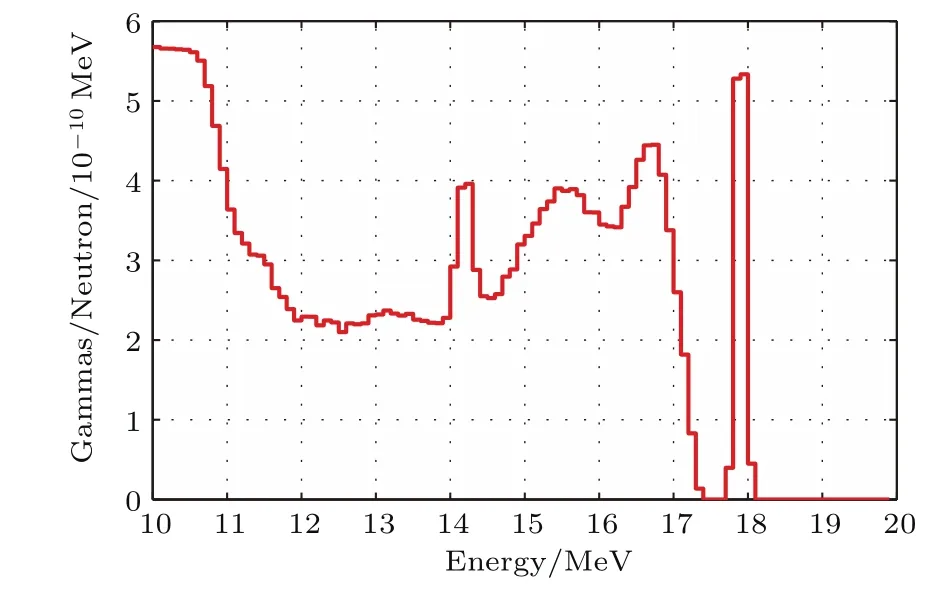
图12 模拟使用的聚变伽马谱Fig.12.Assumed gamma spectrum in the simulation.

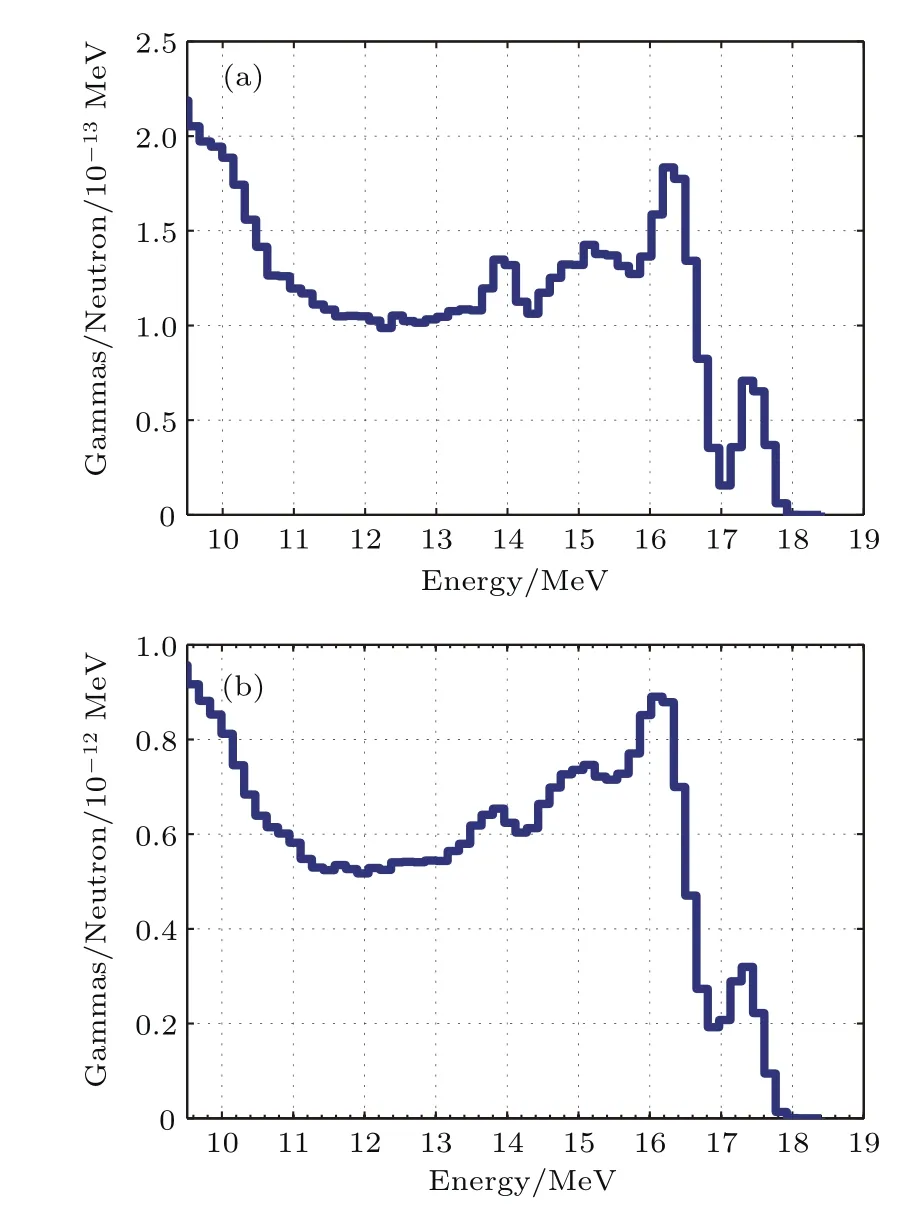
图13 铍靶厚为0.2mm(a)及2mm(b)时系统对聚变伽马的响应(采用聚变中子产额归一包含空间探测效率)Fig.13.Detector response when 0.2mm(a)and 2mm(b)thick Be converter is used(normalized to one fusion neutron).

5讨论与结论

通过对伽马-康普顿电子转换物理环节的理论及模拟研究,分析了康普顿散射与多次库仑散射对电子前冲角分布与能量分布相关性的影响,采用Geant4数值模拟了伽马能量、转换铍靶厚度与准直角对所产生康普顿电子的影响.研究康普顿电子在磁场中的偏转及汇聚,将数值模拟算法与遗传算法相结合,优化设计出具有较高能量分辨率的偏转磁场,模拟研究表明,根据聚变产额优选靶,可使系统在产额为2.5×1015及1.2×1016条件下实现能量分辨分别为0.5 MeV(小于5%)及0.25 MeV(小于2.5%).由于系统对伽马的响应可能随能量变化,伽马能谱的精细反演,并非简单逆卷积问题,值得进一步研究.

[1]Wang Y,Li Q,Li T T 2013 High Power Laser Part.Beams 25 3017(in Chinese)[王毅,李勤,李天涛 2013强激光与粒子束25 3017]

[2]Su Z F,Yang H L,Qiu A C,Sun J F,Cong P T,Wang L P,Lei T S,Han J J 2010 Acta Phys.Sin.59 7729(in Chinese)[苏兆锋,杨海亮,邱爱慈,孙剑锋,丛培天,王亮平,雷天时,韩娟娟2010物理学报59 7729]

[3]Kim Y,Herrmann H W,Hilsabeck T J,Moy K,Stoeffl W,Mack J M,Young C S,Wu W,Barlow D B,Schillig J B,Sims J R,Lopez F E,Mares D,Oertel J A,Hayes-Sterbenz A C 2012 Rev.Sci.Ins.83 10D311

[4]Kim Y,Herrmann H W,Jorgenson H J,Barlow D B,Young C S,StoefflW,Casey D,Clancy T,Lopez F E,Oertel J A 2014 Rev.Sci.Ins.85 11E122

[5]Buis E J,Vacanti G 2009 Nucl.Instrum.Methods Phys.Res.Sect.A 599 260

[6]Liu J Q 2004 The Optics of Charged Particle Beams(Beijing:Higher Education Press)pp126–171(in Chinese)[吕建钦 2004带电粒子束光学(北京:高等教育出版社)第126—171页]

[7]Wang X P,Cao L M 2002 The Genetic Algorithm-Theory,Application&Implementation (Xi’an:Xi’an Jiaotong University Press)pp79–85(in Chinese)[王小平,曹立明 2002遗传算法——理论、应用与软件实现 (西安:西安交通大学出版社)第79—85页]

PACS:07.77.Ka,29.40.–n,29.30.KvDOI:10.7498/aps.66.010703

*Project supported by the Postdoctoral Science Foundation of China(Grant No.2015M581028),the National Natural Science Foundation of China(Grant Nos.11675021,11505166),and the Science and Technology Developing Foundation of China Academy of Engineering Physics(Grant No.2014A0402016).

†Corresponding author.E-mail:QGJIA_XJTU@126.com

Optimization design of a Gamma-to-electron spectrometer for high energy gammas induced by fusion∗

Jia Qing-Gang1)†Zhang Tian-Kui2)Xu Hai-Bo1)

1)(Institute of Applied Physics and Computational Mathematics,Beijing 100094,China)2)(Science and Technology on Plasma Physics Laboratory,Laser Fusion Research Center,China Academy of Engineering Physics,Mianyang 621900,China)(Received 3 July 2016;revised manuscript received 22 August 2016)

Apart from neutrons,the fusion core produces gamma rays during fusion reaction.The spectrum of gamma ray can provide very important information for fusion diagnosis.However,due to the gamma energy and yield in one fusion pulse being both lower,the gamma spectrometer used should have high detection efficiency and energy resolution.The concept of a Gamma-to-electron magnetic spectrometer(GEMS)provides the idea to build up such a spectrometer to meet this requirement.Based on this concept design,four important parts of this facility are investigated.The fi rst part is the gamma-electron converter.The main physics processes include Compton scattering of gamma ray with converter material generating electron,the electron multiple Coulomb scattering(MCS)inside the converter and the electron attenuation.A ff ected by the thickness of convector,these processes give a complex in fl uence on the detection efficiency and angular-energy distribution of the electrons which are emitted from the downstream face of the convector.The Monte Carlo code Geant4is employed to investigate thee ff ects of Compton scattering,MCS and converter thick on the angular-energy distribution.The second one is the collimation.The collimation is used to select the forward direction,the performances of cuto ffangle of the collimator on the detection efficiency and resolutions,the correlation between electron transportation direction and energy,are also studied using Geant4code.The third part is the dipole magnetic field.There are several geometric and magnetic parameters,therefore,a multi-thread parallelized genetic algorithm is developed to obtain the best result.Both the irregular geometric shape and dipole magnetic fi eld strength are optimized to achieve the best energy resolution and detection efficiency.The obtained magnetic fi eld has an intensity of less than 100 Gauss,and its performance on gathering elections is also veri fi ed by Geant4code.The last one is the location of electron detectors.The study shows that all the electron detectors should be located not in a straight line but a quadratic curve.Then the optimized spectrometer is simulated by Geant4to obtain the responses of gamma rays with various energies.For the gammas provided by fusion reaction,the simulation shows that when the neutron yields are about 2.5×1015and 1.2×1016,the energy resolutions reach 0.5 MeV and 0.25 MeV,respectively,provided that di ff erent thick Be converters are employed.All in all,this optimized GEMS can be employed to measure the spectrum of gamma rays generated fom the fusion reaction.

spectrometer,fusion gamma ray,dipole,Geant4

10.7498/aps.66.010703

∗中国博士后科学基金(批准号:2015M581028)、国家自然基金(批准号:11675021,11505166)和中国工程物理研究院科学技术发展基金(批准号:2014A0402016)资助的课题.

†通信作者.E-mail:QGJIA_XJTU@126.com