纵波光学声子耦合对级联型电磁感应透明半导体量子阱中暗-亮光孤子类型的调控∗
2017-07-31唐宏王登龙张蔚曦丁建文肖思国
唐宏王登龙†张蔚曦丁建文肖思国
1)(湘潭大学物理与光电工程学院,湘潭 411105)2)(铜仁学院物理与电子工程学院,铜仁 554300)(2016年4月19日收到;2016年10月3日收到修改稿)
纵波光学声子耦合对级联型电磁感应透明半导体量子阱中暗-亮光孤子类型的调控∗
唐宏1)王登龙1)†张蔚曦2)丁建文1)肖思国1)
1)(湘潭大学物理与光电工程学院,湘潭 411105)2)(铜仁学院物理与电子工程学院,铜仁 554300)(2016年4月19日收到;2016年10月3日收到修改稿)
利用多重尺度法,解析地研究了计及纵波光学声子耦合弛豫效应下级联型三能级电磁诱导透明半导体量子阱介质中时间光孤子的动力学特征.结果表明:纵波光学声子耦合强度的大小能有效调控体系时间光孤子的类型;发现孤子的群速度也可通过纵波光学声子耦合强度和控制光来调控.这为实验上如何操控半导体量子阱的孤子动力学提供了一定的理论依据.
纵波光学声子耦合,电磁诱导透明,半导体量子阱
1 引 言
通过电磁诱导透明(EIT)技术[1,2],光学介质能获得显著的非线性效应且极大地抑制了介质对入射光的吸收[3−5].通常人们把利用电场诱导透明技术应用的光学介质称为EIT介质.最早EIT介质的应用是在超冷原子体系,早在二十世纪九十年代就受到关注[6−9].最具代表意义的是Hau等[9]在超冷钠原子介质中把光脉冲的群速度降到了17m/s,由于光的超慢传输便以将其存储起来.因此,EIT介质中光孤子超慢传输[9−14]和光存储[15]一直是非线性光学研究的热点之一.然而,由于超冷原子介质温度过低,材料性能难以精准控制,很难形成大规模处理,因而在实际应用中受到很大制约.随着半导体工艺的发展,半导体量子阱、量子点、量子线等半导体量子局限材料被认为是最有希望实现EIT应用的介质.这是因为这类材料不仅具有分立的能级结构,而且还拥有很大的非线性光学参数、电偶极矩、参数可调及灵活性很强等[16−18]性质.
作为半导体量子结构局限材料之一的半导体量子阱,其导带能级之间的纵波光学声子交叉耦合效应已被实验证实[19−22].研究表明,纵波光学声子交叉耦合效应能调节N型四能级非对称半导体量子阱中的光孤子的幅度和群速度[23];且当考虑高阶效应时,纵波光学声子交叉耦合效应对N型四能级非对称半导体量子阱的孤子动力学具有一定的影响[24].然而,迄今为止很少研究级联型量子阱中纵波光学声子耦合效应对孤子动力学性质的影响.
近年来的研究表明,暗孤子在传输上较亮孤子有明显的优势.例如在相同的介质中,传输相同的距离,暗孤子的脉冲幅度衰减比亮孤子慢,暗孤子的脉冲展宽也比亮孤子慢.此外,在相同的噪声背景中,暗孤子受到噪声的影响比亮孤子要小[25].因此,怎样实现由亮孤子向暗孤子类型的转化是一个很有意义的研究课题.尽管已有研究表明,在半导体量子阱中,可以通过改变子带间偶极矩跃迁的强度,实现亮孤子和暗孤子之间的相互转换[26];在半导体量子点中,通过改变控制光强度的大小可实现亮孤子和暗孤子之间的相互转化[27].然而一直未展开纵波光学声子交叉耦合效应能否实现对量子阱中亮孤子和暗孤子的转化研究.
半导体量子阱中的暗孤子不仅保持了光孤子在EIT介质中超慢传输便于存储的特点,还能充分利用暗孤子在信息传输上的优势提高半导体材料实际应用的潜力.因此,很有必要研究在量子结构材料中如何实现由亮孤子向暗孤子的转化.
因此,本文重点考虑级联型三能级量子阱中纵波光学声子耦合效应对亮孤子和暗孤子类型的调节作用.研究结果表明:当纵波光学声子交叉耦合强度较小时,能在级联型三能级量子阱中得到稳定的暗孤子;而当纵波光学声子耦合强度较大时,能在级联型三能级量子阱中得到稳定的亮孤子;通过改变纵波光学声子耦合强度的大小还能实现孤子群速度正-负之间的相互转化.
2 级联型三能级半导体量子阱中光孤子的解析解
目前,实验上[28]已能在GaAs/AlInAs多量子阱中利用反Stark分裂效应使半导体量子阱体系能级分裂为键态和反键态,从而形成级联型三能级EIT多量子阱模型,且其能级之间会出现量子相干效应.基于此,我们考虑了一个级联型三能级量子阱,它是由4.8 nm的In0.47Ga0.53As,0.2 nm的Al0.48In0.52As以及4.8 nm的 In0.47Ga0.53As耦合形成的量子阱,相邻的耦合量子阱之间由36 nm厚的调制掺杂Al0.48In0.52As的势垒隔开,共30层[28];以及纵波光学声子弛豫交叉耦合过程,如图1所示.图中的能级|1〉表示粒子布局的初始态,能级|2〉,|3〉分别为反Stark分裂后所形成的键态和反键态.其中探测光Ωp作用在能级|1〉和|2〉之间;控制光Ωc作用在能级|2〉和|3〉之间;κ表示|2〉,|3〉能级之间经过反Stark分裂效应使体系能级分裂为键态和反键态能级之后形成的纵波光学声子弛豫交叉耦合的过程.在相互作用表象下,采用旋波近似和电偶极近似后,级联型三能级EIT多量子阱的哈密顿量为

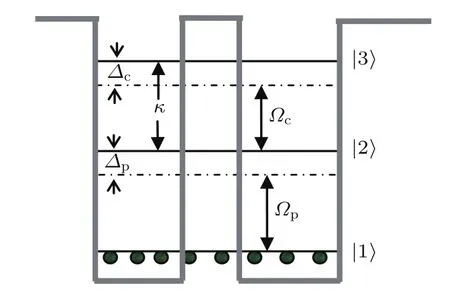
图1 级联型三能级多量子阱模型Fig.1.The model of a mu ltiple cascade-type th reelevel semiconductor quantumwell.
其中Ωp=u21Ep/2ħ和Ωc=u32Ec/2ħ分别表示探测光和控制光的半拉比频率;∆p=ω21−ωp与∆c=ω32−ωc分别为探测光和控制光与相应能级的单光子失谐.ωp和 ωc分别为探测和控制光的中心频率.uij=uij.eL(i,j=1,2,3)表示在能级的电偶极矩.系统的电场矢量其中el,kl及εl分别是极化方向、波矢及第l个场所形成的包络;E.c.表示电场的复共轭项.(1)式中的h.c.代表体系哈密顿量的复共轭项.运用线性薛定谔方程iħ∂Ψ/∂t=HintΨ,就可得到相互作用表象中的麦克斯韦-薛定谔方程组:
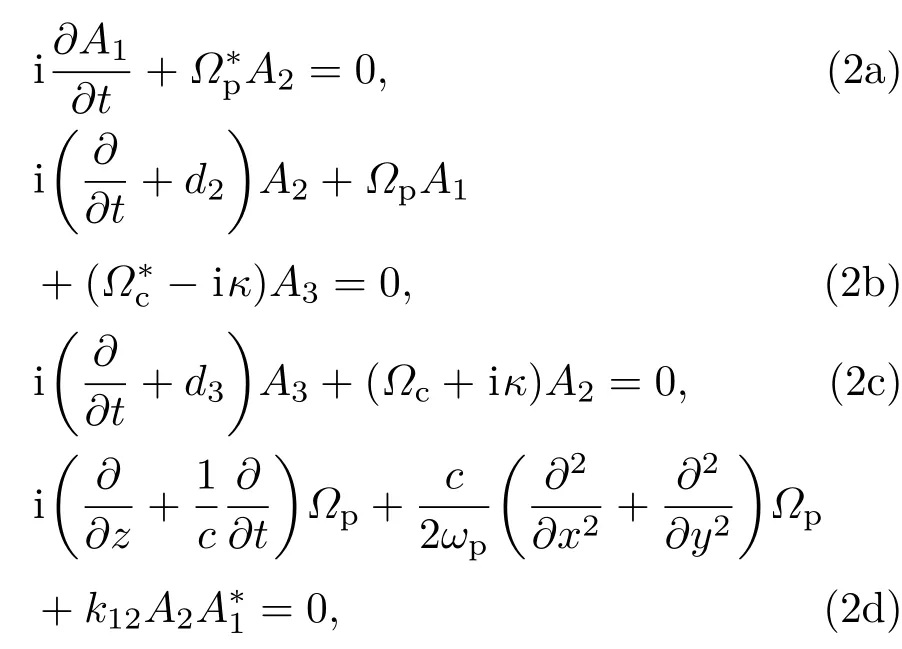
式中d2= −∆p+iγ2,d3= −(∆p+ ∆c)+iγ3.能级|j〉中粒子布局概率幅Aj满足于归一化条件能级|j〉(j=2,3)总的衰减率γj由粒子数衰减γjl(主要受纵波光学声子低温辐射的影响)和相移衰减率γjd(受电子-电子散射、声子散射、弹性截面的粗糙程度的影响)组成,即γj= γjl+ γjd. κ =(γ2lγ3l)1/2描述了|2〉和|3〉能级之间纵波光学声子弛豫的强度,其大小与介质体系温度和相移衰减有关[19−21].方程(2d)的第二项描述的是系统的衍射效应.k12=2πNa|u12|2ωp/ħc是传播系数,其中Na表示原子数密度.
由于方程(2)不可积,一般无法直接得到其解析解.因此我们在此采用多重尺度法[29−32]来研究探测场的演变并对概率幅和探测光做渐近展开,


在一阶的情况下,可得到体系的线性色散关系式为

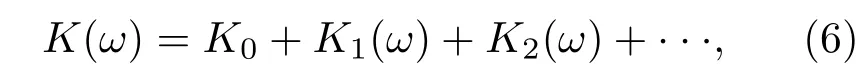
其中K0=ϕ+iα/2,ϕ是通过介质后的单位相移量,α为探测光的线性吸收系数.

K1与探测场的群速度有关,K2描述的是探测场的群速度色散效应.
由二阶可解条件可得
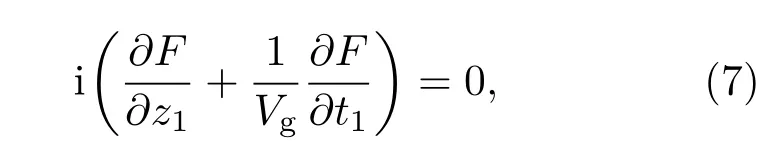
其中Vg=Re(1/K1)是探测光场包络F的传播群速度.
类似地,通过三阶可解条件有

由方程(7)和(8)可得
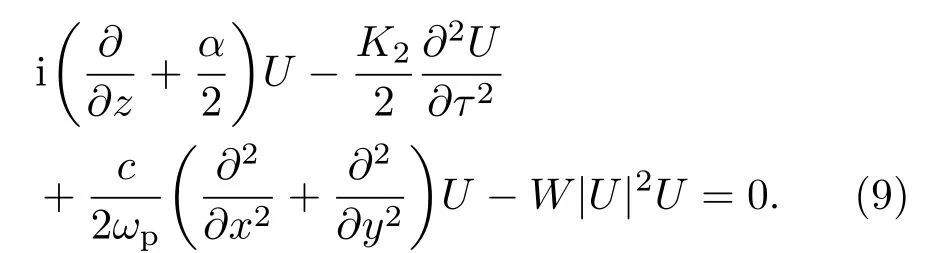

方程(10)中字母下标r表示仅取K2和W的实部.当Wr<0引入无量纲变量z=2LDs,而Wr>0引入z= −2LDs,其他无量纲变量为τ= τ0σ,(x,y)=R⊥(x′,y′),U=U0u. 此外, 引入无量纲参数 d0=2LD/L0,ddiff=2LD/Ldiff,其中是特征色散长度,L0=2/α为探测光有效传输的吸收距离,是衍射距离.假设LD=LNL(LNL是特征非线性效应的长度)就意味着色散效应和非线性效应相平衡形成时间光孤子.
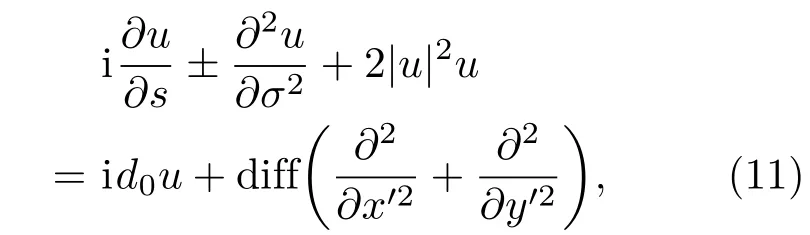
如果L0和Ldiff远远大于LD,在传播距离小于LD内有d0≪0,ddiff≪0[23,27],然后分两种情况讨论.
如果K2rWr<0那么方程(11)可化成非线性薛定谔(NLS)方程,
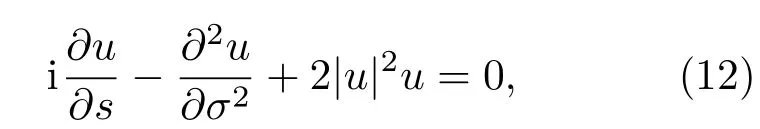
其孤子解为[27]
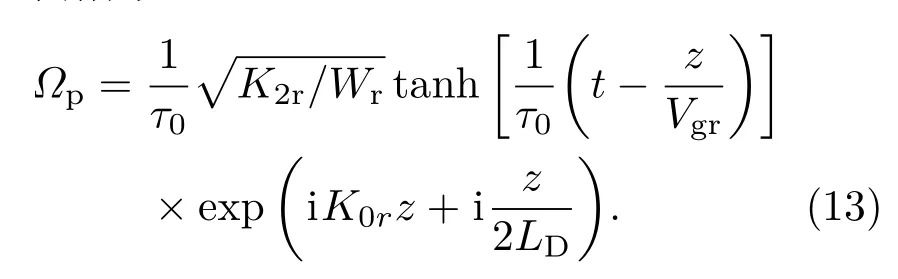
为了检验孤子的稳定情况,基于现有的实验条件[22,31,33],我们可选取实验参数为τ0=10−12s,∆p=0 meV,∆c=0.3×1012s−1,Ωc=5 meV,γ2d= γ3d=0 meV,ω =0,k12=1.0 × 1017s−1,c=3.0×1010cm/s和κ =0.3×1012s−1.随后以方程(13)为初始条件数值计算原始方程,给出不同时刻探测光强度随距离的传播情况,结果如图2所示.从图2可以看出,当t=1.0τ0(图2中实线)时,发现光强度曲线向下凹,且最小值为零,这说明系统中形成了暗孤子.随着时间的推移,当t=3.0τ0(如图2中虚线)及t=5.0τ0(如图2中点线)时,暗孤子向左平移,同时孤子中心处稍稍增大,但波形整体稳定不变.这说明暗孤子可以在系统中稳定地传播.
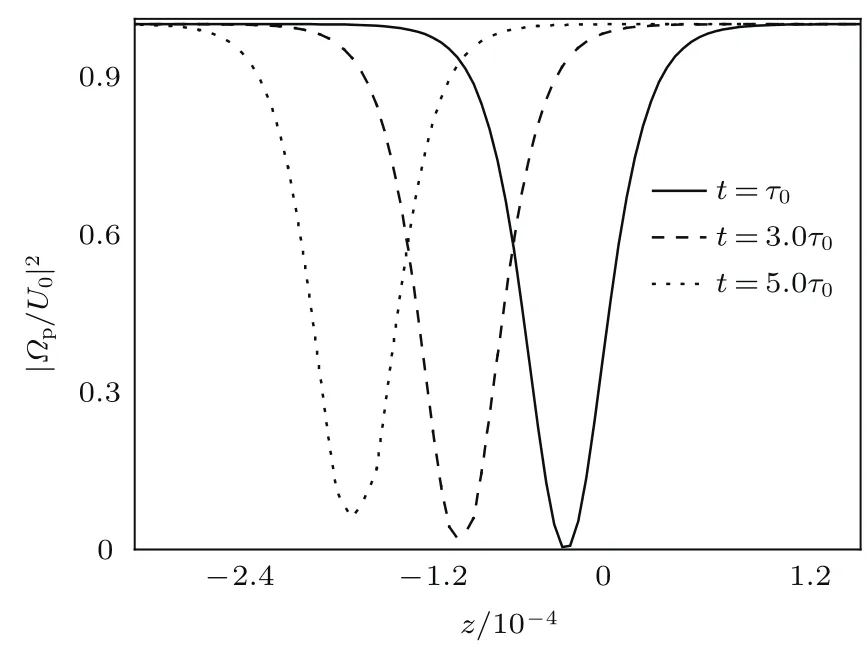
图2 暗孤子的稳定性分析Fig.2.The stability analysis of dark soliton.
如果K2rWr>0,那么方程(11)可以化成NLS方程,
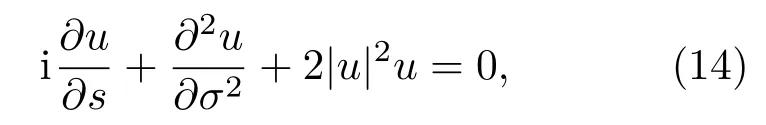
其孤子解是[27]
防洪作用突出。将黄河下游的防洪标准从不足60年一遇提高到1000年一遇,为黄河下游防洪安全提供了保障。2013年,黄河下游已连续14年实现安全度汛。
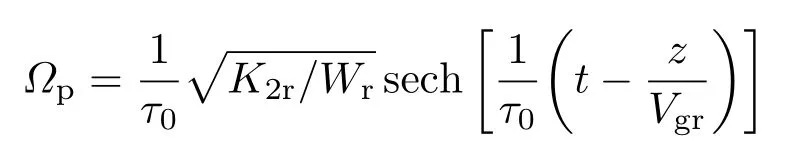

方程(15)描述的是一个以Vgr为速度传播的亮孤子.为了检验该亮孤子的稳定情况,我们仅改变纵波光学声子交叉耦合强度的大小,而其他参数与图2选定的参数的取值完全相同,并给出了不同时刻探测光强度随距离的传播情况,如图3所示.图3所示为以孤子解(15)为初始条件,数值模拟方程(2)的结果(实线、划线及点线分别表示演化时间为t=1.0τ0,t=3.0τ0及t=5.0τ0). 可以看出,当孤子演化时间t=1.0τ0时,光场强度随距离演化存在峰值,且曲线具有高度的对称性,这就是亮孤子.同样地,随着时间的演化,t=3.0τ0及t=5.0τ0时,可以看见亮孤子主体仍然能稳定地向左传播,虽然主波的前沿辐射出小振幅色散波,且孤子幅度有一定的降低,这是由系统的高阶色散贡献的.我们在本文中没有考虑高阶效应.因此,图3说明亮孤子也能在体系中稳定传播.
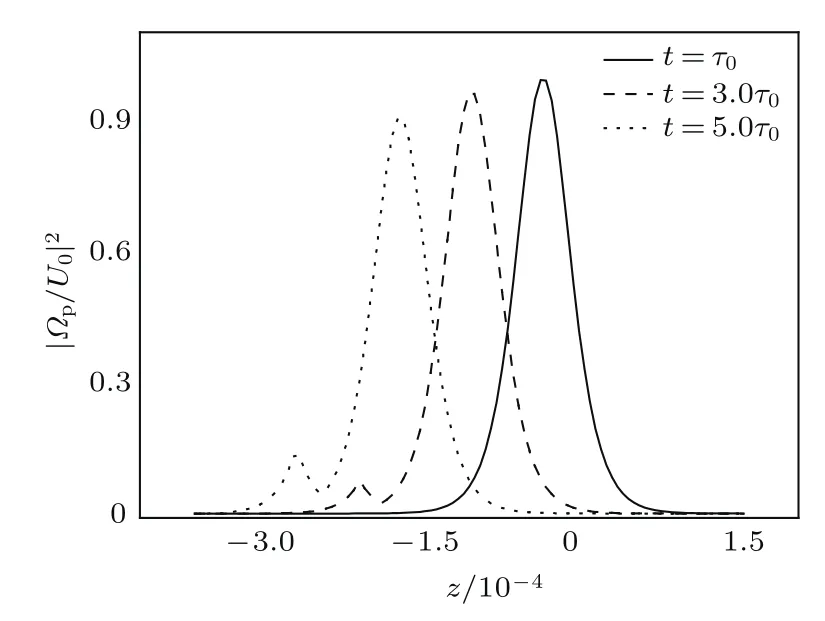
图3 亮孤子的稳定性分析Fig.3.The stability analysis of b right soliton.
3 纵波光学声子耦合强度对体系孤子类型的影响
如前所述,当K2rWr<0时体系中存在稳定传播的是暗孤子,而当K2rWr>0时亮孤子能在体系中稳定地传播.图4给出了群速度色散效应和非线性效应系数实部的乘积(K2rWr)随纵波光学声子耦合强度系数κ的变化,图中所选其他参数与图2一致.
从图4可以看出,群速度色散效应和非线性效应系数实部的乘积(K2rWr)随纵波光学声子耦合强度系数κ的增加而增加.并且,纵波光学声子耦合强度大小范围在0≤κ<0.5×1012s−1时,有K2rWr<0,则体系会产生暗孤子;而当纵波光学声子耦合强度大小范围为0.5×1012s−1< κ ≤ 1.0× 1012s−1时,有K2rWr> 0则体系会产生亮孤子.因此,纵波光学声子耦合强度的大小将能直接决定在体系中所形成的暗孤子或亮孤子类型.这可以解释为纵波光学声子可通过辅助跃迁效应引起能级粒子布局的改变并影响体系内的量子相干与干涉效应,进而改变探测光在介质中的正常色散和反常色散关系,实现孤子暗-亮类型的有效调控.

图4 群速度色散效应和非线性效应系数实部的乘积随纵波光学声子耦合强度的变化Fig.4.The variation of the product of real parts of the coeffi cients of groupvelocity d ispersion and non linear eff ects with the strength of the relaxation of longitud inal optical phonons.
4 纵波光学声子耦合强度对体系孤子群速度的影响
如前所述,通过改变系统纵波光学声子耦合强度,可实现孤子暗-亮类型的有效调控.而EIT介质中的光孤子往往可以实现群速度的超慢传输,为了探究考虑纵波光学声子耦合效应之后光孤子是否仍然具有超慢群速度以及纵波光学声子耦合强度能否对群速度起调控作用,我们数值计算了在不同控制光强情况下孤子群速度与真空中光速的比值随纵波光学声子耦合系数的变化,结果如图5所示(参数均与图4相同).
由图5可知,控制光强度Ωc=3.5 meV(图5中实线),而纵波光学声子耦合强度在0≤κ≤0.35×1012s−1及0.6≤ κ ≤ 1.5×1012s−1时,群速度的大小仅是真空中光速的约万分之二(如插图中的纵波光学声子耦合强度在0≤κ≤0.2×1012s−1时的孤子群速度大小,从插图中实线可以看出群速度大约为−0.0002c).纵波光学声子耦合强度在区间0.35×1012s−1< κ < 0.6×1012s−1内,即区间宽度为0.25×1012s−1时,对孤子群速度存在较为明显的调节效果,尤其是在κ≈0.4×1012s−1时群速度大约可由−0.015c变为+0.015c.随后,增大控制光强度到Ωc=4.5 meV(图5中划线),当0≤κ≤0.45×1012s−1及0.8≤ κ ≤ 1.5×1012s−1时群速度约为0.0004c(插图中划线).当纵波光学声子耦合强度在区间0.45×1012s−1<κ<0.8×1012s−1内对孤子群速度存在较为明显的调节效果,特别是当κ≈ 0.6×1012s−1时群速度大约由−0.035c变为+0.035c.继续增大控制光强度到Ωc=5.5meV(图5中点线),在纵波光学声子耦合强度为0≤κ ≤ 0.55×1012s−1及1.0≤ κ ≤ 1.5×1012s−1时孤子具有约为0.0005c的超慢群速度(插图中点线).当0.55×1012s−1< κ < 1.0×1012s−1时(区间宽度为0.45×1012s−1),纵波光学声子耦合效应对孤子群速度存在较为明显的调节效果,特别是当κ≈ 0.8×1012s−1时群速度大致可调范围从−0.075c变为+0.075c.最后取较大控制光强度Ωc=6.5 meV(图5点划线),0≤ κ ≤0.45×1012s−1及1.3≤ κ ≤ 1.5×1012s−1时群速度的大小大约0.0008c(插图点划线).当纵波光学声子耦合强度0.45×1012s−1<κ<1.3×1012s−1(区间宽度为0.85×1012s−1)时,纵波光学声子耦合效应对孤子群速度存在较为明显的调节效果,尤其当κ≈1.0×1012s−1时群速度可调范围大致由−0.1c变为+0.1c.
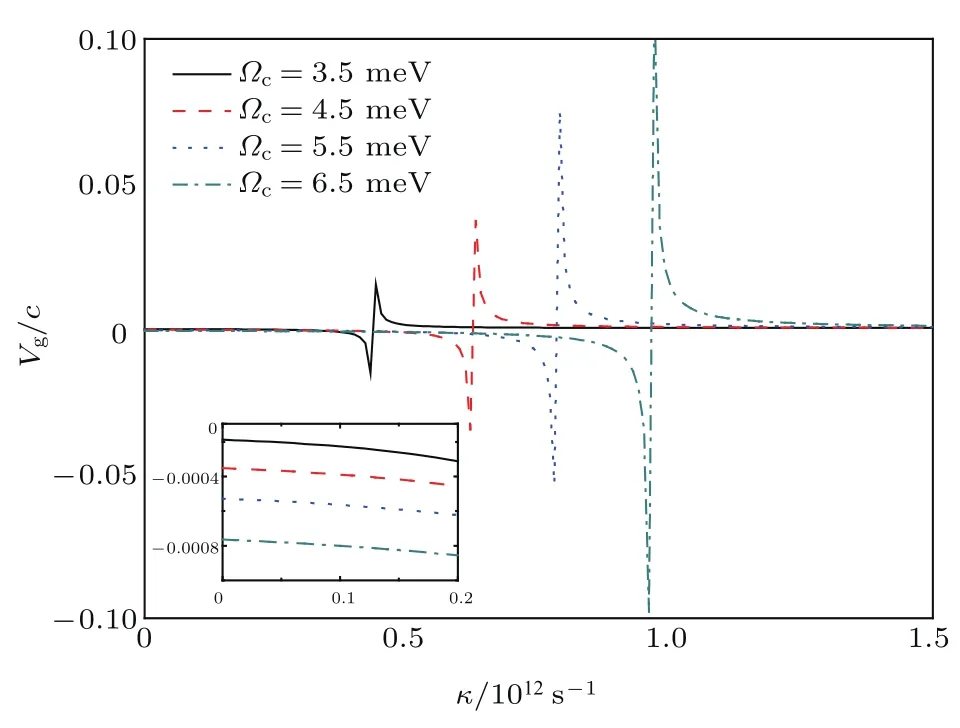
图5 (网刊彩色)孤子的群速度随纵波光学声子耦合强度的变化Fig.5.(color on line)The groupvelocity of the soliton as a function of the coeffi cient of cross-coupling relaxation of longitudinal optical phononsκ.
综上所述,在级联型三能级量子阱中我们不仅实现了孤子群速度的超慢传输;还通过调节纵波光学声子耦合强度实现了一定大小范围内群速度正负的转换,并且随着控制光场强度的增加,纵波光学声子耦合强度对群速度正负的影响效果越明显,而所对应的纵波光学声子耦合强度的有效调节范围就越大.事实上,保持控制光场不变时,若纵波光学声子耦合强度较小,光孤子在介质中表现出反常色散,此时光孤子群速度为负;但纵波光学声子耦合强度较大时,光孤子在介质中表现出正常色散,此时光孤子群速度为正.这些光孤子群速度峰值的跃变,是因为此时体系的纵波光学声子耦合强度恰好能使光孤子在介质中由反常色散过渡到正常色散,也就是群速度由负变为正,此时孤子群速度也就必然存在一个跃变的过程.另外,群速度的正负代表孤子在空间上的传播方向,负的群速度表示群速度的方向与规定的正方向相反.纵波光学声子耦合强度之所以能够对孤子群速度的正负和大小起调节作用,是因为孤子群速度与介质的色散关系有直接的联系.而纵波光学声子可以通过辅助跃迁的效应引起能级粒子布局的改变,进而影响体系内的量子相干与干涉效应,改变探测光在介质中的色散关系,实现对光孤子群速度的调节.
5 结 论
基于现有的实验条件,我们研究了纵波光学声子交叉耦合效应对级联型三能级量子阱中光孤子类型和群速度的影响.首先,在相互作用表象中我们用麦克斯韦-薛定谔方程组描述了光与级联型三能级量子阱之间的相互作用.随后,运用多重尺度法解析求解该方程组,且通过简化获得了一个标准的NLS方程,并求出其光孤子解.数值计算表明:在级联型三能级量子阱中,暗孤子和亮孤子在体系中均具有良好的稳定性.纵波光学声子耦合强度的大小能有效调控体系中所形成的暗-亮孤子的类型.在级联型三能级半导体量子阱中,我们不仅实现了孤子群速度的超慢传输,还通过纵波光学声子耦合强度的调节,实现了一定大小范围内群速度正负的转换.此外,控制光的强度越大,纵波光学声子耦合强度对群速度正负的大小效果越明显,并且相应的纵波光学声子耦合强度能有效调节群速度的变化范围.这为实验中如何操控半导体量子阱中的孤子提供了理论依据.
[1]Harris S E 1997Phys.Today50 36
[3]Kang H,Zhu Y 2003Phys.Rev.Lett.91 093601
[4]Tassin P,Zhang L,Koschny T,Economou E N,Soukou lis C M2009Phys.Rev.Lett.102 053901
[5]W ang B,Li S J,Chang H,W u HB,X ie C D,W ang H2005Acta Phys.Sin.54 4136(in Chinese)[王波, 李 淑静,常宏,武海斌,谢常德,王海2005物理学报54 4136]
[6]Kasapi A,Jain M,Y in G Y 1995Phys.Rev.Lett.74 2447
[7]X iaoM,Li Y,Jin S,Gea-Banacloche J 1995Phys.Rev.Lett.74 666
[8]Schmid t O,W ynands R,Hussein Z,Meschede D 1996Phys.Rev.A53 R27
[9]Hau L V,Harris SE,Zachary D,Cyrus HB1999Nature397 594
[10]W u Y,Wen L,Zhu Y 2003Opt.Lett.28 631
[11]Chen Y,Bai Z,Huang G 2014Phys.Rev.A89 023835
[12]Huang G,Deng L,Payne MG 2005Phys.Rev.E72 016617
[13]W u Y,Deng L 2004Phys.Rev.Lett.93 143904
[14]W u HB,Chang H,Ma J,Xie C D,Wang H2005Acta Phys.Sin.54 3632(in Chinese)[武海斌,常宏,马杰,谢常德,王海2005物理学报54 3632]
[15]Liu C,Dutton Z,Behroozi C H,Hau L V 2001Nature409 490
[16]Yang W X,Hou J M,Lin Y,Lee R K2009Phys.Rev.A79 033825
[17]Paspalakis E,Tsaousidou M,Terzis AF 2006Phys.Rev.B73 125344
[18]Li J H2007Phys.Rev.B75 155329
[19]W u J H,GaoJ Y,Xu J H,Silvestri L,Artoni M,La Rocca G C,Bassani F 2005Phys.Rev.Lett.95 057401
[20]AsanoT,Noda S,Abe T,Sasaki A1996Jpn.J.Appl.Phys35 1285
[21]Yang W X,Lee R K2008Opt.Express16 17161
[22]Neogi A,Yoshida H,Mozume T,W ada O1999Opt.Commun.159 225
[23]LuoX Q,W ang D L,Zhang Z Q,D ing JW,Liu W M2011Phys.Rev.A84 033803
[24]Tang H,W ang D L,She Y C,D ing JW,X iaoSG 2016Eur.Phys.J.D70 22
[25]Huang J L,Xu JZ,X iong Y T2004Soliton Conceptions,Theory and Application(1st Ed.)(Beijing:Higher Education Press)p96(in Chinese)[黄景宁,徐济仲,熊吟涛2004孤子概念、原理和应用(第1版)(北京:高等教育出版社)第96页]
[26]Yang W X,Hou J M,Lee R K2008Phys.Rev.A77 033838
[27]She Y C,Zheng X J,W ang D L,Zhang W X 2013Opt.Express21 17392
[28]Dynes J F,Frogley MD,Beck M,Faist J,Phillips C C 2005Phys.Rev.Lett.94 157403
[29]She Y C,W ang D L,Zhang W X,He Z M,D ing JW 2010J.Opt.Soc.Am.B27 208
[30]Hang C,Li Y,Ma L,Huang G X 2006Phys.Rev.A74 012319
[31]Zhu C J,Huang G X 2009Phys.Rev.B80 235408
[32]Zhang B,W ang D L,She Y C,Zhang W X 2013Acta Phys.Sin.62 110501(in Chinese)[张波,王登龙,佘彦超,张蔚曦2013物理学报62 110501]
[33]Roskos HG,Nuss MC,Shah J,LeoK,Miller D AB,Fox AM,Schmitt-Rink S,Köh ler K1992Phys.Rev.Lett.68 2216
PACS:42.65.Tg,42.81.Dp,73.21.Fg,78.67.DeDOI:10.7498/aps.66.034202
Controlling of dark or b right soliton type in a cascade-type electromagnetically induced transparency semiconductor quantumwell by the coupling longitud inal optical phonons∗
Tang Hong1)Wang Deng-Long1)†Zhang Wei-Xi2)Ding Jian-Wen1)XiaoSi-Guo1)
1)(School of Physics and Optoelectronics,X iangtan University,X iangtan 411105,China)2)(College of Physics and E lectronic Engineering,Tongren University,Tongren 554300,China)
(Received 19 April 2016;revised manuscript received 3 October 2016)
In the past fewyears,with developing the technology of electromagnetically induced transparency(EIT)and improving the semiconductor technology,it has become possible torealize the application of optical soliton tocommunication device.Studies showthe reduction of groupvelocity of the optical soliton in EITmediumunder weak d riving condition,which possib ly realizes the storing of optical pulses in information storage.More importantly,semiconductor quantumwells have the inherent advantages such as large electric dipole moments of the transitions,high non linear optical coeffi cients,small size,easily operating and integrating.Soit is considered tobe themost potential EITmediumtorealize the application of quantumdevices.The optical soliton behavior in the semiconductor quantumwell is studied,which can provide a certain reference value for the practical application of information transmission and processing together quantumdevices.
Although there has been a series of researches on both linear and nonlinear optical properties in semiconductor quantumwells structures,fewpub lications report the eff ects of the cross-coupling longitude-optical phonon(CCLOP)relaxation on its linear and nonlinear optical properties.However,toour knowledge,the electron-longitude-optical phonon scattering rate can be realized experimentally by varying the sub-picosecond range tothe order of a picosecond.According tothis,we in the paper study the eff ectsof the CCLOP relaxation on its linear and nonlinear optical properties in a cascade-type three-level EITsemiconductor quantumwell.
According tothe current experimental conditions,we fi rst propose a cascade-type three-level EITsemiconductor quantumwellmodel.And in thismodel we consider the longitudinal optical phonons coupling between the bond state and anti-bond state.Subsequently,by using themultiple-scalemethod,we analytically study the dynamical propertiesof solitons in the cascade-type three-level EITsemiconductor quantumwell with the CCRLOP.It is shown that when the CCRLOP strength is smaller,there exhibits the dark soliton in the EITsemiconductor quantumwell.Only if the strength of the CCRLOP is larger,will in the systemthere exists bright soliton.That is tosay,with increasing the strength of the CCRLOP,the soliton type of the systemis converted fromdark tobright soliton little by little.So,the temporal soliton type can be eff ectively controlled by the strength of the CCRLOP.In addition,we alsofind that the groupvelocity of the soliton can alsobe controlled by the strength of CCRLOP and the control light.These resultsmay provide a theoretical basis for manipu lating experimentally the dynamics of soliton in semiconductor quantumwells.
cross-coupling relaxation of longitudinal optical phonons,electromagnetically induced transparency,semiconductor quantumwells
10.7498/aps.66.034202
∗国家自然科学基金(批准号:11474245,11374252,51372214)和贵州省教育厅自然科学研究项目(批准号:KY(2015)384,KY(2015)446)资助的课题.
†通信作者.E-mail:d lwang@x tu.edu.cn
*Project supported by the NationalNatural Science Foundation of China(Grant Nos.11474245,11374252,51372214)and the Scientifi c Research Fund of Guizhou Provincial Education Department,China(G rant Nos.KY(2015)384,KY(2015)446).
†Corresponding author.E-mail:d lwang@xtu.edu.cn
