面向加工效率的曲面刀具路径优化方法*
2017-07-31邓兴国何其林
邓兴国,李 丽,何其林
(西南大学 工程技术学院,重庆 400715)
面向加工效率的曲面刀具路径优化方法*
邓兴国,李 丽,何其林
(西南大学 工程技术学院,重庆 400715)
针对曲面数控加工中加工效率低的问题,提出了一种提高曲面类零件加工效率的刀具路径优化方法。首先对刀具路径优化问题进行描述,提出了刀具路径与加工效率的关系模型;再建立了以机床加工效率为优化目标,以主轴转速、进给量、切削功率、主轴力矩、加工行距为约束的优化模型;并根据曲面加工行距和加工质量的影响,对曲面离散化而生成合理的刀触点;利用蚁群算法对刀触点的连接顺序及无重复走刀方式进行优化求解。最后通过案例验证了该方法的有效性。
刀具路径优化;加工效率;蚁群算法;约束
0 引言
随着现代产品制造业对零件切削加工“高效率”、“高精度”和“环境友好型”等方面的要求越来越高,数控加工已成为应用越来越广泛的机械加工方法。目前,许多学者针对数控加工中切削参数优化[1]、工艺路线规划[2]等方面进行了大量研究;然而对数控加工中刀具路径规划(如加工间距、路径长度等)方面的研究较少。
如何通过生成合理的刀具路径来提高加工效率和保证加工质量受到国内外学者的广泛关注。Oysu C等[3]提出了一种基于混合遗传算法的刀具路径优化方法,对曲面加工中的走刀空行程进行了优化;Manav C等[4]提出了一种基于多准则优化方法的刀具路径规划方法,对曲面加工中受平均合力、残留高度和加工时间三者影响的刀具路径进行了优化;黄琴等[5]提出了一种基于等误差步长规划方法的刀具路径优化方法,解决了三角网格曲面加工刀具轨迹的误差均匀性问题;赵鹏等[6]提出了一种基于非均匀B样条曲线拟合的刀具路径优化方法,解决了曲面加工中刀具路径不连续问题;季国顺等[7]提出了一种基于蚁群算法和最近邻算法相结合的刀具路径优化方法,对多轮廓加工的走刀空行程进行了优化;陈琳等[8]提出一种基于蚁群算法和贪心算法相结合的混合优化算法,对不同规格孔群加工的走刀空行程进行了优化;Medinarodriguez N等[9]则提出了一种基于并行方案的蚁群优化算法,优化得到了孔加工的最佳G代码命令、最短刀具路径和最优加工顺序。以上研究成果主要对曲面加工中走刀空行程、刀具路径轨迹不连续等方面的研究,或是针对孔群加工中最短加工路径、走刀空行程的优化研究,鲜有涉及在保证加工质量和考虑加工效率前提下,直接运用优化算法对曲面离散化生成刀触点而形成最优刀具路径的研究。
基于此,本文以曲面加工刀具路径为优化研究对象,结合加工行距、加工质量等影响因素,将曲面离散化以生成合理的刀触点数,再运用蚁群算法对曲面上刀触点连接顺序及无重复走刀进行优化求解,最后通过案例对其进行验证。
1 问题描述
1.1 刀具路径的数学描述
刀具路径是指为加工出工件外形刀具必须经过的刀位轨迹,由一个个离散刀位数据按实际加工过程中的运动顺序组成,可将刀具路径看成刀位数据的集合体[10]。该集合体里包含了CL点(Cutter Location Point,刀具位置点),且每个CL点对应一个CC点(Cutting Contact Point,刀触点),CC点由曲面离散化生成,用Ci,j={C0,1,C0,2,C1,1,...,Cn,m}表示,其中i=0,1,2,...,n;j=0,1,2,...,m;且没有重复点生成,即C0,0≠C0,1≠C1,1≠...≠Cn,m。曲面加工过程就是选取合适的铣削刀具沿刀位数据集合体里的刀触点进行无重复切削,所有刀触点的有效连接则构成了曲面加工刀具路径,用L表示:

(1)
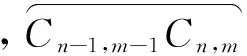
1.2 刀具路径影响因素分析
刀具路径包括实际切削路径Lc和空切路径Le(如刀具进退刀、快速进给等辅助走刀路径),本文研究的刀具路径L=Lc+Le,空切路径Le指超出工件加工范围空走刀部分的路径长度。影响刀具路径长度的主要因素如下:
(1)刀触点个数。曲面离散化生成的刀触点个数主要受曲面加工精度、刀具半径等影响。
(2)进给步长。同一条刀具路径上相邻两个刀触点间的距离即进给步长,其长度与曲面离散化生成刀触点间的距离有关,如图1所示。

图1 刀触点、加工行距与刀具半径、曲率半径、残留高度间关系图
(3)刀触点连接顺序与连接重复性。任意两刀触点间的连接顺序与连接的重复性决定了刀具路径的总长度,刀触点连接超出曲面边界部分决定了Le的长度。
(4)加工行距。加工行距是相邻两条刀具轨迹间对应刀触点间的距离,用l表示,如图1所示。l的大小主要受刀具半径R、加工残留高度h以及垂直于进刀方向的法曲率半径ρ所影响,并决定着刀具路径总长度。
1.3 刀具路径优化相关假设
为提高机床加工效率和优选出由刀触点最优连接顺序及无重复连接生成的刀具路径,为此在进行刀具路径优化前,作了如下假设:
(1)刀具路径优化前提是在数控机床、装夹方式、切削用量、工艺路线、刀具型号已经确定且加工环境相对稳定下,对刀具路径L进行有关加工效率的优化研究。
(2)数控加工中切削三要素根据大量切削参数优化研究,并结合实际加工需求进行了最优选择。
(3)工件加工工序为单工步、不换刀且无切削液情况下进行刀具路径优化。
2 优化模型
2.1 目标函数
本文研究目的是在确保曲面加工质量前提下,以机床加工效率为优化目标进行的刀具路径优化,因而目标函数为:
(2)
式中,w1、w2是加工效率与实际刀具路径和空切路径的影响权重,且w1+w2=1。
在数控加工中,提高加工效率也即缩短工件的加工时间。根据文献[11]知,完成一个零件铣削加工工序的加工时间主要包括机床待机时间tst、切削时间tcut、换刀时间tct、空切时间tair四部分,其加工时间函数表达式为:

(3)
式中,tpct为单次磨钝换刀时间,Tc为刀具寿命,fv为进给速度,n为主轴转速,Z为刀具齿数,fz为每齿进给量,Lcut和Lair分别为实际切削路径和空切路径。由于本研究只考虑一把刀具加工,加工过程不出现换刀现象,则得出tct与刀具路径的长短无关,而tst主要与操作人员技术水平熟练程度有关,故本文对tct与tst不作研究。本文重点研究由实际切削路径和空切路径组成的刀具路径,根据1.1节、1.2节的描述得L=Lc+Le,则可得出刀具路径与机床加工效率间的数学模型:

(4)
从上式可以看出,刀具齿数Z由所选铣削刀具决定,主轴转速n和每齿进给量fz则可根据切削参数优化研究选取最优值,从而得出直接影响机床加工效率的就是刀具路径长度大小。并且在实际加工过程中,加工刀具路径是根据操作人员的加工经验及切削手册设定相应参数后由CAM软件生成,同时操作人员很少关注切削路径长度对加工效率的影响,其刀具路径长度并未经过优化处理,进而形成了一种固定模式加工,加工效率未得到改善,因此在实际加工中优化刀具路径,减少其长度,对缩短加工时间,提高加工效率具有重要的实际应用意义。
2.2 约束条件
数控加工过程中,由于受所选机床主轴转速、进给量、机床功率以及工件加工质量等限制,因此在进行曲面刀具路径优化时,应满足以下约束条件:
(1)主轴转速约束。数控加工时根据不同刀具直径对应都有一个确定的切削速度范围,即:

(5)
式中,D—刀具直径,nmin—机床最低主轴转速,nmax—机床最高主轴转速。
(2)进给量约束。进给量必须在机床所允许的范围内,即:
fmin≤f≤fmax
(6)
式中,fmin—机床所允许的最小进给量,fmax—机床所允许的最大进给量。
(3)切削功率约束。进行工件加工时,切削功率应小于机床规定的有效功率,即:

(7)
式中,η—机床效率有效系数,Fc—切削力,Pmax—机床最大功率。
(4)主轴力矩约束。数控铣削加工过程中,机床主轴力矩应小于机床主轴所允许的最大力矩[12],即:

(8)
式中,D—刀具直径,Mj—机床主轴允许的最大力矩。
(5)加工行距约束。加工行距直接关系到离散点的数量,进而影响刀具路径的长短;由于加工行距受表面加工质量的影响,因此,加工行距在小于允许值的前提下,还必须满足表面加工质量,即:
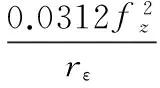
(9)
式中,rε—刀尖圆弧半径,Rmax—零件表面粗糙度最大值。
2.3 优化模型
通过以上分析,在满足所有约束条件下,得出以加工效率为优化目标的刀具路径优化数学模型如下:

(10)
式中,w1、w2是加工效率与实际切削路径和空切路径的影响权重,且w1+w2=1,其权重值可根据层次分析法、模糊评价法等进行确定,本文对实际切削路径和空切路径的优化权重均等,所以取值分别为w1=0.5、w2=0.5。
3 优化模型求解
刀具路径优化的本质是一种路径寻优问题,因此本文利用全局优化能力强、搜索速度快的蚁群算法进行模型求解,根据1.2节的描述,本文将刀具路径优化求解分为两步:第一步根据曲面曲率、刀具半径、残留高度离散曲面,优化出合理的刀触点数;第二步利用蚁群算法进行曲面加工刀触点连接顺序及无重复走刀优化求解,以寻求最优刀具路径。下面对其关键步骤做进一步介绍。
3.1 刀触点数优化求解
本文把待加工曲面用NURBS曲面方法进行表示[13],构建的曲面模型如图2所示。再根据进刀方向法曲率半径ρ、刀具半径R以及曲面加工后残留高度h,把待加工的曲面进行最优离散化,从而得到合理的曲面离散点,以各离散点作为刀具加工路径的刀触点。设曲面上任意点的法矢为:

(11)
Su是相对于u向上的曲面方程的偏导数,Sv是相对于v方向上的曲面方程的偏导数。给定一条路径曲线C(t)=S(u(t)+v(t)),t是沿路径的独立变量,路径间隔上的曲率半径计算如下[14]:
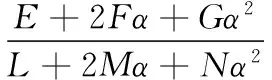
(12)

如图1所示,由△oad∽△obc,则有:
(13)
相应线段的计算式为:
(14)
(15)
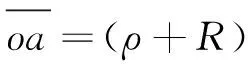
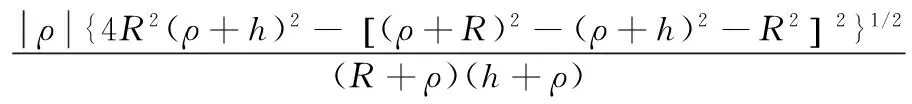
(16)
其中,ρ>0表示曲面为凸曲面,ρ<0表示曲面为凹曲面。


(a)曲面模型正面 (b)曲面模型反面
图2 曲面模型
3.2 刀触点连接顺序及无重复走刀优化求解
蚁群算法是模拟自然界中蚂蚁群体觅食过程而形成的一种新型智能算法,其最初由意大利学者Dorigo M于1991年提出,并将该算法用于求解TSP问题、指派问题以及车间调试问题等,取得了良好的效果。
蚂蚁觅食时,会在经过的路径上释放信息素,并能感知信息素的存在。大量蚂蚁相互协作,通过信息素的浓度来指引其觅食方向,路径上信息浓度越大,蚂蚁选择该路径的机率就越大,使该路径上的信息素浓度进一步增强,进而形成一种正反馈机制,最后通过该正反馈机制找出最短路径[15]。本文以此为基础来寻求曲面加工过程中的最短刀具路径,以缩短加工时间,提高加工效率。
3.2.1 刀触点间转移概率函数
运用蚁群算法进行刀具路径寻优时,主要根据转移概率函数来选择刀具需经过的下一个刀触点,以确保各刀触点间的最优连接。在t时刻,蚂蚁k从刀触点Cn-1 , m-1转移到Cn , m的概率为[16-17]:
(17)

3.2.2 无重复走刀禁忌表设置
为确保得到最优刀具路径,在刀具路径寻优过程中,刀触点应无重复连接,每个刀触点只允许遍历一次,对此为蚂蚁设置了相应的禁忌表tabuk,以避免重复走刀。蚂蚁k每经过曲面上一个刀触点后,将其记录标记并存放在自己的tabuk中,表示该位置处的刀触点已经被蚂蚁访过,防止蚂蚁再次访问而形成重复走刀。当所有刀触点都被存放到tabuk中时,则表示蚂蚁k完成了一次循环。当本次循环结束后,禁忌表用来计算蚂蚁当前所建立的空间路径(即蚂蚁所经过的路径长度)。之后,禁忌表被清空,蚂蚁又开始进行下一次循环。
3.2.3 刀具路径信息素更新
当所有蚂蚁完成一次路径寻优循环后,为避免残留信息素过多造成残留信息覆盖启发信息,则需对各刀具路径上的信息素进行更新,以便完成下次循环操作。
各路径上信息素量根据下式进行更新[16-17]:
τij(t+n)=(1-ρ)·τij(t)+Δτij(t)
(18)
(19)
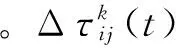
(20)
式中,Q为信息素强度,Lk为第k只蚂蚁本次循环中所走的路径长度。
通过上述分析,得出刀具路径优化具体实施步骤如下:
(1)曲面模型构建、加工行距控制,待加工曲面离散化生成刀触点。
(2)参数初始化。令初始时间t=0和初始循环次数Nc=0,设置最大循环次数Ncmax,对每条路径(Ci,j,Ci′,j′)设置τij(t)=C(C取较小常数值),且初始时刻Δτij(0)=0,设置α、β、Q以及每只蚂蚁的禁忌表tabuk。
(3)循环次数Nc=Nc+1。
(4)蚂蚁禁忌表初始索引号k=1。
(5)蚂蚁数k=k+1。
(6)第k只蚂蚁开始寻找曲面加工最短路径,根据公式(17)选择刀触点i并继续向前搜索。
(7)把经过的刀触点i添加到第k只蚂蚁的禁忌表tabuk中,以确保不被再次访问。
(8)若第k只蚂蚁遍历完了刀触点,则继续执行第(9)步,否则返回第(6)步。
(9)若蚂蚁数k小于蚂蚁总数m,则返回第5步,直到m只蚂蚁遍历完所有的刀触点后,再执行第(10)步。
(10)根据公式(18)、公式(19)进行每条路径上信息量更新,找出m只蚂蚁中所走的最短路径值并保存。
(11)若满足约束条件,即Nc≥Ncmax,则结束循环并输出最短路径值,否则清空禁忌表并返回第(4)步。
优化求解流程图如图3所示。

图3 优化求解流程图
4 案例验证
本文提出的刀具路径生成方法主要利用MATLAB实现,通过MasterCAM生成相应刀具路径,并采用在相同参数设置条件下的不同加工方式生成的刀具路径作对比,以验证本方法的可行性。本文研究的重点是曲面模型半精加工阶段的刀具路径优化。
4.1 刀触点个数优化结果
图2为建立的曲面模型,模型直径d=36 mm。通过曲率分析得曲面凹处最大法曲率kmax=0.31,待加工曲面表面粗糙度要求为不超过6.5μm,由前面的描述得到半精加工阶段球头铣刀的半径取R=3 mm,则由式(16)得l=0.86 mm。按照等参数线采样法对曲面进行离散,得到合理的控制点共1075个,即刀触点数为1075个,离散结果如图4所示。

图4 离散化曲面
4.2 刀具路径优化结果
采用MATLAB进行蚁群算法曲面刀具路径寻优计算。参数设置为:蚂蚁数m=40,信息启发式因子α=1,期望启发式因子β=2,信息素挥发因子ρ=0.7,信息素强度Q=500,最大循环次数Ncmax=300,循环次数初始值Nc=0。通过计算得到了图5a所示的所有刀触点形成的最优且无重复连接的刀具路径图;图5b为蚁群算法计算最优刀具路径的收敛图,从图中可得,算法初期收敛性较差,随着循环次数的递增,收敛趋于平稳,且在289次时,得到刀具路径最优值为1586.53 mm。
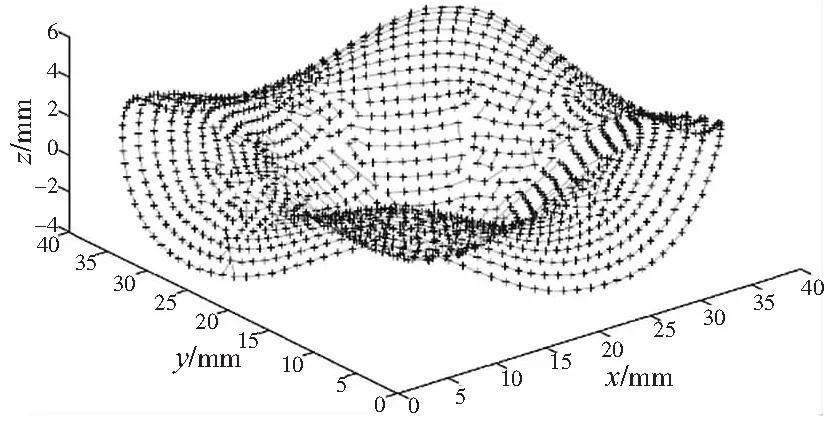
(a)路径图
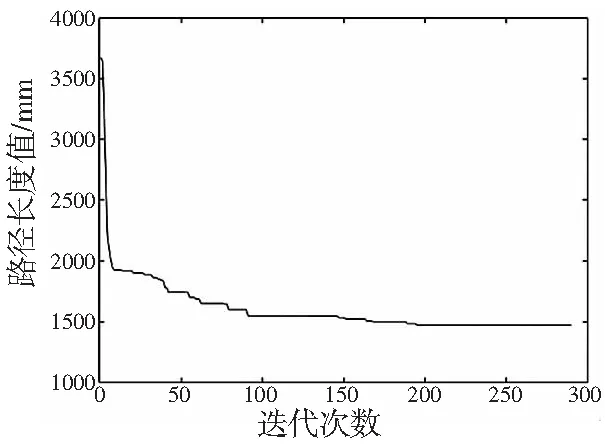
(b)收敛过程图
4.3 结果分析
曲面模型的刀具路径由MasterCAM数控编程软件生成,并选择平行铣削和流线型铣削生成的刀具路径作为本文刀具路径的仿真对比对象。曲面模型粗加工均采用等高轮廓铣,以最快速度去除材料,刀具半径R=5 mm,加工余量均留为0.5 mm。半精加工阶段参数设置:刀具半径R=3 mm,切削深度ap=0.3 mm,主轴转速n=3000 r/min,进给量F=500 mm/min。
采用本文提出的刀具路径生成方法与MasterCAM数控编程软件的不同路径生成方式得到了如图6所示的刀具路径图,图中曲面内的蓝色线条为刀具切削路径,曲面外的蓝色线条为刀具空切路径。各方式下生成的刀具路径长度、切削时间如表1所示。
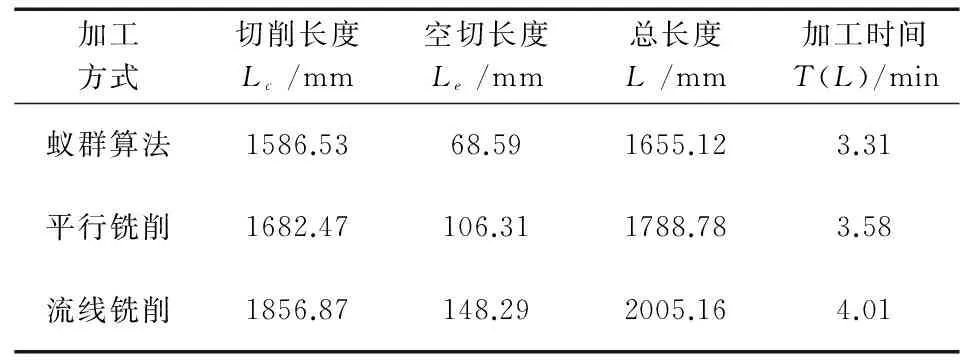
表1 各切削刀具路径值比较

图6 不同方式的刀具路径图
(1)从图6可以看出,本文提出的面向加工效率的刀具路径规划方法可行且路径生成连续性较好,铣削刀具通过该加工路径时能完整地遍历整个曲面,空切路径部分较少。
(2)本方法所生成的刀具路径在切削长度和空切长度上较其他两种路径生成方式都有明显的优势,从表格数据来看,切削长度最大优化值为270.34 mm,相对减少14.56%,最短优化值为95.94 mm,相对减少5.70%;路径总长度方面,可以得出该方法生成的刀具路径优势更加明显,刀具路径总长度最大优化值为350.04 mm,相对减少17.46%,最短优化值为133.66 mm,相对减少7.47%。
(3)从表1数据来看,其他参数设置相同时,机床的加工效率主要受刀具路径长度影响,刀具路径越短,总切削时间越短,则加工效率越高,从而验证了该方法的可行性和有效性。
5 结论
为缩短曲面数控加工时间、提高生产效率,本文提出了以加工效率为目标,以主轴转速、进给量、切削功率、主轴力矩、加工行距为约束的优化模型,并利用蚁群算法对刀触点和刀具走刀方式进行优化求解,通过仿真数据对比,可见本文方法优化的刀具路径明显优于传统方法中的平行铣削及流线铣削刀具路径,其优越性主要体现在刀具路径长度以及加工时间两个方面。并且案例验证了将该方法运用于曲面模型刀具路径规划的可行性,达到了缩短数控加工时间,提高生产效率的目的,同时也为曲面类零件刀具路径优化问题开辟了一条新途径,为其奠定一定的理论基础。
[1] Li Li, Liu Fei, Chen Bing, et al. Multi-objective optimization of cutting parameters in sculptured parts machining based on neural network[J]. Journal of Intelligent Manufacturing, 2015,26(5): 891-898.
[2] 刘伟, 王太勇, 周明, 等. 基于蚁群算法的工艺路线生成及优化[J]. 计算机集成制造系统, 2010,16(7):1378-1382.
[3] Oysu C, Bingul Z. Application of heuristic and hybrid-GASA algorithms to tool-path optimization problem for minimizing airtime during machining[J]. Engineering Applications of Artificial Intelligence, 2009,22(3): 389-396.
[4] Manav C, Bank H S, Lazoglu I. Intelligent toolpath selection via multi-criteria optimization in complex sculptured surface milling[J]. Journal of Intelligent Manufacturing, 2013,24(2): 349-355.
[5] 黄琴, 杨旭静, 郑娟. 三角网格曲面加工刀具路径生成等误差步长算法研究[J]. 机械科学与技术, 2015,34(9): 1370-1374.
[6] 赵鹏, 楼佩煌, 刘明灯,等. 基于NURBS曲线拟合的刀具路径优化方法[J]. 计算机集成制造系统, 2011,17(7): 1454-1459.
[7] 季国顺, 王文, 陈子辰. 数控多轮廓加工走刀空行程路径优化[J]. 农业机械学报, 2008,39(7): 154-158.
[8] 陈琳, 刘晓琳, 潘海鸿, 等. 孔群分类加工路径的优化算法[J]. 制造业自动化, 2013,35(9): 46-49.
[9] Medinarodriguez N, Montielross O, Sepulveda R, et al. Tool Path Optimization for Computer Numerical Control Machines Based on Parallel ACO[J]. Engineering Letters, 2012,20(1):1-9.
[10] 陈良骥. 复杂曲面数控加工相关技术[M]. 北京: 知识产权出版社, 2011.
[11] 李聪波, 朱岩涛, 李丽, 等. 面向能量效率的数控铣削加工参数多目标优化模型[J]. 机械工程学报, 2016,52(21):120-129.
[12] 姜彬, 郑敏利, 李振加, 等. 球头铣刀切削力的预报[J]. 哈尔工大学学报, 2001,6(6): 20-24.
[13] 陈燕丽. NURBS复杂自由曲面造型方法的研究[D]. 西安: 长安大学, 2014.
[14] Chen T, Shi Z. A tool path generation strategy for three-axis ball-end milling of free-form surfaces[J]. Journal of Materials Processing Technology, 2008,208(1): 259-263.
[15] 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2005.
[16] 宋锦娟, 白艳萍. 基于改进蚁群算法的最短路径问题研究及应用[J]. 数学的实践与认识, 2013,43(3): 156-164.
[17] 詹士昌, 徐婕, 吴俊. 蚁群算法中有关算法参数的最优选择[J]. 科技通报, 2003,19(5): 381-386.
(编辑 李秀敏)
找检测仪器,请上
QC检测仪器网
WWW.QCtester.com
微信号:qctest
Tool Path Optimization with Machining Efficiency for Curved Surface
DENG Xing-guo, LI Li, HE Qi-lin
(College of Engineering and Technology, Southwest University, Chongqing 400715,China)
In view of the problem of low processing efficiency in NC machining of curved surface,a tool path optimization method is proposed to improve the machining efficiency of curved surface parts. Firstly,the problem of tool path optimization is described, and the relation model between the tool path and the processing efficiency is constructed, and a tool path optimization model is established which takes the machining efficiency as the optimization objective, with the constraints of the spindle speed, feedrate, cutting power, spindle torque and processing line.Then, according to the influencing factors of surface processing line and the machining quality, the reasonable cutter contact point is obtained through the surface discretization. Next, the connection order and the non-repetitive processing are optimized by using ant colony algorithm. Finally, the case results show that the method is effective.
tool path optimization;machining efficiency;ant colony algorithm;constraints
1001-2265(2017)07-0101-06
10.13462/j.cnki.mmtamt.2017.07.024
2016-09-14;
2016-10-22
国家自然科学基金资助项目(51451396);重庆市基础科学与前沿技术项目(cstc2016jcyjA1733);中央高校基本业务费专项资金资助(XDJK2016E053)
邓兴国(1992—),男,重庆合川人,西南大学硕士研究生,研究方向为绿色制造、数控加工,(E-mail)dxgjy0409@163.com;通讯作者:李丽(1982—),女,重庆人,西南大学副教授,硕士研究生导师,博士,研究方向为可持续设计与制造,现代设计方法,(E-mail)swulili@swu.edu.cn。
TH164;TG506
A
