基于修正矩阵的刚柔混合模型公差分析方法*

黄贺福，杨志宏，李 娜，张庚楠

(山东大学 机械工程学院，济南 250061)



基于修正矩阵的刚柔混合模型公差分析方法*

黄贺福，杨志宏，李 娜，张庚楠

(山东大学 机械工程学院，济南 250061)

为了在设计阶段进行公差分析、结构优化，文中讨论了刚柔混合模型的装配偏差，提出了一种基于修正矩阵的公差分析方法。将刚柔混合模型的理想位姿、公差域表示为矩阵形式，借助齐次变换进行公差累积。使用有限元模拟装配变形，将仿真结果表示为修正矩阵，对原有的偏差累积路径进行修正，从而实现了对刚柔混合模型关键尺寸的精确预测，为设计优化奠定了基础。以汽车车灯装配为例，验证了该方法的可行性。

公差分析；刚柔混合模型；齐次变换；有限元分析

0 引言

产品质量由设计、制造、装配三个环节共同控制。在制造过程中，零件的偏差是不可避免的。在装配过程中，偏差源经过累积、叠加后，影响着产品质量[1]。所以，在设计阶段进行公差分析、装配质量验证有重要的意义。

通常的，刚性件是指刚性好、厚度大的零件，其产生的装配变形可以被忽略；柔性件是指厚度远小于长度和宽度的板件，其在装配过程中会产生明显的变形。两者在偏差来源、公差分析方法等方面有着明显的不同。

刚性件的公差分析方法已经进行了多年的研究，典型的方法有封闭环模型、矩阵模型[2]、雅克比旋量模型[3]、T-MAP模型[4]等，这些方法的研究相对成熟，广泛应用于CAT领域中。针对柔性件的偏差研究始于80年代，Takezawa[5]对车身薄板件的装配数据运用回归分析，指出装配体偏差可能小于零件偏差，并接近于刚性较大的零件。Liu等[6]引入敏感度矩阵，建立了偏差源和装配偏差的线性关系。Hashemian等[7]综合考虑了夹具偏差、定位方案等因素对装配偏差的影响。Wooyoung 等[8]对焊接变形进行了研究。Wärmefjord[9]对焊接顺序进行了探索。Chen等[10]考虑了焊接方式对装配偏差的影响。Xie等[11]研究了装配过程中的接触干涉。Camelio等[12]探索了偏差源之间的关系，通过主成分分析，得到了装配偏差的统计分布图。

在工程应用中，刚性件和柔性件往往同时存在于产品中。现有的公差分析方法仅是针对刚性件或柔性件，并不适用于刚柔混合模型。本文以齐次变换为基础，通过有限元分析将装配变形表示为修正矩阵，修正原有的偏差累积路径，从而建立了统一的针对刚柔混合模型的公差分析方法，实现了对关键尺寸的精确预测。

1 刚柔混合模型

如果某个特征由单一元素组成，并且该元素限制此特征所有的自由度，那么该特征的理想位姿可以由依附在该元素上的坐标系来表示，而关键尺寸则可以借助坐标系间的转换进行计算。

柔性件在装配过程中容易因为定位、夹紧等操作导致变形。特征一旦产生了变形，其上建立的坐标系也将发生相应的变化。所以为了精确的计算出关键尺寸，必须对变化的坐标系进行修正。

根据设计信息，创建装配图，建立零件坐标系、特征坐标系，借助齐次变换将关键尺寸表示为位姿矩阵、公差矩阵的乘积。使用有限元模拟装配变形，将变形表示为修正矩阵，修正原有的关键尺寸表达式，实现了对关键尺寸的精确预测，其流程如图1所示。该方法可以应用于复杂的刚柔混合模型中，计算结果更为真实有效的反映出装配变形对关键尺寸的影响。

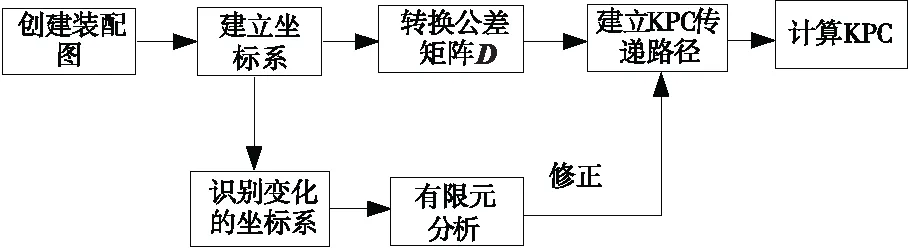
图1 刚柔混合模型偏差分析流程图

2 公差分析方法

2.1 基于齐次变换的公差累积

齐次变换可以将n维空间下矩阵的计算统一为(n+1)维空间下的叠乘，它广泛的应用于公差累积中。以图2所示的装配图为例说明齐次变换在公差累积中的应用。

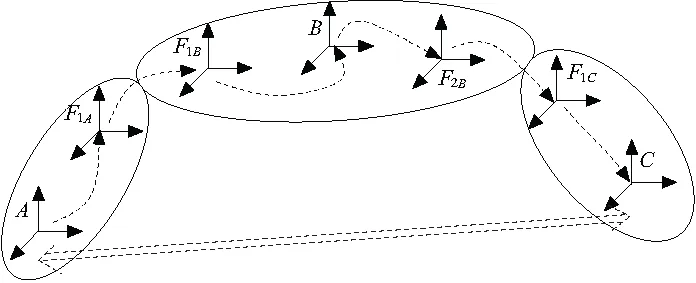
图2 装配图

图中，椭圆表示装配零件。A、B、C为零件坐标系，表示零件的位姿信息；F1A、F1B、F2B、F1C为特征坐标系，这些特征提供了装配约束；坐标系间的有向曲线表示偏差传递路径；双向线段为关键尺寸，用来评价装配质量是否达到要求。

(1)若零件A、B、C在制造和装配时没有任何偏差，则坐标系间的关系如图3所示。

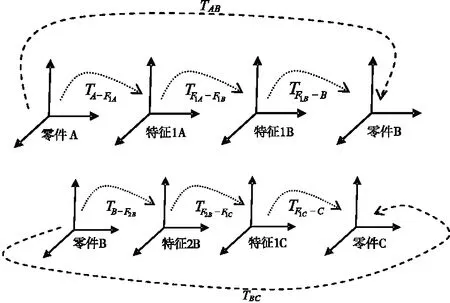
图3 无偏差坐标系关系示意图

则关键尺寸表示为：

TAC=TABTBC
TAB=TA-F1ATF1A-F1BTF1B-B
TBC=TB-F2BTF2B-F1CTF1C-C

式中，TA-F1A表示零件A的坐标系和特征F1A的坐标系之间的变换矩阵；TF1A-F1B为特征F1A的坐标系和特征F1B的坐标系之间的变换矩阵；所有的坐标系都建立在装配位置。

(2)若特征F2B存在定位偏差DB-F2B。则TBC修正为：

TB′C=TB-F2BDB-F2BTF2B-F1CTF1C-C

(3)若特征F2B存在形状偏差DF2B，则TBC变为：

TB′C=TB-F2BDF2BTF2B-F1CTF1C-C

(4)若特征F2B和F1C在装配过程中存在偏差DF2B-F1C，则TBC表示为：

TB′C=TB-F2BTF2B-F1CDF2B-F1CTF1C-C

综合三种偏差源，坐标系间的关系如图4所示。

图4 有偏差的坐标系关系示意图

借助齐次变换，包含全部偏差因素的关键尺寸为：

TAB=TA-F1ATF1A-F1BTF1B-B

TB′C=TB-F2B{[DB-F2B+DF2B]TF2B-F1C+TF2B-F1CDF2B-F1C}TF1C-C

TA′C=TABTB′CTA-F1ATF1A-F1BTF1B-BTB-F2B{[DB-F2B+DF2B]TF2B-F1C+TF2B-F1CDF2B-F1C}TF1C-C

2.2 修正矩阵

当特征坐标系建立后，该特征的任何变动都可以看作是绕坐标轴的平移和旋转。借助机器人运动学，特征的变动量可表示为修正矩阵M：

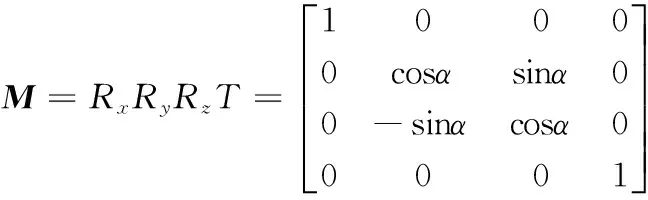
式中，T表示平移，R表示旋转；下标x,y,z表示方向；α,β,γ表示绕x,y,z旋转的角度；u,v,w表示在x,y,z上的平移量；s和c分别表示正弦和余弦函数。

在有限元中，根据实际装配情况施加边界条件以及载荷。将变形的特征坐标系原点与周围节点相关联，建立原点的变量输出。在模拟结果中读取相应的数值，进而计算修正矩阵。

假设图2中的零件A在装配过程中产生了变形，则需对特征F1A的坐标系进行修正。假设修正矩阵为M，则关键尺寸为：

TAC=TA-F1AMTF1A-F1BTF1B-BTB-F2B{[DB-F2B+DF2B]
TF2B-F1C+TF2B-F1CDF2B-F1C}TF1C-C

3 实例

图5所示为一车灯的装配实例。

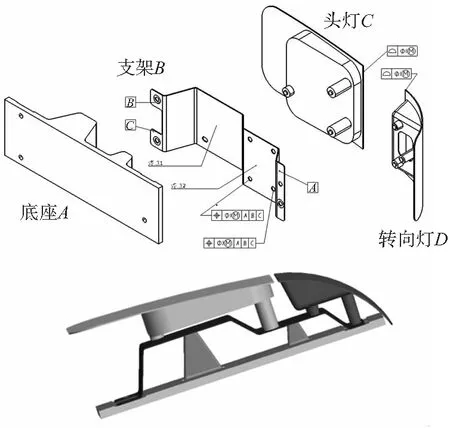
图5 车灯的装配实例

该模型有4个零件。材料属性：底座A, 头灯C, 转向灯D为刚性件；支架B的实际厚度是1.4mm，为柔性件，杨氏模量E=2.1×105N/mm2，泊松比v=0.3。装配方案：A和B通过3个螺栓以及2个焊点连接在一起。C和D借助3对孔销装配在(A+B)上。偏差源：假设A上两个焊接平面存在1mm的制造偏差(这里的设置是为了简化运算，其真实的偏差情况可以通过测量装置得到)。C和D的端面存在平面度公差1mm。B上的两个孔存在位置度公差1mm。B在装配时会因为焊点处的偏差产生变形。模型的关键尺寸为C和D端面的间隙。

关键尺寸可以按下列步骤进行计算：

(1)创建装配图；

(2)建立坐标系；

(3)将公差域转换为公差矩阵D；

(4)建立关键尺寸传递路径，如图6所示。

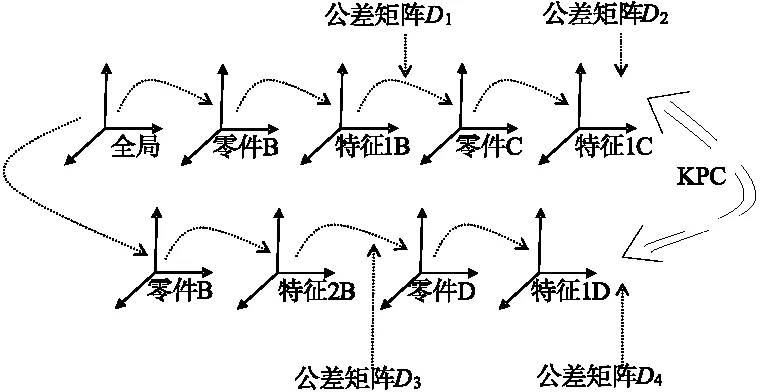
图6 关键尺寸传递路径

(5)识别变化的坐标系。模型中，B因变形导致了特征坐标系F1B和F2B的变化，其对应的修正矩阵表示为E、F。

(6)有限元分析。因为刚性零件A上的两个小平面存在制造偏差，所以焊接时柔性零件B上的两个焊点也会产生相应的1mm位移偏差，直接对焊点施加位移载荷。经过有限元操作，其变形如图7所示。利用模拟结果，计算修正矩阵E、F，如表1所示。

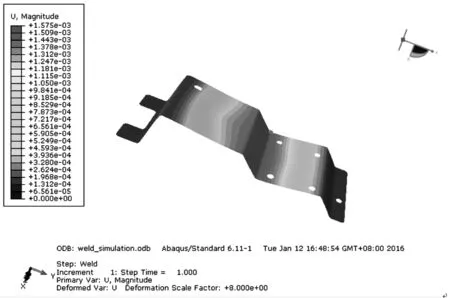
图7 变形示意图

E=11.2×10-2-7×10-41.362-1.2×10-2110-3-1.915×10-17×10-4-10-31-3.5×10-30001éëêêêùûúúúF=11.78×10-2-4×10-33.423×10-1-1.78×10-2110-4-1.82×10-14×10-3-10-41-7×10-40001éëêêêùûúúú

(7)修正原有的偏差累积路径。修正后的关键尺寸表达式为：

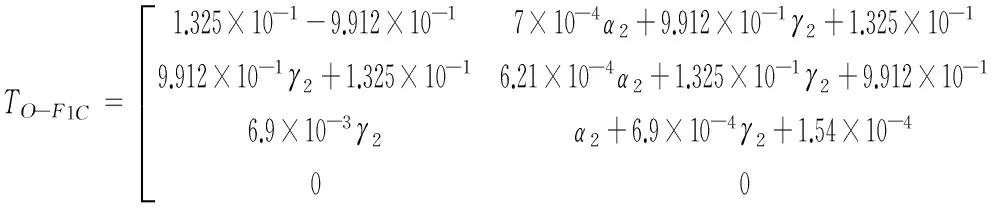
在公差域内随机取值5000次。同时，在不考虑装配变形(无修正矩阵M)的情况下随机取值5000次，关键尺寸的分布情况如图8所示。

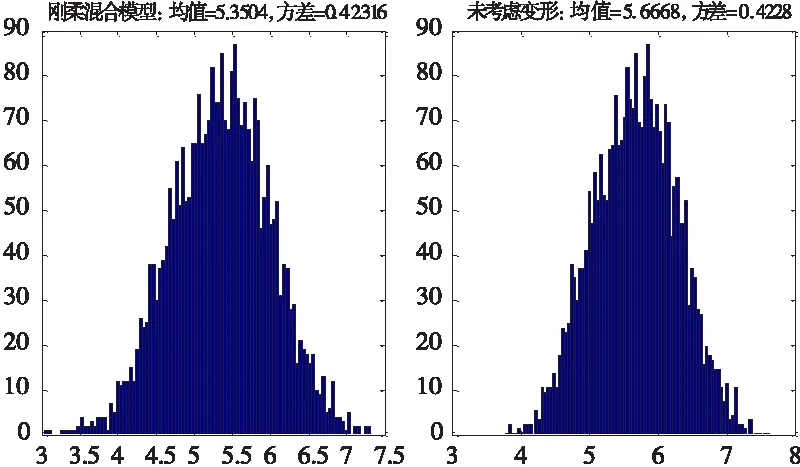
图8 关键尺寸分布图

3DCS是一款公差分析软件。运用该软件的柔性模块，对装配体进行偏差分析，如图9所示(A被简化为了约束点)。经过5000次模拟后得到关键尺寸的统计结果，将此结果和上述计算结果进行对比，如表2所示。

图9 3DCS模拟示意图

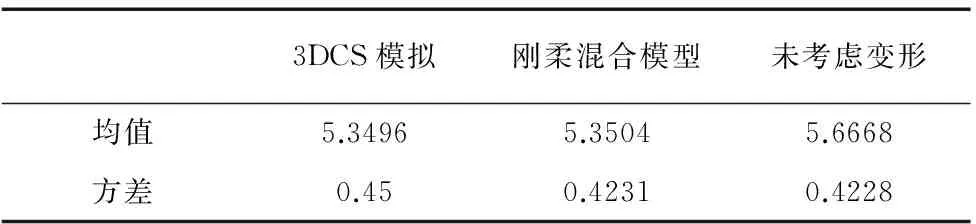
3DCS模拟刚柔混合模型未考虑变形均值5.34965.35045.6668方差0.450.42310.4228

结果分析：未考虑变形时，关键尺寸的均值和3DCS模拟结果的一致性为：5.6668/5.3496≈1.0592；文中所提方法的均值和3DCS模拟结果的一致性为：5.3504/5.3496≈1.0001。3DCS模拟和所提方法的结果具有更好的相符性，证明了该方法的有效性。可见，对于刚柔混合模型，该方法将装配变形引入到公差分析的计算中，实现了关键尺寸的精确预测。

4 总结

本文以齐次变换、有限元分析为基础，建立了基于修正矩阵的刚柔混合模型公差分析方法。

(1)借助机器人运动学、有限元分析，提出了修正矩阵的概念。利用有限元仿真结果，将装配变形表示为修正矩阵的形式，实现了偏差源信息更为全面的表述。

(2)借助齐次变换，建立了以理想位姿矩阵、公差矩阵以及修正矩阵为基础的偏差累积路径。案例结果表明，在刚柔混合模型中，装配变形是影响关键尺寸的重要因素之一。该方法将装配变形引入到公差分析的计算中，更为真实有效地预测出关键尺寸的分布情况。

(3)有限元分析是该方法的核心之一。如何根据实际装配情况建立简化的有限元模型、如何施加正确的边界条件、载荷等操作是机械设计人员亟需提高的技能。

[1] 魏建东, 李静蓉, 苏杭朋. 计算机辅助公差设计的开发及应用[J]. 组合机床与自动化加工技术, 2014(1):64-67.

[2] Marziale M, Polini W. A review of two models for tolerance analysis of an assembly: vector loop and matrix[J]. International Journal of Advanced Manufacturing Technology, 2009,43(11-12):1106-1123.

[3] Desrochers A, Ghie W, Laperrieère L. Application of a Unified Jacobian-Torsor Model for Tolerance Analysis[J]. Journal of Computing and Information Science in Engineering, 2003,3(1):2-14.

[4] Davidson J K, Mujezinovic′ A, Shah J J. A New Mathematical Model for Geometric Tolerances as Applied to Round Faces[J]. Journal of Mechanical Design, 2002,124(4):609-622.

[5] Takezawa N. An improved method for establishing the process-wise quality standard[J]. Rep. Stat. Appl. Res., JUSE, 1980,27(3):63-75.

[6] Liu S C, Hu S J. Variation Simulation for Deformable Sheet Metal Assemblies Using Finite Element Methods[J]. Journal of Manufacturing Science and Engineering, 1997,119(3):368-374.

[7] Hashemian A, Imani B M. An improved sensitivity-free probability analysis in variation assessment of sheet metal assemblies[J]. Journal of Engineering Design, 2014,25(10-12):346-366.

[8] Choi W, Chung H. Variation Simulation of Compliant Metal Plate Assemblies Considering Welding Distortion[J]. Journal of Manufacturing Science and Engineering, 2015,137(3):31008.

[9] Wärmefjord K, Söderberg R, Lindkvist L. Strategies for Optimization of Spot Welding Sequence With Respect to Geometrical Variation in Sheet Metal Assemblies[C]. ASME 2010 International Mechanical Engineering Congress and Exposition, 2010.

[10] Chen S, Lin Z, Zhang Y, et al. A parametric study of sheet metal joints for dimensional integrity[J]. International Journal of Advanced Manufacturing Technology, 2006,29(5-6):446-452.

[11] Xie K, Wells L, Camelio J A, et al. Variation Propagation Analysis on Compliant Assemblies Considering Contact Interaction[J]. Journal of Manufacturing Science and Engineering, 2007,129(5):934-942.

[12] Camelio J, Hu S J, Ceglarek D. Modeling Variation Propagation of Multi-Station Assembly Systems With Compliant Parts[J]. Journal of Mechanical Design, 2004,125(4):673-681.

(编辑 李秀敏)

A Unified Tolerance Analysis Method Based on Modified Matrix for Rigid-Compliant Hybrid Model

HUANG He-fu, YANG Zhi-hong, LI Na, ZHANG Geng-nan

(School of Mechanical Engineering, Shandong University, Jinan 250061,China)

For tolerance analysis and structure optimization in the design stage, this paper discusses assembly variation for rigid-compliant hybrid model. A unified tolerance analysis method based on modified matrix is proposed. Information of position, orientation of parts and tolerance zone are expressed in the form of matrix. The key product characteristic(KPC) is represented with the help of homogeneous transformation. The assembly deformation is simulated through finite element analysis (FEA) and the simulation result is used to modify the original variation buildup. The accurate prediction of the key product characteristic of rigid-compliant hybrid model is achieved, which lays the foundation for design optimization. A case study employing this methodology is presented and demonstrated by 3DCS software.

tolerance analysis; rigid-compliant hybrid model; homogeneous transformation; FEA

1001-2265(2017)07-0005-04

10.13462/j.cnki.mmtamt.2017.07.002

2016-10-15；

2016-11-13

国家自然科学基金资助项目(51375277)；山东省科技发展计划资助项目(2013GGX10303)

黄贺福(1991—)，男，内蒙赤峰人，山东大学硕士研究生，研究方向为公差分析与精度控制，(E-mail)imhefu@foxmail.com。

TH161;TG659

A