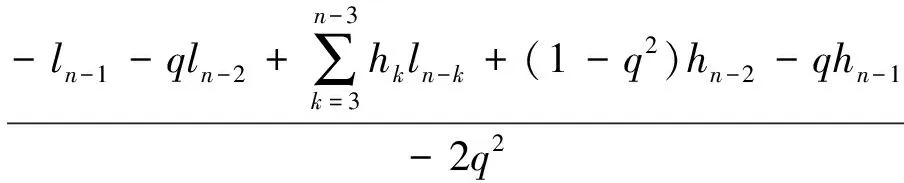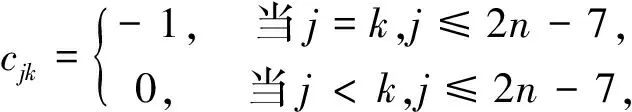一类含有3n个非零元的谱任意ray模式

霍英杰， 乔晓玲， 邵燕灵

(中北大学 理学院， 山西 太原 030051)

一类含有3n个非零元的谱任意ray模式

霍英杰， 乔晓玲， 邵燕灵

(中北大学 理学院， 山西 太原 030051)

利用矩阵特征值理论， 研究了一类含有3n个非零元的n阶ray模式矩阵. 在该ray模式矩阵的定性矩阵类中任取一个n阶复矩阵, 求出该复矩阵的特征多项式, 利用数学分析的方法， 找到该复矩阵为幂零矩阵的条件， 再运用幂零-雅可比方法， 证明了该类ray模式矩阵及其任意母模式都是谱任意的.

幂零-雅可比; ray模式; 谱任意; 蕴含幂零

1 预备知识

符号模式矩阵是指元素取自集合{+,-,0}的矩阵, 简称符号模式. 对于给定的实矩阵A=[aij], 由A中的每个元素aij的符号所确定的矩阵称为A的符号模式， 记为sgn(A). 对一个n阶符号模式A, 其定性矩阵类表示为

Q(A)={B|B为n阶实矩阵， 且sgn(B)=A}.

设A=(aij)和B=(bij)是两个n阶符号模式矩阵, 如果当bij≠0时aij=bij, 则称A=(aij)是B=(bij) 的母模式,B=(bij)是A=(aij)的子模式. 如果B≠A, 则称B是A的真子模式.

对n阶符号模式矩阵A, 如果存在B∈Q(A)和正整数k, 满足Bk=0且Bk-1≠0, 则称A蕴含幂零, 其中B为幂零矩阵,k为幂零矩阵B的指数, 并称B为A的一个幂零实现.

ray模式矩阵是指元素取自集合{eiθ∶0≤θ<2π}∪{0}的矩阵. 设P=(pij)是一个n阶ray模式,P的定性矩阵类表示为

Q(P)={A=[aij]∈Mn(C)∶aij=rijpij,

rij∈R+,1≤i,j≤n}.

若对任意的n次首1复系数多项式f(λ), 都存在复矩阵B∈Q(P), 使得B的特征多项式为f(λ), 则称ray模式矩阵P为谱任意的.

最早由文献[1]给出了谱任意符号模式矩阵的概念, 幂零-雅可比方法也是在该文献中提出的. 文献[2-11]对符号模式矩阵的谱任意性进行了深入的研究. 文献[12-15]将幂零-雅可比方法推广到复符号模式, 并对ray模式的谱任意性进行了研究.

2 N-J方法

引理 1[12](ray模式的幂零-雅可比方法)

1) 在ray模式P的定性矩阵类Q(P)中找到幂零矩阵B.

2) 用变量t1,t2,…,t2n替换B中的2n个eiθij的正系数(设为r1,r2,…,r2n).

3) 将替换后矩阵的特征多项式表示如下

λn+(f1(t1,…,t2n)+ig1(t1,…,t2n))λn-1+

…+(fn-1(t1,…,t2n)+ign-1(t1,…,t2n))λ+

(fn(t1,…,t2n)+ign(t1,…,t2n)).

5) 当(t1,t2,…,t2n)=(r1,r2,…,r2n)时, 若J的行列式不等于零, 则ray模式P及其任意母模式都是谱任意的.

3 主要结果

本文研究如下含有3n个非零元的n阶(n≥6)ray模式矩阵

将证明An及其任意母模式都是谱任意的.

任取复矩阵B∈Q(An),

|λI-B|=λn+α1λn-1+α2λn-2+…+αn-1λ+αn

其中，αk=fk+igk,k=1,2,…,n.

定理 1 矩阵B的特征多项式的系数为

证明

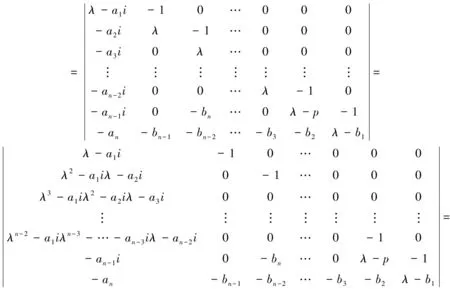
-bn-1(λ-a1i)+(λ2-a1iλ-a2i)[-bn(λ-b1)-bn-2]+(λ3-a1iλ2-a2iλ-a3i)(-bn-3)+

…+(λn-3-a1iλn-4-…-an-3i)(-b3)+(λn-2-a1iλn-3-…-an-2i)[λ2-(p+b1)λ+

(pb1-b2)]+[-an-ii(λ-b1)-an].

整理以上式子可得

证毕.

定理 2 ray模式矩阵An是蕴含幂零的.

证明

|λI-B|=

λn+α1λn-1+α2λn-2+…+αn-1λ+αn=

λn+(f1+ig1)λn-1+(f2+ig2)λn-2+…+

(fn-1+ign-1)λ+(fn+ign).

令fk=0,gk=0(1≤k≤n), 由定理1可得

lj的最低次数项

因此, 当0

由上易得

和

所以可得

当00,b1<0,bj>0(2≤j≤n-4),bn-3<0,bn-2<0,bn-1>0,bn>0.

所以ray符号模式矩阵An蕴含幂零.

证毕.

定理 3 ray符号模式矩阵An及其任意母模式都是谱任意的.

此时,tj(1≤j≤2n)均大于0, 易知:

det(C)=(-1)n+2det(C[{1,…,2n-7}])det(C[{2n-7,…,2n}])=

所以由引理1知， ray模式矩阵An及其任意母模式都是谱任意的. 证毕.

[1]Drew J H, Johnson C R, Olesky D D, et al. Spectrally arbitrary patterns[J]. Linear Algebra and its Applications, 2000, 308(1)： 121-137.

[2]Britz T, Mcdonald J J, Olesky D D, et al. Minimally spectrally arbitrary sign patterns[J]. SIAM Journal on Matrix Analysis and Applications, 2004, 26(1)： 257-271.

[3]Cavers M S, Vander Meulen K N. Spectrally and inertially arbitrary sign patterns[J]. Linear Algebra and its Applications, 2005, 394(1)： 53-72.

[4]Gao Y B, Shao Y L. A spectrally arbitrary pattern[J]. Advances in Mathematics, 2006, 35(5)： 551-555.

[5]Arav M, Hall F, Li Z, et al. Spectrally arbitrary tree sign patterns of order 4[J]. Electronic Journal of Linear Algebra, 2010, 20(2)： 180-197.

[6]Gao Y B, Shao Y L. Inertially arbitrary tree sign patterns of order 4[J]. Electronic Journal of Linear Algebra, 2011, 22(1)： 1148-1155.

[7]Behn A, Driessel K R, Hentzel I R, et al. Some nilpotent, tridiagonal matrices with a special sign patterns[J]. Linear Algebra and its Applications, 2012, 436(12)： 4446-4450.

[8]Garnett Colin, Shader B L. The Nilpotent-Centralizer method for spectrally arbitrary patterns[J]. Linear Algebra and its Applications, 2013, 438(10)： 3836-3850.

[9]Cavers M S, Fallat S M. Allow problems concerning spectral properties of patterns[J]. Electronic Journal of Linear Algebra, 2012, 23(1)： 731-754.

[10]Cavers M S, Garnett C, Kim I J, et al. Techniques for identifying inertially arbitrary patterns[J]. Electronic Journal of Linear Algebra, 2013, 26(1)： 71-89.

[11]Gao Y B, Shao Y L. The Nilpotent-Centralizer methods[J].Journal of Mathematical Research with Applications, 2014, 34(5)： 597-607.

[12]Mcdonald J J, Stuart J. Spectrally arbitrary ray patterns[J]. Linear Algebra and its Applications, 2008, 429(4)： 727-734.

[13]Gao Y B, Shao Y L. New classes of spectrally arbitrary ray patterns[J]. Linear Algebra and its Applications, 2011, 434(10)： 2140-2148.

[14]Mei Y Z, Gao Y B, Shao Y L, et al. The minimum number of nonzeros in a spectrally arbitrary ray pattern[J]. Linear Algebra and its Applications, 2014, 453(8)： 99-109.

[15]Zhang L, Huang T Z, Li Z S, et al. Several spectrally arbitrary ray patterns[J]. Linear and Multilinear Algebra, 2013, 61(4)： 543-564.

A Class of Spectrally Arbitrary Ray Patterns with 3nNonzero Entries

HUO Ying-jie， QIAO Xiao-ling， SHAO Yan-ling

(School of Science, North University of China, Taiyuan 030051, China)

Using matrix eigenvalue theory, a class ofn×nray pattern matrices with 3nnonzero entries was studied. Take anyn×ncomplex matrix belonged to the qualitative matrix class of the above ray pattern. The characteristic polynomial of this complex matrix was obtained. By the method of mathematical analysis, we found the condition that this complex matrix is nilpotent. Finally, we verify that the ray patterns and all superpatterns are spectrally arbitrary by Nilpotent-Jacobian method.

Nilpotent-Jacobian method; ray pattern; spectrally arbitrary pattern; potentially nilpotent

2016-08-23

国家自然科学基金资助项目(11071227)； 山西省回国留学人员科研资助项目(12-070)

霍英杰(1991-)， 男， 硕士生， 主要从事组合数学的研究.

邵燕灵(1963-)， 女， 教授， 博士， 博士生导师， 主要从事组合数学的研究.

1673-3193(2017)02-0114-05

O157.5

A

10.3969/j.issn.1673-3193.2017.02.004