运用SOLO分类理论指导初中几何的教学

何敏霞+李雪迎

湛江一中培才学校

SOLO分类理论把学生对某个问题的学习结果由低到高划分为五个层次。运用SOLO分类理论指导教学，通过分析学生的回答，能够判断学生达到所的思维层次。笔者以《三角形全等的判定（HL）》为例，借助SOLO研究采用的教学模型进行教学设计，从教学目标和重难点的设计、学生预习效果的分析、课本例题的分析和变式等主要方面，关注学生思维水平的发展，让教师在教学中把握教学方向，调整教学过程。

一、SOLO分类理论的主要内容

SOLO分类评价理论是教育评价发展到建构主义阶段后，由澳大利亚教育心理学教授比格斯（Biggs）与其同事克莱斯（Collis）在汲取皮亚杰认知发展理论合理成分的基础上所开发的一种以等级描述为特征的“质性”评价方法。SOLO的评价是基于这样一种理念：任何学习结果的数量和质量都是由学习过程中的教学程序和学生的特点决定的。它根据学生的已有知识结构、学习的投入及学习策略等多方面的特征，从具体到抽象，从单维到多维，从组织的无序到有序。

根据SOLO分类评价法，比格斯把学生对某个问题的学习结果由低到高划分为五个层次：前结构、单点结构、多点结构、关联结构和抽象拓展结构，具体含义如下：第一，前结构层次（prestructural）：学生基本上无法理解问题和解决问题，只提供了一些逻辑混乱、没有论据支撑的答案第二，单点结构层次（unistructural）：学生找到了一个解决问题的思路，但却就此收敛，单凭一点论据就跳到答案上去。第三，多点结构层次（multistructural）：學生找到了多个解决问题的思路，但却未能把这些思路有机地整合起来。第四，关联结构层次（relational）：学生找到了多个解决问题的思路，并且能够把这些思路结合起来思考。第五，抽象拓展层次（extended abstract）：学生能够对问题进行抽象的概括，从理论的高度来分析问题，而且能够深化问题，使问题本身的意义得到拓展。从上述分类法中我们首先可以看到，比格斯提出的思维分类结构是一个由简单到复杂的层次类型，具体说来就是从点、线、面、立体、系统的发展过程，思维结构越复杂，思维能力的层次也就越高。其次，SOLO分类的焦点集中在学生回答问题的“质”，而不是回答问题的“量”。虽然没有量的支撑，质是无从体现的，但针对“质”的评价与针对“量”的评价的确大有区别。SOLO评价不在乎学生答对了多少个与标准答案相近的字眼，更不在乎学生写出了多少字，只是力求从学生的回答中分析出他能够达到哪一思维层次。

二、运用SOLO分类理论指导教学目标和重难点的设定

制订教学目标是课堂教学的第一步，是教师完成教学任务所达到的要求和标准，同时也起到指导教师课堂教学活动的作用。《三角形全等的判定（HL）》是在学习了一般三角形全等的判定的基础上，对直角三角形全等的判定进一步深入和拓展。学生已经学习了“SSS”“SAS”“ASA”“AAS”等三角形全等的判定定理，而三角形全等的判定方法“HL”这一定理只需已知一条直角边和一条斜边就可以判断两个三角形全等，这就是直角三角形所特有的性质，需要和学生前面已有的知识进行区别，而通过全等三角形的性质，可以证明对应边、对应角相等。这就是本节课需要学生达到的关联知识结构水平。因此本节课的教学目标设定为：知识与能力目标：一是探索并掌握判定直角三角形全等的‘斜边、直角边定理；二是能运用“斜边、直角边”证明两个直角三角形全等，并得到对应边、对应角相等。

教学重点的设定可以让教师在教学中把握教学方向，教学难点的设定可以指导教师在教学中突破难点。本节课都是围绕着三角形全等的“HL”的判别方法的理解和应用进行的，需要学生把“HL”定理以及全等三角形的性质进行关联，因此本节课的教学重点设定为：“斜边、直角边”判定方法的掌握和灵活运用；由于判定两个直角三角形全等不只“HL”这一定理，前面所学习的一般三角形的判定定理都适用，需要学生进行达到关联结构的水平，因此本节课的教学难点设定为：灵活选择适当的判定方法来证明两个直角三角形全等。

三、运用SOLO分类理论分析学生预习效果

通过学生的预习作业的反馈，可以让教师及时了解学生对所学知识的掌握情况，及时调整课堂教学。

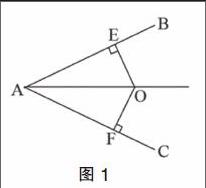
例如，在预习后设计了练习：已知在如图1中，O是∠BAC内一点，且点O到AB、AC的距离OE=OF，则判定△AEO≌△AFO的依据是 。

根据统计，全班53人，本题中有35人写了“HL”，处于关联结构水平，有12人的答案是“SSA”“SAS”或者是“ASA”“AAS”等答案，处于单点结构，而有6人没有作答，属于前结构水平。因此教学中教师需要教会学生分析已知条件和每个定理所适用的情况，从而帮助单点知识结构水平和前结构水平的学生进行提升。

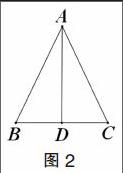
再如：如图2所示，完成下面的证明过程： AD⊥BC，AB=AC，求证：BD=CD。证明：∵ AD⊥BC∴∠__=∠__=90°；在__和__中，__=__；__=__ ∴__≌__（ ）∴BD=CD。

在本题中，有2个学生无法作答，属于前结构水平，有8名学生只能填前两个空，属于单点知识结构水平，有30名学生能写出完整过程，属于关联结构水平，而有13名学生对判定全等的条件描述错误，属于多点知识结构水平。因此在教学过程中，需要指导学生如何分析题目，把需要证明的结论和所给的条件关联起来。

而在导学案的最后，还设计有“我的疑惑”环节。教师能够从学生所提出的问题判断学生所处的思维水平。我们发现了一些非常有价值的提问，有学生提问：“为什么直角边和斜边对应相等的两个直角三角形全等？”这个问题说明此学生处于单点知识结构水平，知道“HL”定理，却不明白这个定理的由来。因此在教学中设计了学生动手操作环节，通过小组合作，把已经剪好的斜边为35cm，一条直角边为28cm的直角三角形与同组学生进行对比，让学生感受一条直角边和一条斜边对应相等的两个直角三角形全等。也有学生提问：“‘HL定理不就是前面说的‘SSA吗？”学生能够提出这个问题，说明该生处在了抽象拓展结构水平，因为此前学习“SAS”时，有提到“SSA”不一定成立的，而本节课的“HL”定理正是它成立的特殊情况，也是说在直角三角形中“SSA”成立的，其他普通三角形是不成立的，也是我们特别研究直角三角形的判定的必要性。在教学中，教师可在讲完“HL”定理后提出这个问题让学生思考，从而帮助学生知识形成系统。也是突破学生知识易错点和混淆点的关键。还有学生提问：“证明两个直角三角形全等是否只能用‘HL定理？”该学生处于多点知识结构水平，他还不能很好地将前面所学的一般三角形全等的判定和“HL”定理很好的关联在一起，即特殊图形和一般图形性质、判定的关联。因此在教学中需要点拨学生所学的所有定理都适用于直角三角形，而“HL”定理只在直角三角形中适用。

四、运用SOLO分类理论对例题进行分析和变式

例题学习是数学教学中重要的一个环节，一道好的例题具有基础性、指导性、典型性、拓展性、能最大限度发挥它的引领和辐射作用，能真正让学生掌握基础，举一反三，形成知识网络，要努力将例题的内隐部分挖掘，从不同的方向找到切入效果，达到更好的教学效果。

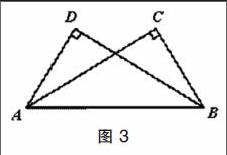
本节课课本例题如下：所如图3所示，AC⊥BC，BD⊥AD，垂足分别为C，D，AC=BD.求证：BC=AD。

这个例题中，学生容易从题目给定的“AC=BD”得到一边对应相等这个单点知识结构，通过“AC⊥BC”“BD⊥AD”得到这是两个直角三角形，形成多点知识结构。教师需要引导学生要将题目的问题和条件联系起来建立关联结构，可以设计这样两个问题：（1）要证明BC=AD，可以通过证明哪两个三角形全等？（2）要证明这两个三角形全等已知哪些条件，图形中是否有隐藏条件？从而建立起问题和条件的桥梁，让学生从多点结构思维水平发展到关联结构水平。为了拓展学生思维，将前面所学知识系统化，发展学生的抽象拓展结构水平，可以将此题进行变式训练：“若AC、BD相交于点O，图中还有哪些三角形全等？为什么？”学生可以通过“ASA”或者“AAS”证明三角形AOD和三角形BOC全等，从而对直角三角形全等的判定进行总结。

五、运用思维导图提升学生的逻辑思维

思维导图能够为学生提供思考框架，其知识表征方式及过程对知识的表达与理解，与数学教学有共通之处，在数学教学中引入思维导图，发挥思维导图在的作用可以帮助学生建构完整有效的知识网络，提升逻辑思维能力。学生学习了本节课后，大部分学生对“HL”定理可以达到关联结构水平，而为了让学生能够将前后知识进行联系，形成知识系统，让学生能够对问题进行抽象的概括，使学生能够达到抽象拓展层次。我们可以借助知识结构图将全等三角形的判定和性质进行梳理和概括。

注：本论文是广东省教育科研“十二五”规划2013年度研究一般项目（批准号2013YQJK246）课题成果之一。

责任编辑 黄博彦