基于灵敏度分析的地方性电厂出力重新分配

田 军，逯晓君，白乙童，张 师

(1.吉林电子信息职业技术学院电气工程学院，吉林 吉林 132021；2.青海黄河上游水电开发有限责任公司，青海 西宁 810000；3.吉林供电公司昌邑分公司，吉林 吉林 132000；4.东北电力大学电气工程学院，吉林 吉林 132012)

基于灵敏度分析的地方性电厂出力重新分配

田 军1，逯晓君2，白乙童3，张 师4

(1.吉林电子信息职业技术学院电气工程学院，吉林 吉林 132021；2.青海黄河上游水电开发有限责任公司，青海 西宁 810000；3.吉林供电公司昌邑分公司，吉林 吉林 132000；4.东北电力大学电气工程学院，吉林 吉林 132012)

现有的高压配电网规划方法计算量较大，只适用离线分析而不能应用于在线计算；而随着系统工况变化，高压配网的经济性和稳定性仍有较大的改进空间。为提高高压配电网规划计算速度，使其能够适用于实际系统的在线计算，基于灵敏度分析提出地方性电厂出力分配方案，并通过某实际系统验证所提出方法的有效性。通过分析可知，合理调节各地方性电厂的出力分配可有效减小系统网损指标、电压偏移指标及电压稳定L指标，提高高压配电网的电压稳定性、电能质量及经济性。

有功出力；无功出力；灵敏度分析；网损；电压偏移；电压稳定

0 引言

高压配电网是连接输电网和中压配电网的重要环节，全国80%以上的电量要经高压配电网输送给用户，因此，高压配网的经济性和可靠性研究是一项有意义的工作[1]。

目前已有的研究主要集中在高压配电网规划方面[2-8]，包括高压配电网运行评价指标的研究[2-4]、高压配电变电站选址定容[5]、高压配网全寿命周期管理成本优化[6]、提高高压配网供电可靠性的规划研究[7]、高压配电网保护配置的优化方案[8]。虽然高压配网方面已经积累了丰富的研究成果，但仍有较大的改进余地；由于电网结构复杂、计算量大[9]，对于多变的电网运行方式往往不能及时给出准确的计算结果，依靠经验的成分较大。

灵敏度理论在电力系统中已得到了广泛的应用，如：电力系统模型参数辨识[10-12]、电力系统稳定性评估[13]、电力系统谐波抑制[14]、电力系统状态估计[15]等。目前，灵敏度分析在调度发电计划中并未得到应用，而高压配网中地方性电厂的出力变化必然影响电网潮流，从而影响网络的可靠性和经济性。

基于以上分析，本文首先研究配网中地方性电厂出力对电网经济性和电压稳定性的影响；并将灵敏度理论用于对高压配网运行效率的分析中，提出提高高压配网运行经济性和电压稳定性的方法。

1 地方性电厂出力对高压配电网的影响

1.1 电压偏移分析

n个节点的配电网系统电压偏移指标可表示为[16]

(1)

式中：Ui为第i节点的电压幅值；Ui0为第i节点的电压额定值。

各节点注入功率和各节点电压的关系可表示为[17]

(2)

式中：Pi、Qi为i节点注入的有功功率、无功功率；Gij、Bij、θij分别为i、j节点间电导、电纳、相角差。

根据式(2)，将各节点注入有功功率与各节点电压的关系表示为

(3)

其中矩阵A中的各元素为

(4)

将式(3)整理得

(5)

其中矩阵B中第i行第j列的元素为

(6)

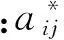
将式(5)代入式(1)，可以得出电压偏移指标与各节点注入有功功率的关系：

(7)

根据式(2)，将各节点注入有功功率与各节点电压的关系表示为

(8)

其中矩阵C中的各元素为

(9)

整理式(9)得

(10)

其中矩阵D中第i行第j列的元素为

(11)

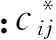
将式(10)代入式(1)，可以得出电压偏移指标与各节点注入无功功率的关系：

(12)

从以上分析可看出，无论单独调节各节点有功功率还是无功功率都会影响系统的电压偏移指标，且各节点注入功率与电压偏移指标之间为非线性关系。因此，高阶系统中求得电压偏移指标最小下各节点有功无功输出的计算量很大。

1.2 有功网损分析

n个节点的配电网系统总有功网损可表示为

(13)

式中Pij、Qij和Rij分别为第i、j节点间直接相连支路的首端有功功率、首端无功功率和支路电阻。

将式(5)、(6)分别代入式(13)，可以得出

(14)

(15)

此外，各节点注入有功、无功功率的变化还会影响各支路的功率Pij、Qij。

由以上分析可知，各节点注入的有功、无功功率与电压偏移指标之间也是复杂的非线性关系。在实际系统运行中，通过计算各节点注入的功率来优化系统网损指标的计算量很大。

1.3 电压稳定分析

电压稳定指标为

(16)

将式(5)、(6)分别代入式(16)，可以得出各节点注入功率和电压稳定指标的关系：

(17)

(18)

从式(17)、(18)可看出各节点注入的功率与电压稳定指标之间仍然是一种复杂的非线性关系，实际电力系统中优化电压稳定指标仍需较大的计算量。

2 灵敏度理论在分配各节点注入功率中的应用

2.1 采用灵敏度分析的必要性

由上文分析可知，各节点注入功率与系统的电压偏移指标、网损指标、电压稳定指标均存在非线性关系。在实际系统中，随着负荷波动及系统工况的变化，最优指标下的各节点注入功率必然是不断变化的。如果采用智能算法对大电网的各指标求最优值不仅计算量较大，且计算结果更多取决于惯性权重的设置。如果直接将各指标对各节点注入功率求导，得出各节点注入功率与各指标间关系后再进行控制仍然有很大的计算量。

2.2 灵敏度分析

灵敏度能反映任意时刻参数变化对系统状态变量的影响程度[18]，已知系统各支路参数及当前时段的潮流，采用摄动法获得的灵敏度，就可以反映每个节点当前工况下注入功率变化对各指标的影响：

(19)

(20)

(21)

(22)

(23)

(24)

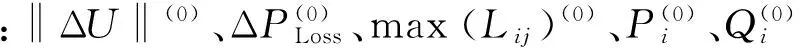
3 地方性发电厂出力重新分配方法

根据以上分析，通过计算各指标对注入功率的灵敏度，可选出对系统影响最大的发电厂，从而调节各电厂有功、无功功率，改善系统的经济性和稳定性。具体步骤如下：

1) 计算系统当前工况下潮流，求出电压偏移指标、有功网损指标、电压稳定指标，确定可调节出力的发电厂。

2) 通过逐个摄动每台发电厂出力，分别求出各指标对各发电厂有功、无功功率的灵敏度。

3) 求得对有功网损指标灵敏度最大的发电厂出力，判断其他指标对该出力的灵敏度是否与有功网损指标灵敏度同号。

4) 如果同号，调节该厂出力；如果不同号，重复步骤3)。

5) 调节有功网损灵敏度最小的电厂有功、无功出力，以平衡系统功率。

在调节电厂出力以减小系统网损的同时，该厂出力的改变可能会恶化电压偏移指标和电压稳定性指标。因此，本文通过判断各指标对电厂出力的灵敏度是否同号，在提高系统经济性的同时不会降低电压稳定性。

4 算例分析

图1 吉林某地区66 kV系统图Fig.1 66 kV system in a area in Jilin

如图1所示，本文采用吉林市某地区66 kV配电网系统，验证本文方法的有效性。系统中吉林厂有功出力40 MW；动力厂有功出力50 MW；东关厂有功出力45 MW；系统中总有功负荷为132.3 MW，无功负荷35.4 Mvar；维昌变平衡系统功率，基准功率为100 MV·A。

该系统工况下各发电厂有功出力变化对网损指标的影响如图2所示。可看出，各电厂出力变化与系统网损均为非线性关系，若要在不同系统工况下减小系统网损，调整出力的方案必然不同。

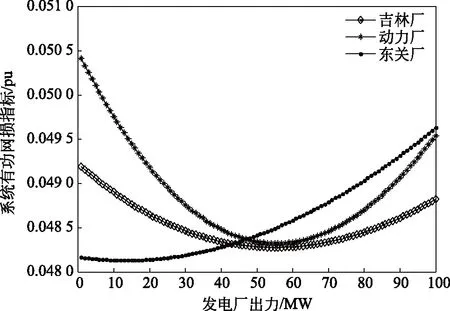
图2 不同厂有功出力变化对系统有功网损的影响Fig.2 Active power loss according to active power of different power plant

按照本文方法，首先计算该工况下电压偏移、有功网损、电压稳定对各电厂出力的灵敏度，再根据灵敏度对各电厂出力进行重新分配。

各指标对各发电厂有功、无功出力的灵敏度如表1、2所示。从表1可看出：减小东关厂有功出力可以减小网损，提高电压稳定性，减小电压偏移；动力厂对网损灵敏度最低，且对电压稳定性、电压偏移几乎无影响，因此通过减小东关厂有功出力来提高系统运行经济性，通过增加动力厂有功出力来平衡系统有功功率。从表2可看出：增发东关厂无功功率可同时提高系统的经济性和电压稳定性；而增发吉林厂和动力厂无功功率在降低电压偏移程度的同时，会恶化系统电压稳定性，增大系统网损。调整前后的各电厂出力及系统指标如表3所示。

表1 各指标对电厂有功功率的灵敏度Table 1 Sensitivity of each index to active power of power plant

表2 各指标对电厂无功功率灵敏度Table 2 Sensitivity of each index to reactive power of power plant

吉林厂、动力厂、东关厂在潮流计算中均考虑为PV节点，通过提高东关厂的机端电压即可提高东关厂的无功出力，将东关厂电压从1.0 pu提高到1.01 pu，东关厂无功出力由原来的-0.210 5 pu升为-0.045 4 pu。由于东关厂无功出力增加，提高了系统电压水平，因此吉林厂、动力厂为维持原有机端电压所需的无功出力会有所降低。

根据本文的方法可看出，调整各厂出力后，系统的电压偏移指标、网损指标和电压稳定L指标均降低了。

5 结论

本文基于灵敏度分析提出了地区性电厂有功无功出力重新分配的计算方法，可以提高高压配电网的电压稳定性和运行经济性，减小电压偏移。本文的方法相比于其他方法计算量小，仅需要计算每一时刻的灵敏度即可调节各电厂出力，可优化系统指标，并应用于在线计算分析。最后，某实际系统算例验证了本文方法的有效性。

[1] 沈瑜， 徐逸清， 陈龙翔. 高压配电网优化规划的研究[J].电网技术， 2011， 35(10)： 70-75. SHEN Yu， XU Yiqing， CHEN Longxiang. Studies on optimal planning of high voltage distribution network[J]. Power System Technology， 2011， 35(10)： 70-75.

[2] 羌丁建， 寿挺， 朱铁铭， 等. 高压配电网规划评价指标体系与综合评价模型[J]. 电力系统保护与控制， 2013， 41(21)： 53-57. QIANG Dingjian， SHOU Ting， ZHU Tieming， et al. An evaluation index system and comprehensive evaluation model on high-voltage distribution network planning[J]. Power System Protection and Control， 2013， 41(21)： 53-57.

[3] 芦晶晶， 赵渊， 赵勇帅， 等. 含分布式电源配电网可靠性评估的点估计法[J]. 电网技术， 2013， 37(8)： 2250-2257. LU Jingjing， ZHAO Yuan， ZHAO Yongshuai， et al. A point estimation method for reliability evaluation of distribution network with distributed generation[J]. Power System Technology， 2013， 37(8)： 2250-2257.

[4] 李志铿， 汪隆君， 王钢， 等. 计及故障重构的含分布式电源配电网可靠性评估[J]. 电力系统自动化， 2013， 37(4)： 35-40. LI Zhikeng， WANG Longjun， WANG Gang， et al. Reliability evaluation for distribution system with distributed generations considering reconfiguration[J]. Automation of Electric Power Systems， 2013， 37(4)： 35-40.

[5] 侯勇. 高压配电网规划中变电站选址定容与协调优化问题研究[D]. 北京： 华北电力大学， 2006.

[6] 刘大利. 迁安市高压配电网规划研究[D]. 保定： 华北电力大学， 2014.

[7] 曾嘉思， 徐习东， 赵宇明. 交直流配电网可靠性对比[J]. 电网技术， 2014， 38(9)： 2582-2589. ZENG Jiasi， XU Xidong， ZHAO Yuming. Reliability comparison of AC and DC distribution network[J]. Power System Technology， 2014， 38(9)： 2582-2589.

[8] 尚瑨， 邰能灵， 刘琦， 等. 考虑分布式电源的配电网保护改进方案研究综述[J]. 电力系统保护与控制， 2012， 40(24)： 40-46. SHANG Jin， TAI Nengling， LIU Qi， et al. New protection method for distribution network with DG[J]. Power System Protection and Control， 2012， 40(24)： 40-46.

[9] 李鹏. 基于群搜索优化算法的配电网重构[D]. 长沙： 湖南大学， 2011.

[10] 安军， 王孜航， 穆钢， 等. 基于WAMS测量和戴维南等值的电力系统动态仿真误差溯源及可信度验证方法[J]. 电网技术， 2013， 37(5): 1389-1394. AN Jun, WANG Zihang, MU Gang, et al. Confidence level verification and tracking to error source for power grid dynamic simulation based on WAMS and Thevenin equivalence[J]. Power System Technology, 2013， 37(5): 1389-1394.

表3 调整前后各电厂出力及系统指标Table 3 Power output and system index before and after adjustment

[11] 刘洪波. 基于量测轨迹及轨迹灵敏度的电力系统动态分析[D]. 保定： 华北电力大学， 2007.

[12] 马进， 王景钢， 贺仁睦. 电力系统动态仿真的灵敏度分析[J]. 电力系统自动化， 2005， 29(17)： 20-27. MA Jin， WANG Jinggang， HE Renmu. Sensitive analysis of power system dynamic simulation[J]. Automation of Electric Power Systems， 2005， 29(17)： 20-27.

[13] 邹建林， 安军， 穆钢， 等. 基于轨迹灵敏度的电力系统暂态稳定性定量评估[J]. 电网技术， 2014， 38(3)： 694-699. ZOU Jianlin， AN Jun， MU Gang， et al. Quantitative assessment of the transient stability of power system based on trajectory sensitivity[J]. Power System Technology， 2014， 38(3)： 694-699.

[14] 仰彩霞. 基于模态分析法的电力系统谐波谐振问题研究及灵敏度分析[D]. 武汉： 武汉大学， 2010.

[15] 王永， 郭志忠， 彭茂君， 等. 基于灵敏度分析的多区域互联电力系统状态估计[J]. 电力系统自动化， 2007， 31(19)： 27-31. WANG Yong， GUO Zhizhong， PENG Maojun， et al. State estimation of a multi-area interconnected power system based on sensitivity analysis[J]. Automation of Electric Power Systems， 2007， 31(19)： 27-31.

[16] 曾颖. 电网运行效率评价方法与应用[D]. 广州： 广东工业大学， 2015.

[17] 陈珩. 电力系统稳态分析[M]. 北京： 中国电力出版社， 2007.

[18] 张梦雅. 基于轨迹灵敏度的电力系统预防控制研究[D]. 吉林： 东北电力大学， 2015.

田 军

(编辑 谷子)

Local Power Plant Output Re-Distribution Based on Sensitivity Analysis

TIAN Jun1, LU Xiaojun2, BAI Yitong3, ZHANG Shi4

(1. Institute of Electrical Engineering, Jilin Technology College of Electronic Information, Jilin 132021, Jilin Province, China;2. Qinghai Yellow River Upstream Hydro Power Development Co.， Ltd., Xining 810000, Qinghai Province, China;3. Changyi Branch of Jilin Power Supply Company, Jilin 132000, Jilin Province, China;4. Institute of Electrical Engineering, Northeast Dianli University, Jilin 132012, Jilin Province, China)

The computational complexity of existing planning method for HV distribution network is big, which is only for off-line analysis and can not be applied to online calculation. With the change of system operating condition, the economy and stability of HV distribution network still have great improvement space. In order to improve the calculation speed of HV distribution network planning, and make it can be applied to on-line calculation of actual system, this paper presents the local power plant output redistribution scheme based on the sensitivity analysis, and verifies the effectiveness of the proposed method by a practical system. According to this analysis, it shows that the reasonable adjustment of the local power plant output distribution can effectively reduce the network loss index, voltage deviation and voltage stabilityLindex, and improve the voltage stability, power quality and economy of HV distribution network.

active power output; reactive power output; sensitivity analysis; power loss; voltage deviation; voltage stability

TK 01;TM 71

A

2096-2185(2017)03-0050-06

10.16513/j.cnki.10-1427/tk.2017.03.009

吉林省教育厅“十三五”科学技术研究项目(2016107)

2017-03-03

田 军(1982—)，男，硕士，讲师，研究方向为电力系统动态安全分析，15338233@qq.com;

逯晓君(1989—)，男，学士，助理工程师，研究方向为电力系统规划，deadmcover@qq.com;

白乙童(1989—)，女，学士，助理工程师，研究方向为电力系统规划，76910672@qq.com;

张 师(1989—)，男，硕士，助理实验师，研究方向为电力系统动态安全分析，zs472254835@126.com。