导流隔板式相变储热单元性能强化的模拟

马 林

(中国大唐集团科学技术研究院有限公司火力发电技术研究所，北京 石景山 100040)

导流隔板式相变储热单元性能强化的模拟

马 林

(中国大唐集团科学技术研究院有限公司火力发电技术研究所，北京 石景山 100040)

传统相变储热单元采用简单内外套管结构，其换热性能因相变过程中固-液界面分布不均匀而受到限制，为此提出了水平隔板式与倾斜导流隔板式这2种新型套管。建立了3种套管的数学及物理模型，对其相变过程进行了二维非稳态模拟计算，比较了这3种结构换热性能的差别，并对影响导流隔板换热性能的因素作了分析。与传统结构相比，水平隔板使相变材料(phase change material, PCM)融化时间缩短了40.2%，倾斜隔板使融化时间缩短了65%。结果表明，导流隔板有效削弱了PCM融化过程中的固-液界面分布不均匀现象，有效缩短了PCM融化时间，并且通过调整隔板数量及倾斜角度可进一步提高套管换热性能。

导流隔板；相变材料；储热单元；套管

0 引言

目前，分布式能源发电技术是国际能源技术发展的热点，在优化能源结构、促进节能减排、改善能源环境问题等方面将发挥重要作用[1]。以可再生能源为供能基础的分布式能源发电系统具有能量供给的波动性与随机性等特点，导致能量的产生与消费不能实现实时的供给平衡，而分布式储能技术可有效消除能量的时空随机性，提高供能系统的稳定性[2-3]。

相变材料(phase change material, PCM)因其储热量大、成本低等优点正成为储能技术领域的研究热点。但由于PCM在换热过程中存在固-液界面不均匀现象，导致相变储热单元换热时间长。因此增强相变储热单元换热性能，缩短相变时间是研究的重点工作之一[4]。

目前，改善相变材料换热性能，削弱固-液界面不均匀现象的主要方式包括增加导热面积、构建复合材料、加入高导热性材料等措施。吴斌等人对充填高导热性多孔筛网的套管式储热单元建立了二维的数学及物理模型，并进行了相变蓄热试验，试验表明，增加筛网可以有效提高储热单元的传热性能[5]。廖百胜利用CFX软件，对于不同内径的套管换热器，在不同偏心距情况下进行了数值模拟计算。计算结果表明，在套管内流体湍流程度中等时，伴随着偏心距的增大，粘滞力影响逐渐增大，导致换热器内的传热效果恶化，恶化情况最为严重的是当内、外壁面相互接触时的工况条件[6]。杨佳霖等人将泡沫金属铜加入到相变材料中，通过利用泡沫金属铜的高导热性与比表面积来提高石蜡换热性能，结果表明，泡沫金属使储热单元内温度分布更加均匀，融化时间明显缩短[7]。徐明以聚乙糖醇作为蓄热材料，针对具有内环肋与翅片结构的换热器进行了优化设计，并由此得出最优管长的计算结果[8]。贺鹏通过模拟计算，对光管相变储热单元、横纹槽管相变储热单元、翅片管相变储热单元及横纹槽翅片管储热单元做了换热性能比较，结果表明，横纹槽翅片结构对于增强换热效果作用更加明显[9]。陈佳等人提出了一种带有赤藓糖醇材料的翅片缩放管式储热单元，结果表明，翅片缩放管在储热过程中的传热速率分别比光管缩放管快13%和9%，适当增大翅片厚度有利于提高蓄热体的换热性能[10]。

本文在考虑自然对流的情况下，以石蜡为相变材料，通过在套管内增加导流隔板的方式改善套管储热单元换热性能，对3种不同结构的相变储能单元的换热过程进行了数值研究，并进一步研究了导流隔板数量及倾斜角度对换热性能的影响。

1 数学模型及物理模型

1.1 数学模型

套管模型分为2个区域: 管内湍流区域和石蜡相变区域。数值模拟主要分析石蜡相变区域的融化相变过程。因为融化过程中固液相变界面不断移动，使得此类相变问题很难得到精确解。本文利用热焓-多孔技术，把相变区域作为一个整体来看待，无需跟踪界面的变化情况，同时把固液两相的共存的区域当成多孔介质区，按多孔介质处理。采用α表示液相率，当α=0时，表示相变材料全部凝固，当α=1时，表示相变材料全部熔化[11]。PCM控制方程[12]如下所示。

连续方程：

(1)

式中：ρ为PCM的密度，kg/m2；u、v分别为PCM沿x、y方向液相速度矢量，m/s。

动量方程：

(2)

(3)

(4)

式中：β为PCM的孔隙率；S为源项，Su、Sv为分别为S在u、v上的分量；ε为小于0.001的数，避免分母等于0；Amush为模糊区常数，常取值为104～107，为阻尼振幅尺度的量度，该值太大会引起结果震荡[13]。

(5)

式中：ρref为参考密度，kg/m3；tref为参考温度，。

能量方程：

(6)

(7)

(8)

(9)

(10)

式中：H为PCM总焓值，kJ/kg；cp为定压比热容，J/(kg·K)；L为相变潜热，J/kg；k为导热系数；h为显热焓值，kJ/kg；href为参考温度下的参考焓值，kJ/kg；T为绝对温度，K；Tref为参考温度，K。

PCM控制方程必须满足如下假设条件：

(1) PCM溶解热、体积膨胀系数为常数，固-液两相密度、定压比热、导热系数不同。

(2) PCM纯净，且各向同性。

(3) 相变过程发生在一个温度区间内，焓与温度的关系认为是线性的。

(4) 满足Boussinesq假设，只在浮力项中考虑密度变化，认为流体密度与温度的关系是线性的[14]。

(5) 假设套管内壁面热阻为0，外壁面与外界环境绝热。

1.2 物理模型

普通套管模型高10 cm，内管直径1 cm,外观直径5 cm结构如图 1(a)所示；在普通套管模型的内外管之间平均增加3层横向隔板，间距2.5 cm,结构如图 1(b)所示；将横向隔板改为倾斜隔板，倾斜高度为2.5 cm与水平隔板位置对应，结构如图 1(c)所示。加热工质(水)通过内管向储热单元传递热量，上端口进入，下端口流出。内管与外管之间储热石蜡，热量通过内管壁面传递给石蜡。

图1 套管结构示意图Fig.1 Structure of casings

边界条件和初始条件为：

(1) 内管热流体为液态水，流速0.5 m/s，温度300 K。

(2) 内外管之间PCM为石蜡，初始温度288 K，物性参数见表1。

(3) 套管竖直放置，重力沿套管竖直向下。

表1 石蜡物性参数Table 1 Material properties of paraffin

2 数值计算结果及分析

由于对称性，取套管纵切面的一半作为计算模型，采用Gambit建立物理模型并用结构与非结构四边形形式划分网格。Fluent采用2D分离、隐式、非稳态求解器求解；能量方程、动量方程采用二阶迎风差格式，离散项中压力梯度采用PRESTO，松弛因子的选择采用0.1。

2.1 液相率云图

图2为1种模型在不同时刻的液相率云图，刻度1对应完全液体状态，刻度0对应完全固体状态。

图2 液相率云图Fig.2 Contours of liquid fraction

从图 2(a)中看出，在融化开始阶段热传导为主要传热方式，在内管壁外侧率先开始出现融化的石蜡，随着融化的石蜡开始增加，自然对流在石蜡内部开始发挥作用，在重力和浮生力作用下，率先融化的石蜡汇集于导管顶部，形成锥形融化结构，这种结构不利于将热量继续传递到底部的石蜡，导致底部石蜡融化缓慢，增加了整个相变过程的时间。从图2(b)可以看出，加入隔板以后，在每个隔板下部都会出现锥形的融化趋势，明显改善了换热情况。从图2(c)可以看出，随着融化过程继续进行，在石蜡融化中后期，倾斜导流隔板模型中石蜡融化效果更加均匀，而水平隔板模型中受热不均问题开始阻碍融化过程。从图2(d)可以看出，倾斜导流隔板模型在石蜡接近完全融化前仍然受热较为均匀。

2.2 温度云图

图3 温度云图Fig.3 Contours of temperature

3种模型温度云图如图 3所示，从图 3(a)可以看出,在整个熔化过程中，热量始终集中在套管顶部，在顶部石蜡融化为液体后，开始出现不规则的热量分布，严重影响石蜡均匀受热熔化。从图 3(b)可以看出，加入水平导流隔板后，热量分布较为均匀，每层隔板顶部热量可以加热上一层石蜡的底部，加快了每一层底部石蜡的融化速率，从而缩短了整体相变时间。从图3(c)可以看出，加入斜板后，石蜡受热极为均匀，在融化后期，整个石蜡内部温度接近一致，大大减小了石蜡相变时间。

2.3 完全融化时间

图4为3种套管液相率随时间变化表。模型a完全融化时间为3 115 s；模型b完全融化时间为1 863 s，时间缩短40.2%；模型c完全融化时间为1 089 s，时间缩短65%。可见模型c能够大幅提高套管换热性能，缩短储热时间。

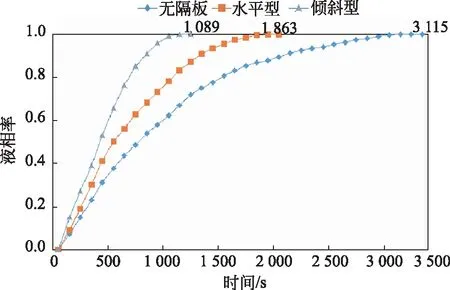
图4 液相率随时间的变化曲线Fig.4 Curves of liquid fraction changing with time

2.4 隔板间距对换热性能的影响

如图5所示，其他条件一定时，套管换热性能随隔板间距变化规律如所示，换热性能随隔板间距减小而提高。

图5 液相率随隔板间距的变化曲线Fig.5 Curves of liquid fraction changing with space between partitions

图6 液相率随隔板倾斜角度的变化曲线Fig.6 Curves of liquid fraction changing with degree of partitions

2.5 隔板倾斜角度对储热性能的影响

其他条件一定时，套管换热性能随隔板倾斜角度变化规律如图6所示。

2.6 模型验证

为了验证数学模型及计算方法的正确性，以文献[9]的实验装置作为物理模型，采取与文献中相同的初始条件及边界条件，热流体进口温度为358 K，流量为100 L/h。图 7给出了文献[15]实验装置中2号温度测点与数值模拟中相应点的温度对照关系，可以看出实验结果与模拟结果基本相同。

图7 理论与实验对应点温度对照关系Fig.7 Corresponding relationship of temperature of certain points between theory and experiment

3 结论

本文建立了考虑自然对流情况下的套管二维计算模型，提出了水平导流隔板、倾斜导流隔板2种新型相变储热单元结构，对比了3种储热单元的储热换热性能。

(1) 相变储热单元增加导流隔板后，固-液界面分布不均匀现象明显被削弱，相变储热单元的换热性能大幅提升，相变材料融化时间大幅缩短。

(2) 倾斜式导流隔板比较于水平隔板，解决了底部边缘位置相变材料受热不均的问题，温度分布更加均匀一致。

(3) 在一定范围内，减小隔板间距及调整隔板倾斜角度可以进一步提高套管换热性能。

[1] 金红光， 隋军. 变革性能源利用技术——分布式能源系统[J]. 分布式能源, 2016, 1(1): 1-5. JIN Hongguang, SUI Jun. Transformational technology innovation-distributed energy system[J]. Distributed Energy, 2016, 1(1)： 1-5.

[2] 慈松， 李宏佳， 陈鑫， 等. 能源互联网重要基础支撑: 分布式储能技术的探索与实践[J]. 中国科学: 信息科学, 2014, 44(6): 762-773. CI Song, LI Hongjia, CHEN Xin, et al. The cornerstone of energy internet: Research and practice of distributed energy storage technology[J]. Science China: Information Science, 2014, 44(6): 762-773.

[3] 严俊, 赵立飞. 储能技术在分布式发电中的应用[J]. 华北电力技术, 2006, 36(10): 16-19. YAN Jun, ZHAO Lifei. Energy storage for distributed generation[J]. North China Electric Power, 2006, 36(10): 16-19.

[4] 张永信， 李舒宏， 操恺， 等. 太阳能相变储能水箱释能性能的数值模拟[J]. 储能科学与技术, 2013, 2(4): 377-382. ZHANG Yongxin, LI Shuhong, CAO Kai, et al. Numerical analysis of the discharging performance of a solar energy storage tank containing PCM modules[J]. Energy Storage Science and Technology, 2013, 2(4): 377-382.

[5] 吴斌， 邢玉明. 适用于废热回收的相变蓄热装置数值模拟与实验研究[J]. 热能动力工程, 2011, 26(1): 53-57. WU Bin, XING Yuming. Numerical simulation and experimental study of a phase change heat accumulation device applicable for waste heat recovery[J]. Journal of Engineering for Thermal Energy & Power, 2011, 26(1)： 53-57.

[6] 廖百胜. 套管式换热器结构变化对换热能力影响的模拟研究[J]. 制冷与空调, 2010, 24(1): 40-44. LIAO Baisheng. Simulation research of impact of heat exchanger capacity of heat exchanger casing’s structural changes[J]. Refrigeration and Air Conditioning, 2010, 24(1)： 40-44.

[7] 杨佳霖， 杜小泽， 杨立军， 等. 泡沫金属强化石蜡相变蓄热过程可视化实验[J]. 化工学报, 2015, 66(2): 497-503. YANG Jialin, DU Xiaoze, YANG Lijun, et al. Visualized experiment on dynamic thermal behavior of phase change material in metal foam[J]. CIESC Journal, 2015, 66(2): 497-503.

[8] 徐明. 相变蓄热换热器的数值模拟及优化设计[D]. 西安： 西安建筑科技大学， 2015. XU Ming. Numerical simulation and optimization of phase change thermal storage exchanger[D]. Xi’an： Xi’an University of Architecture and Technology, 2015.

[9] 贺鹏. 具有相变蓄热体的蓄热换热器研究[D]. 广州： 华南理工大学， 2013. HE Peng. Regenerative heat exchanger with phase change of the regenerator [D]. Guangzhou：South China University of Technology, 2013.

[10] 陈佳， 冯毅. 翅片缩放管相变蓄热体热工特性数值模拟[J]. 压力容器， 2013，30(8): 38-45. CHEN Jia， FENG Yi. Numerical simulation on thermal characteristics of fin converging-diverging channel regenerator with phase change materials[J]. Journal of Pressure Vessels, 2013, 30(8): 38-45.

[11] 王亮. 套管式蓄热器热性能数值模拟及实验研究[D]. 石家庄： 河北科技大学， 2012. WANG Liang. Numerical simulation and experimental study on thermal performance of multi tube heat storage[D]. Shijiazhuang： University Of Science and Technology Of Hebei, 2012.

[12] 邹得球， 肖睿， 宋文吉，等. 一种余热利用相变石蜡储热过程的数值模拟[J]. 热能动力工程， 2010， 25(1): 77-81. ZOU Deqiu, XIAO Rui, SONG Wenji, et al. Numerical simulation of the heat storage process of a waste heat utilization-oriented phase-change paraffin[J]. Journal of Engineering for Thermal Energy & Power, 2010, 25(1): 77-81.

[13] 韩广顺， 丁红胜， 王培伦， 等. 偏心管翅式相变储热单元性能强化的模拟[J]. 节能技术, 2015, 33(6): 483-488. HAN Guangshun, DING Hongsheng, WANG Peilun, et al. Numerical simulation on performance enhancement of eccentric fin-tube latent heat storage unit[J]. Energy Conservation Technology, 2015, 33(6): 483-488.

[14] 王哲斌, 许淑惠, 严颖. 石蜡相变蓄热过程数值模拟[J]. 北京建筑工程学院学报, 2008, 24(2): 15-18.

WANG Zhebin, XU Shuhui, YAN Ying. Simulation of the heat transfer of melting process of paraffin[J]. Journal of Beijing University of Civil Engineering and Architecture, 2008, 24(2): 15-18.

[15] 周园. 相变材料的蓄/放热性能研究[D].上海: 上海交通大学, 2009. ZHOU Yuan. The research of accumulation/release of heat phase change material[D]. Shanghai: Shanghai Jiao Tong University, 2009.

马 林

(编辑 蒋毅恒)

Numerical Simulation on Performance Enhancement of Lead-Flow Partition Phase Change Heat Storage Unit

MA Lin

(Institute of Thermal Power Generation Technology, China Datang Corporation Science and Technology Research Institute Co., Ltd., Shijingshan District, Beijing 100040, China)

The traditional heat storage unit based on phase change material (PCM) adopts the simple inner and outer casing structure of which the heat transfer performance is limited due to the uneven distribution of the solid-liquid interface. Therefor, this paper proposes two new types of horizontal and inclined lead-flow partition casings, establishes three different mathematical and physical models of casings, simulates the transition process by two dimensional unsteady state, compares the differences of heat transfer performance between these three structures and analyzes the factors affecting the heat transfer performance of the lead-flow partition. Compared with the traditional structure, the PCM melting time has been reduced by 40.2% by horizontal lead-flow partition and 65% by inclined lead-flow partition. The results show that the lead-flow partition can effectively weaken the uneven distribution of the solid-liquid interface and shorten the PCM melting time, and the heat transfer performance of the casing can be further improved by adjusting the number and inclination of partitions.

lead-flow partition; phase change material; heat storage unit; casing

TK 02

A

2096-2185(2017)03-0039-06

10.16513/j.cnki.10-1427/tk.2017.03.007

2017-05-07

马林(1991—)，男，硕士研究生，主要从事电厂节能与环保领域研究工作，Meryn@foxmail.com。