考虑低碳效益的混合能源微电网优化调度

靳现林，蔡晓宇

(1.国华能源投资有限公司，北京 东城 100007；2.华北电力大学,北京 昌平 102206)

考虑低碳效益的混合能源微电网优化调度

靳现林1，蔡晓宇2

(1.国华能源投资有限公司，北京 东城 100007；2.华北电力大学,北京 昌平 102206)

近年来，包含可再生能源发电的微电网技术得到了快速发展。针对包含多种新能源和新型负荷的微电网存在能量利用效率低的问题，研究了混合能源微电网的优化调度问题，并在优化调度模型中考虑需求侧响应和低碳效益。优化过程中，将含有光伏、风机、热电联供系统、电动汽车的微电网为研究对象，建立各电源出力模型。以包含燃料费用、运行维护费用、购售电费用、微电源折旧费用及碳处理费用的总费用最小为目标函数，在满足各类约束条件下，采用改进的萤火虫算法求解目标函数。结合算例，计算不同运行方案下微电网总运行费用，并分析各方案的低碳效益，寻求经济性和低碳效益的平衡以得到该微电网最佳运行方案。

微电网；优化调度；混合能源；低碳效益；需求侧管理

0 引言

我国北方地区风能和太阳能储量丰富，热负荷需求量也大，包含热电联供和可再生发电(风力发电，光伏发电)的微电网经济性好，实用性和可靠性高，有良好的发展前景[1-3]。随着储能设备和电动汽车的发展，推进了电网与电动汽车间的能量双向流动，这就对考虑需求侧管理(demand side management, DSM)和电动汽车(electric vehicles, EV)的微电网优化调度提出了新的要求[4-6]。

目前，针对微电网优调度问题，一般以经济性为主要考虑因素，文献[7]以微电网运行成本最小为目标函数，考虑分布式电源不确定性对经济的影响，建立了微电网动态经济调度模型。随着微电网结构的不断复杂化且环境污染问题加重，微电网优化调度中对环保成本也日渐重视，文献[8-9]建立了微电网多目标动态优化调度的一般模型，仿真模块使用能量模型对系统调度方案的经济、环境指标进行评估。在推进电采暖替代趋势下，热电联供形式由于具有高效性被应用到微电网中，文献[10]建立了含热电联供系统(combined heat and power, CHP)的微电网模型，对结合经济调度和污染治理2方面的多目标优化进行研究。文献[11]提出一种考虑热网-电网综合潮流的用户侧综合能源系统的规划方法。考虑经济、节能、环保因素，建立微型能源站二层规划模型。文献[12]建立了综合能源园区系统供给侧、需求侧和传输侧的模型，提出了一种二阶段短期优化调度策略。文献[13]在含CHP的混合能源微电网的基础上，考虑电动汽车和需求侧响应，建立以最优经济性为目标的混合能源调度模型。

本文以含有电动汽车的CHP微电网为研究对象，综合考虑CHP、需求侧响应以及电动汽车在微电网中协调运行，在目标函数中加入碳处理成本来衡量低碳效益，建立更加系统、全面的优化调度模型。采用改进的萤火虫优化算法求解目标函数，相较于基本萤火虫算法寻优性能更好，最后通过算例分析验证了该调度模型能够同时提高微电网的经济性和低碳效益，对提高微电网能量利用效率有积极的意义。

1 混合能源微电网模型

1.1 热力系统模型

1.1.1 CHP模型

微型燃气机CHP系统有2种运行模式：电负荷模式和热负荷模式。CHP系统有良好的稳定性和经济性，而且微型燃气机在电负荷模式下能很好地适应外部负荷变化。

含微型燃气机的CHP系统的数学模型如下所示：

(1)

式中：RMT(u)为u时刻燃气机提供的制热量；ηe(u)为燃气机的效率；η1燃气轮机的热损失系数；Qe(u)为u时刻燃气机输出电功率；Rhe(u)为u时刻燃气轮机烟气余热提供的制热量；Lhe为换热器的换热系数；WMT为天然气消耗量；Δu为燃气机的运行时间；M为天然气的低热值，一般取值为9.7 kW·h/m3。

1.1.2 燃气锅炉模型

天然气的消耗量取决于热负荷量Qheat-load及锅炉的热效率ηboiler。热效率是锅炉运行经济性的重要指标，体现了设备的先进程度及运行管理水平。一般地，热效率取0.88[14]。天然气消耗量Wboiler为：

(2)

1.2 可再生能源发电模型

1.2.1 光伏发电模型

光伏单元输出取决于许多变量，包括材料、温度、表面太阳辐射度，其输出功率可用下式表示：

(3)

式中：Ppv为光伏板输出功率；PSTC为标准测试条件STC下(太阳辐照度1 000 W/m2，温度为25 ℃)光伏板的最大输出功率；k为功率温度系数，可取为-0.47 %/℃；Tc为光伏板工作环境温度；Tref为参考温度，设为25 ℃；GT光照辐射度；GSTC为STC条件下光照辐射度，取为1 000 W/m2。且有：

(4)

式中：Ta为环境温度，℃；G为水平面上的光照辐射度， kW/m2；TNOT为正常运行时光伏板的温度，约为48 ℃。

1.2.2 风力发电模型

风机的输出功率取决于风机叶片面积、风速和周围空气密度。对于风机位置确定的情况，风机出力可表示为风速的函数，即：

(5)

式中：vci、vr、vco分别为风机的切入风速、额定风速及切出风速。

1.3 储能模型

本文储能系统中采用的是铅酸蓄电池。电池的荷电状态(state of charge, SOC)是反映电池可用容量的重要参数，t+Δt时刻的SOC值与t时刻的SOC值有关，电池的充放电情况如下式表示：

(6)

式中：St+Δt、St分别为t+Δt和t时刻的SOC值；Pbat-t为电池在该时间段内的充放电功率；Cbat为蓄电池容量。

蓄电池寿命有限，在充放电次数达到上限后需要更换。因此，除了电池充放电损耗，还需要考虑电池的折旧费用。另外，电池的充放电深度也会影响电池寿命。考虑电池类型，充放电过程中电池折旧费用可表示为：

(7)

电池的循环次数与放电深度的关系可表示为：

(8)

式中：N为放电深度为DN的等效循环次数；a1、a2、a3、a4分别为铅酸蓄电池特征参数，分别取值为-16.27, 2.679, 4 110，-1.85。

1.4 电动汽车模型

电动汽车具有“电源”和“负荷”双重性质，作为储能设备和大电网连接。与微电网签订需求侧管理(调度)协议的电动汽车，可作为能源管理方参与调度。

电动汽车的充电循环可表示为：

(9)

式中：Cir为充电循环；L为英里数；λec为效率系数；Ld为电动汽车日行英里数。

电动汽车充放电功率与电池特性及荷电状态有关，充放电特性与储能蓄电池相似。

1.5 需求侧响应模型

本文在分时电价策略下研究需求侧响应，根据不同的需求侧管理策略，在交互方式下，定义电负荷中的“交叉弹性需求”为可转移负荷。可转移负荷的复合模型为：

(10)

式中：i= 0, 1, 2，…，23表示1天24 h；d(i)为用户电需求；P(j)电力用户电价；A(i)为用电补贴；E(i)为交叉价格弹性。

2 优化调度模型

2.1 目标函数

在CHP混合能源系统中，系统的运行费用包括燃气费(燃气机和锅炉)、系统购售电费、充放电损耗费用(包括蓄电池和电动汽车的折旧费用)，由于天然气燃烧和大电网发电过程中会产生碳排放，因此目标函数中还包括碳处理费用。风机和光伏的运行维护费用会对运行出力略有影响，为不失一般性，在目标函数中再加入运行维护费，目标函数为：

(11)

式中：C为一个调度周期内系统总运行费用，元；Cgs和Cep分别为燃料费用和系统购售电费用；Com为分布式发电单元运行维护费用；Cso为蓄电池和电动汽车电池折旧费用；Ccb为碳处理费用。购售电费可由下式计算：

(12)

(13)

(14)

(15)

在式(14)中：Cm为发电机初始总投资；Cs和Cop分别为发电单元沉没成本和运行维护费用；γ为银行利率。式(15)中：Cstorage和Cev分别为电池折旧费用，前者计算公式见(7)。

碳处理费用为：

(16)

2.2 约束条件

电功率平衡约束为：

(17)

式中：PG(t)为分布式电源的输出；Pst(t)为储能设备的输出功率，当储能设备充电时取负值；PEV(t)为电动汽车放电功率，同样地，充电时取负值；PGrid(t)为大电网放电功率，当其从微电网吸收功率时，取负值；PD(t)为微电网电负荷功率。

热负荷平衡约束为：

(18)

式中：Qboiler(t)为锅炉发出的热功率；QMT(t)燃气机热功率；QD(t)为微电网热负荷功率。

发电设备功率上下限约束为：

(19)

式中：PGi,min、PGi,max分别为分布式电源出力PGi(t)的下限和上限。

储能荷电量及充放电功率约束为：

(20)

式中：Est,minEst,max分别为储能电荷量Est(t)的下限和上限；Pch(t)、Pch,max、Pdis(t)、Pdis,max(t)分别为储能电池的充放电瞬时功率及其上限值。电动汽车约束条件与储能设备同理，故不再详述。

3 萤火虫优化算法

萤火虫算法(firefly algorithm，FA)是一种基于生物群智能的随机优化算法，该算法通过模拟萤火虫种群因相互吸引而朝着更亮的萤火虫进行移动的特性来实现问题的优化求解。萤火虫算法与粒子群、蚁群算法相比具有计算精度高、收敛速度快的特点，目前已应用于图像处理[15]、数据挖掘[16]、通信[17]以及电力系统[18]等领域。

在FA算法中，萤火虫的移动方向和距离主要由亮度和吸引度决定，荧光度决定目标函数值，荧光亮度决定萤火虫的位置。初始时刻所有萤火虫在空间内随机分布，假设萤火虫最大的荧光亮度值为I0(r=0处荧光亮度)，最大吸引度为β0，则有如下定义。

定义1 萤火虫的相对荧光亮度

(22)

定义2 萤火虫吸引度

(23)

定义3 萤火虫i被萤火虫j吸引的位置更新公式

(24)

式中：相对荧光亮度I与目标函数值相关，目标函数值越优其自身亮度越大；γ为光吸收系数，γ介于0.01到100之间，表示随着距离增加以及传播媒介的吸收荧光亮度逐渐减弱的特性；rij表示萤火虫i与j的笛卡尔距离；α为步长因子，介于0到1之间；λrand为随机扰动项，以防止迭代过早陷入局部最优。萤火虫优化算法流程图如图1所示。

图1 基本萤火虫算法流程图Fig.1 Flow chart of basic FA

为了解决FA算法前期搜索精度差、后期搜索易陷入局部最优的问题，采用了一种基于参数方差调节的改进萤火虫算法[19](GFA)，该改进的核心思想在于根据种群迭代次数对迭代过程进行搜索初期和后期进行划分，不同的阶段采用不同的参数结构，因此就需要检验种群迭代的收敛、离散情况。本文将种群发散定义为初期迭代过程，将种群收敛定义为优化的后期迭代过程。通过计算种群萤火虫的亮度方差来衡量种群的敛散变化情况。GFA有这样的定义。

定义4 归一化算子公式

(25)

定义5 荧光亮度方差

(26)

式中n为萤火虫个数。

定义6α、β、γ更新公式

(27)

在α与γ的表达式当中，下标b表示起始，下标e表示终止；k为调节系数，以方差σI来反映萤火虫种群中收敛程度，当σI越小时说明萤火虫位置越集中，算法迭代过程越接近于收敛，参数越接近终止值；当σI越大时说明萤火虫位置越分散，参数越接近起始值。相应的位置更新公式可表示为：

(28)

(29)

式中L为亮度。在此亮度有差异的情况下人为引入参数K来提高萤火虫的吸引力，有利于快速找到较优解。

4 算例分析

本文以中国北方地区某微电网为例验证上述模型和算法的有效性，该微电网供电范围内包含1个小型工厂、市场和居民区。微电网内电负荷和热负荷最大值分别为265 kW和313 kW。微电网能量输入单元含2台C65微型燃气轮机，储能系统由60个12 V/200 A·h铅酸蓄电池串联组成，其最大充电功率、最大放电功率分别为20 kW和40 kW。微电网内含20辆电动汽车，其中10%与微电网运行方签订调度协议，其余只能充电。电动汽车充电1次可行驶250 km，效率系数取为0.67，每天行驶24.5 km，充电周期为7天。由此可得每天有2辆电动汽车参与调度，3辆作为负荷。光伏阵列最大输出功率为100 kW，风机额定输出功率为150 kW,燃气机额定功率300 kW。热负荷缺额由燃气轮机(GB)平衡。设备初始投资远大于运行费用，由于初始投资为定值，在算例场景中不再考虑初始投资。

4.1 运行模式

运行模式1： 电、热负荷分开供应热负荷由燃气锅炉独立供应，微电网的负荷优先由风机和光伏供应，余者由大电网供应。

运行模式2： 混合供能，不考虑储能、电动汽车及需求侧管理。热负荷由燃气轮机和燃气锅炉同时供应，风机和光伏只供应微电网负荷。

运行模式3： 混合供能，蓄电池参与供能，不考虑电动汽车和需求侧响应。热负荷供应同场景2，风机和光伏供给微电网负荷，不平衡功率由储能电池和大电网平衡。

运行模式4： 热负荷供应同模式2，风机和光伏供给微电网负荷，不平衡功率由储能、电动汽车及大电网平衡。

运行模式5： 热负荷供应同模式2，风机和光伏供给微电网负荷，不平衡功率由储能、电动汽车及大电网平衡，并考虑需求侧响应。

4.2 运行结果及分析

优化结果如表1所示。

表1 优化结果Table 1 Optimization results

由以上结果可知，在包含分布式发电(风机光伏)的微电网且考虑需求侧响应时，运维费用与运行模式无关。电能应该优先由风机和光伏发电供给。对比热电联供模式和热电独立供应模式的总运行费用，前者具有更好的经济效率，比后者高出11.36%。在微电网加入储能设备时，运行费用被进一步降低(见运行模式3)，而建设费用被提高了。对于电动汽车，不参与微电网调度的本质上是作为电负荷接入微电网，参与调度的实质承担的是储能电池的角色。电动汽车接入微电网后(见运行模式4)，运行费用增加了8元。值得注意的是，3辆不可调度的电动汽车入网后电力需求增加27 kW·h，而单位供电成本从0.63元/(kW·h)降低到0.62元/(kW·h)，下降了1.6%。加入需求侧管理起到了削峰填谷的效果，同时运行费用也减少到2 650.93 元，相比于运行模式4降低了2.2%。各模式总运行费用及碳排放处理费用对比见图2。由图2可知，运行模式1的碳排放处理费用最小，但其总费用远高于运行模式5，运行模式2、3由于向大电网购电，相较于其他模式，碳处理费用较高，综合比较，运行模式5运行下，系统具有经济最优性和良好的低碳效益。

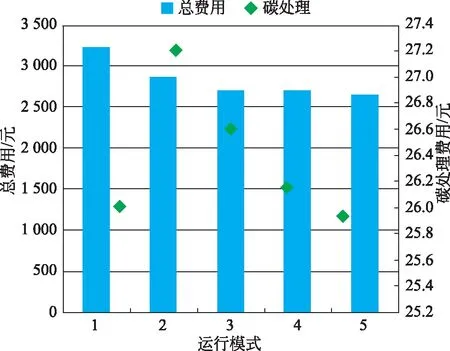
图2 各运行模式碳处理及总费用对比Fig.2 Comparison of Ccb and C in each case

在解决能源优化调度问题上，本文所用的萤火虫算法寻优能力要优于基本粒子群算法。2种算法对比之下，萤火虫算法寻优速度更快，收敛性更好，证明了本文算法的有效性。2种算法对比见图3。

图3 FA与改进FA对比Fig.3 Comparison between FA and modified FA

5 结论

本文以风-光-储-热电联供微电网为研究对象，并考虑需求侧响应及电动汽车特性，以总运行费用最小为目标函数，建立了优化调度模型，在目标函数中加入碳处理费用，对优化方案的选取考虑地更全面。将萤火虫算法应用到优化调度问题中，通过算例分析，证明文中所用算法比基本粒子群算法具有更好的信息搜索能力，能有效求出全局最优解。

CHP运行方式实现了能量的梯级利用，其运行总费用比热电独立供能时要低。微电网中接入储能和电动汽车，有效地调节了系统的峰谷负荷，且进一步降低了系统的运行费用，碳排放处理费用也有所下降，低碳效益更好。在此基础上再加入需求侧管理，不仅运行费用降幅更大，还能进一步降低用户供电费，达到更好的低碳效益。

[1] 吴雄, 王秀丽, 别朝红, 等. 含热电联供系统的微网经济运行[J]. 电力自动化设备, 2013, 33(8): 1-6. WU Xiong, WANG Xiuli, BIE Zhaohong,et al. Economic operation of micro grid with combined heat and power system[J]. Electric Power Automation Equipment, 2013, 33(8): 1-6.

[2] 王锐, 顾伟, 吴志. 含可再生能源的热电联供型微网经济运行优化[J]. 电力系统自动化, 2011, 35(8): 22-27. WANG Rui, GU Wei, WU Zhi. Economic and optimal operation of a combined heat and power microgrid with renewable energy resources[J]. Automation of Electric Power Systems, 2011, 35(8): 22-27.

[3] 李锋, 赵玺灵, 付林. 燃气轮机热电联供系统性能评估案例[J]. 热能动力工程, 2010, 25(1): 34-38, 119-120. LI Feng, ZHAO Xiling, FU Lin. Performance evaluation case of a gas turbine-based heat-and-power cogeneration system[J]. Journal of Engineering for Thermal Energy and Power,2010,25(1): 34-38， 119-120.

[4] 丁宁, 吴军基, 邹云. 基于DSM的峰谷时段划分及分时电价研究[J]. 电力系统自动化, 2001, 25(23): 9-12, 16. DING Ning, WU Junji, ZOU Yun. Research of peak and valley time period partition approach and tou price on DSM[J]. Automation of Electric Power Systems,2001, 25(23): 9-12, 16.

[5] 马玲玲, 杨军, 付聪, 等. 电动汽车充放电对电网影响研究综述[J]. 电力系统保护与控制, 2013, 41(3): 140-148. MA Lingling, YANG Jun, FU Cong, et al. Review on impact of electric car charging and discharging on power grid[J]. Power System Protection and Control, 2013, 41(3): 140-148.

[6] 项顶, 宋永华, 胡泽春, 等. 电动汽车参与V2G的最优峰谷电价研究[J]. 中国电机工程学报, 2013, 33(31): 15-25, 2. XIANG Ding, SONG Yonghua, HU Zechun, et al. Research on optimal time of use price for electric vehicle participating V2G[J]. Proceedings of the CSEE, 2013, 33(31): 15-25, 2.

[7] 黄伟, 黄婷, 周欢, 等. 基于改进微分进化算法的微电网动态经济优化调度[J]. 电力系统自动化, 2014, 38(9): 211-217. HUANG Wei, HUANG Ting, ZHOU Huan, et al. Dynamic economical dispatch for microgrid based on improved differential evolution algorithm[J]. Automation of Electric Power Systems, 2014, 38(9): 211-217.

[8] 洪博文, 郭力, 王成山, 等. 微电网多目标动态优化调度模型与方法[J]. 电力自动化设备, 2013, 33(3): 100-107. HONG Bowen, GUO Li, WANG Chengshan, et al. Model and method of dynamic multi-objective optimal dispatch for microgrid[J]. Electric Power Automation Equipment, 2013, 33(3): 100-107.

[9] 杨毅, 雷霞, 叶涛, 等. 考虑安全性与可靠性的微电网电能优化调度[J]. 中国电机工程学报, 2014, 34(19): 3080-3088. YANG Yi, LEI Xia, YE Tao, et al. Microgrid energy optimal dispatch considering the security and reliability[J]. Proceeding of the CSEE， 2014, 34(19): 3080-3088.

[10] 顾伟, 吴志, 王锐. 考虑污染气体排放的热电联供型微电网多目标运行优化[J]. 电力系统自动化, 2012, 36(14): 177-185. GU Wei, WU Zhi, WANG Rui. Multi-objective optimization of combined heat and power microgrid considering pollutant emission[J]. Automation of Electric Power Systems, 2012, 36(14): 177-185.

[11] 徐业琰, 彭思成, 廖清芬, 等. 考虑用户互补聚合响应与热能传输延时的综合能源园区运营商两阶段短期优化调度[J]. 电力自动化设备, 2017, 37(6): 1-11. XU Yeyan, PENG Sicheng, LIAO Qinfen, et al. Two-stage short-term optimal dispatch of MEP considering CAUR and HTTD[J]. Electric Power Automation Equipment, 2017, 37(6): 1-11.

[12] 白牧可, 唐巍, 吴聪, 等. 基于热网-电网综合潮流的用户侧微型能源站及接入网络优化规划[J]. 电力自动化设备, 2017, 37(6): 1-9. BAI Muke, TANG Wei,WU Cong, et al. Optimal planning based on integrated thermal-electric power flow for user-side micro energy station and its integrating network[J]. Electric Power Automation Equipment, 2017, 37(6): 1-9.

[13] LIU Z, CHEN C, YUAN J. Hybrid energy scheduling in a renewable micro grid[J]. Applied Sciences, 2015, 5(3): 516-531.

[14] 朱兰, 杨秀, 符杨. 含微型燃气轮机的微电网系统的优化规划研究[J]. 华东电力, 2011, 39(12): 2037-2040.

ZHU Lan, YANG Xiu, FU Yang. Optimal plan and design for microgrid including microturbine[J]. East China Electric Power, 2011, 39(12): 2037-2040.

[15] 帅暘, 冯丽, 祁佳, 等. 萤火虫算法的图像边缘检测[J]. 通信技术, 2015(8): 913-917. SHUAI Yang, FENG Li, QI Jia, et al. Image edge detection of glowworm swarm algorithm[J]. Communications Technology, 2015(8): 913-917.

[16] 骆东松, 李雄伟, 赵小强. 基于人工萤火虫的模糊聚类算法研究[J]. 工业仪表与自动化装置, 2013(2): 3-6. LUO Dongsong, LI Xiongwei, ZHAO Xiaoqiang. Research on fuzzy clustering algorithm based on GSO[J]. Industrial Instrumentation & Automation, 2013(2): 3-6.

[17] 刘翠苹, 张海涛, 白舸. 基于萤火虫群优化算法的无线传感器节点部署[J]. 计算机应用, 2013, 33(4): 905-907. LIU Cuiping, ZHANG Haitao, BAI Ge. Node deployment of wireless sensor network based on glowworm swarm optimization algorithm[J]. Journal of Computer Applications, 2013, 33(4): 905-907.

[18] 王晶, 王宗礼, 陈骏宇, 等. 基于萤火虫优化算法的微网源-荷博弈模型及分析[J]. 电力系统自动化, 2014, 38(21): 7-12. WANG Jing, WANG Zongli, CHEN Junyu, et al. A game model for dgs-loads in microgrid based on firefly algorithm and its analysis[J]. Automation of Electric Power Systems, 2014, 38(21): 7-12.

[19] 徐兢浩. 基于改进萤火虫算法的变电站选址定容研究[D]. 北京:华北电力大学, 2016. XU Jinghao. Research on substation locating and sizing based on improved firefly algorithm[D]. Beijing: North China Electric Power University, 2016.

靳现林

(编辑 蒋毅恒)

Hybrid Energy Micro Grid Optimal Scheduling Considering Low-Carbon Benefits

JIN Xianlin1, CAI Xiaoyu2

(1. Guohua Energy Investment Co., Ltd., Dongcheng District, Beijing 100007, China;2. North China Electric Power University, Changping District, Beijing 102206, China)

In recent years, micro grid technology including renewable energy generation has been developed rapidly. According to the problem that the energy efficiency of micro grids containing multiple new energy sources and new loads is low, this paper focuses on the optimal scheduling of hybrid energy micro grid, and considers the demand response and low-carbon benefits in the optimal scheduling model. In the optimization process, we take the microgrid which contains photovoltaic (PV), wind power, combined heat and power (CHP) and electric vehicles (EV) as the object of study, and construct the output models for each resource. The objective function aims to minimize the total cost including gas cost, operation and maintenance cost, electric power purchase from the main grid, depreciation charge for micro power and cost of carbon dioxide emission. Under the constraint conditions, we adopt the improved firefly algorithm (FA) to solve the objective function. With case study, we calculate the total operation cost of micro grid under different scenarios, analyze the low carbon benefits of each scheme, and seek the balance between economy and low carbon to obtain the optimal operation scheme of micro grid.

micro grid; optimal scheduling; hybrid energy; low-carbon benefits; demand side management

TM 73

A

2096-2185(2017)03-0026-07

10.16513/j.cnki.10-1427/tk.2017.03.005

2017-05-13

靳现林(1974—)，男，硕士，从事风电场运行管理工作，11680090@shenhua.cc；

蔡晓宇(1993—)，女，硕士研究生，研究方向为电网规划。