复合LINEX损失下k阶Erlang分布参数的Bayes估计

季海波

(宿迁学院 文理学院，江苏 宿迁 223800)

复合LINEX损失下k阶Erlang分布参数的Bayes估计

季海波

(宿迁学院 文理学院，江苏 宿迁 223800)

在复合LINEX对称损失函数下，利用Bayes估计的方法研究了k阶Erlang分布参数的Bayes估计和E-Bayes估计，并且通过随机模拟检验参数的Bayes估计和E-Bayes估计的合理性和优良性，结果表明：在复合LINEX对称损失函数下，k阶Erlang分布参数的Bayes估计和E-Bayes估计都是合理的，但是E-Bayes估计的精度更高。

k阶Erlang分布；复合LINEX对称损失函数；Bayes估计；E-Bayes估计

0 引言

在统计决策中，参数估计的优劣在很大程度上依靠损失函数的选择，常见的有LINEX损失函数、熵损失函数、对称熵损失函数、二次损失函数和平衡损失函数等损失函数下的Bayes估计。

而k阶Erlang分布的参数在不同损失下的Bayes估计暂时还没有研究结果，而在复合LINEX对称损失函数下的不同分布的参数的Bayes估计已有不少[1-2]。但是在复合LINEX对称损失函数下k阶Erlang分布参数的Bayes估计和E-Bayes估计还没有相关研究成果。

张睿[3]提出的复合LINEX对称损失函数，其表达式如下：

L(θ,δ)=La(θ,δ)+L-a(θ,δ)=e-a(θ,δ)+ea(θ,δ)-2,a>0

(1)

本文在复合LINEX对称损失函数下，研究k阶Erlang分布Bayes估计和E-Bayes估计，并通过随机数值模拟检验参数θ的Bayes估计和E-Bayes估计的合理性与优良性。

1 参数θ的Bayes 估计

k阶Erlang分布的随机变量是k个独立的不同参数的指数分布随机变量的和，它是一种Phase-Type分布，是亚指数分布的一个特例(各阶指数过程的均值都相等的阶亚指数分布就是k阶Erlang分布)，而指数分布是k阶Erlang分布的特例。相比于指数分布，k阶Erlang分布能够更好地对现实数据进行拟合(更适用于多个串行过程，或者无记忆性假设不显著的情况下)，故在排队论中被广泛应用，在保险金融中也被用作索赔分布。

定义1[4]若X1，X2，…，Xk是一列独立的随机变量，且都服从指数分布E(μ)，则随机变量T=X1+X2+…+Xk具有概率密度，

或者等价地，其分布函数为，

称T服从参数为μ的k阶Erlang分布。

为便于估计，令θ=kμ，则k阶Erlang分布的密度函数为:

(2)

其中θ>0。

从k阶Erlang分布中抽取容量为n的简单样本T1,T2,…,Tn，记T=(T1,T2,…,Tn)，t=(t1,t2,…,tn)为T的观测值，则样本t的似然函数为，

(3)

首先讨论k阶Erlang分布参数θ的Bayes估计。

引理1 在复合LINEX对称损失函数(1)下，对任何先验分布π(θ)，θ的Bayes估计为:

(4)

选取Γ(α,β)为k阶Erlang分布参数θ的先验分布，则先验分布的密度函数为，

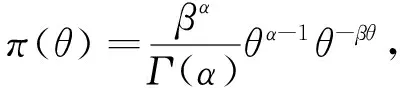
(5)

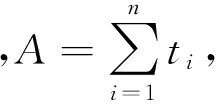
证明：参数θ的后验密度函数为，

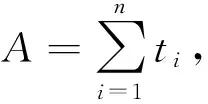
则由引理1及定理1可得k阶Erlang分布参数θ的Bayes估计。

定理2 在损失函数(1)下，对于先验分布Γ(α,β),k阶Erlang分布参数θ的Bayes估计为，

证明：由定理1有

(6)

(7)

由(6)(7)及引理1可得,

2 参数θ的E-Bayes 估计

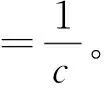
下面引入E-Bayes估计的定义：

定义2[6]若δB(α,β)是参数θ的Bayes估计，含有超参数α,β，并且δB(α,β)是连续的，则称，

(8)

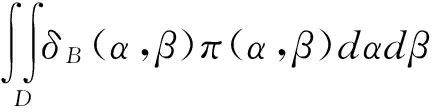
则由超参数α,β的先验分布的假设及E-Bayes估计的定义有下列定理。

定理3 对于k阶Erlang分布，若参数θ的先验分布为Γ(α,β)，超参数α,β的先验分布为D上的均匀分布，则参数θ的E-Bayes估计为：

其中f(x)=xlnx。

证明：由E-Bayes估计定义可得

其中f(x)=xlnx。

3 随机模拟

当时给定参数的真值，根据分布(2)利用Monte Carlo方法随机模拟一组不同样本容量的随机样本，通过模拟参数的Bayes估计和E-Bayes估计来验证其合理性、优良性，模拟中取得模拟结果见表1和表2。

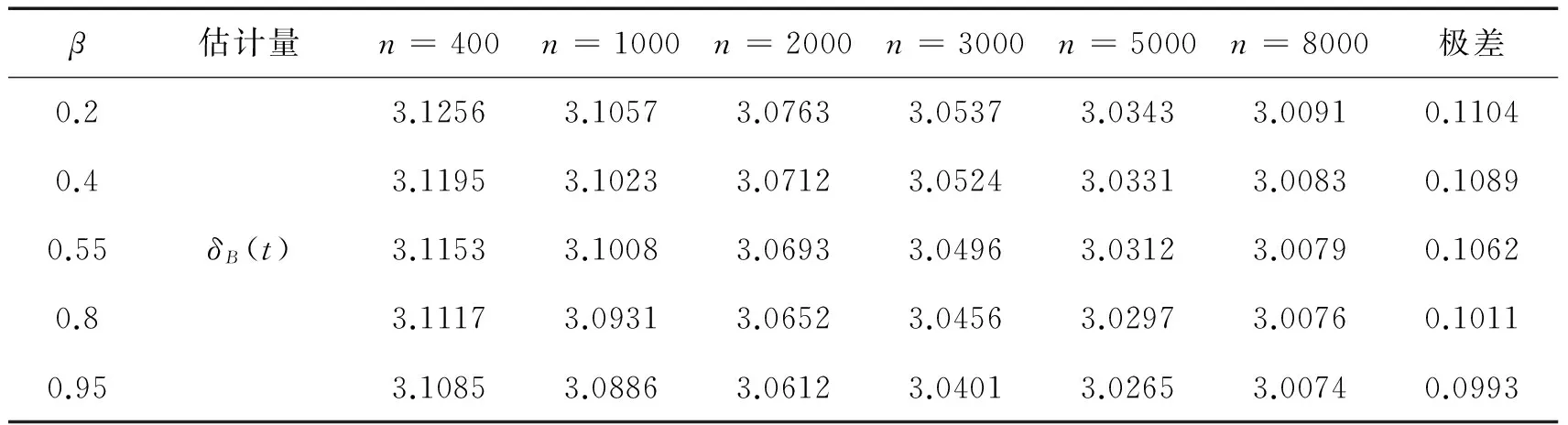
表1 不同样本容量下参数θ的Bayes估计

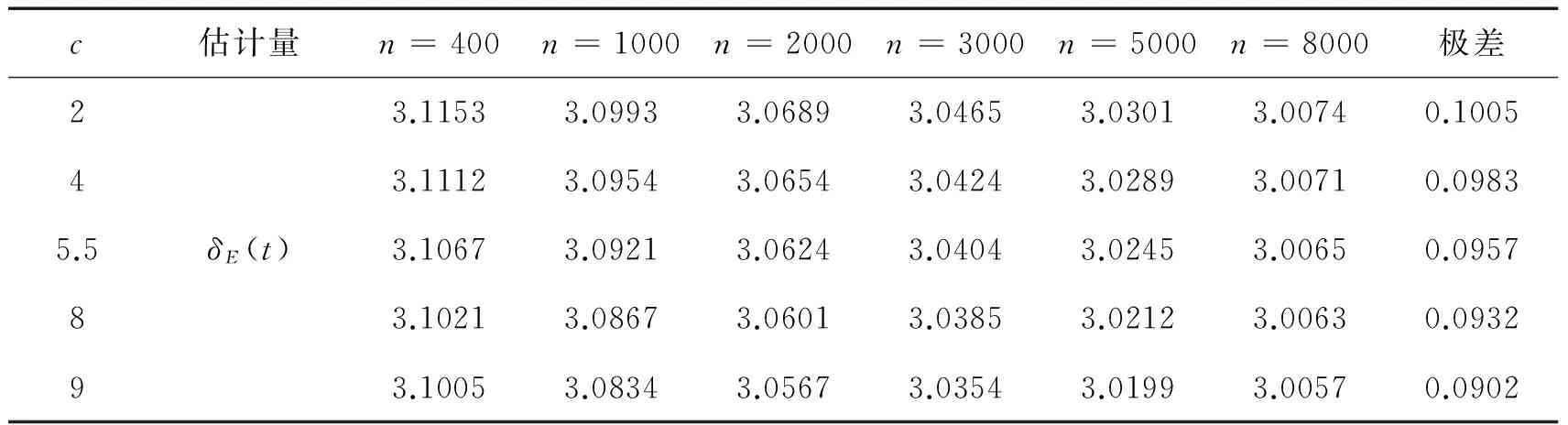
表2 不同样本容量下参数θ的E-Bayes估计

由上述模拟结果表明：从极差方面来看，表1和表2中体现出来的每个估计的极差都不大，参数的Bayes估计和E-Bayes估计的估计值与真值的偏差都很小，最大只有0.1104和0.1005，而且不管是参数的Bayes估计还是E-Bayes估计，它们的估计值都会随着样本量的增加而更加接近于参数的真值3.故可以看出k阶Erlang分布参数的Bayes估计和E-Bayes估计都是合理的，而且当样本容量较大时，E-Bayes估计会更优。

[1] 韦程东,韦师,苏韩.复合LINEX对称损失下Pareto分布形状参数的E-Bayes估计及应用[J].统计与决策,2009(17):7-9.

[2] 韦师,李泽衣.复合LINEX对称损失下BurrXII分布参数的Bayes估计[J].高校应用数学学报,2017(1):49-54．

[3] 张睿.复合LINEX对称损失下的参数估计[D].大连:大连理工大学,2007.

[4] 胡运权.运筹学基础及应用[M].北京：高等教育出版社,1986.

[5] 韩明.参数的E-Bayes估计及其应用[J].数学的实践与认识,2004(9): 97-106.

[6] 韩明.Pascal分布的参数估计[J].纯粹数学与应用数学,2006(4): 510-514.

[7] 茆诗松,王静龙.高等数理统计[M].北京:高等教育出版社,1998.

[8] 茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999.

[9]JamesOBerger. 统计决策论及贝叶斯分析[M]. 贾乃光,译. 北京:中国统计出版社,1998.

(责任编辑：孙文彬)

Bayes Estimation ofk-th Erlang Distribution Parameter in the Composite LINEX Loss of Symmetry

JI Hai-bo

(School of Liberal and Science, Suqian College, Suqian Jiangsu 223800, China)

Based on the compound LINEX asymmetric loss function, the paper studies the Bayes estimation and E-Bayes estimation ofk-th Erlang distribution parameter, and makes a random numerical simulation test on rationality and optimality of the parameter's Bayes estimation and E-Bayes estimation. The results show that using this method to estimate the parameter ofk-th Erlang distribution are reasonable and feasible, and the E-Bayes estimation is better than Bayes estimation.

k-th Erlang distribution; composite LINEX loss of symmetry; Bayes estimation; E-Bayes estimation

2017-04-27

季海波(1981-),男,江苏南通人,讲师,硕士,主要从事概率统计研究。

O212.62

A

1009-7961(2017)03-0097-04