基于灰色模型GM(1,1)的淮安市旱灾预测

臧庆佩，顾文慧

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

基于灰色模型GM(1,1)的淮安市旱灾预测

臧庆佩，顾文慧

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

近年来，随着科学技术的不断发展，研究干旱灾害的变化趋势已符合当今科学和自然规律，并具有一定的研究性。利用淮安市统计年鉴上8年的降水量数据建立灰色预测灾变模型，对淮安市干旱年份进行预测，经残差检验以及后验差检验分析，模型精度高达80%以上。并对实测数据进行检验，效果较为理想，并对未来两年的干旱情况进行预测，结果表明不会发生干旱。

干旱；灰色灾变预测；精度检验；模型

0 引 言

干旱是主要的自然灾害之一，不仅对国民经济和社会发展产生严重影响，还会对生态环境的发展造成进一步的恶化。而且，干旱灾害属于规律性不强且非连续发生事件，其预测难度较大。

在全球气候变暖的背景下，开展干旱的评估、监测与预测研究，已成为政府和学术界高度重视的热点问题，且具有重大现实意义。与此同时，干旱问题逐步引起社会关注，而如何准确预测干旱情况的发展也成为气象部门重点关注的问题。因此，为了降低因干旱而导致的经济损失，对未来几年内淮安市干旱情况的预测是有必要的。

国内针对旱灾预测研究的方法也很多。李晓辉[1]利用BP神经网络与灰色模型相合的预测方法对朝阳地区进行干旱特征分析和预测，其模型精度高，预测误差小；木沙·如孜[2]通过灰色灾变理论，建立旱灾灰色灾变预测GM(1,1)模型，对塔河流域未来5年旱灾进行了分析预测，模型预测效果好。王艺璇[3]通过基于SWAT模型对不同类型干旱指标进行关系分析及预测，描述了干旱的时空变化分布特征，其预测值可靠。

由于所获得的资料数据有限，且是短期预测，综合以上对干旱的研究，本文根据淮安市2008年～2015年降水量数据建立灰色灾变模型，对淮安市未来两年降水量分布变化特征进行分析，预测是否出现干旱情况，并对预测结果进行检验，为合理利用和开发水资源、防灾减灾、生态服务建设等提供参考意见。

1 灰色系统理论

灰色系统理论以“部分信息已知及部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控[4]。

灰色预测模型又称为模型。表示1阶的、1个变量的微分方程型模型，是最常用的灰色预测模型[5]。其建模过程首先通过对规律性不强的原始序列进行一次累加，生成近似按指数规律变化的序列。

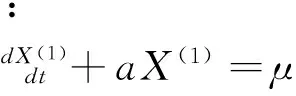
(1)

其中：a为发展系数；μ为灰色作用量；t为时间变量；X为时间变量的函数。

式(1)的离散解为：

(2)

其中：k=0,1,2,…；参数a、μ可通过最小二乘法[7]求得；e为自然对数的底，取值为2.718。

由式(2)可得出预测模型为：

(3)

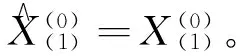
2 干旱预测实证分析

通过查询淮安市统计年鉴的年平均降水量数据，得出2008年～2015年降水量数据，见表1。

表1 淮安市2008 ～ 2015 年降水量统计 (mm)

2.1 模型建立

(1)应用MATLAB软件进行数据预处理，得到新的原始数据序列：

X(0)={979.1,982.6,992.6,1001.6,1014.2,1039.8,1087.4,1123.4}

(2)对X(0)通过一次累加生成新序列，结果见表2。

表2 一次累加生成序列

(3)构造矩阵B和数据向量Yn。

其中，i=1,2,…,7。

其中，j=2,3,…,8。

则，α=-0.0227，μ=932.1374。

(5)将α、μ代入式(3)，得：

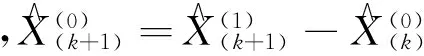
2.2 模型精度检验

灰色预测模型的精度检验有三种方法：关联度检验，后残差检验，相对误差大小检验。本文采用后残差检验和相对误差检验。

(1)相对误差检验：

所得的残差序列为

ε(0)=(ε(1),ε(2),ε(3),ε(4),ε(5),ε(6),ε(7),ε(8))

即，

综上所述，我国土建工程发展进程较长，深基坑支护技术应用效果也比较成熟，随着技术人员开发效果深入，更多施工技术被研究出来，我国疆域辽阔，地貌多样，为满足各地区建筑工程要求，提高对工作人员生命安全财产的维护，就需要对应单位在前期设计合理规划，并投入使用正确的施工技术。

ε(0)=(35.5007,17.2958,5.0987,8.6031,19.1260,17.3021,6.0001,17.1554)

相对误差公式为，

则，φ(i)=(0.0363,0.0176,0.0051,0.0086,0.0189,0.0166,0.0055,0.0153)

因为相对误差小于0.5%，所以模型的精度较高。

(2)后残差检验：

原始序列的标准差为，

绝对误差序列的标准差为，

求得的均方差比C为，

由于根据指标C和P将预测等级划分为4等[8]，见表3。

表3 预测精度等级

而所得的C<0.5，P>0.80。所以GM(1.1)模型检验合格，有较好的精确度，可用该模型对淮安市未来两年可能发生的干旱年份进行预测。

2.3 应用GM(1.1)模型进行预测

利用公式(3)进行预测，所得结果如下，

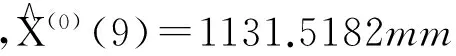
结合图形与计算结果，说明2016年、2017年淮安市将不会发生干旱现象。且实际是在2016年也并未发生干旱现象，所以，预测结果合理可信。

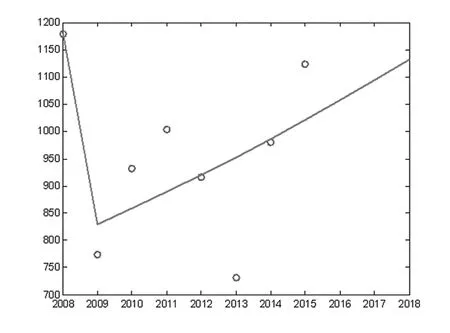
图1 淮安市2008年～2015年平均降水量分布图

3 结论

根据以上分析，可以得出如下结论：

(1)2008年～2015年淮安市的年降水量总体上呈增加的趋势，所以，发生干旱的可能性减小。利用灰色理论建立的预测模型对干旱预测结果显示，2016年预测结果与实况相符。

(2)要使预测结果更为准确，可以利用上述的灰色预测模型多次取长度不等的数据序列进行建模，从而可产生多个预测值，最后根据这多个预测值的分布确定预测区间，提高精度。

(3)由于灰色预测模型的预测值是一个灰区间，资料样本长度不同，预测值具有不确定性。所以，利用灰色系统理论的分析方法建立气候灾变预测模型，所用的资料长度应当适宜。如果序列太短，参加计算的信息太少，预测结果容易失真，同时，如果序列太长，就会难以满足序列所要求的光滑度，也会造成预测失败。

[1] 刘晓辉.朝阳地区干旱特征分析和预测方法研究[D].沈阳：沈阳农业大学，2013.

[2] 木沙·如孜.塔里木河流域干旱灾害特征及其成因分析[D].乌鲁木齐：新疆农业大学，2013.

[3] 王艺璇.基于SWAT模型的不同类型干旱指标关系分析及预测[D].郑州：郑州大学，2014.

[4] 刘思峰,谢乃明.灰色系统理论及应用[M].北京：科学出版社，2008.

[5] 张浩,朱庆明,刘秀玉,等.基于指数平滑法的光催化涂料效果灰色预测模型及应用[J].涂料工业，2013(1)：28-29.

[6] 李又君,孙培良,孙青然,等.灰色预测模型及干旱预测[J].山东气象学报，2012(1)：7-8.

[7] 邱淑芳,王泽文.灰色模型背景值计算的改进[J].统计预测与决策，2007(1)：129-131.

[8] 徐国祥.统计预测与决策[M].上海：上海财经大学出版社，2016.

(责任编辑：孙文彬)

Drought Forecast of Huaian City Based on Grey Model GM (1,1)

ZANG Qing-pei, GU Wen-hui

(School of Mathematical Science, Huaiyin Normal University, Huai'an Jiangsu 223300, China)

In recent years, with the continuous development of science and technology, studying the drought has been in line with the laws of science and nature. Therefore, it has research value. A grey system disaster prediction model, which was used to forecast the dry years of Huai'an, was set up with eight years' observed rainfall data from Huai'an statistical yearbook. Then, we made the test of residual errors and after-checking errors. The results show that the model accuracy is more than 80%. At the same time, the test with the observed data was also made and ideal results were obtained. Moreover, the drought possibility in the following two years is predicted, and the results show that there will be no drought happening.

drought; grey disaster prediction; accuracy test; model

2017-02-21

国家自然科学基金(11401245)；江苏省高等学校大学生创新创业训练计划(201610323043X)

臧庆佩(1982-)，男，江苏淮安人，副教授，博士，主要从事概率论与数理统计研究。

O211

A

1009-7961(2017)03-0093-04