基于改进权重非局部均值图像滤波方法与实现
2017-07-24张玉荣
张玉荣
(1.武汉理工大学 信息工程学院,武汉 430070;2.徽商职业学院 电子信息系,合肥 230061)
基于改进权重非局部均值图像滤波方法与实现
张玉荣1,2
(1.武汉理工大学 信息工程学院,武汉 430070;2.徽商职业学院 电子信息系,合肥 230061)
图像滤波是计算机图像处理领域中极为重要的预处理环节,目的是消除混杂在图像中的干扰因素,改善图像质量,强化图像表现特征。在传统非局部均值滤波算法基础上,提出了基于改进权重的非局部均值图像滤波算法,以欧式距离高斯加权为基础,配以图像之间的自相似性,在图像领域灰度值的矩阵间使用,充分地将图形领域间的自相似性发挥出来。实验结果表明,基于改进权重的非局部均值图像去噪算法比传统的非局部均值去噪算法保持更有效的图像结构信息。
加权权证;非局部均值;图像滤波;图像相似性
0 引言
由于受多方面因素的影响,人们在使用计算机对图像进行处理的过程中,不可避免地受到各种噪声的干扰,噪声会导致图像信号质量的严重下降,且有噪声的图像往往会损失部分有效信息,从而影响到视觉效果,不利于后期图像分析。因此,对图像进行滤波去噪已经成为图像处理领域极为关键的预处理环节。图像噪声并不限于人眼所能看得见的失真和变形,有些噪声只有在进行图像处理时才可以发现。
图像滤波是图像处理方面最基础且最重要的内容,图像滤波的目的就是去除图像在传输或者获取中的噪声污染,图像去噪的效果直接影响到包括目标识别、图像分割、边缘提取等方面图像的后期处理,其中去除图像叠加高斯白噪声,是图像滤波中的重点研究内容。如果图像滤波算法能够满足一定的目标,那么这个算法就是最理想的。为了得到最理想的算法,研究人员提出了多种滤波方式。传统的去噪算法有卡尔曼滤波、中值滤波、小波变换等。本文在传统算法基础上深入研究,尤其是局部均值滤波去噪算法,针对该算法结合局部二值在改进权重基础上,让相似度高的邻域获得的权重越大,而相似度低的邻域获得的权重越小,在高斯加权的欧式距离基础上,结合相关系数来衡量信号之间相关程度的指标,能够更好地表现出图像领域之间的相似性。为此提出一种效果与效率兼备的图像去噪方法,并结合国际标准Lena图像检验其实际应用效果,最后通过硬件改进达到图像实时处理的目的,实验结果表明,该方法在去噪效果和实时性上得到了很好的平衡。
1 图像滤波算法
图像滤波应该满足:保持图像纹理细节不被丢失;保留图像边缘不模糊;过滤图像噪声;保持图像平滑区光滑;图像不引入人造特征[1]。图像去噪算法分为基于局部的滤波和基于非局部的滤波。
1.1 基于局部的滤波算法
被广泛应用的基于局部的滤波为高斯滤波,它是在空域上使图像与线性对称正定核函数进行卷积计算,高斯滤波的高斯核可以表示为:
Gh(x)=(1/4πh2)e(|x|2/4h2)
(1)
其中,h为高斯核标准差,表示不同值的不同平滑程度的高斯核。
定义方法噪声,将图像设为u,Dh表示为参数h的去噪算子,那么图像u的噪声为:
n(Dh,v)=u-Dh(u)
(2)
式(2)表示原始图像和去噪之后图像的差,方法噪声要求与白噪声相接近,以使图像不会因为去噪而丢失其他内容。
高斯滤波的方法噪声表示为:
u-Gh*u=-h2△u+o(h2)
(3)
去噪的性能与平滑领域大小有着密切的联系,能够通过平均抑制噪声。假设h=kε,k是h之间对u和n的采样数量,它的值比1大,并且能够去除噪声。高斯的平滑效果要通过参考像素点i=0的结果进行评价,上式表示为:
(4)
n(x)是分段常量函数,pi是以像素点i为中心,以ε2为大小的正方形点集,Gh(i)是高斯核函数Gh的均值。
随机向量X的方差表示为Var(X),那么随机变量方差就可以表示为:
Var(Gh*n(0))=∑ε4Gh(i)2δ2/8πh2
(5)
尺度h比抽样尺度ε的平滑区域大时,图像去噪不会改变位置的灰度。图像的谐波部分高斯滤波方法噪声为零时,边缘或纹理附近值就会变得很大。所以,高斯卷积对平坦区域有良好的去噪效果,但是在边界或者纹理地方就会比较模糊[2]。
1.2 非局部均值滤波算法
假设噪声的图像模型为:
Y(a)=X(a)+N(a)
(6)
其中噪声图像表示为Y(a),没有受到噪声干扰的图像表示为X(a),均值表示为N(a),高斯白噪方差为σ2。对图像进行去除噪音的目的是从噪音图像中取得原始图像的最佳估计值,使最佳估计值最大限度的接近原始图像[3]。
假设有一幅噪声图像v={v(a)|a∈A},A为图像中的坐标域,对图像中的某一个像素点a进行非局部均值滤波去噪,计算之后的噪点估计值为:

(7)
其中权值w(a,b)与像素点a,b之间的相似性有一定的关系,并且满足0≤w(a,b)≤1和∑bw(a,b)=1。
像素a,b之间相似性的确定通过灰度矩阵Na和Nb的相似进行确定,Na为像素a的图像区域,Nb为像素b的图像区域。每个区域之间的相似度的度量通过区域间的高斯加权欧式距离d(a,b)进行,可以表示为:

(8)
其中,β>0为高斯核的标准差。图像区域间的灰度值矩阵相似度越高,其像素点在加权平均后的权重就会越来越大,权重表示为:
(9)
其中,z(a)=exp(d(a,b)/r2)表示为归一化常数,r为平滑参数,使指数函数的衰减速度能够得到有效控制[4]。
2 基于改进权重的非局部均值图像滤波算法
在传统的非局部均值图像滤波去噪算法中,加权核函数影响去噪效果。良好的核函数特性包括:具有较高相似度邻域要有较大的权重;具有较低相似度领域要有较小的权重。在非局部去噪算法中,确定加权核函数是尤为重要的。传统的非局部均值去噪算法中,一般使用指数型核函数:
f(x)=exp(f(d(i,j))/h2),d(i,j)≤h
(10)
为了能够有效解决传统非局部均值去噪中的不足,可以将其融入图像领域间的相关系数,以此衡量图像间的指标,评价图像块之间的相似性,其主要表示为:
(11)
其中,ψ(a,b)=∑a*b,a1表示为灰度矩阵Na的灰度均值;b1表示为灰度矩阵Nb的灰度均值。
在传统非局部均值去噪算法中,通过图像邻域的高斯加权欧氏距离d(a,b)表示灰度矩阵间的相似性,如果d(a,b)与0相接近,表示邻域灰度矩阵具有较高的相似度,式(11)中CR(a,b)的值在-1和1之间,为了使传统非局部均值去噪算法能够与改进的算法的距离相似,可将邻域灰度矩阵的相似参数表示为:
w(a,b)=1-CR(a,b)/2
(12)
其中,w(a,b)的值在0~1之间,如果两个邻域灰度矩阵相同,w(a,b)的值就为0;如果w(a,b)的值越来越大,那么两个邻域灰度矩阵就会越来越不相似。使两个邻域之间的相似参数w(a,b)和传统非局部均值去噪算法的高斯加权欧氏距离相融合,全新的邻域灰度矩阵相似性参数就可以表示为:

(13)

3 实验结果
使用MATLAB进行实验的过程中,分别从图像的去噪效果、方法噪声、峰值信噪比三个方面进行测试比较。由于非局部均值去噪算法具有较大的计算量,所以为了能够有效提高算法的效率,将改进后的非局部均值去噪算法和传统的非局部均值去噪算法使用限定邻域,根据多次算法测试参数的经验值,相似窗为7*7,搜索窗为21*21的参数,添加均值为0,标准方差为30,实验图像采用国际标准测试图像Lena图像,图像大小为512×512,如图1所示。

图1 实验图像:(a) Lena原灰度图;(b) Lena添加噪声的灰度图
3.1 去噪结果比较
图2通过图像灰度变换增强后采用传统非局部均值图像去噪算法与改进非局部均值图像去噪算法的对比结果,可以看出来,改进后的非局部均值图像去噪算法比传统非局部均值图像去噪算法的视觉效果要好很多,尤其是在一些纹理地方和细节方面,改进后的非局部均值图像去噪算法最大限度地保留了原始图像中的细节信息。
为了能够使两者的对比效果中的细节信息更加明显和清晰,给出去噪之后的Lena图局部细节的放大图片,如图3所示。通过对比和观察可以看出来,使用改进后的非局部均值算法去噪之后的图像具有大量且清晰的结构信息,无论从局部还是从整体来看,改进后的非局部均值算法都比传统非局部均值去噪算法要优异得多。
3.2 方法噪声对比
方法噪声对比是一种全新的评价图像去噪性能的标准,将其定义为含有噪音图像的去除噪音图像的差。为了充分发挥改进非局部均值算法的优点,给出了传统非局部均值图像去噪算法和改进非局部均值去噪算法处理之后的方法噪声,并进行对比,可以了解传统非局部均值去噪算法处理之后得到的噪声具有多种细节信息,改进后的非局部均值去噪算法处理之后得到的噪声具有较少的细节信息,这表明改进后的非局部均值去噪算法具有较良好的性能[5],如图4所示。

图2 Lena图去噪效果对比:(a)传统非局部均值算法去噪效果;(b)改进非局部均值算法去噪效果

图3 Lena图去噪细节效果对比:(a)传统非局部均值算法去噪细节效果;(b)改进非局部均值算法去噪细节效果

图4 Lena图方法噪声对比:(a)传统非局部均值算法噪声;(b)改进非局部均值算法噪声
噪声标准差传统非局部均值去噪算法改进非局部均值去噪算法PSNR/dBαPSNR/dBα1019.2540.97419.9210.9792016.2350.94116.9540.9623014.4510.89915.0150.935

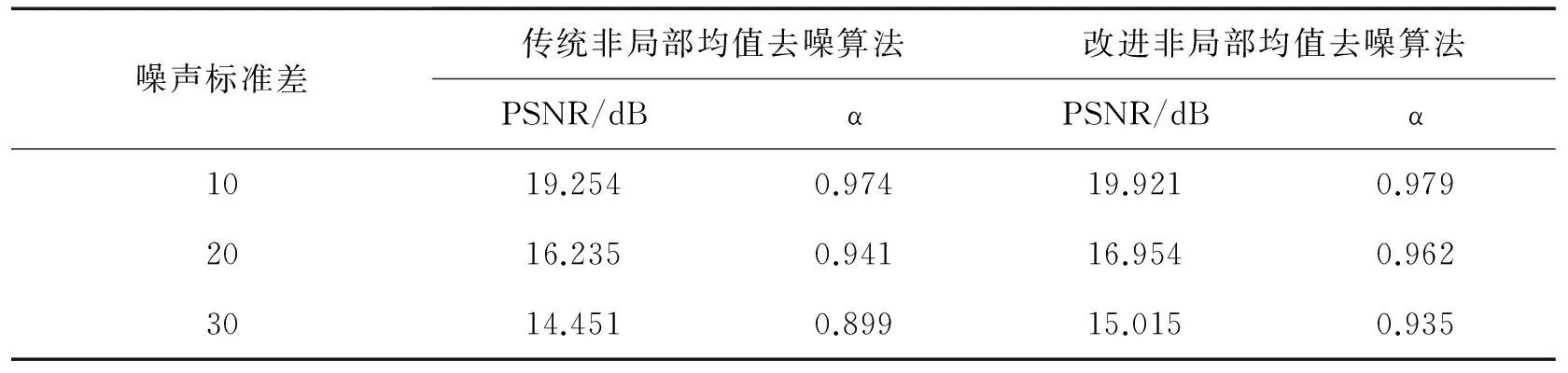
图5 Lena图像两种算法的峰值信噪比
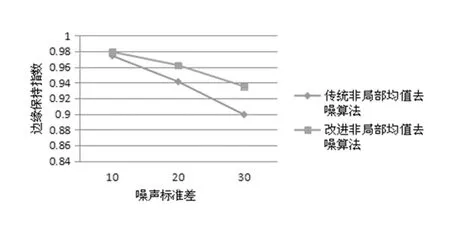
图6 Lena图像两种算法的边缘保持指数
3.3 对比峰值信噪比和边缘保持指数
为了能够充分体现改进非局部均值算法的优势,对图1中的两幅图像融入了标准差为10、20、25、30的高斯白噪声,噪声均值为0,两种方式对应的边缘保持指数α和峰值噪声比(PSNR)的测试结果见表1,在不同的噪声中使用改进非局部均值图像去噪算法,其去噪性能和边缘保持指数比传统非局部均值去噪算法要良好。图5和图6分别给出了两种算法在不同噪声中的峰值信噪比和边缘保持指数,能够更加直观和清晰地看出两者的性能差异。对比看出,改进非局部均值去噪算法比传统非局部均值去噪算法有更好的结构信息保持度和峰值信噪比[6]。
4 结论
综合以上实验结果与分析可知,改进的非局部均值滤波去噪算法是在改进权重基础上,让相似度高的邻域获得的权重越大,而相似度低的邻域获得的权重越小。在高斯加权的欧式距离基础上,结合相关系数来衡量信号之间相关程度指标,能够更好地表现出图像邻域间的相似性。
对含有较多纹理和细节信息的图像测试表明,相对于传统的非局部均值滤波去噪算法,基于改进权重的非局部均值图像去噪算法在去噪性能和细节处理方面能力更强,输出峰值信噪比更高。
实验还发现,本文提出的算法可以应用在各种序列图像的前期预处理过程中,尤其对于噪声强度越大的图像,去噪性能越明显,去燥后的图像视觉效果越好,在去噪效果和计算速度上得到了很好的平衡。
[1] 刘晓明,田雨,何徽,等.一种改进的非局部均值图像去噪算法[J].计算机工程,2012(4):199-201.
[2] 房宜汕.基于改进的非局部均值去噪算法[J].软件,2014(2):59-62.
[3] 黄玲俐.一种改进权重的非局部均值图像去噪方法[J].计算机技术与发展,2016(6):16-19.
[4] 王林.基于非局部均值的图像去噪方法研究[D].西安:西安电子科技大学,2014.
[5] 刘卓亚.非局部均值图像去噪算法研究[J].电脑知识与技术,2012(22):5448-5449.
[6] 周兵,韩媛媛,徐明亮,等.快速非局部均值图像去噪算法[J].计算机辅助设计与图形学学报,2016(8):1260-1268.
(责任编辑:孙文彬)
Research on the Non-local Mean Image Filtering Algorithm Based on Improved Weight
ZHANG Yu-rong1,2
(1. School of Information Engineering, Wuhan University of Science and Technology, Wuhan 430070, China; 2. Electronics Information Department, Huishang Vocational College, Hefei 230061, China)
Image filtering is an important step in the field of computer image processing, the purpose is to eliminate the confounding factors in the image, improve the image quality, and strengthen the image performance. The non local mean denoising uses the self similarity between the image domains to construct the weights, and then to restore the image, the smaller is the distance, the greater is the weight. This paper proposed the non local means denoising algorithm based on improved image weights, the Euclidean distance weighted Gauss based, with self similarity between images and its use in the field of image gray value matrix, full graphic field of self similarity between play. Experimental results showed that the non local mean image denoising algorithm based on the improved weight is more effective than the traditional non local mean denoising algorithm.
weighted warrant; non local means; image filtering; image similarity
2017-05-05
安徽省高校自然科学重点项目(KJ2016A685);安徽省教育厅质量工程项目(2014jxtd110,2015tszy089)
张玉荣(1976-),女,安徽庐江人,副教授,在读博士,主要从事视频图像处理和物联网技术应用研究。
TP391
A
1009-7961(2017)03-0001-05
