数列中参数值的确定方法研究

艾菊梅

(江西省抚州市临川一中,江西 抚州 344000)



数列中参数值的确定方法研究

艾菊梅

(江西省抚州市临川一中,江西 抚州 344000)

参数值问题是高中阶段数学教学中的重要教学内容，也是高考中的主要考点，该部分教学内容的难度较大，成为高中阶段数学教学中的难点教学内容，学生在实际的解题过程中，常常存在对题目感到无从下手的情况，面对难度较大的题望而却步，影响着学生的数学学习成绩.本文选择一些典型的数列参数值，对其确定的方法进行介绍，对学生今后的学习提供理论性的指导.

数列；参数值；确定方法

数列中参数值教学一直是高中数学中的重难点教学内容，该知识点自身具有综合性强、使用范围广、涉及到的知识点多等特点，在实际的解题过程中，要求学生具有灵活的思维，题目会以多样化及新颖化的形式出现，重点考查学生对知识点的理解能力，要求学生掌握解题技巧，做好数列中参数值相关知识点的归纳及整理是数学教师需要迫切解决的问题，也是提高数学教学效果的关键.

一、特殊值法

特殊值法是数列参数值解题中的一种常见解题方法，某一命题会在一般情况下出现，命题自身具有较强的特殊性，在解题过程中需要结合题目中的已知条件，通过对命题进行架设的过程，使特殊命题成立，进而求出相关参数的值.

例1 数列{an}满足a(n+1)=3an+n(n属于正整数),是否存在a1,使{an}成等差数列？

解 首先假设存在a1使{an}成等差数列,则a1+a3=2a2,设公差为d.由{an}满足a(n+1)=3an+n可知a2=3a1+1；a3=3a2+2=3(a1+d)+2.因此a1+3(a1+d)+2=2(3a1+1)，化简后得a1=3d/2.

由于公差为d,所以a2=a1+d=5d/2；a3=a2+d=7d/2；a3=a2+d=9d/2.

又由于{an}满足a(n+1)=3an+n,a2=3a1+1=1+9d/2；a3=3a2+2=2+15d/2；a4=3a3+3=3+21d/2.

则：d=a4-a3=a3-a2=a2-a1=1+3d,所以由d=1+3d得d=-1/2.

因为a1=3d/2,所以,a1=-3/4.

所以存在a1=-3/4,使{an}成等差数列.

二、等价转化法

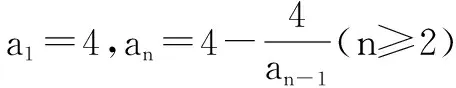
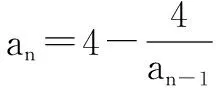
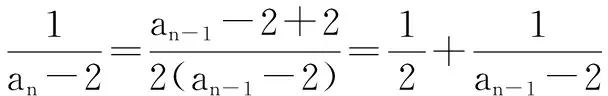
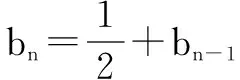
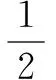
三、分离参数法

分离参数法在数列中参数值的解题方法中，主要是通过将主变量及参数混合在一起的形式，实现了对参数的分离，要求学生掌握不等式恒成立问题，并将恒成立问题作为解决函数最值问题的主要处理方法.

例3 已知数列{an}的各项均不等于零,且an=

由于{an}各项均不为零,此式两边取倒数得

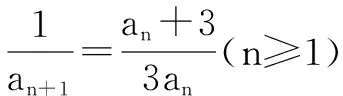
即{bn}(n≥1)是公差为1/3的等差数列.

四、逐段讨论法

逐段讨论法在数列参数值的解题中，主要是针对参数难以分离或者分离后最值不易求的问题进行分析和讨论的过程，该种解题方法主要是运用逐段筛选法的形式进行解题，解题时需要通过一系列的解题过程，对所要阐述的问题进行论证，对于不成立的部分，可以采用反向论证的方法来实现，将参数设置在一定的范围内.

例4 已知函数f(x)=x2-1(x≥1)的图象是C1，函数y=g(x)的图象C2与C1关于直线y=x对称.

(1)求函数y=g(x)的解析式及定义域M；

(2)对于函数y=h(x)，如果存在一个正的常数a，使得定义域A内的任意两个不等的值x1，x2都有|h(x1)-h(x2)|≤a|x1-x2|成立，则称函数y=h(x)为A的利普希茨I类函数.试证明：y=g(x)是M上的利普希茨I类函数；

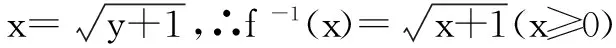
(2)对任意的x1，x2∈M，且x1≠x2，则有x1-x2≠0，x1≥0，x2≥0.

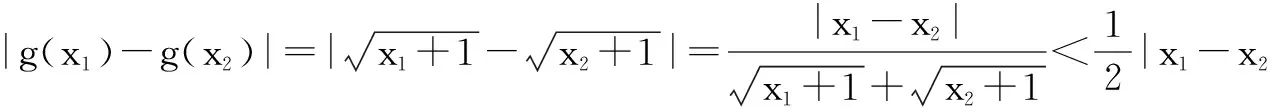
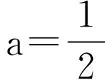
本文列举了一些数列中参数值具体的解题方法，并对每种解题方法中的一些典型例题进行了深入的分析，教会学生主要的解题方法，使学生的解题思路更加明晰，快速地掌握该部分的知识点，提高了解题的效率及准确率，提升学生的数学学习成绩.

[1]樊爱平. 如何确定数列中合适的参数值是否存在[J]. 新高考(高三数学),2012(01):31-32+54.

[2]何佳庆. 数列中参数值的确定方法探讨[J]. 高中数理化,2016(Z2):9.

[3]杨学枝. 用数学归纳法证明数列不等式得到的启示[J]. 数学通报,2015(06):59-63.

[责任编辑：杨惠民]

2017-05-01

艾菊梅(1982.10- )，女，江西抚州，中学一级，本科，从事高中数学教学.

G632

B

1008-0333(2017)16-0029-02