基于NMF的老电影音频背景噪声修复算法

张叶君,杨卫英

(上海大学上海电影学院,上海 200072)

基于NMF的老电影音频背景噪声修复算法

张叶君,杨卫英

(上海大学上海电影学院,上海 200072)

老电影音频资料经过长时间的存储会出现音频纯度低、存在噪声等问题.利用非负矩阵分解(non-negative matrix factorization,NMF)算法对单声道音频中的背景噪声进行自动、快速检测和分离以去噪.对非噪声和噪声信号分别建立相应的模型,即前者使用正弦模型;后者的模型通过对老电影中先验噪声信号进行训练得到,然后使用一种条件受限的NMF算法对音频中的背景噪声进行分离.实验结果表明,该算法在去噪效果上要优于直接滤波等去噪算法.

非负矩阵分解;音频去噪;盲源分离;噪声模型训练

“老电影”主要指影像制作过程中使用传统的光化学或物理处理技术,以胶片为存储介质的电影,这些电影主要在20世纪进行制作和发行.由于胶片本身的特性,经过长年累月的存放,会出现不同程度的磨损、老化,使得老电影出现音频内容的缺失、音频中存在噪声、纯度低等问题[1].另外,早期录音技术、设备、环境等条件限制还导致了音质低劣问题.这些老电影显然无法满足现代影迷的观感,为了能让它们重返荧屏,胶片老电影的保存和修复也成为业界亟待解决的问题.

对于老电影音频噪声的修复,国际上没有通用的系统方法.绝大多数的修复流程是先利用胶转磁、磁片还音车等设备将胶片声音进行数字化处理和存储,然后导入音频工作站中进行人工修复[2].目前已有一些专业的商用软件和插件能提供音频的去噪、增强等功能,如iZotope系列、Sonnox系列,它们的核心去噪算法主要基于减谱法[3]、直接滤波(如卡尔曼滤波)[4]等方法.这些方法在检测噪声位置及设置参数时,还需要依靠人工作业,会耗费大量的人力、金钱和时间,另外业内还缺乏技术熟练的修复人员,不能满足海量的影像修复需求.

为了能自动、快速地检测和修复老电影中的音频噪声,本工作采用以下思路：音频噪声的修复也可理解为从声音信号中分离出噪声信号,因而可将此问题视为盲源分离情况[5].将输入信号看作非噪声信号和噪声信号的合成,然后利用技术手段对这两种信号进行分离,即可达到去噪的目的.

非负矩阵分解(non-negative matrix factorization,NMF)[6]是近年来在数据分析、图像处理、盲源分离、语音增强[7-9]等领域兴起的技术.NMF先将数据看成大矩阵,将其分解成两个维度较小的矩阵,其中分解得到的矩阵能保留事物的特征,甚至可发现隐藏的特征成分.另外,如果能用模型表述数据中的不同特征,那么还可以利用NMF对这些特征进行提取和分类.虽然NMF在声音修复方面尚无具体的应用,但已广泛用于音频的相关研究[10-12],特别是在非稳态噪声环境下的语音增强领域.已有研究工作表明,要将NMF运用于特定的环境中,关键是需要根据待处理数据的类型构建合适的模型,模型可以是数学公式,也可以是通过样本训练获取的模型.

本工作在NMF算法的基础上加以扩充,提出如图1所示的老电影音频噪声修复流程,主要有以下两方面的创新.

图1 基于NMF的老电影音频背景噪声修复流程Fig.1 Flow chart of NMF-based historical film audio background noise reduction

(1)提出将NMF应用到电影原音的噪声修复中.已有噪声修复研究使用的原始样本是由不含噪声的纯音频信号通过人工加噪得到带噪信号,再利用NMF进行去噪.而本工作待处理的原始样本是老电影中的音频,本身便带有噪声.

(2)对老电影音频中的非噪声和噪声信号构建不同的信号模型加以区分.前者采用正弦模型,后者通过先验噪声样本训练得到,然后使用一种条件受限的NMF(constrained non-negative matrix factorization,CNMF)算法分离出其中的噪声.

1 NMF算法

NMF是将一个非负矩阵V分解为两个维度更低的非负矩阵W和H,即V≈WH,其v为列向量.同理,W和H也可以分别用列向量w和h来表达,分解公式可以写成等于W的每一列乘上hj中对应元素后的总和.一般将W称为基矩阵或特征矩阵,将H称为系数矩阵或增益矩阵.NMF算法试图将高维数据压缩成低维数据,并保留原始数据的特征,亦可以抽取其中隐藏的局部特征.不过,构造出良好的基矩阵W是关键.

在NMF算法[13]中,首先随机初始化W和H.为了保证分解前后数据的完整性,要使W和H的乘积尽可能接近V.通过设置迭代公式,对W和H进行迭代更新,同时还需要选取代价函数来测量V和WH的相似度,当代价函数小于某个阈值时,停止迭代,输出更新后的W和H.一般代价函数选择KL散度(Kullback-Leibler divergence)来测量二者的相似度：

为了不断减小D(V∥WH)的值,可对初始的W和H利用以下乘性更新法则进行迭代直至收敛：

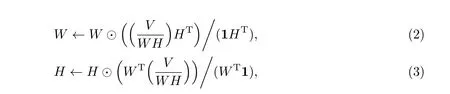
式中,Hadamard积⊙和除运算定义为两个矩阵对应元素的乘和除,1为元素全为1的矩阵.不过NMF算法只解决了如何对W和H进行迭代更新,使得WH能不断逼近V,并未涉及如何提取具有不同特征的局部数据.

一般电影声音中的非噪声大致可以分为对白、背景音乐和音效三部分.对白,即人物间的对话,可视为语音信号;背景音乐主要是通过不同音色的乐器演奏得到;至于音效,其种类五花八门,如碰撞声、拟声、摩擦声等.这些声音虽然发声方式不同,但均可看成是由一系列的正弦分量叠加得到.

而声音中存在的噪声大多不能转换成稳定的振动,或者是在自然界中不能表示为正弦形式的能量成分.因而可将声音信号x(t)看作非噪声信号s(t)和噪声信号n(t)叠加的模型[14]：

为了能将NMF算法用于老电影音频中非噪声和噪声信号的分离(见图2),需要分别对非噪声和噪声构造不同的模型.

图2 NMF分离非噪声矩阵Ws,Hs和噪声矩阵Wn,Hn示意图Fig.2 Diagram of separating harmonic matrix Ws,Hsfrom noise matrix Wn,Hnusing NMF

2 将NMF算法用于音频噪声修复

2.1 老电影声音信号基矩阵模型

2.1.1 非噪声信号的正弦模型

非噪声信号s(t)在时间域上可以近似表示为任意不同幅度、频率和相位的正弦信号之和[15]：

式中,p表示第p个正弦分量(p级谐波),ap,fp,ϕp分别表示幅度、频率和相位.

利用上述正弦模型构建矩阵Ws∈,如图3所示.矩阵的第p列代表第p个正弦分量,矩阵的维度N则代表各个正弦分量对应的幅值,即列向量中的元素为每个正弦分量对应的N个采样点的幅值.经过短时傅里叶变换(short-time Fourier transform,STFT)取绝对值后,可得非噪声基矩阵

图3 非噪声和噪声基矩阵模型的构建Fig.3 Modeling of harmonic and noise basis matrix

2.1.2 噪声信号模型的训练

老电影音频中的噪声主要由胶片的脏点、划痕、颗粒等问题引起,若按持续时长来分,可将这些噪声分为短时噪声和背景噪声;若按噪声内容来分,可分为咔哒声、爆破声、嗡嗡声等.这些噪声大部分可视为白噪声和其他类型的随机噪声,并且服从一定的统计分布规律.对于随机信号,比起直接建立模型,利用先验的噪声样本进行训练效果会更好.要完整地得到老电影音频噪声的先验特征,需要建立噪声训练库,获取老电影中各类噪声的样本,然后利用NMF算法进行训练得到对应类型噪声的基矩阵.但现有的老电影样本中很少有纯噪声的音频片段,特别是对于一些短时噪声,往往伴随着对白或者音乐一起出现.因此本工作中噪声训练的对象暂且只考虑背景噪声这一类.

在影像的某些时间段,会存在没有对白、音乐,而只有背景噪声的情况.提取出这段时间的声音,每个样本大约3～5 s,作为纯噪声信号n(t)进行训练：首先,进行STFT,取绝对值后的幅度谱作为NMF的输入矩阵接下来,利用传统的NMF算法对进行处理,得到纯噪声的基矩阵

2.2 受限的声音信号基矩阵模型

不同的数据类型,如文本、图像、音视频等,具有不同的表达特征.若在构建信号模型时直接使用NMF算法,去噪时会滤掉一些非噪声成分.为了能够有效利用NMF算法对这些数据进行处理,需要根据数据的特点和处理的目的对NMF算法进行优化.Wang等[16]对改进、优化的NMF算法进行了归类,将其分为受限NMF、结构化NMF和广义NMF等.为了能更好地区分非噪声和噪声信号,本工作基于文献[17]的方法思路,通过构建受限的非噪声和噪声基矩阵(见图4),用于老电影音频噪声的修复.

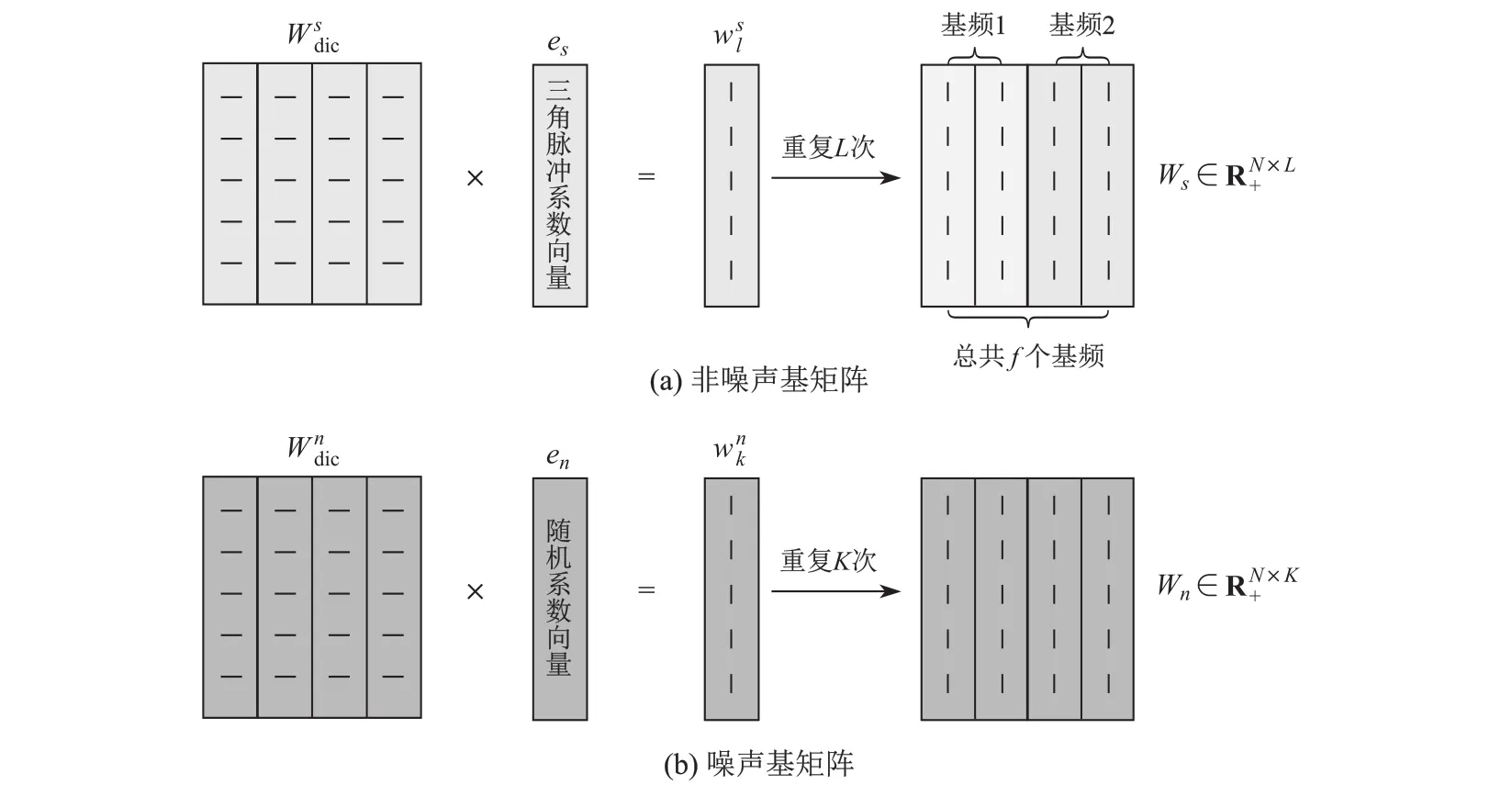
图4 非噪声和噪声受限基矩阵的模型构建Fig.4 Modelling of harmonic and noise constrained basis matrix

2.2.1 CNMF中非噪声基矩阵的构建

假设CNMF中受限的非噪声基矩阵Ws有L列,其中包含f个基频,每个基频有n列,那么L=fn.接下来对Ws中的原子进行构建,将2.1节中的非噪声基矩阵乘上三角脉冲信号向量es∈得到非噪声原子即受限的基矩阵Ws可以看成是原基矩阵与脉冲信号的线性组合.那么非噪声受限基矩阵Ws∈可以表示为

2.2.2 CNMF中噪声基矩阵的构建

假设CNMF中受限的噪声基矩阵Wn有K列,将2.1节中的噪声基矩阵乘上一个随机系数向量en∈,得到噪声原子∈.那么噪声受限基矩阵Wn∈可以表示为

2.3 基于CNMF的噪声分离

将构建好的受限基矩阵Ws和Wn组合为混合基矩阵的原子w可以表示为

利用式(8)初始化W,并随机初始化H(见图5).利用代价函数(9)度量相似度,利用式(10)和(11)分别对H和W进行迭代更新.

图5 CNMF中W和H的初始化Fig.5 Initialization of W and H matrix in CNMF

3 去噪实验

实验中待修复的老电影音频样本从上海电影技术厂获得.音频格式为WAV,采样频率为44.1 kHz,单声道.实验平台为Matlab R2016a.选取一些长10 s左右的音频片段,音频的主要内容为非噪声部分(包括乐器音效、人物间的对白、音乐等)、局部的颗粒声以及始终存在的背景嗡嗡声.然后,分别用本工作提出的算法和人工去噪插件进行噪声修复,并利用波形幅度分布分析信噪比(waveform amplitude distribution analysis signal-to-noise ratio, WADA-SNR)[18]作为客观评价指标进行对比分析.选取iZotope RX2和Sonnox Oxford这两款影视行业常用的噪声修复插件,其核心去噪算法分别基于减谱法和直接滤波法.

3.1 基于CNMF的去噪实验过程

步骤1选取一段带噪声的音频信号x(t),经过STFT取绝对值后获取幅度谱V∈在STFT过程中,帧长(汉宁窗长)为1 024个样本,帧移为25%的帧长.

步骤2利用CNMF算法分离噪声.收敛后提取出非噪声基矩阵和系数矩阵,相乘得到去噪的幅度谱Vs∈

CNMF算法中一些实验参数的设置如下：纯噪声样本训练中,噪声的基矩阵M取32,受限噪声基矩阵的原子长度K取 32;构建的受限非噪声基矩阵模型的正弦分量P取30,基频范围为40～400 Hz,梯度为10 Hz,即非噪声模型的基频有40,50,…,400 Hz,每个基频的原子长度n为8.

步骤3去噪后的幅度谱经过维纳滤波和逆短时傅里变换(inverse STFT,ISTFT),得到去噪信号s(t)及频谱图.在听感上,令人厌烦的背景嗡嗡声已去除.

3.2 实验结果比较与分析

仍然采用上述音频信号x(t),利用两种去噪插件进行去噪,得到的去噪前后的频谱图如图6所示.实验结果表明,即使在专业人员的指导下最大限度地发挥去噪插件的功能,也只能滤掉一部分噪声,在听感上从头到尾仍能感受到背景底噪声.而采用本工作提出的CNMF算法,对老电影中的背景噪声进行了较好的分离,修复效果要优于去噪插件所使用的减谱法和直接滤波法.从频谱图也可看到,采用CNMF算法的噪声能量得到了更为明显的衰减.

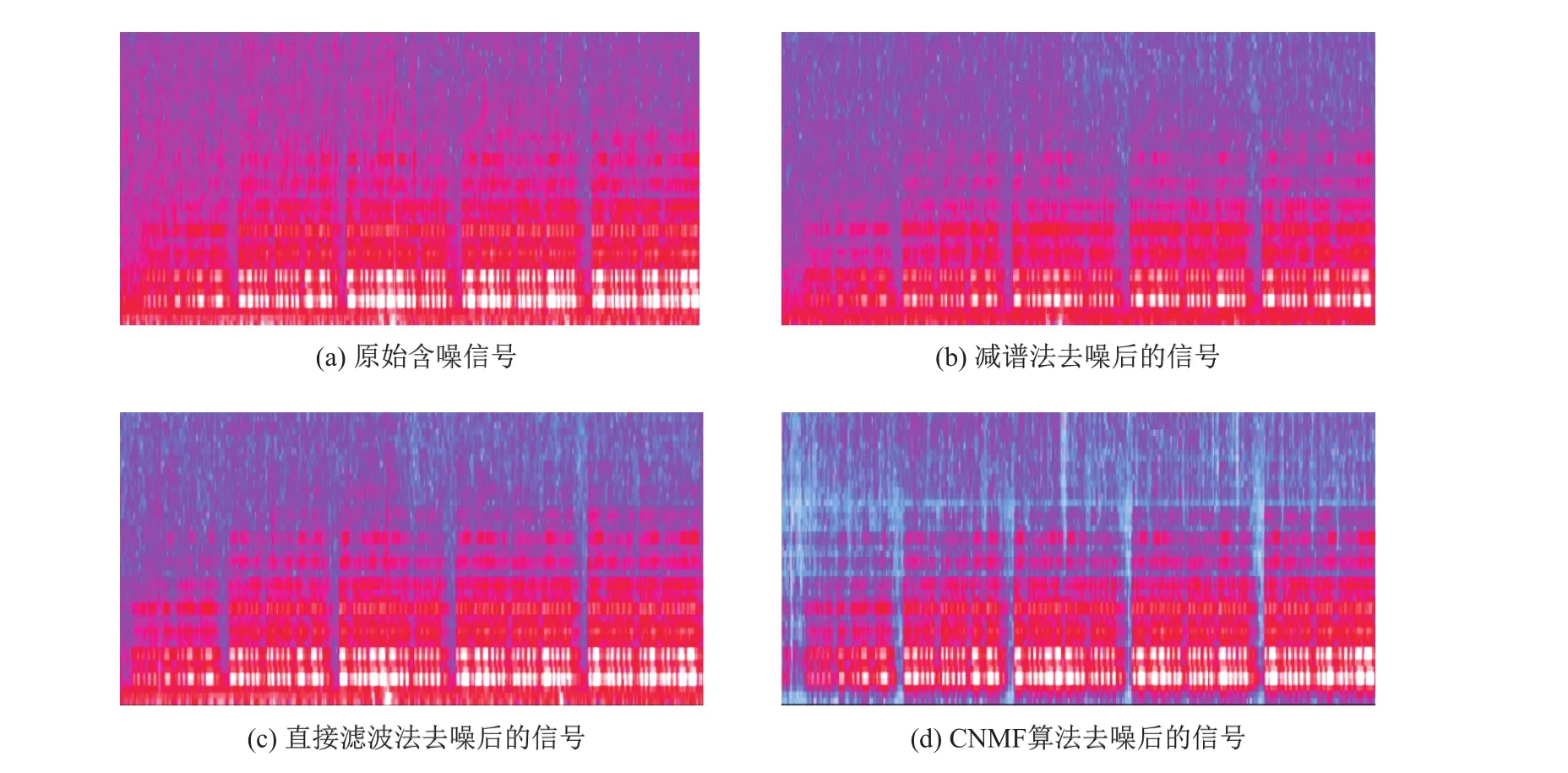
图6 不同算法修复结果频谱对比Fig.6 Comparisons of spectrogram using different reduction algorithms

接下来,选取12段不同内容的含噪音频片段,每段时长10 s左右,其中4段只含有对白元素,4段只含有音乐元素,另外4段同时含有对白和音乐.然后,分别用上述3种去噪方法进行处理,并使用一种改进的信噪比度量方法WADA-SNR作为评价指标进行比较.WADA-SNR的值越大,则表明音频质量越高,最大值为100 dB,实验结果如表1所示.实验数据表明：利用CNMF算法修复后的音频质量更佳.

另外,去噪插件在分离噪声的同时,也会滤掉少部分有用的非噪声信号能量,尤其是减谱法,从频谱图中可以看到原始非噪声的低频成分遭到了破坏.在本工作提出的CNMF算法中若不对NMF算法增加限制条件,去噪时会将少部分的高频非噪声成分视为噪声进行分离,导致音频出现轻微的削波现象.而增加受限条件的CNMF算法则能够在分离噪声的同时,更好地保留非噪声信号的成分.也就是说,对NMF算法进行优化,可提高噪声分离的准确性.

表1 不同噪声修复方法WADA-SNR指标的对比Table 1 Comparisons of WADA-SNR using different noise restoration methodsdB

4 结束语

针对大量老电影音频资料经长期存放濒临损毁的问题,本工作提出一种基于NMF的算法对老电影音频中存在的背景噪声进行修复.主要贡献有：①将NMF算法应用于老电影原音的噪声修复中;②分别构建了非噪声和噪声信号模型,前者利用正弦模型,后者通过对先验噪声信号的训练得到,再利用CNMF算法对老电影音频中存在的背景噪声进行分离.实验结果表明：所提出算法在去噪效果上要优于减谱法和直接滤波法.

虽然本工作提出的算法用在非噪声成分较多,且在存在背景噪声的情况下效果较好,而对于音频中声音要素少、噪声多的片段,则修复效果一般.另外,由于噪声训练阶段主要使用的是背景噪声样本,因而对于短时间内突然出现的其他类型噪声如咔哒声,还不能很好地进行抑制.未来在信号模型的构建、噪声库的训练、NMF算法的优化、修复效果的客观评价指标等方面还有待进一步研究.

[1]Rumsey F.Challenges in archiving and restoration[J].Journal of the Audio Engineering Society, 2016,64(1)：94-97.

[2]Napieralska J.Concept of film sound restoration by adapting to contemporary cinema theatre[C]//138th Audio Engineering Society Convention.2015：1031-1039.

[3]Lukin A,Todd J.Suppression of musical noise artifacts in audio noise reduction by adaptive 2-D filtering[C]//123rd Audio Engineering Society Convention 123.Audio Engineering Society. 2007.

[4]Grancharov V,Samuelsson J,Kleijn B.On causal algorithms for speech enhancement[J]. IEEE Transactions on Audio Speech&Language Processing,2006,14(3)：764-773.

[5]Belouchrani A,Abed-Meraim K,Cardoso J F,et al.A blind source separation techinique based on second order statistics[J].IEEE Transactions on Signal Processing,1997,45(2)：434-444.

[6]Lee D D,Seung H S.Learning the parts of objects by non-negative matrix factorization[J]. Nature,1999,401(6755)：788-791.

[7]Gillis N.The why and how of nonnegative matrix factorization[J].Regularization,Optimization,Kernels,and Support Vector Machines,2014,12：257-291.

[8]Weninger F,Roux J L,Hershey J R,et al.Discriminative NMF and its application to single-channel source separation[C]//15th Annual Conference of the International Speech Communication Association.2014：865-869.

[9]Zhou J,Chen S,Duan Z.Rotational reset strategy for online semi-supervised NMF-based speech enhancement for long recordings[C]//Applications of Signal Processing to Audio and Acoustics.2015：1-5.

[10]F´evotte C,Bertin N,Durrieu J.Nonnegative matrix factorization with the Itakura-Saito divergence：with application to music analysis[J].Neural Computation,2009,21(3)：793-830.

[11]Wilson K W,Raj B,Smaragdis P,et al.Speech denoising using nonnegative matrix factorization with priors[C]//IEEE International Conference on Acoustics,Speech and Signal Processing.2008：4029-4032.

[12]Papadopoulos P,Vaz C,Narayanan S S.Noise aware and combined noise models for speech denoising in unknown noise conditions[C]//17th Annual Conference of the International Speech Communication Association.2016：2866-2869.

[13]Lee D D.Algorithms for nonnegative matrix factorization[J].Advances in Neural Information Processing Systems,2001,13(6)：556-562.

[14]Serra X.Musical sound modeling with sinusoids plus noise[M].Amsterdam：Royal Swets& Zeitlinger,1997：91-122.

[15]McAulay R,Quatieri T.Speech analysis/synthesis based on a sinusoidal representation[J]. IEEE Transactions on Acoustics Speech&Signal Processing,1986,34(4)：744-754.

[16]Wang Y X,Zhang Y J.Nonnegative matrix factorization：a comprehensive review[J].IEEE Transactions on Knowledge&Data Engineering,2013,25(6)：1336-1353.

[17]Bertin N,Badeau R,Vincent E.Fast Bayesian NMF algorithms enforcing harmonicity and temporal continuity in polyphonic music transcription[C]//IEEE Workshop on Applications of Signal Processing to Audio and Acoustics.2009：29-32.

[18]Kim C,Stern R M.Robust signal-to-noise ratio estimation based on waveform amplitude distribution analysis[C]//9th Annual Conference of the International Speech Communication Association.2008：2598-2601.

本文彩色版可登陆本刊网站查询：http：//www.journal.shu.edu.cn

Reduction of background audio noise for historical films based on non-negative matrix factorization

ZHANG Yejun,YANG Weiying
(Shanghai Film Academy,Shanghai University,Shanghai 200072,China)

Audio materials of numerous historical films suffer from low sound quality,noise and other problems after being archived for a long time.This paper proposes a method based on non-negative matrix factorization(NMF)to automatically detect and separate background noise in a single channel audio.Harmonic signals and noises are modeled and differentiated using a sinusoid model and a priori noise training model respectively. Background noise is separated from the input audio with a constrained NMF algorithm. Experiments show that the proposed denoising algorithm outperforms the current algorithms in the denoise plug-in.

non-negative matrix factorization;audio denoising;blind source separation; noise model training

TN 912.3

A

1007-2861(2017)03-0333-09

10.12066/j.issn.1007-2861.1940

2017-05-02

国家自然科学基金资助项目(61571282)

杨卫英(1957—),女,副教授,研究方向为数字媒体技术等.E-mail：yangweiying@staff.shu.edu.cn