弹塑性索和黏滞阻尼器系统用于斜拉桥横向减震分析

游 瀚， 管仲国

(同济大学 土木工程学院，上海 200092)

弹塑性索和黏滞阻尼器系统用于斜拉桥横向减震分析

游 瀚， 管仲国

(同济大学 土木工程学院，上海 200092)

旨在研究弹塑性索对与黏滞阻尼器组合减震系统用于大跨度斜拉桥横向抗震设计作用。依据Caltrans规范构建了弹塑性索对的非线性本构关系，基于永宁黄河大桥弹性索对与黏滞阻尼器组合减震系统设计，通过调增地震波幅值，使弹性索进入塑性状态并分析结构响应。研究结果表明：容许拉索进入塑性可以显著增加其变形能力，进而提高整个结构应对强震作用的能力；与塔梁固定的常规体系相比，引入弹塑性索与黏滞阻尼器组合体系可以大幅降低主塔塔底弯矩及主梁加速度响应；与理想弹性索对工况相比，采用弹塑性索对虽然会导致较大的主梁残余位移，但对于控制最大索力和改善主梁加速度响应效果明显，同时塔梁、墩梁最大相对位移和塔底弯矩基本不变。

斜拉桥；横向减震；弹塑性索；黏滞阻尼器

斜拉桥是大跨度桥梁常用桥型，具有良好的美观、力学和经济性能，应用日渐广泛。大跨斜拉桥一般为路网中的关键枢纽工程，建设周期长，投资规模大，一旦发生地震损坏，往往导致很大的直、间接经济损失，同时斜拉桥结构具有柔性大和低阻尼的特点，易受强震损害。为确保结构安全及使用性能良好，其灾害防护是工程研究中一项富有挑战性的工作[1-2]。

大量实践证明：采用减、隔震设计是一个经济合理的选择，可以实现结构地震内力与位移响应较好地平衡[3-5]。斜拉桥纵桥向一般采用全漂浮或半漂浮体系，并较多运用附加阻尼等以控制主梁位移[6-8]。但在横桥向，因抗风等正常使用性能要求，塔梁、墩梁横向应具备足够的刚度，常采用抗风支座。这种横向固定约束通常导致塔、墩、基础等的地震内力响应非常大。当地震作用较强，尤其当桥址为近断层、跨断层等极端强震发生区域，这种体系就很难满足要求。

目前，对大跨度桥梁的横向减震，一些学者也进行了一定研究探索。叶爱君等[9]基于苏通大桥分析了边墩与主梁三种横向约束体系：横向滑动、全限位和黏滞阻尼器减隔震体系，证明黏滞阻尼器可以有效减小边墩的横桥向内力以及梁端位移。冯云成等[10]基于厦漳跨海大桥南汊桥分析了塔梁设弹性索、及墩梁设黏滞阻尼器减震形式，发现对减小内力响应均有帮助。在工程应用方面，管仲国等[11]采用E型钢阻尼支座用于南京夹江大桥(独塔自锚式悬索桥)的墩梁横向减震设计(塔梁间横向仍为固定)；希腊Rion-Antirion桥[12]在塔梁、墩梁横桥向采用黏滞阻尼器和牺牲性连杆的减震保护系统，以适应强震作用及断层位移，但牺牲装置的构造较为复杂，同时其在地震中的拉断破坏对结构以及阻尼器的影响尚不明确。

对于斜拉桥的横向约束体系，从静力作用上考虑，需要具备足够的约束刚度；从强震作用上考虑，则需要足够的变形能力，以及必要的耗能作用。甘肃永宁黄河桥为8度场地混凝土主梁双塔斜拉桥。由于地震作用强、主梁质量大，塔梁、墩梁处均需采用纵、横向减震设计。最终，塔梁处的横向减震采用弹性索与黏滞阻尼器的组合方案[13]。该方案具有诸多优点：①弹性刚度与阻尼比任意可调，体系适应性较强；②弹性索最大弹性位移受有效索长控制(一般为有效索长0.8%)，最大出力受索丝强度和丝数控制，尤其适用于同时要求较大出力和位移需求的塔梁横向连接；③弹性索保持弹性工作，黏滞阻尼器为速度依赖性，因此结构自恢复能力强，震后无需修复或者复位；④采用成品斜拉索，故工作性能与耐久性能成熟可靠，连接构造简单，安装方便。但成品斜拉索的最大变形一般要求达到≥2%有效索长。由此可见，在罕遇地震条件下，只考虑索的弹性变形，并不能充分发挥索的效能，尤其当需要较大的索变形时，需要的索长也较长。若能利用其部分塑性参与结构耗能减震，则可达到更高的减震效能。

本文以甘肃永宁黄河桥为背景，考虑塔梁横向拉索在强震作用下进入塑性，分析其对结构地震响应的影响，进而评估弹塑性索与液体黏滞阻尼器并联的减震效能与可行性。

1 弹塑性索、黏滞阻尼器组合减震系统

1.1 基本构造

弹塑性索采用成品斜拉索，横向设置在主塔与主梁之间。由于拉索具有单向受拉的力学特点，需成对设置以满足正负方向上的对称约束行为，如图1所示。黏滞阻尼器两端采用球铰连接，以满足主梁纵向上的温度及地震位移需求。当然，塔梁纵向阻尼器也同样需要设置球铰连接，以满足主梁横向上的位移需求。

1.2 力学模型

目前仍缺乏足尺长索的弹塑性拉伸试验。考虑到拉索的变形主要由索丝的行为所决定，参照美国加州Caltrans规范[14]“3.2.4”中对1 725 MPa钢绞线的应力应变关系(式(1))来确定拉索的弹塑性本构：

(1)

式中：fps为索丝应力；εps为索丝应变。记弹塑性索有效索长为L；索丝数目为N。则拉索的屈服位移：Sy=0.007 6L；初始刚度：K1=EA/L，其中拉索面积A=πd2/4×N，弹性模量E=196.5 GPa；屈服力：Fy=K1Sy。

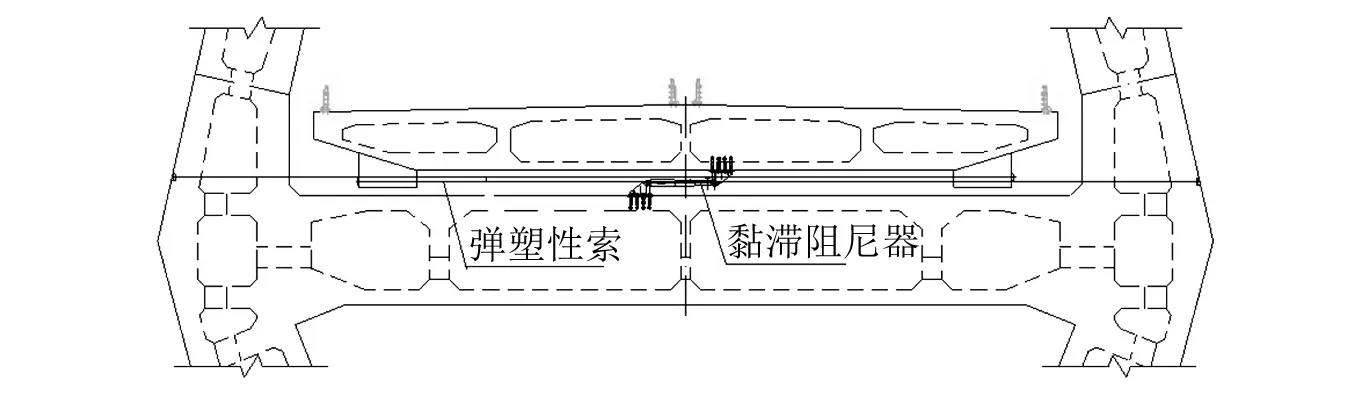
图1 减震装置构造Fig.1 Configuration of isolation devices

图2为索长33 m，索丝数121的OVMLZM7-121索(同永宁黄河桥弹性索)按Caltrans本构与按Wen模型拟合的对比。由图2可知，Wen模型总体上可以较好地模拟拉索的弹塑性本构，仅在近屈服点处产生一定的偏差。屈后刚度与初始刚度的比：K2/K1=0.015。在SAP2000中，单根弹塑性索可以用Wen单元与hook单元串联模拟(见图3)，Wen单元模拟双向弹塑性力学性能，hook单元实现单向传力。对于一组拉索对，其单元力学模型，如图4所示。同样由于拉索的单向受拉特点，索对的滞回关系不是平行四边形，而是呈理想的捏拢形态，如图4所示。

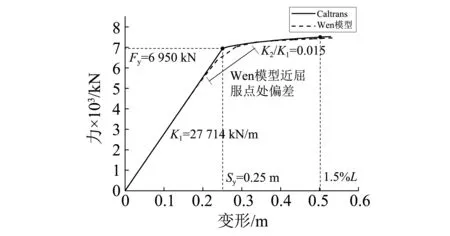
图2 索本构关系模拟Fig.2 Simulation of cable’s constitutive model

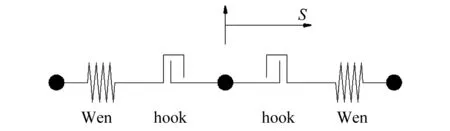
图3 弹塑性索单元图示Fig.3 Figure of elastoplastic cable element

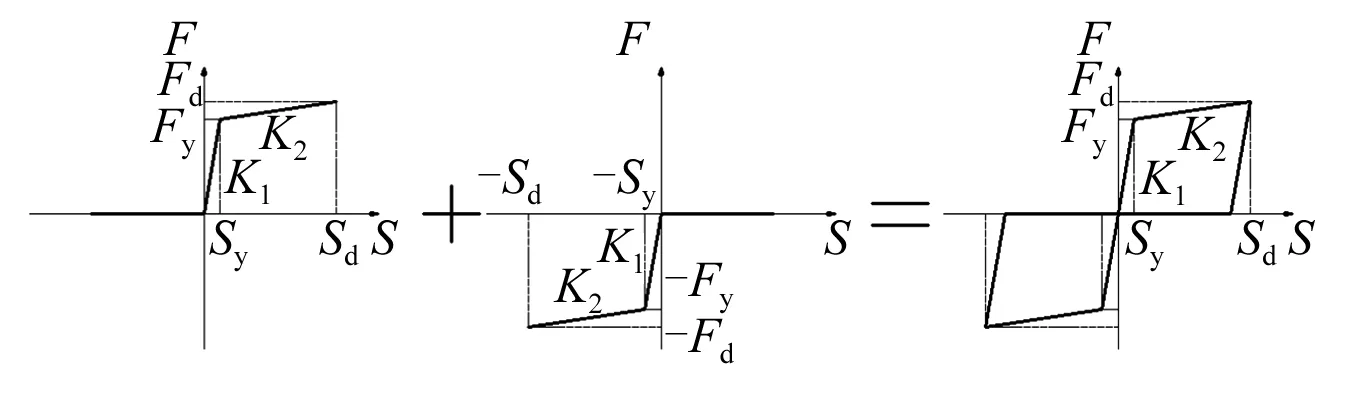
图4 弹塑性索力学模型Fig.4 Mechanical model for elastoplastic cable

黏滞阻尼器恢复力模型由下式表示。

F=CVα

(2)

式中：F为阻尼力；C为阻尼系数，主要与阻尼孔开孔面积有关；V为阻尼器运动相对速度；α为阻尼指数。本次研究中，黏滞阻尼器参数取永宁黄河桥相同的设计参数：C=2 500 kN·(s/m)0.3，α=0.3。弹塑性索与黏滞阻尼器横向设置在塔梁之间，为并联关系(见图5)。

图5 弹塑性索、黏滞阻尼器单元关系图示Fig.5 Element relation of elastoplastic cable and viscous damper

墩梁连接采用与永宁黄河桥相同的防屈曲约束支撑，属于钢阻尼器，其本构关系采用双线性模型模拟，在SAP2000中可用Wen单元。

2 减震效能实例分析

2.1 斜拉桥模型

选用永宁黄河大桥作为工程背景，主桥为110 m+260 m+110 m双塔双索面斜拉桥(见图6)。主梁采用变截面连续箱梁；主塔为钻石型混凝土塔；边墩采用柱式薄壁墩，且无辅助墩；基础全部采用钻孔灌注桩。在SAP2000中建立主桥弹性模型(见图7)，其中桥塔、桥墩、主梁、拉索均采用空间梁单元进行模拟。构件质量均采用集中质量，分配于单元端点。桥面二期恒载模拟为附加质量，分布于主梁各节点。主塔处基础要考虑冲刷作用，按高桩承台进行建模；而边墩不用考虑冲刷，直接用质点模拟承台，用六弹簧子结构模拟桩基础，土弹簧刚度通过m法获得。在主桥弹性模型上增加非线性连接单元用以模拟各种减震装置。主梁与中塔横向设置两对弹塑性索以及一个黏滞阻尼器；主梁与边墩横向设防屈曲约束支撑，模拟方式如“1”所述。结构动力特性计算结果，如表1和图8所示。

2.2 地震动输入

永宁黄河大桥桥址属于Ⅱ类场地，特征周期0.45 s，除了与设计谱匹配的3条人工场地波外，还从PEER的NGA数据库选取4条实际地震记录作为地震动输入(见表2)，并取7条波计算结果平均值作为最终结果。为了研究强震条件下减震索进入塑性后的影响，定义原永宁黄河桥罕遇地震输入为基本地震输入，即调幅系数1.0，其加速度反应谱，如图9所示。在此基础上，通过线性放大地震动的幅值，以实现更大强度的地震激励。

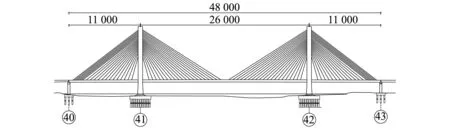
图6 斜拉桥总体布置Fig.6 Configuration of cable-stayed bridge

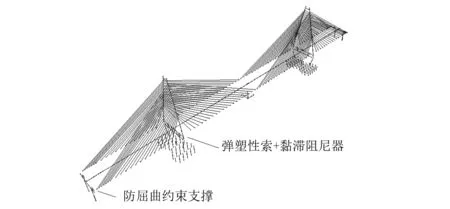
图7 斜拉桥有限元模型Fig.7 Finite element model for the cable-stayed bridge

模态阶数周期/s振型14.95主梁纵漂+竖向振动(反对称)23.57主梁横向振动(对称)33.04主梁横向振动(反对称)42.45主梁竖向振动(对称)

图8 斜拉桥前4阶振型Fig.8 First 4 vibration modes of cable-stayed bridge

编号地震名持时/s间隔Δt/s放大系数H_H-E05140ImperialValley-06250.0050.87FRE000LomaPrieta39.9450.0053.61BLD090Northridge-0139.980.022.07GAZ000Gazli,USSR16.260.0050.660.45-1人工波200.02-0.45-2人工波200.02-0.45-3人工波200.02-

图9 Tg=0.45 s地震动输入反应谱Fig.9 Response spectrum of seismic input with Tg=0.45 s

2.3 结构响应分析

将地震输入逐级放大，放大系数从1.0～1.8，使塔梁拉索对有较为充分的塑性发展。此外，另设置一对照工况，假定索不受屈服强度影响，可以始终保持弹性状态。

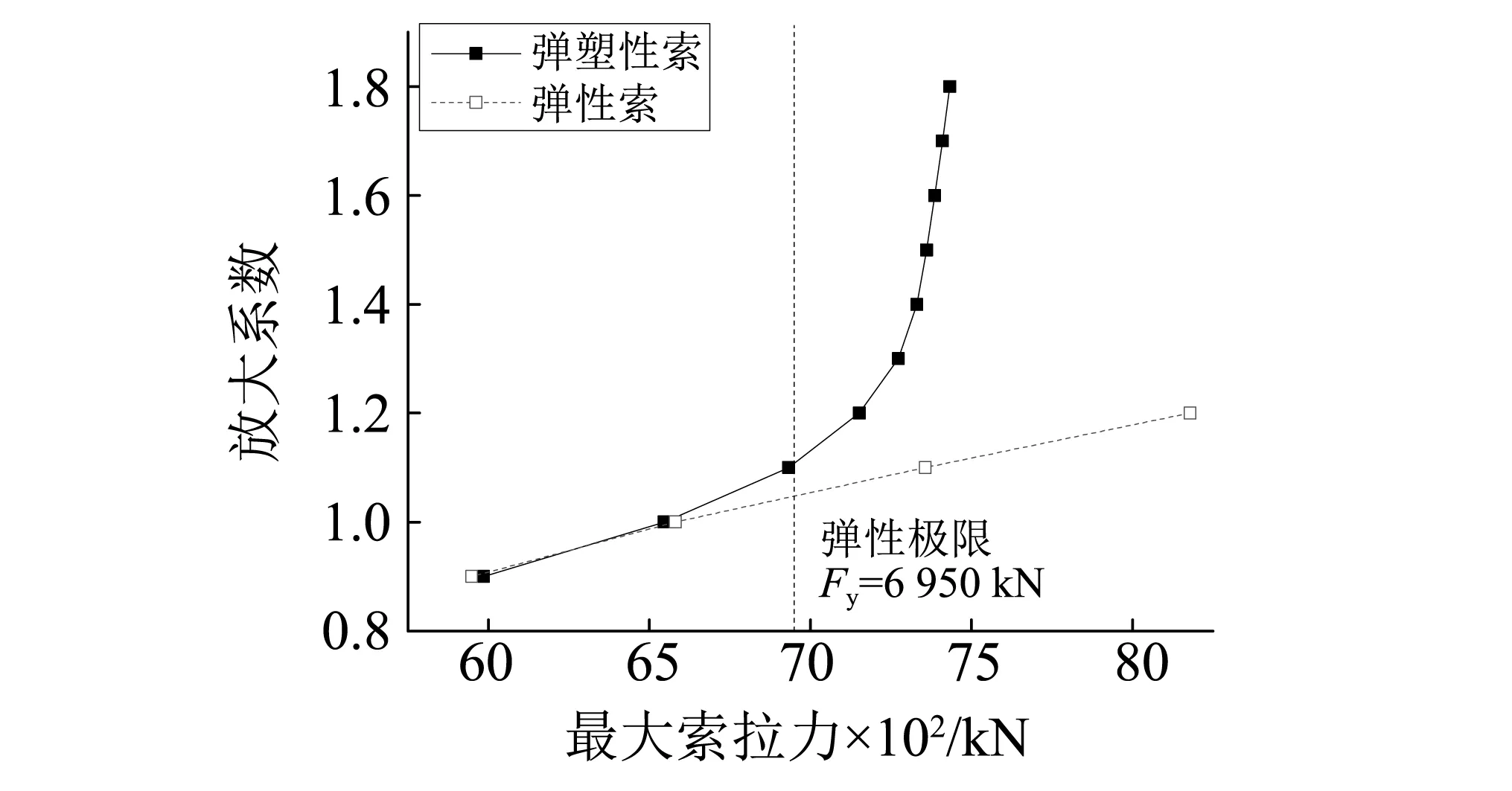
图10 最大索拉力响应Fig.10 Maximum response of cable force

图10所示为拉索对的最大拉力响应随地震输入增加的变化曲线。可以看出，对于弹塑性索对工况，当放大系数<1.2，索力增长速度较快；而当放大系数>1.2后，索力增长迅速下降，表明拉索已进入明显塑性状态。而对于理想的弹性索对工况，索力基本呈线性增加，且增幅较快。其中，两曲线在放大系数1.0至弹性极限之间发生分离是由Wen模型在本构关系近屈服点处的偏差所致(见图2)。由此可见，容许拉索进入塑性状态更有利于控制最大塔梁传力。

图11以GAZ000地震波作用为例，绘制了地震放大系数分别为1.0和1.8时塔梁横向拉索、黏滞阻尼器以及墩梁横向防屈曲约束支撑的力-位移曲线。可以看出，在1.0倍地震输入下，拉索变形<25 cm，处于弹性状态，阻尼器的变形也较小，耗能相对较少，梁墩防屈曲约束支撑已进入塑性。而当地震放大系数达到1.8倍时，拉索对呈现出明显的塑性滞回特性，并与理论模型(见图4)符合较好，塔梁黏滞阻尼器和墩梁防屈曲约束支撑也都因相对位移的明显增大而产生较多的耗能。

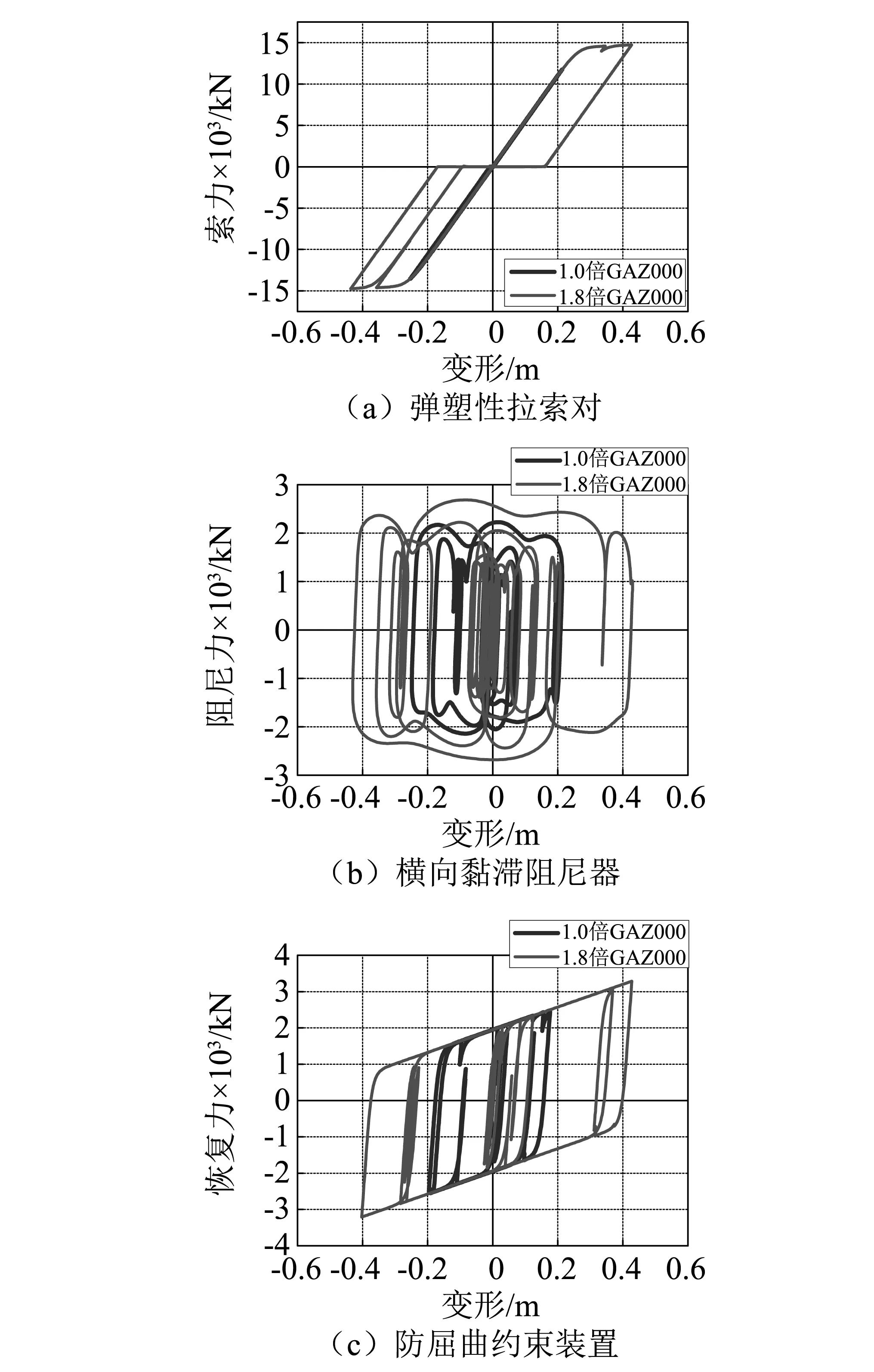
图11 不同地震输入下的减震装置力-位移曲线Fig.11 Force-displacement curve with different seismic input

图12所示为塔梁、墩梁相对位移需求。从图12可知，随着地震输入的增大，塔梁、墩梁相对位移基本呈线性增长状态，并没有因为拉索进入塑性状态导致塔梁相对位移需求的迅速增加，且弹塑性索与弹性索响应相差很小。这主要是因为塔梁横向采用弹性索约束，其周期可达3.57 s，位移响应主要受地震波等位移区段控制，因拉索进入塑性导致的周期进一步延长并不会对位移响应产生显著影响。其中，对应地震放大系数1.8时，弹塑性索对的最大变形(也即塔梁相对位移)约为0.5 m，合拉索最大应变1.5%，小于2.0%最低极限变形指标，表明此时拉索仍具有足够变形安全余度。需要指出的是，此应变响应已远超高强钢材的弹性应变，表明钢拉索实际上并不能满足理想的弹性工作假定。此外，对应地震放大系数1.8，墩梁相对位移需求也接近0.45 m，远超原设计防屈曲约束支撑的设计变形能力0.25 m。由此可见，容许拉索进入塑性，可以显著提高其变形能力，进而提高整个结构对强震作用的适应性，此时应将墩梁处阻尼器同样更换为弹塑性索对与阻尼器组合。

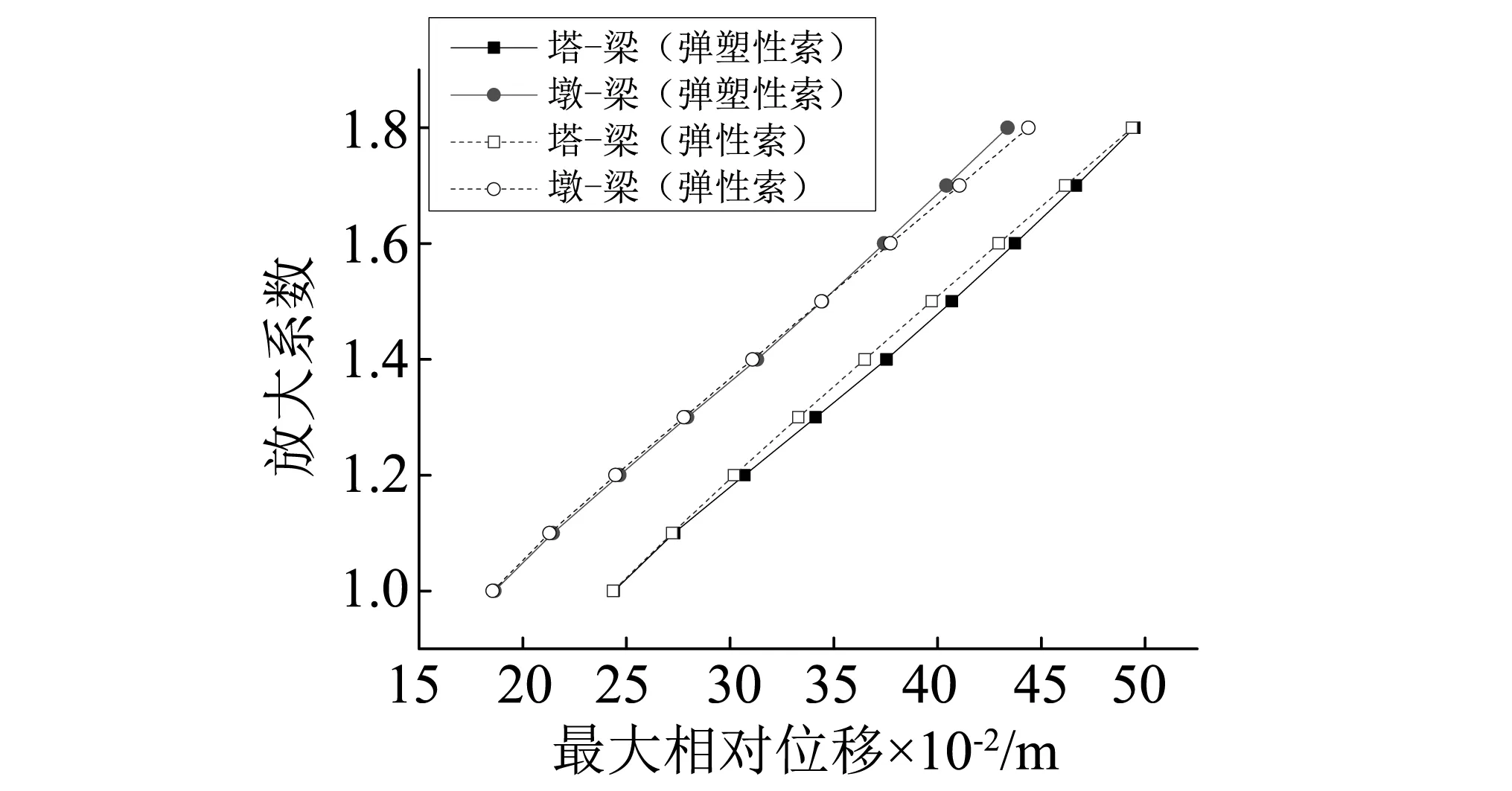
图12 最大相对位移响应Fig.12 Maximum relative displacement response

主梁残余位移，如图13所示。从图13可知，弹塑性索工况的主梁残余位移要明显高于理想的弹性索工况。但总体上两种工况下的残余位移幅值都较小，最大残余位移仅为约4 cm。究其原因，一方面，斜拉桥主梁为悬吊结构，拉索的重力刚度有助于减小震后斜拉桥的残余位移；另一方面也应指出，数值模拟中塔、梁、基础等均按弹性模拟，地震输入也未考虑空间效应和永存地表位移，因而所计算的残余位移会偏小。同时从图13还可知，在各级地震输入下，塔梁处的残余位移总小于墩梁处，表明拉索对与黏滞阻尼器组合比钢阻尼器具有更好的自恢复性能。事实上，对应1.0地震放大系数，索对保持弹性，黏滞阻尼器为速度依赖性，理论上可以在震后完全复位，之所以有残余位移主要是因为墩梁处的残余位移以及主梁的横向约束刚度；对应1.8的地震放大系数，对比图11(a)和图11(c)即可知，弹塑性索对的最大变形中，60%为弹性变形，而防屈曲约束支撑则仅有5%为弹性变形。

图13 残余位移Fig.13 Residual displacement

随着基于性能的抗震设计理论研究地不断深入，越来越多的研究也注意到结构的加速度响应对附属设施等非结构构件以及人员、行车等的安全性的影响。对于公路桥梁结构，目前还没有有关加速度限值的明确规定。但对隔震建筑，有研究建议楼层最大加速度宜<3 m/s2[15]。由图14可知，采用横向减震措施后，对应各级地震强度，主梁加速度响应均<3 m/s2，其中弹塑性索工况对于控制主梁加速度响应效果更好，而按塔梁固结方式则均>3 m/s2。

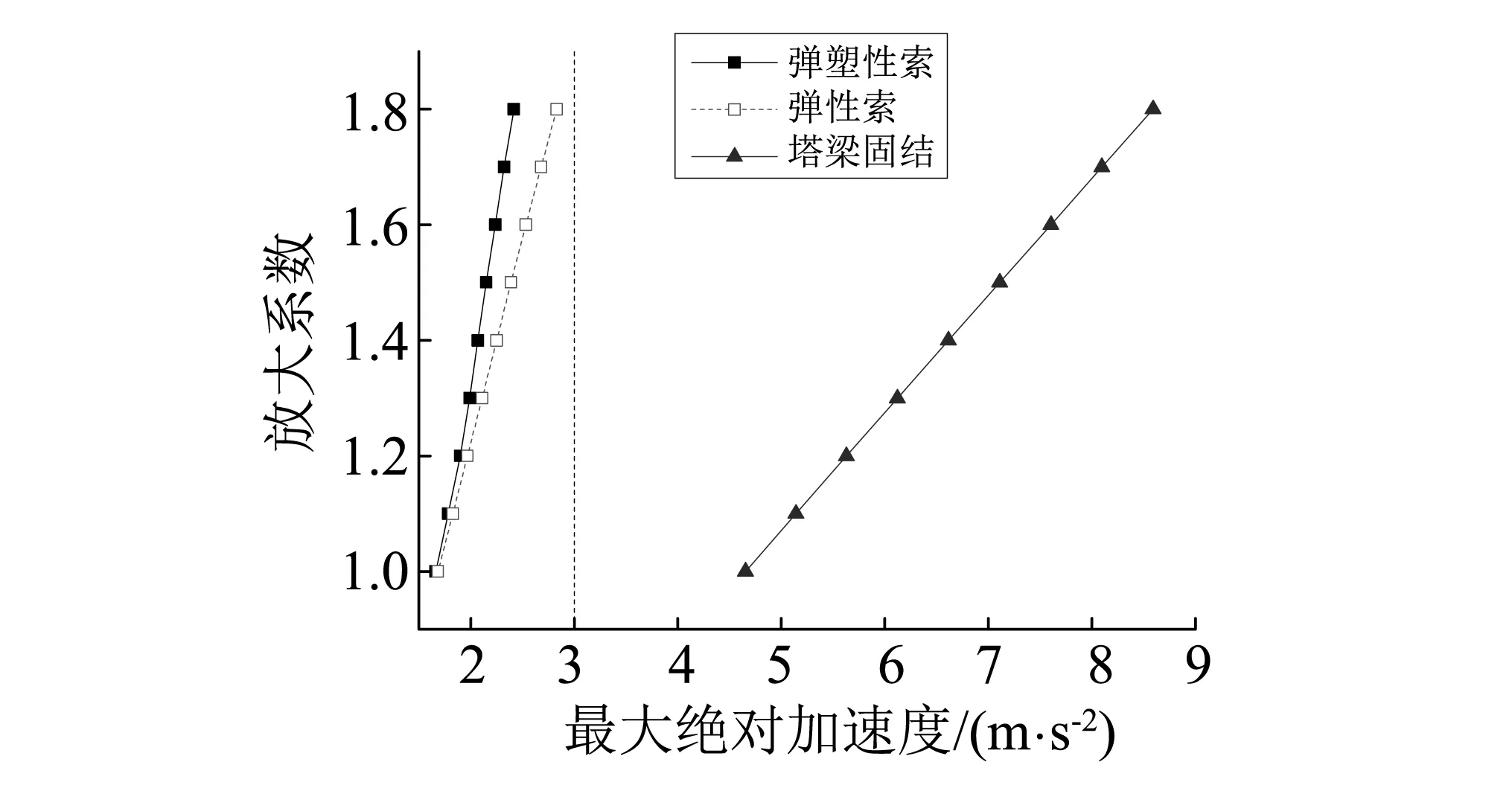
图14 主梁最大绝对加速度Fig.14 Maximum absolute acceleration of main girder

对于主塔，通过绘制各级地震作用下塔底内力(见图15)，可以看出采用减震措施后主梁的最大塔底弯矩与塔梁固结相比显著降低(减小40%以上)，且塔底弯矩随地震增幅的增长速度也明显小于塔梁固结情况。采用减震设计后，当地震放大至1.7倍时，塔底弯矩才与塔梁固结状况对应1.0倍地震作用时的响应基本相当。此外，从能力需求比曲线可看出，塔梁固结下的各工况能需比均<1，采用减震装置后，地震放大<1.6倍时，能需比均>1。由此可见，在采用弹塑性索与阻尼器组合减震体系以后，即使考虑地震作用的随机性，仍可在很大程度上保证主塔处于弹性工作状态。相比弹塑性索和弹性索工况，两者在塔底弯矩响应上的差异很小，这主要是因为当采用减震措施后，塔梁横向作用力已得到显著降低，塔底弯矩已主要由塔自身的惯性力控制。

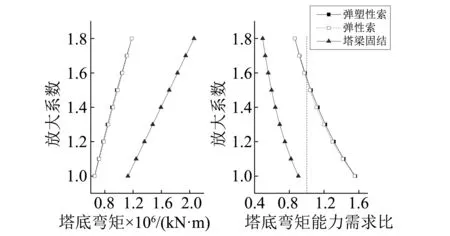
图15 塔底弯矩响应Fig.15 Moment response at bottom pylon

3 结 论

本文基于永宁黄河桥，建立有限元模型，分析了弹塑性索、黏滞阻尼器减震系统用于斜拉桥主塔横桥向减震的适用性，并得出了一些有益的结论。

(1)容许拉索对进入塑性可以显著提高其变形能力，进而提高整个结构应对强震作用的能力，偏于安全地考虑1.5%的拉索最大变形，原按弹性设计的地震作用放大至1.8倍，塔梁相对位移需求仍可满足。

(2)与塔梁固定的常规体系相比，当地震放大增至1.7倍时，塔底弯矩与塔梁固结状况对应1.0倍地震作用时的响应基本相当，主梁的绝对加速度响应可控制在<3.0 m/s2的水平。

(3)与理想弹性索对工况相比，采用弹塑性索对尽管会导致相对较大的主梁残余位移，但对于控制最大索力和改善主梁加速度响应效果显著，同时塔梁、墩梁最大相对位移和塔底弯矩可基本保持不变。

(4)本文基于Caltrans规范建立弹塑性索对的本构模型，数值分析结果表明其可以较好地模拟弹塑性索对只受拉的力学特点以及各项非线性属性。建议进一步通过相关试验加以验证和完善。

[1] HA D H, PARK J H, PARK K S, et al. Optimization of complex dampers for the improvement of seismic performance of long-span bridges[J]. KSCE Journal of Civil Engineering. 2009,14(1):33-40.

[2] HE W L, AGRAWAL A K, MAHMOUD K. Control of seismically excited cable-stayed bridge using resetting semiactive stiffness dampers[J]. Journal of Bridge Engineering, 2001, 6(6): 376-384.

[3] KUNDE M C, JANGID R S. Seismic behavior of isolated bridges: A-state-of-the-art review[J]. Electronic Journal of Structural Engineering, 2003, 3(2): 140-169.

[4] PARK K S, KOH H M, SEO C W. Independent modal space fuzzy control of earthquake-excited structures[J]. Engineering Structures, 2004, 26(2): 279-289.

[5] SHARABASH A M, ANDRAWES B O. Application of shape memory alloy dampers in the seismic control of cable-stayed bridges[J]. Engineering Structures, 2009, 31(2): 607-616.

[6] 叶爱君, 范立础. 附加阻尼器对超大跨度斜拉桥的减震效果[J]. 同济大学学报(自然科学版), 2006, 34(7): 859-863. YE Aijun, FAN Lichu. Seismic response reduction oI a super-long-span cable-stayed bridge by adding dampers[J]. Journal of Tongji University(Natural Science), 2006, 34(7): 859-863.

[7] ALI H E M, ABDEL-GHAFFAR A M. Seismic passive control of cable-stayed bridges[J]. Shock and Vibration, 1995, 2(4): 259-272.

[8] 焦驰宇, 李建中, 彭天波. 塔梁连接方式对大跨斜拉桥地震反应的影响[J]. 振动与冲击, 2009, 28(10): 179-184. JIAO Chiyu, LI Jianzhong, PENG Tianbo. Effects oI different connecting styles between towers and deck on seismic responses of a long-span cable-stayed bridge[J]. Journal of Vibration and Shock, 2009,28(10):179-184.

[9] 叶爱君，范立础．超大跨度斜拉桥的横向约束体系[J]．中国公路学报，2007(2):63-67. YE Aijun, FAN Lichu. Lateral constraint systems for super-long-span cable-stayed bridge[J]. China Journal of Highway and Transport, 2007(2):63-67.

[10] 冯云成, 燕斌, 牟宗军. 弹性索和阻尼器对斜拉桥横向抗震性能的影响[J]. 工程抗震与加固改造, 2009, 31(4): 24-28. FENG Yuncheng, YAN Bin, MU Zongjun. Effects of elastic cables and dampers on lateral seismic performance of cable-stayed bridge[J]. Earthquake Resistant Engineering and Retrofitting, 2009, 31(4): 24-28.

[11] 管仲国, 李建中, 朱宇. 弹塑性阻尼支座用于自锚式悬索桥减震设计[J]. 同济大学学报(自然科学版), 2009, 37(1): 6-12. GUAN Zhongguo, LI Jianzhong, ZHU Yu. Elastic-plastic energy dissipating bearing for seismic design of self-anchored suspension bridge with single tower[J]. Journal of Tongji University(Natural Science), 2009, 37(1): 6-12.

[12] INFANTI S, PAPANIKOLAS P, BENZONI G, et al. Rion antirion bridge; design and full-scale testing of the seismic protection devices[C]∥Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver, 2004.

[13] GUAN Zhongguo, LI Xiaobo, LI Jianzhong. An innovative isolation system for lateral seismic control of a cable-stayed bridge with heavy deck[C]∥IABSE Conference. Geneva, 2015.

[14] CALTRANS S D C. Caltrans seismic design criteria version 1.7[S]. Sacramento：California Department of Transportation, 2013.

[15] MIZUNO H, IIBA M, YAMAGUCHI N, et al. Shaking table testing on earthquake resistance of medical equipments[R]. Building Research Institute, Ministry of Construction, 1986.

Elastoplastic cable pair and viscous damper used in the lateral seismic isolation of cable-stayed bridges

YOU Han, GUAN Zhongguo

(College of Civil Engineering, Tongji University, Shanghai 200092, China)

The feasibility of utilizing the elastoplastic cable pair and viscous damper in the seismic isolation of long span cable-stayed bridges was evaluated. A nonlinear constitutive model for the elastoplastic cable pair was developed based on the Caltrans standard. Through linearly increasing the excitation intensity, the responses of the Yongning Yellow River Bridge were analyzed, where the elastic cable pair and viscous damper were successfully applied in lateral seismic control, and the cable pairs were forced to enter into an inelastic phase. The results show that the deformation capacity of cable pairs can be greatly enhanced if certain plastic behavior is allowed and consequently the ability of the structure against strong earthquakes can be significantly improved. In comparison with the conventional system with fixed transverse girder-tower connections, the utilization of elastoplastic cable pair and viscous damper can substantially reduce the base bending moment response on pylon and the acceleration response of girder. When compared with the hypothetic case with ideal elastic cable pair, though the residual displacement of the girder is relatively larger, the maximum transmitted force of the cables and the acceleration of the girder can be well controlled, while the relative displacements at the tower and piers and the base bending moment on tower columns maintain almost unchanged.

cable-stayed bridge; lateral seismic reduction; elastoplastic cable; viscous damper

973课题(2013CB036302)；国家自然科学基金(51378384)

2015-11-02 修改稿收到日期： 2016-04-15

游瀚 男，硕士生，1992年生

管仲国 男，博士，副研究员，博士生导师，1976年生

U441+.3

A

10.13465/j.cnki.jvs.2017.14.029