多轴向与单轴向随机激励下结构动力学响应对比研究

贺光宗， 陈怀海， 孙建勇

(1. 山东理工大学 交通与车辆工程学院, 山东 淄博 255049； 2. 南京航空航天大学 航空宇航学院, 南京 210016；3. 中国航空综合技术研究所， 北京 100028)

多轴向与单轴向随机激励下结构动力学响应对比研究

贺光宗1,2， 陈怀海2， 孙建勇3

(1. 山东理工大学 交通与车辆工程学院, 山东 淄博 255049； 2. 南京航空航天大学 航空宇航学院, 南京 210016；3. 中国航空综合技术研究所， 北京 100028)

为了分析结构在多轴向与单轴向振动环境下疲劳失效行为存在的差异，从理论分析、数值仿真以及试验研究三个方面，对典型结构开展了多轴向与单轴向随机振动环境下动力学响应对比研究。研究结果表明：多轴向振动环境能够同时激发结构不同方向的模态振型，在三个轴向互不相关的振动环境下，结构的动力学响应为各个方向单轴向振动时引起的动力学响应的叠加；若各轴向载荷间存在相关性，则其相关性对结构动力学响应存在明显影响，且影响是有规律的。对以上结论产生的原因进行了分析研究，为两种工况下结构振动疲劳失效行为的研究奠定了基础。

动力学响应；多轴向随机振动；振动疲劳；模态振型

航空航天、车辆及机械等行业中的产品所处的振动环境一般是多轴向的，有的振动环境甚至呈现三轴向六自由度特征[1]。但由于试验技术和设备的限制，在早期的研究中无法实现多轴向振动激励，因此，在多轴向振动环境试验中，研究者提出在三个正交轴向依次进行单轴向振动试验的方式等效真实的多轴向振动环境[2]。在半个世纪的实践中，这种试验方式产生了很好的效果，暴露了大量产品的缺陷，提高了产品的振动可靠性，该试验方式目前仍在被广泛应用。近年来，随着科学技术的进步和研究的深入，此类方法的有效性受到了广泛的质疑，文献[3-4]研究指出产品虽然通过了单轴等效试验，却在实际的振动环境中发生了疲劳失效；Whiteman等[5-7]对简单试件和典型产品进行了单轴向与多轴向振动疲劳对比试验研究。文献[8]采用等效应力法计算了结构在两种振动环境下的疲劳损伤，都指出两种振动工况下结构的疲劳时间、失效位置存在差异。但是对于两种工况下结构疲劳失效行为差异原因的分析和研究却很少，为更好的评估传统单轴向等效振动试验的有效性，明确其不足产生的原因，对两种振动模式下结构疲劳失效行为差异的成因开展研究十分必要。

工程结构或机械零件在振动环境中长期服役而产生振动疲劳失效，其根本原因是失效部位长期承受常幅或变幅的应力循环作用，应力循环会或多或少的对结构造成疲劳损伤，研究表明结构共振引起的高水平应力循环对结构的损伤起主要作用[9-10]，当疲劳损伤积累超过疲劳失效的临界损伤时，就会造成结构的疲劳失效。结构在振动环境中产生的应力的大小，方向以及应力分布将直接决定结构疲劳寿命，裂纹产生或扩展的方向，因此，研究结构在不同振动环境下的疲劳失效行为，应首先从研究结动力学响应入手。在多轴向振动环境下结构的动力学研究方面，Füllekrug等[11]对多轴振动环境下航空构件的动力学响应进行了研究，得到了频域内和时域内结构与基础激励加速度之间的关系表达式。Füllekrug[12]通过多轴向振动台模拟了地震激励，研究了S形结构在多轴向振动激励下的模态识别问题。陈颖等[13]对典型结构在单、多轴向振动环境下的加速度响应进行了试验研究，指出了两种工况下结构加速度响应存在的差异。

本文从理论分析、数值仿真和试验验证三方面，研究了结构在单轴向和多轴向随机振动环境下的动力学响应。通过对不同工况下结构的加速度响应和应力响应的比较分析，研究结构动力学响应的差异，并分析差异产生的原因，得到载荷工况对结构动力学响应的影响规律。为多轴向与单轴向振动环境下结构疲劳失效行为分析提供了理论依据。

1 理论分析

1.1 基础激励下多自由度系统的动力学响应

刚性基础激励下，多自由度系统的动力学方程为

(1)

(2)

式中:R为影响系数矩阵或刚体模态矩阵，其元素Rij的物理意义为仅在刚性基础第i激励自由度施加单位加速度时，结构上第j自由度的加速度响应，w(t)为刚性基础的位移。

将式(2)代入式(1)得到

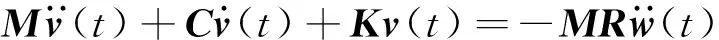
(3)

通过固有振型矩阵Φ=[φ1,φ2,…,φm]进行坐标变换，将物理坐标v(t)表示为

v(t)=Φη(t)

(4)

根据模态振型矩阵的正交性，式(3)可表示为

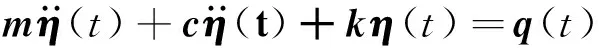
(5)

(6)

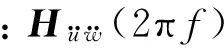
(7)

式中:A为对角矩阵，且

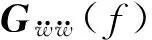
(8)

(9)

式中:Dσ为应力矩阵。

1.2 单、多轴向基础激励下动力学响应分析

由式(6)和式(8)可知，基础激励加速度与结构加速度以及应力之间的关系形式相同，在三轴向振动环境下可以表示为

(10)

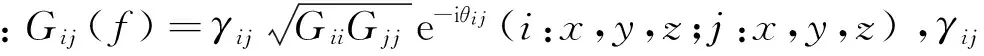
由上式可知，结构在三轴向振动环境中的响应包含了三个方向的加速度激励与不同方向的频响函数的组合。根据式(7)和式(9)可知不同方向的频响函数包含不同方向激励激发的模态振型，因此三轴向同时振动环境下的动力学响应包含了三个方向的模态信息。而结构在单轴向振动时式(10)简化为

(11)

式(11)中的动力学响应中只有本方向振动激发出的模态参与计算，因此多轴向同时振动与单轴向振动环境下结构的动力学响应在模态振型参与以及能量分布等方面都存在区别，差异的大小与各轴向载荷输入的量级以及各轴向载荷之间的相关性有关。下面首先考虑各轴向载荷互不相关的情形，即输入载荷谱间的互谱为零，则式(10)可以简化为

(12)

式中:Gx(f),Gy(f),Gz(f)分别为结构在各个方向单轴向振动工况下该点的动力响应的功率谱密度矩阵，由响应的均方根与响应功率谱密度矩阵之间的关系

(13)

得到结构在三轴向振动和单轴向振动环境下动力学响应的均方根值存在以下关系

(14)

由上式可知在三个方向互不相关的随机振动载荷作用下，结构上各点的响应为三个方向单独振动工况下引起响应的叠加，其量值应明显大于单轴向振动所引起的响应。另外，由于叠加作用，三轴向振动与单轴向振动环境下结构动力学响应的分布也是不同的。

根据式(10)，当考虑各轴向载荷间相关性时，随着输入载荷谱间的相干系数γij和相位角θij的变化，其互功率谱密度Gij(f)可能为正也可能为负，其量值也在不断变化，因此可能使得结构动力学响应增大，也可能削弱结构的动力学响应。各轴向载荷间相干系数和相位角的变化对结构的动力学响应的影响规律将在下文结构的动力学仿真中进行定量分析讨论。

2 典型构件动力学仿真分析

2.1 动力学仿真模型

本文动力学仿真和试验模型，如图1所示。结构在x，y，z方向的尺寸分别为180 mm，150 mm和120 mm，底板厚度10 mm，模型上方中央处有一边长为40 mm的正方体质量块，其余结构为横截面为5 mm×10 mm的矩形截面的板件。结构材料为铝合金6061-T6，弹性模量为69 GPa，泊松比为0.3，密度为2 700 kg/m3。采用大质量法模拟结构安装在振动台上产生的三轴向平动基础激励，通过模态分析得到结构的前三阶固有频率分别为122.14 Hz，186.52 Hz和214.13 Hz。模型前两阶振型为沿y轴向和x轴向的摆动，可分别由y轴向和x轴向的振动激发；第三阶固有振型为沿z轴向的垂直振动，可由z轴向振动的激发。

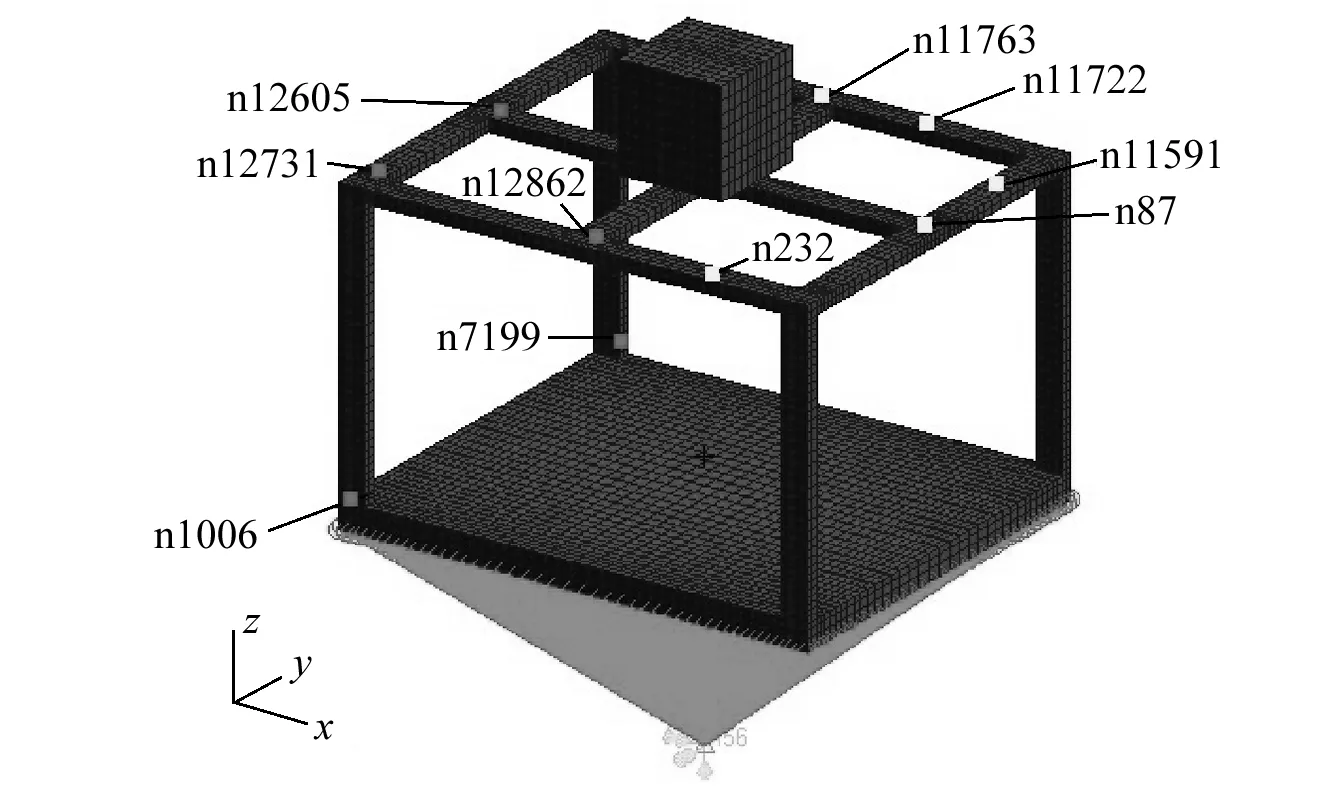
图1 结构有限元模型Fig.1 The finite element model

2.2 随机振动环境下动力学响应分析

对结构进行单轴向以及多轴向随机振动分析，载荷为施加在模型底板的加速度基础激励，根据模态分析的结果，三个方向的加速度激励的功率谱密度均采用量值为6×10-4g2/Hz的水平直线谱，载荷谱频带范围为100～250 Hz，加速度均方根为0.3g，分析过程中不考虑各轴向载荷间的相关性。

2.2.1 加速度分析

对结构进行三轴向与单轴向随机振动分析，分析节点,如图1所示。分析表明对于本文采用的结构x，y轴向的加速度响应主要由本方向激励所激发的模态计算得到，如图2为结构在三轴向和x轴向振动工况下x轴向的加速度响应，可见节点在两种振动工况下x轴向的加速度响应相同，说明三轴向振动时另外两个方向的模态在x轴向加速度响应的计算中的参与可以忽略不计。

(a)三轴向振动

(b)x轴向振动图2 典型节点不同工况下x轴向加速度PSDFig.2 The x-axial acceleration PSD of different load cases

但是结构上各节点在z轴向的加速度响应却与多个轴向的模态有关，如图3所示。当z轴向单独振动时z轴向加速度响应中只有第三阶模态被激发，而三轴向同时振动时z轴向加速度响应中有两个或三个轴向的模态被激发出来，说明三轴随机振动能够同时激发结构各个方向的模态振型，各节点z轴向的加速度均方根值也明显大于z轴向单独振动。

(a)三轴向振动

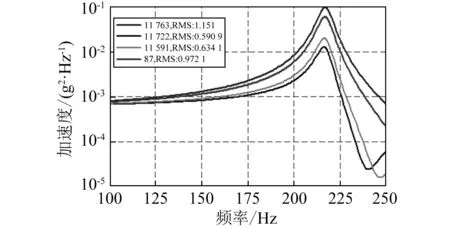
(b)z轴向振动图3 不同工况下z轴向加速度响应Fig.3 The z-axial acceleration PSD of different load cases

采用相同的激励，对结构在x和y轴向单独振动环境下进行了z轴向加速度分析。与图3中z轴单轴向振动相似，在x和y轴向单轴向振动时，结构各点的z轴向加速度功率谱密度在分析频带内只有一个峰值出现，结构的第二阶和第一阶模态分别被激发出来。各个节点在三个轴向单独振动以及同时振动时的加速度均方根,如表1所示。

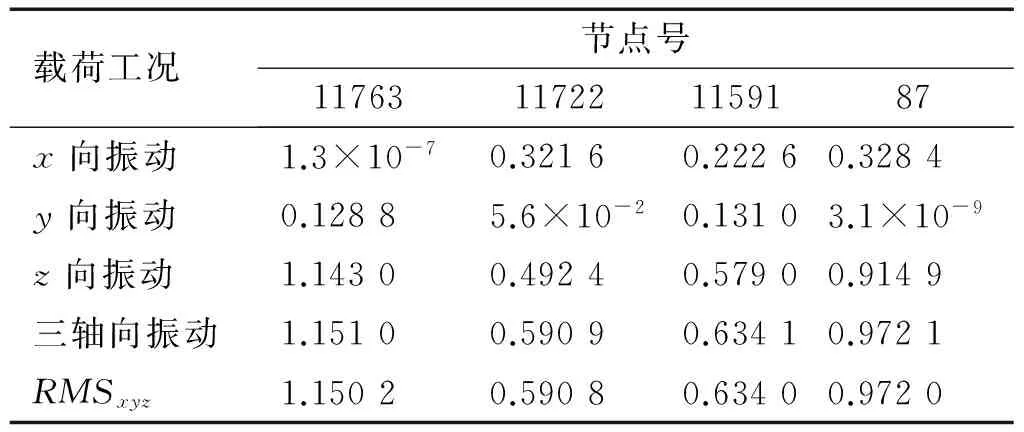
表1 不同工况下z轴向加速度RMS值

由表1可知结构三轴向振动工况下z轴向加速度RMS值与各轴向单独振动工况下z轴向加速度RMS值满足时式(14)。即当各轴向载荷谱互不相干时，三轴向同时振动工况下，结构在某个轴向的加速度响应为各个轴向单独振动工况下该轴向加速响应的叠加。

2.2.2 应力响应分析

对结构进行了三轴向与单轴向随机振动工况下应力响应分析研究。典型节点位置,如图1所示。分析发现与加速度响应不同，各节点的六个应力分量的功率谱密度图中均有三个峰值，例如y轴向正应力响应(图4)，即各应力分量计算中三个轴向的模态同时被激发出来，说明相比加速度响应(见图2)结构的应力响应的多轴效应更为明显。

图4 三轴向振动工况下节点y向正应力PSDFig.4 The y-axial normal stress PSD under 3-axial excitations

为了研究单轴向振动与三轴向振动环境下应力响应之间的关系，计算了三个轴向单独振动时与三轴向同时振动时各点的von Mises应力，其功率谱密度,如图5所示。可见在单轴向振动时结构的应力响应中只有本方向振动激发的模态参与，而三轴向同时振动时的应力中三个模态都被激发出来。

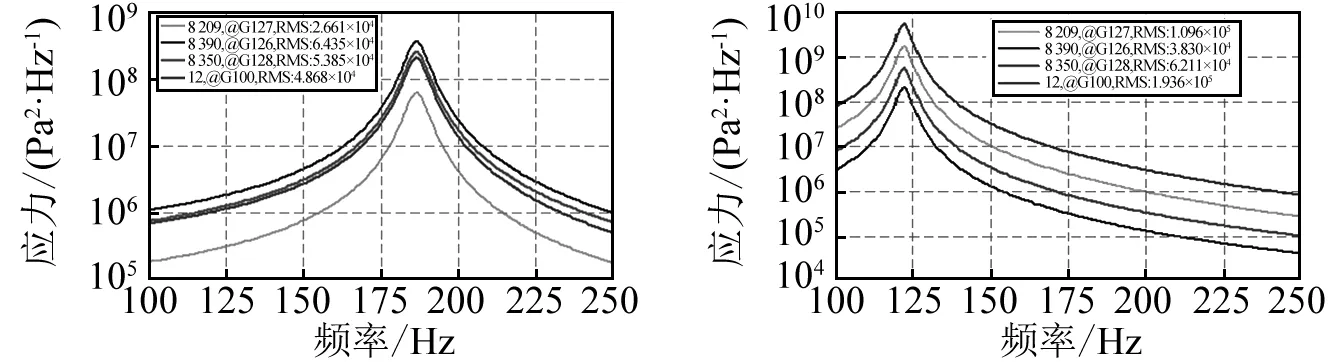
(a)x轴向振动 (b)y轴向振动

(c)z轴向振动 (d)三轴向振动图5 不同工况下von Mises 应力PSDFig.5 The PSD of von Mises stress of different load cases

各工况下节点的von Mises应力值,如表2所示，由数据可知在各轴向载荷谱之间互不相干的情况下，三轴向同时振动工况下在结构上某点引起的von Mises应力为各个轴向单独振动工况下在该点引起的von Mises应力的叠加，满足式(14)。

2.3 载荷相关性对动力学响应影响分析

对模型进行了x和y向同时振动试验，两个方向激励的自功率谱密度与前文三轴向振动试验相同。通过设置两振动方向载荷间不同相干系数和相位角的组合，得到不同耦合关系的两轴向同时振动环境，计算结构在不同振动环境下的动力学响应，研究载荷相关对结构动力学响应的影响规律。

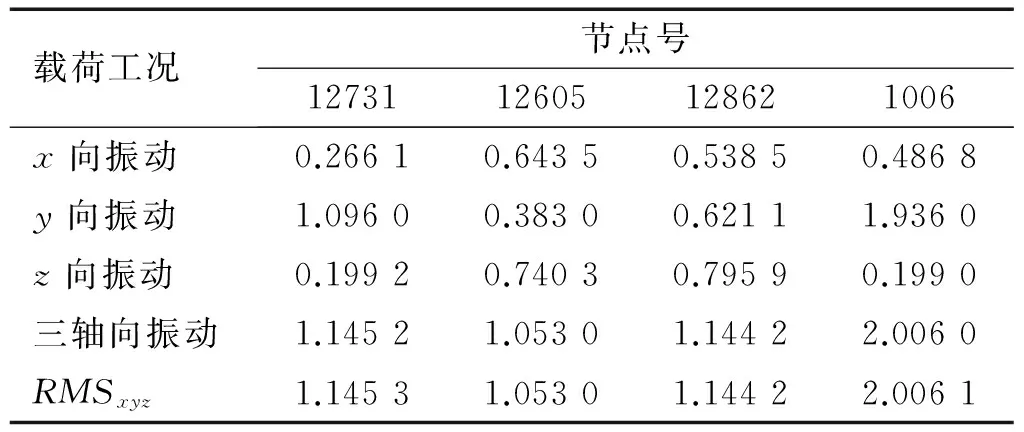
表2 不同工况下von Mises的RMS值

2.3.1 载荷相关性对加速度的影响

计算了典型节点在两个轴向不同相干系数与相位角组合工况下的z轴向加速度响应。结果表明：不同轴向载荷谱间相干系数和相位角的变化对结构z轴向加速的影响规律随着位置的不同而不同，87号节点和11763号节点(如图1所示，分别处于结构的x和y轴向对称轴上)，在两轴向载荷谱相干系数和相位角发生改变的情况下，其z轴向加速度并未放生变化，并且与两轴向载荷谱互不相干时的加速度值相同；其余节点z轴向加速度随相干系数和相位角改变的变化规律可以分为两种情况，如图6所示。由图6可知，z轴向加速度随两轴向载荷谱间相干系数和相位角的改变呈规律变化，如232号节点，当相位角小于180°时，z轴向加速度随着相干系数的增大而增大；当相位角>180°时，z轴向加速度随着相干系数的增大而减小。在相同相干系数工况下，z轴向加速度随相位角的增大呈先增大然后减小，再增大的类似正弦的变化规律，z轴向加速度的最大值和最小值分别出现在相位角为90°时以及270°时。结构上另一侧的节点如11591号和11722号节点的变化,如图6(b)所示。其z轴向加速度受相干系数和相位角影响的变化规律与232号节点完全相反。另外，对于结构上不同位置受载荷相关影响产生的最大与最小加速度的差值也是不同的，如表3所示。

2.3.2 载荷相关性对应力的影响

对两轴向不同耦合工况下结构的von Mises 应力进行了计算分析，研究结果表明：结构上各点应力随两轴向载荷谱间相干系数和相位角的改变呈规律变化，典型节点von Mises 应力的变化规律如图7所示。其规律与加速度响应的变化规律相同，但是也存在一定差别：位于结构x和y轴向对称轴上的12605和12862号节点(见图1)，其von Mises应力随相干系数和相位角的改变而发生规律变化，进一步说明相比于结构的加速度响应，结构的应力响应的多轴效应更为明显。另外，不同节点在不同耦合工况下的应力增量也是不同的，说明载荷谱间的相干性对结构上的不同位置影响程度是不同的。

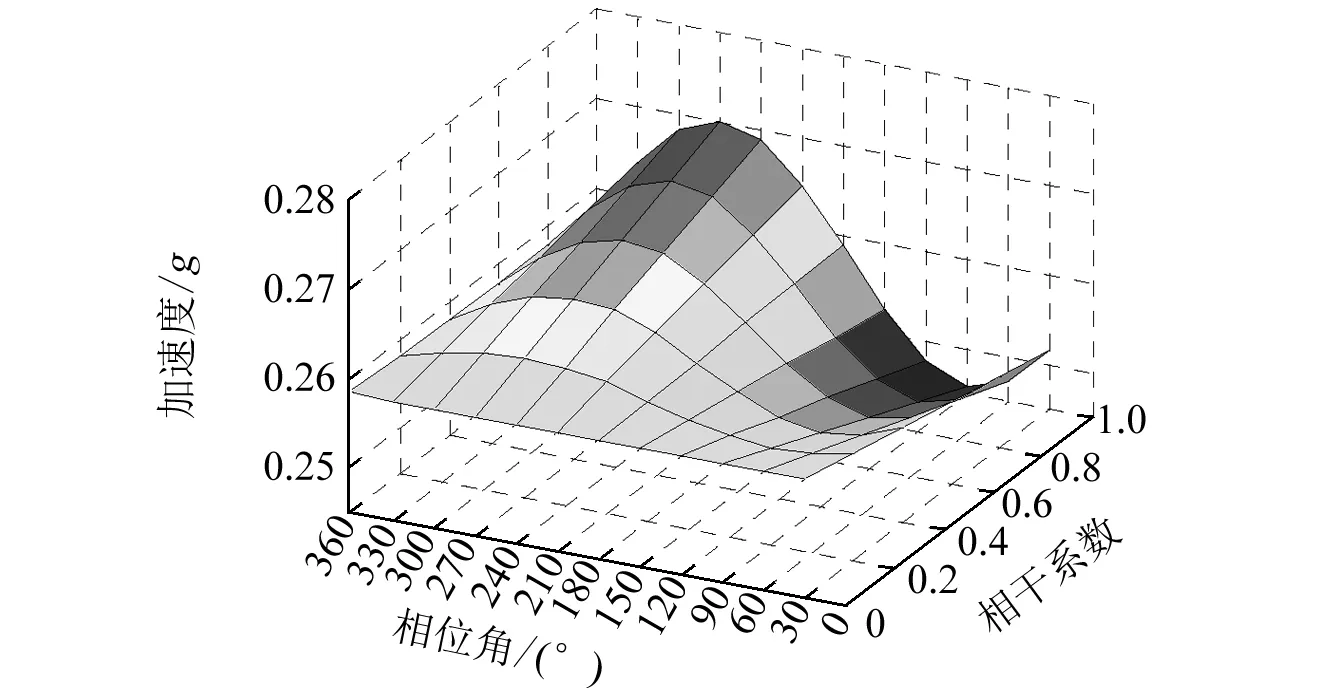
(b)11591号节点图6 不同耦合工况下z轴向加速度响应Fig.6 The RMS of z-axial acceleration of different coupled load cases

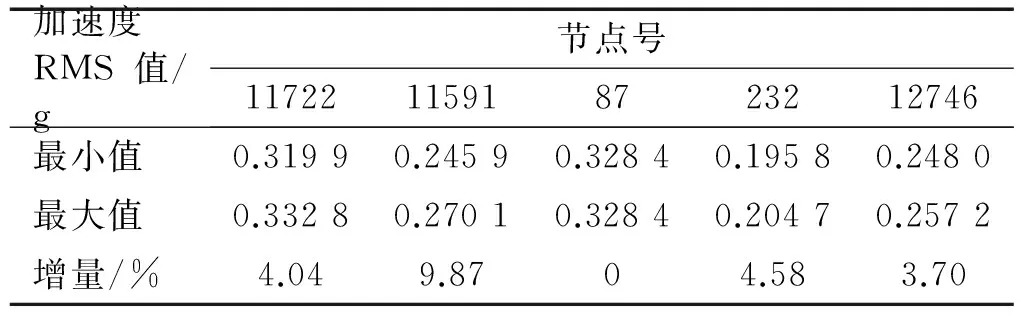
加速度RMS值/g节点号11722115918723212746最小值0.31990.24590.32840.19580.2480最大值0.33280.27010.32840.20470.2572增量/%4.049.8704.583.70

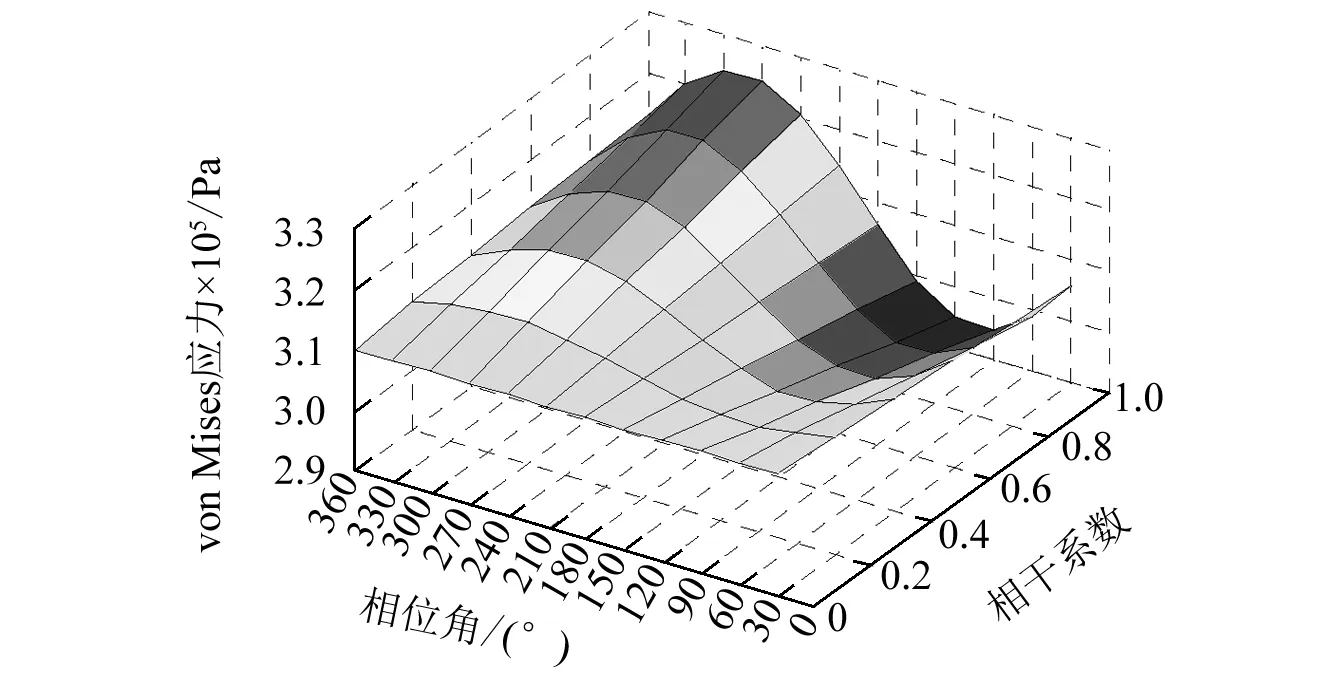
(a)7199号节点

(b)1006号点图7 不同耦合工况下von Mises应力变化图Fig.7 The RMS of von Mises stress of different coupled load cases

3 试验研究

3.1 试验试件与试验系统

试验件,如图8所示。其尺寸以及材料与仿真模型一致，试件由整块型材通过线切割加工而成。通过试验测得试件在安装完成后的前三阶固有频率分别为121.25 Hz，186.5 Hz和213.5 Hz，与仿真结果吻合较好。试验系统主要由多轴向振动控制系统，加速度测试系统和动态应变测试系统三部分组成。多轴向振动控制系统通过三个加速度计将台面三个轴向的加速度反馈给控制系统实现多轴向振动环境的控制；加速测试系统包括加速度计和动态信号分析仪，实现典型位置加速度的测量和记录；动态应变测试系统通过应变片和动态应变仪测量并记录结构典型位置处的应变响应。

图8 试验试件和试验现场Fig.8 The photo of the test specimen and test field

3.2 试验过程与结果分析

对试验件分别进行三轴向互不相关的同时振动试验，以及x，y和z轴向单轴向振动试验。三轴向与单轴向试验中各个轴向的加速度载荷谱功率谱密度均与动力学仿真相同。

3.2.1 加速度响应分析

通过加速度计和动态信号分析仪测量记录结构典型节点处的加速度响应，为了便于对比分析，测点位置与动力学仿真位置相同。通过对比三轴向振动与单轴向振动工况下x，y轴向的加速度响应(如图9为y轴向响应)，得到与仿真结果(见图2)相同的结论，即对于结构在某些轴向的加速度响应主要是由本方向振动激发的模态引起的。

对典型节点进行了三轴向同时振动与z轴向单轴振动工况的z轴向加速度测量分析结果,如图10所示。由图可见在三轴向同时振动工况下结构上各点的加速

(a)三轴向振动

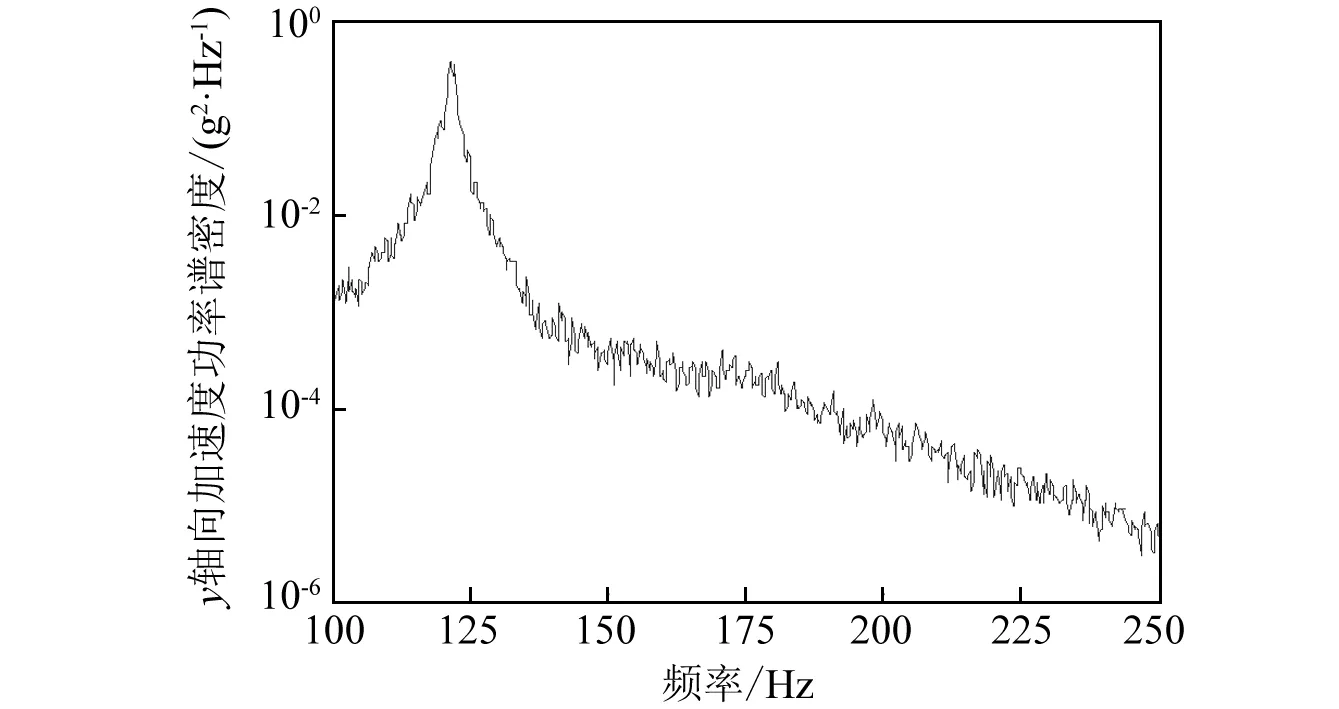
(b)y轴向振动图9 不同工况下y轴向加速度PSDFig.9 The y-axial acceleration PSD of different load cases

度功率谱密度图的第一个峰值比仿真结果大，可能的原因是在实际三轴向振动试验中y轴向的控制谱量级略大于参考谱的量级，导致结构的第一阶模态在振动中被放大。除此之外，三轴向振动与z轴向振动所测得的试验结果与仿真结果(见图3)基本一致。

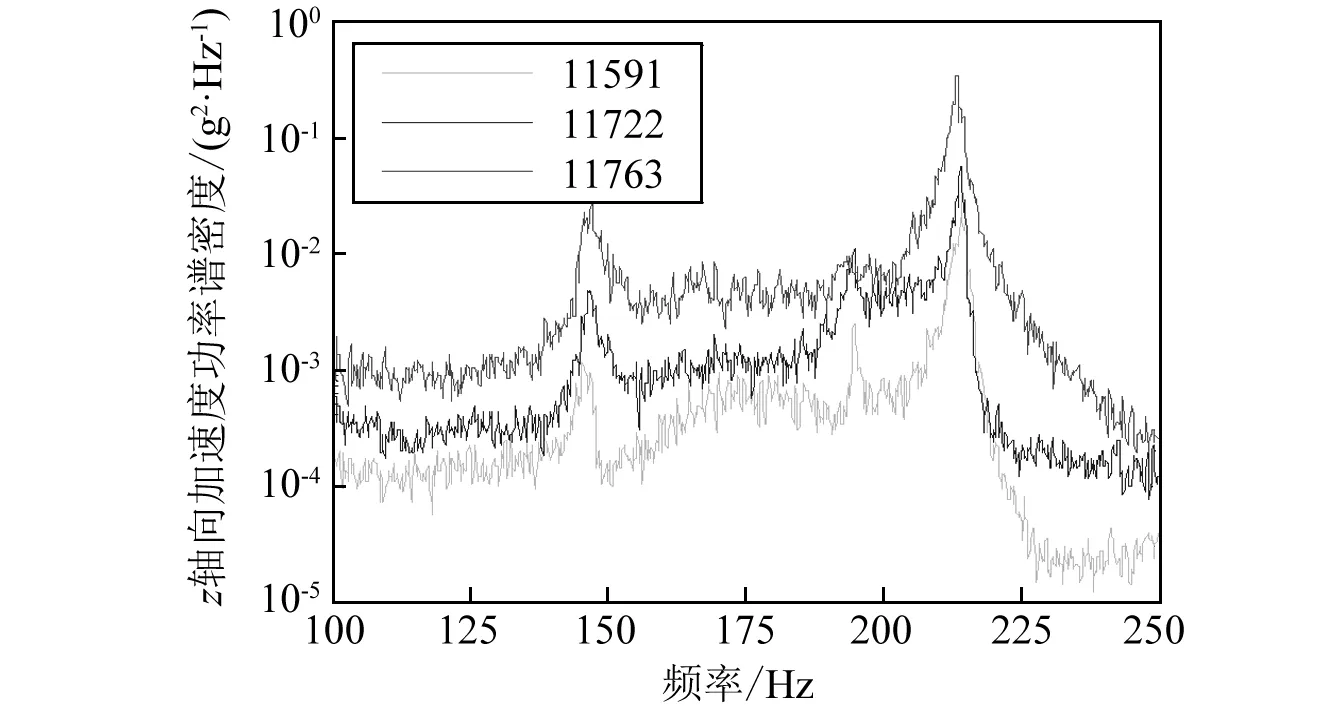
(a)三轴向振动

(b)z轴向振动图10 不同工况下z轴向加速度响应Fig.10 The z-axial acceleration PSD of different load cases

为了研究结构在三轴向同时振动与单轴向振动时加速度响应之间的关系，对结构分别进行了x和y轴向的单轴向振动试验，试验中对典型节点z轴加速度响应进行了测试，结果如图11所示。由图可见当结构受到x轴或y轴向激励时，z轴向加速响应中结构的第二阶模态和第一阶模态振型被激发，这与分析结论一致。与仿真结果不同的是图中出现了第三阶模态振动引起的峰值，其原因可能为三轴向振动台的并非完全解耦，通过三轴振动台进行单轴向振动试验时，结构实际所处的振动环境并非绝对的单轴向振动环境，从而导致结构的某些轴向的敏感模态振型在实际振动环境中能够被激发出来。

(a)x轴向振动

(b)y轴向振动图11 单轴向振动时在z轴向引起的加速度响应Fig.11 The z-axial acceleration PSD under uniaxial load cases

通过典型节点不同工况下加速度响应的时域信号，计算了各个节点在不同工况下z轴向加速度的均方根值，试验结果如表4所示。

由表中数据可知结构在各轴向载荷谱互不相干的三轴同时振动下的加速度度响应基本满足理论分析中式(14)所表示的关系。另外，通过数据看出，结构在三轴向单独振动时引起的加速度的叠加大于三轴向同时振动时的加速度值，其原因是在实际单轴向振动试验中，结构敏感模态(z轴向第三阶振型)也被激发出来(见图11)，因此导致了单轴向振动时结构在z轴向的响应大于理论计算的响应。

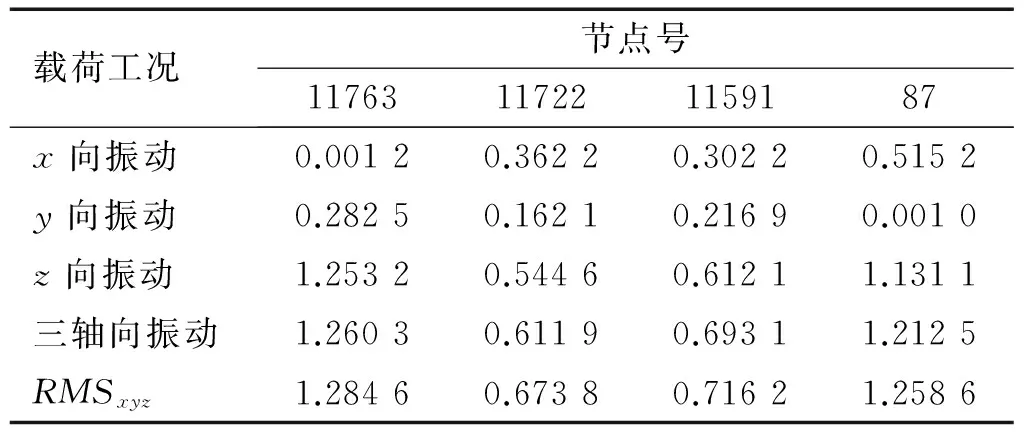
表4 不同工况下z轴向加速度RMS值

3.2.2 应力响应分析

von Mises应力是金属材料强度问题的考核的重要指标，但是von Mises应力为当量应力，在试验中无法全部测量结构各点的应力分量，因此通过试验无法得到结构上节点的von Mises应力值。为了验证多轴振动环境下的应力响应的模态参与情况，本部分在三轴向振动环境和单轴向振动环境下对典型节点(节点号：12605，12682，见图1)处的x和y轴向线应变，以及典型节点(节点号1006)的z轴向线应变进行了动态测试。将测得的应变信号转化为应力信号，根据式(15)通过MATLAB编制程序计算不同工况下各轴向正应力功率谱密度。

(15)

式中:N为采样点数;h为采样间隔;Xk为应力时域信号的离散傅里叶变换。

图12为三轴向振动工况下各节点三个方向应力分量的功率谱密度图，图中都出现了三个峰值，说明三轴向同时振动激发了结构在三个方向上的模态振型，在应力响应的计算中结构的前三阶模态振型都有贡献。这与动力学仿真结果(见图4)与分析结果一致。

(a)正应力σxx (b)正应力σyy (c)正应力σzz图12 三轴向激励下正应力功率谱密度Fig.12 The PSD of normal stress under 3-axial excitations

通过对单轴向振动试验数据分析可知，试验结果与仿真结果基本一致，同时证明了理论分析的结果：理论上在单轴向振动环境下，结构的应力响应只与该轴向振动引起的模态振型有关，与其它轴向振型无关。在试验结果中在第三阶模态振型的频率点上，应力的功率谱密度有小的峰值出现，其出现原因与图12结果分析相同。典型节点在y轴向振动环境下的三个方向正应力分量的功率谱密度,如图13所示。

(a)正应力σxx (b)正应力σyy (c)正应力σzz图13 y轴激励下正应力功率谱密度Fig.13 The PSD of normal stress under y-axial excitation

4 结 论

分析了结构在三轴向同时振动与单轴向振动环境下动力学响应之间的区别于联系，以及各轴向载荷相关性对结构动力学响应的影响；通过动力学仿真，对不同工况下结构的动力学响应进行了量化分析；通过不同工况下典型构件的动力学响应测试，对上述结论进行了试验验证。得到以下主要结论：

(1)结构在单轴向振动环境下，动力学响应仅由该振动方向所激发的模态振型计算得到的；多轴向振动环境下，会激发出结构的不同方向的多个模态振型。另外，通过研究发现在多轴振动环境下结构的应力响应比加速度响应具有更为明显的多轴效应。

(2)在不考虑各轴向载荷相关性的工况下，三轴向同时振动工况下结构上某点的动力学响应为该点在各个方向做单轴向振动时引起的动力学响应的叠加，因此，多轴向同时振动环境下结构的动力学响应明显高于单轴向振动环境下的动力学响应。并且由于叠加作用，结构上动力学响应的极值位置以及方向也与单轴向振动不同。

(3)在各轴向相关的载荷工况下，结构上各点的动力学响应随着载荷谱间相干系数和相位角的改变的呈规律变化：相位角相同的工况下，相干系数越大对动力学响应的影响越明显；相干系数相同的工况下，动力学响应随相位角的改变呈类似正弦规律变化，极值响应出现在相位角为90°或270°时，且变化规律受到节点位置的影响而不同。

[1] 夏益霖. 多轴振动环境试验的技术、设备和应用[J].导弹与航天载运技术，1996，6:52-59.

XIA Yilin. The technology equipment and application of multi-axis vibration environment testing [J]. Missiles and Space Vehicles,1996, 6:52-59.

[2] HABTOUR E, CONNON W S, POHLAND M F, et al. Review of response and damage of linear and nonlinear systems under multiaxial vibration [J]. Shock and Vibration, 2014,2014: 1-21.

[3] FREEMAN M T. 3-axial vibration test system simulates real word [J]. TEST Engineering and Management, 1990, 91: 10-14.

[4] WHITEMAN W E. Inadequacies in uniaxial stress screen vibration easting [J]. Journal of the IEST, 2001, 44 (4): 20-23 .

[5] WHITEMAN W E, BERMAN M S. Fatigue failure results for multi-axial versus uniaxial stress screen vibration testing [J]. Shock and Vibration, 2002, 9(6): 319-328.

[6] FRENCH R M , HANDY R, COOPER H L. Comparison of simultaneous and sequential single axis durability testing [J]. Experimental Techniques, 2006, 30(5):32-35.

[7] ERNST M, HABTOUR E, DASGUPTA A, et al. Comparison of electronic component durability under uniaxial and multiaxial random vibrations [J]. Journal of Electronic Packaging, 2015, 137 (1): 1-8.

[8] 贺光宗，陈怀海，贺旭东. 一种多轴向随机激励下结构疲劳寿命分析方法[J]. 振动与冲击, 2015, 34 (7):59-63.

HE Guangzong, CHEN Huaihai, HE Xudong. A vibration fatigue life prediction method of the structure under multi-axial random excitation [J]. Journal of Vibration and Shock, 2015, 34 (7):59-63.

[9] PAULUS M ,DOUGHTY K. Effect of resonant frequency shifting on time to failure of a cantilevered beam under vibration [J]. Journal of the IEST, 2010,53(1):59-68.

[10] 唐振杰，史展飞，胡海涛. 不同频率激励下 LY12 铝合金悬臂梁的疲劳特性[J]. 材料科学与工程学报, 2012, 30 (3): 384-388.

TANG Zhenjie, SHI Zhanfei, HU Haitao. Fatigue properties of LY12 cantilever beam under diffferent vibration frequencies [J].Journal of Materials Science& Engineering, 2012,30(3):384-388.

[11] FÜLLEKRUG U, SINAPIUS M. Simulation of multi-axis vibration in the qualification process of space structure [C]//2nd Int Symp Environmental Testing for Space Programmes. 1993, 143-151.

[12] FÜLLEKRUG U. Utilization of multi-axial shaking tables for the modal identification of structures [J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2001, 359 (1786): 1753-1770.

[13] 陈颖，朱长春，李春枝，等. 典型结构在单、多轴随机振动下的动力学特性对比研究[J]. 振动工程学报，2009，22(4)：386-390.

CHEN Ying,ZHU Changchun, LI Chunzhi, et al. Comparison of dynamic characteristics of a typical structure under single-axial and multi-axial random vibration loads[J]. Journal of Vibration Engineering, 2009, 22(4):386-390.

[14] WIJKER J J. Random vibrations in spacecraft structures design: theory and applications[M]. New York: Springer Science & Business Media, 2009.

Dynamic responses of structures under multiaxial and uniaxial random excitations

HE Guangzong1,2， CHEN Huaihai2， SUN Jianyong3

(1. School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China；2. Aerospace College, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China；3. China Aero-Polytechnology Establishment, Beijing 100028, China)

In order to evaluate the vibration failure behaviors of structures under multiaxial and uniaxial excitations, contrast theoretical analyses, finite element analyses and experiments on the dynamic responses of structures under multiaxial and uniaxial excitations were performed. The results show that the structural vibration modes in different directions can be excited simultaneously under multiaxial excitations. Under three simultaneous uncorrelated axial excitations, the responses of structures are the square root of the sum of the squares of each uniaxial excitations results. If the random excitations are correlated, there are significant effects of input correlation on the dynamic responses, and the effects are of regularity. In addition, the reasons for the phenomena mentioned above were also analyzed. The study provides references for the vibration failure behavior analysis of structures under multiaxial and uniaxial random excitations.

dynamic response ; multiaxial random excitation; vibration fatigue; modal shape

航空科学基金重点项目(20140241002)

2016-04-14 修改稿收到日期： 2016-06-07

贺光宗 男，博士，讲师，1980年生

O342；V416. 2

A

10.13465/j.cnki.jvs.2017.14.031