整星减冲击装置设计及试验研究

严鲁涛， 李 红， 丁 洋， 王有杰， 杨志鹏

(北京强度环境研究所，北京 100076)

整星减冲击装置设计及试验研究

严鲁涛， 李 红， 丁 洋， 王有杰， 杨志鹏

(北京强度环境研究所，北京 100076)

减冲击装置可以有效降低基础对有效载荷的冲击，在航天领域内的有效载荷及箭体分离过程中应用广泛。建立了减冲击装置数学模型，设计优化了结构尺寸，并制作了减冲击环样机；在响应板式爆炸冲击台上开展了冲击试验，并对冲击数据进行了冲击响应谱分析。结果表明，所设计的减冲击装置满足指标要求，而且大幅衰减了冲击幅值；此外，讨论了阻尼层对结构动力学特性及减冲击特性的影响；减冲击环结构适用于航空航天冲击环境，也适用于各类导弹仪器舱的整体冲击隔离，具有广阔的应用前景。

整星减冲击装置；模型；冲击试验；冲击响应谱

航天领域内，火工装置可实现星箭分离、卫星舱段分离、星上展开部件解锁、设备驱动等功能[1]。火工装置爆炸时在邻近结构上产生剧烈的局部机械瞬态响应，应变能的突然释放急剧增加了冲击环境的烈度。而后续冲击则是以应力波形式传播，对搭载的卫星和各类航天器造成高频冲击影响，特别是对电子产品、轻薄结构、脆性材料等的破坏作用更为明显[2]。

冲击过程中，减冲击装置将瞬态、强烈的冲击能量以弹性势能的形式储存，然后按本身的特性缓慢的将能量释放出来，从而减少激励从基础传递到设备或从设备传递到基础所引起的响应，以达到保护设备的目的[3]。一般多采用橡胶、泡沫铝、蜂窝等材料作为各类敏感仪器的减冲击措施，具有轻量化、高阻尼、寿命长等优势[4-6]。然而，上述材料特性受温度影响较严重，且具有明显的刚度非线性特征，对航天器姿控系统造成不可预知的影响，不利于标准化设计。

目前，在卫星载荷的边界设计集中在振动隔离措施，包括局部隔振及整星隔振，具体方式多采用弹性支撑加粘弹性阻尼结构[7]。然而，冲击隔离不同于振动隔离，振动隔离主要研究减少振动基础或激励向负载的传递，属于稳态过程。冲击隔离主要考虑减少负载的瞬时加速度值，同时防止过大的相对位移，属于瞬态过程。

对于爆炸环境的减冲击措施，仅有少量文献。CSA公司的Conor等[8-10]研制了多种类型的整星振动及冲击隔离装置，并完成了多项运载火箭的卫星发射任务。然而，国内关于航天领域的爆炸冲击隔离结构研究较少，且国外文献未涉及具体的设计过程及理论模型。

本文建立了应用于爆炸冲击环境中的减冲击环结构模型，围绕技术指标设计了减冲击环的具体尺寸，并研制样机。开展相关冲击试验，并研究切向阻尼层对减冲击效果的影响。

1 结构设计模型

减冲击环位于卫星和支架连接界面处，相当于串联增加了弹性环节，将对整体刚度有一定影响。而且，在爆炸冲击过程中实现星箭分离，应尽量降低支架与卫星的相对位移，以防对分离姿态造成影响。因此，减冲击环应具有较高刚度而不影响整体频率。其次，需要尽量降低冲击应力波至卫星的传递，而影响应力波传递的主要因素是界面的透射、反射以及传播路径距离(由两侧界面的阻抗性质决定)[11]；最后，处于有效载荷及运载成本，应尽量降低减冲击环的整体尺寸及质量。

结合相关文献，减冲击结构一般采用分层式结构，且连续圆环层和隔离块层交错布置，如图1所示。

图1 分层式减冲击结构Fig. 1 Multi-layered shock isolator

引入变量：hc为连续层高度；hd为隔离块层高度；N为连续层数；Nd为单层隔离块数；ρc为连续层密度；md为隔离块质量。同时环形内径r及外径R均为设计值。

将隔离块之间的连续层视为两端固支梁，则总体的刚度可以表示为

(1)

式中：K为整体刚度；E为连续层材料弹性模量。

应力波从底面传递至顶面的距离为

(2)

冲击环整体质量：

m=Nπρc(R2-r2)hc+(N-2)Ndmd

(3)

因为冲击环的整体高度影响到刚度及包括卫星在内的整体转动惯量，因此增加约束

Nhc+(N-2)hd≤H0

(4)

此外，当最大冲击载荷P施加时，应满足：

(5)

根据卫星及接口模型可以通过有限元或模态试验方法，得到整体的各阶频率及振型。将卫星及减冲击环整体视为单自由度系统，依据减冲击环对各阶频率的允许影响误差，并结合有效载荷的整体质量，可以得到减冲击环的最小允许刚度。根据整体质量及高度指标，并结合上述刚度允许值，结合式(1)～式(5)，可以得到减冲击环的结构尺寸范围。

在材料选择方面，为增加冲击应力波的衰减量，首先选择比刚度差别大的两种材料作为连续层及隔离块材料；其次，在连续层及隔离块连接处，使用上、下结合面分别连接的形式，避免应力波未经隔离块而直接通过连接螺栓传递至下一连续层。最后，在减冲击环的侧面设置阻尼层，一方面增加部分垂向刚度，一方面吸收应力波的能量。

在已有卫星及接口模型的前提下，设定技术指标为：有效载荷50kg；冲击载荷峰值衰减>10dB； 减冲击环质量<20kg； 减冲击环厚度<100mm；有效载荷垂向刚度>1.6×107N/m。

根据上述结构设计过程，首先分析刚度随连续层高度、单层隔离块数目及总层数情况，如图2所示。从图2可知，刚度随连续层高度及隔离块数目的增加而升高，但层数越多刚度越低。根据指标，结合质量、厚度等指标，选择总层数为5，连续层高度为9.5mm，隔离块数目为20。

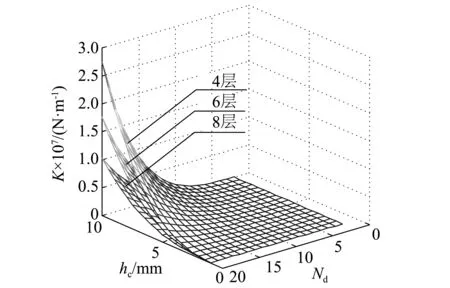
图2 刚度曲面Fig. 2 Effect of shock isolator parameters on vertical stiffness

设计并制作了减冲击环样机，具体形式如图3所示。详细参数如表1所示。连续层的材料为钢，隔离块选用比刚度较低的胶木材料，以增加应力波的传波界面，且胶木块与连续环的连接接口使用钢丝螺套结构。

图3 减冲击装置样机Fig. 3 Shock isolator

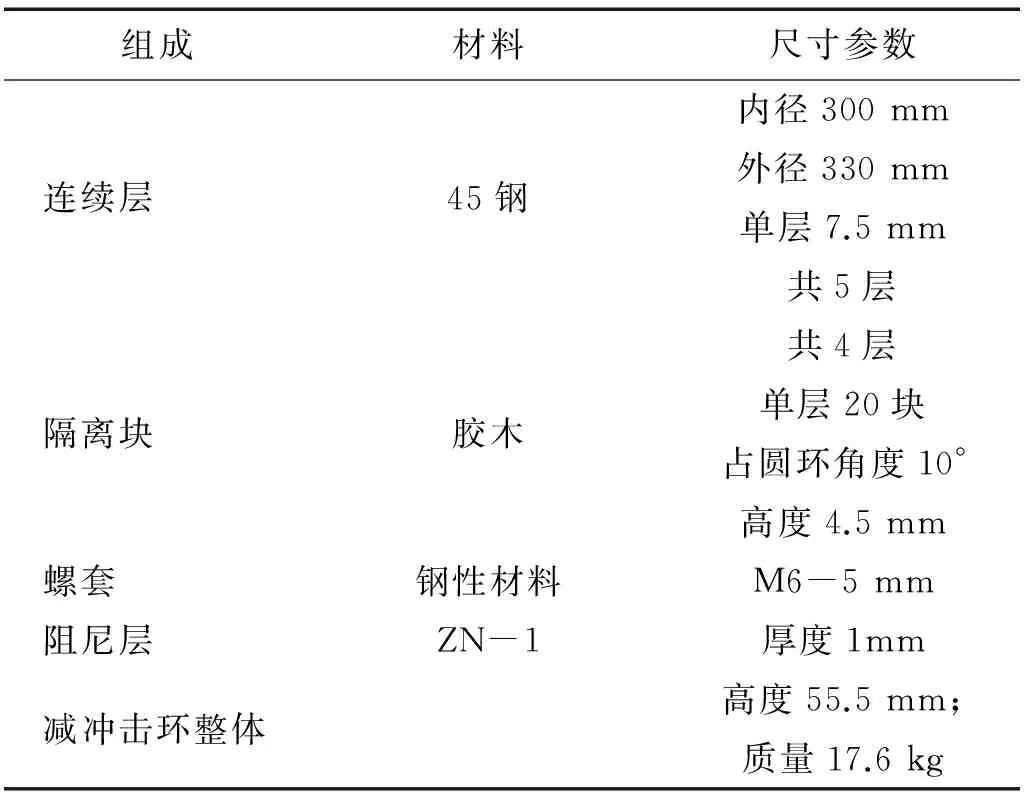
组成材料尺寸参数连续层45钢内径300mm外径330mm单层7.5mm共5层隔离块胶木共4层单层20块占圆环角度10°高度4.5mm螺套钢性材料M6-5mm阻尼层ZN-1厚度1mm减冲击环整体高度55.5mm;质量17.6kg

2 试验及结果分析

2.1 冲击衰减试验

模拟载荷与减冲击环构成模拟系统安装在响应板式爆炸冲击台(Mechanical Impulse Pyro Shock, MIPS)中，如图4所示。MIPS是以高压气为动力，驱动弹丸来打击响应板，使之产生类似于爆炸冲击的高频振荡环境。高速弹丸冲击在钢板上以模拟减冲击环的基础激励，通过采集减冲击环上下界面的加速度得到减冲击特性。

冲击响应谱采用1/12倍频程分析带宽，放大倍数取10(对应阻尼比为0.05)，频率范围100～10 000 Hz(冲击拐点频率为1 000 Hz)。

图4 冲击试验Fig.4 Impact test system set-up

2.2 结果及分析

通过数据采集，垂直方向的减冲击效果如图5所示。在经过迭代运算后，MIPS冲击台得到了要求的冲击输出波形，大量级冲击波形集中时间<15 ms。

可以明显看出，冲击加速度幅值经过减冲击环后大幅衰减。原始冲击信号加速度最大峰值为1 500g，经无切向阻尼层减冲击环后加速度响应峰值为48g，衰减了30 dB；经有切向阻尼层减冲击环减冲击后系统加速度响应峰值为107.5g，衰减了23 dB。

此外，由减冲击环及有效载荷构成的动力学系统，在经短时间的冲击载荷作用后，其冲击响应包含冲击过程中及冲击停止后的剩余响应。尤其对于无切向阻尼层的结构，系统阻尼较小，能量耗散较慢，所以在15 ms以后仍呈现较明显的动态响应。

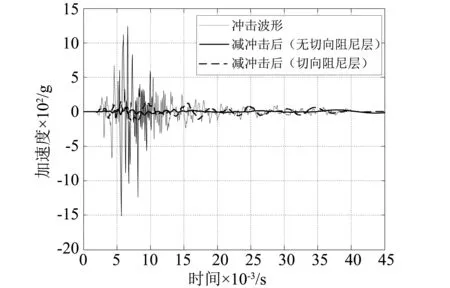
图5 垂向减冲击效果Fig.5 Shock attenuation in vertical direction

阻尼是动力学系统中的关键因素，在减冲击环结构中的阻尼设置在圆周外侧，起到增加冲击应力波能量耗散的作用。同时由于阻尼层材料为胶粘剂，在固化后在一定程度上提高了结构的垂向刚度。本文采用的阻尼材料为ZN-1型，以丁基橡胶和酚醛树脂为基础配制[12]。阻尼层布置于减冲击环外侧，厚度为1 mm(内径330 mm，外径331 mm)，高度为55.5 mm。

为分析阻尼对轴向刚度的影响，开展了振动试验。振动试验系统由试验件、振动台、振动控制仪、加速度传感器等组成。其中，试验件尺寸为370 mm×370 mm×50 mm，材料为45钢。振动台为本单位研制的5t电动振动台。试验进行时，将减冲击环通过转接工装固定在振动台台面上，使用振动控制仪生成随机振动，同时采集减冲击环上下的采集点加速度，并利用传递函数估计得到动态特性。根据试验数据，阻尼对轴向振动传递特性的影响，如图6所示。

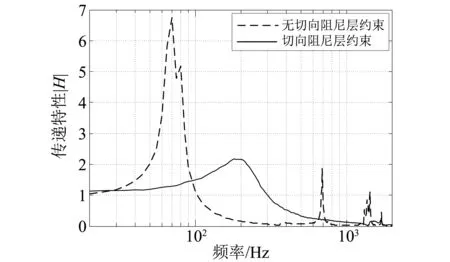
图6 阻尼对轴向传递特性的影响Fig.6 Effect of damping on response function

可以明显看出，阻尼层提高了轴向刚度，降低了传递曲线峰值。具体而言，无阻尼层减冲击环的轴向一阶谐振频率为70 Hz，放大倍数是Q=6.925。施加约束阻尼层后，轴向一阶谐振频率提高到175 Hz，放大倍数减小为Q=1.968。按照单自由度系统，由频率175 Hz及质量50 kg计算，垂向刚度约为6.0×107，满足刚度设计指标。

阻尼对减冲击效果的影响，如图7所示。阻尼层设置后，垂向刚度增加，幅值衰减程度略低于无阻尼结构。无阻尼情况下的加速度度峰值更低，但冲击影响时间更长。此外，冲击波在经过阻尼层的作用后，能量被较大程度耗散，冲击影响过程较短。

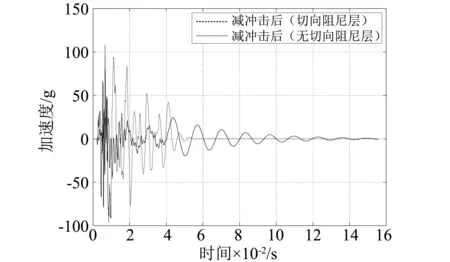
图7 阻尼对减冲击效果的影响Fig.7 Effect of damping on shock attenuation

冲击响应谱体现了整体结构的冲击参数(位移、速度、加速度等)最大值，由系统的固有频率、阻尼比以及冲击持续时间确定。

采用递归算法得到各冲击波形的冲击响应谱(加速度)，如图8所示。可以明显看出，经减冲击环后的冲击波形在300 Hz以后谱值衰减较为明显。冲击响应谱曲线的拐点频率由动力学传递特性决定，因此无阻尼情况下垂向刚度弱，拐点频率略低，但低频段的加速度响应略高于施加切向阻尼工况。施加切向阻尼后，拐点频率较高，低频段的响应有所抑制，但高频段的最大响应值较大。总体而言，减冲击环起到了减冲击效果，在具体载荷下可以优化结构参数并实现预期的减冲击效果。

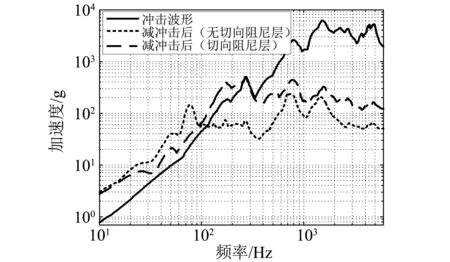
图8 冲击响应谱曲线Fig. 8 Shock response spectrum under different damping conditions

3 结 论

(1)围绕减冲击环的刚度、质量、应力波传递特性建立了结构设计模型，并研制了减冲击环样机；

(2)通过冲击试验，减冲击环可以有效降低冲击幅值。阻尼层布置于减冲击环外侧，由于固化胶剂的作用，在一定程度上提高了结构的轴向刚度。施加阻尼及无切向阻尼结构可分别衰减23 dB及30 dB，而且切向阻尼作用下可以缩减冲击波影响时间；

(3)通过冲击响应谱分析，减冲击环可以实现预期的减冲击作用。切向阻尼作用使曲线拐点后移，但高频段最大响应较大；无切向阻尼作用时，曲线拐点较低，低频段最大响应较大。

[1] HUGHES W O, MCNELIS A M. Pyroshock environments characterized for spacecraft missions[R]. NASA/TP—2005-0194723, 2005.

[2] 张建华. 航天产品的爆炸冲击环境技术综述[J]. 导弹与航天运载技术, 2005(3): 30-36. ZHANG Jianhua. Pyroshock environment of missiles and launch vehicles [J]. Missiles and Space Vehicles, 2005(3): 30-36.

[3] 周文亮,王强. 冲击隔离发展浅谈[J]. 噪声与振动控制, 2002(5): 22-25. ZHOU Wenliang,WANG Qiang. The development of shock isolation:an overview[J]. Noise and Vibration Control, 2002(5): 22-25.

[4] 肖锋, 谌勇, 章振华, 等. 夹层结构冲击动力学研究综述[J]. 振动与冲击, 2013, 32(18): 1-7. XIAO Feng, CHEN Yong, ZHANG Zhenhua, et al. A review of studying on impact dynamics of sandwich structures [J]. Journal of Vibration and Shock, 2013, 32(18): 1-7.

[5] 董彦鹏，吕振华. 基于蜂窝材料结构相似有限元模型的夹层结构抗爆炸冲击特性优化设计分析[J]. 工程力学, 2013, 30(7): 248-254. DONG Yanpeng , LÜ Zhenhua. Analysis and optimization of blast-resistant sandwich structure utilising structural similar FE model of honeycomb material[J]. Engineering Mechanics, 2013, 30(7): 248-254.

[6] 康建功, 石少卿. 沫铝衰减冲击波峰值压力的理论及数值分析[J]. 振动与冲击, 2010, 29 (5): 199-202. KANG Jiangong, SHI Shaoqing. Theoretical and numerical analysis for a cladding aluminum foam sandwich panel attenuating blasting wave pressure[J]. Journal of Vibration and Shock, 2010, 29 (5): 199-202.

[7] 张军, 谌勇, 骆剑,等. 整星隔振技术的研究现状和发展[J]. 航空学报, 2005, 26(2): 179-183. ZHANG Jun, CHEN Yong, LUO Jian, et al. Review of the whole-spacecraft isolation techniques[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(2): 179-183.

[8] CONOR D J, PAUL S W. Recent launches using the softride whole-spacecraft vibration isolation system[C]∥ AIAA Space 2001 Conference. Albuquerque, NM: AIAA 2001-4708, 2001.

[9] CONOR D J, PAUL S W. Protecting satellites from the dynamics of the launch environment[C]∥ AIAA Space 2003 Conference. Long Beach, CA: AIAA 2003-6266,2003.

[10] CONOR D, PAUL S W, SCOTT C P. Soft ride vibration and shock isolation systems that protect spacecraft from launch dynamic environments [C]∥Proceedings of the 38th Aerospace Mechanisms Symposium. Langley Research Center, 2006.

[11] 王礼立. 应力波基础[M]. 北京：国防工业出版社, 1985.

[12] ZN-1阻尼材料: GJB 979—1990[S].

Design and test for the shock isolation structure of a whole spacecraft

YAN Lutao, LI Hong, DING Yang, WANG Youjie, YANG Zhipeng

(Beijing Institute of Structure and Environment Engineering, Beijing 100076，China)

In spacecraft design, the isolator can be optimally located in the aft part of the satellite in order to attenuate the shock load from the launch vehicle. Based on a proposed analytical model, a shock isolator was designed, analyzed, and tested. Impact tests were conducted on a mechanical impulse pyro shock (MIPS) system. The experimental results show that the multi-layered shock isolator provides obvious reduction in shock load transmission from the support base to payload. Moreover, the effect of structure damping on stiffness, vibration transmission characteristics and shock attenuation was discussed. The shock isolator is suitable for use in spacecraft launch system, and the presented structure will develop to be a very effective means with great application prospect.

whole spacecraft shock isolator; analytical model; impact test; shock response spectrum

民用航天项目资助

2015-10-08 修改稿收到日期： 2016-04-03

严鲁涛 男，博士，高级工程师，1984年生

TB535；O324

A

10.13465/j.cnki.jvs.2017.14.022