机器人加工系统及其切削颤振问题研究进展

王战玺， 张晓宇， 李飞飞， 张顺琦， 秦现生

(西北工业大学 机电学院，西安 710072)

机器人加工系统及其切削颤振问题研究进展

王战玺， 张晓宇， 李飞飞， 张顺琦， 秦现生

(西北工业大学 机电学院，西安 710072)

采用工业机器人加工系统来实现航空、航天等领域的装配现场加工，是非常有效的技术途径。由于机器人加工系统的整体刚度过低，在实际加工过程中较易自激产生颤振现象，造成加工失效甚至断刀现象，是当前机器人加工系统应用研究需要解决的技术难题。通过对国内外先进机器人加工系统的研究综述，重点分析机器人加工系统的主要特点及切削颤振问题，以机器人加工系统的刚度模型和动力学模型为理论基础，以期进一步揭示机器人加工系统切削颤振机理。为提高机器人加工系统的加工精度和动静态性能而设计出更适合的切削颤振主动抑制技术，并对有待进一步解决的问题以及未来的研究方向进行了讨论与展望。

机器人加工系统；切削颤振；刚度模型；动力学模型；主动抑制

工业机器人已成为自动化生产线中必不可少的核心装备，广泛应用于执行焊接、搬运、装配、喷涂和抛光等工作。此外，以六自由度工业机器人为运动主体，末端夹持高速电主轴的机器人加工系统在材料移除领域得到了迅速的发展。此类机器人加工系统可执行铣削、镗削、钻削、磨削和切割等工作，相对于传统的数控机床，机器人加工系统拥有灵活性高、加工区域大和价格低的优势[1]。美国机器人工业协会(RIA)[2]关于机器人加工的一份白皮书中指出，近十年来机器人加工系统在航空制造业和汽车制造业等机械加工制造业中得到了非常广泛的应用。

对于航空、航天、造船、高铁、风电以及汽车等制造领域，在装配现场需开展大量的钻、磨、镗、铣等切削加工[3]。由于所要装配的零部件，如飞机的机翼、机身和发动机等尺寸大，结构、工装和工艺复杂，待加工型面可达性差，传统的多轴加工中心往往无法适应此类大型复杂结构件的制造和装配需求。为此，旨在替代人工作业的工业切削机器人，因效率高、空间可达性好、精度稳定，以及可便捷移动和快速重构能适应大型复杂的装配作业，已受到波音、空客及一些研究机构的关注。

工业机器人属于开链式多杆串联结构，其系统刚度较低。当机器人用于航空、航天等领域的装配现场，进行钛合金、镍基合金或复合材料等切削加工时，因这些难加工材料产生的切削力及扰动大，受到激励，机器人加工系统极易产生切削颤振，从而导致加工精度下降，甚至造成产品报废、机器人损坏的严重后果。据报道[4]，ABB公司在硬质铝合金铣削试验中已经发现，当机器人处于某一姿态，一旦纵向切深达到2 mm，就会发生较大振幅的铣削颤振，并造成工件表面严重损坏。若要将工业机器人用于装配加工，它的切削颤振问题必须予以解决。本文基于此，通过对国内外先进机器人加工系统的研究综述，重点分析机器人加工系统的主要特点及切削颤振问题，以期进一步明确机器人加工系统切削颤振机理，为提高机器人加工系统的加工精度和动静态性能而设计出更适合的切削颤振抑制技术，并对有待进一步解决的问题以及未来的研究方向进行了讨论与展望。

1 工业机器人加工技术与应用

工业机器人作为面向工业领域的多自由度机械手，被广泛用于汽车、电子、冶金、食品、航空航天等行业的自动化生产线，替代人工完成上下料、搬运、喷涂、焊接和清洗等作业。据统计[5]，2014年全世界范围内安装了近23万台工业机器人，其中在中国就57 096台，同比增长了近59%，约占全球工业机器人市场的1/4，其中应用到机械加工领域的工业机器人约占7%[6]，而且正在逐年增加。机器人加工系统一般由工业机器人通过快换法兰连接末端执行器的形式构成，末端执行器则根据功能的不同，集成了诸如高速电主轴、压力脚、传感测量单元(如法向调平单元、基准找正单元、加工测量单元)及其他附件组成部分(见图1)。在大型复杂零部件装配加工中，机器人加工系统拥有比多轴加工中心更好的空间可达性和更小的安装空间要求，以KUKA KR-300机器人为例，其地面安装空间区域半径仅为500 mm，工作空间，如图2阴影部分所示。故机器人加工系统能够灵活安装在装配现场执行自动化加工任务，并且能够快速更换末端执行器以执行各种加工任务。近年来，伴随着工业机器人在精度和离线编程技术方面的不断提升，工业机器人开始用于大型复杂产品的制造和装配，进行钻、镗、铣、磨等切削加工甚至于铆接的装配作业。

在制孔机器人方面，美国GEMCOR、EI(ElectroimPact)、意大利柯玛(COMAU)、德国宝捷(BROETJE-Automation)等公司从21世纪初就致力于制孔机器人的设计和研发，所开发的制孔机器人系统已在飞机制造企业得到了广泛引用，如F-16、F-22、F-2和T-50等飞机的垂尾壁板，C-130飞机的梁腹板，波音F/A-18E/F超级大黄蜂后沿襟翼，F-35飞机机翼上壁板，波音B-747、C-17等飞机的机舱地板，A380机翼壁板等均采用了机器人自动制孔技术[7-8]。

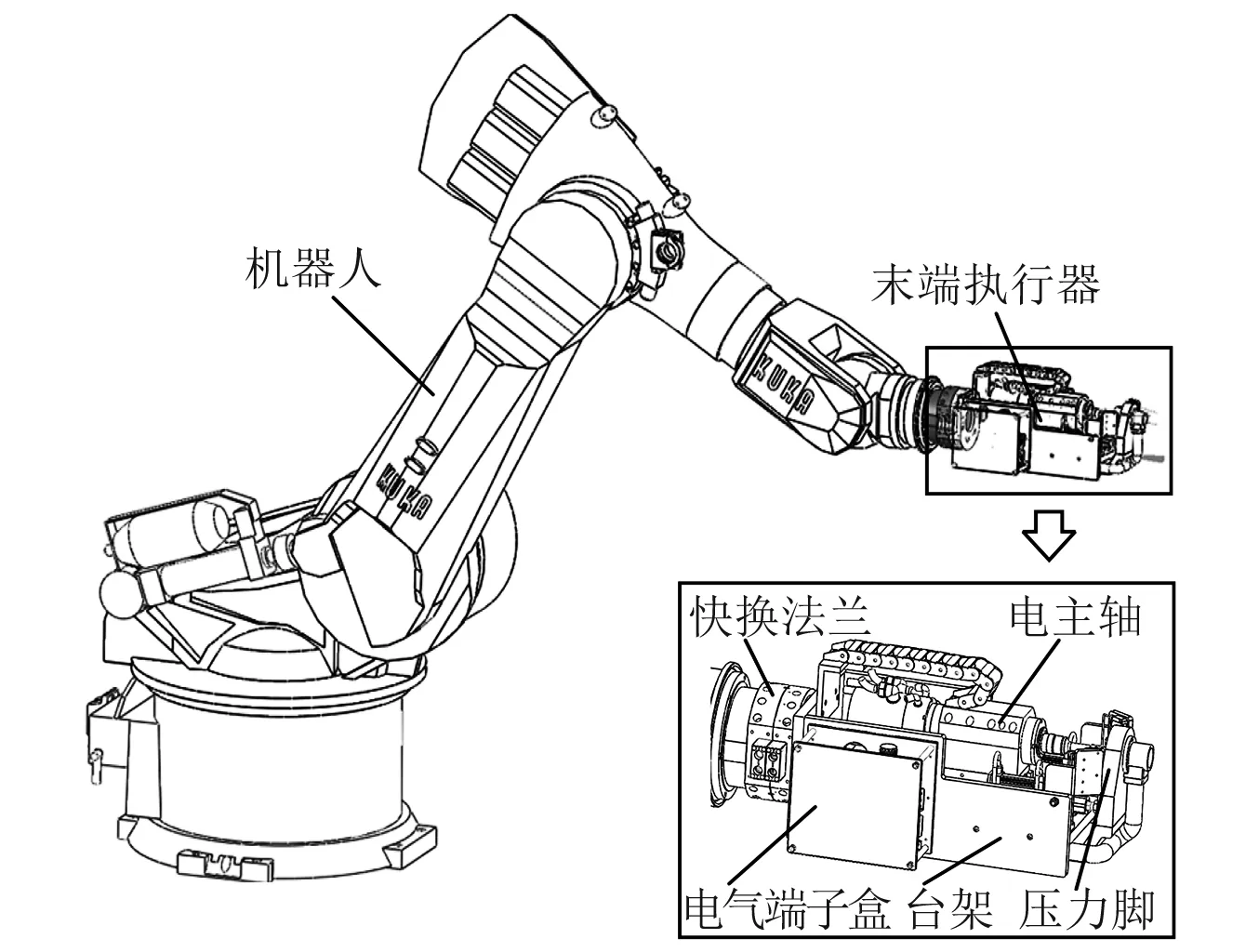
图1 机器人加工系统基本构成示意图Fig.1 Basic composition of robot machining system

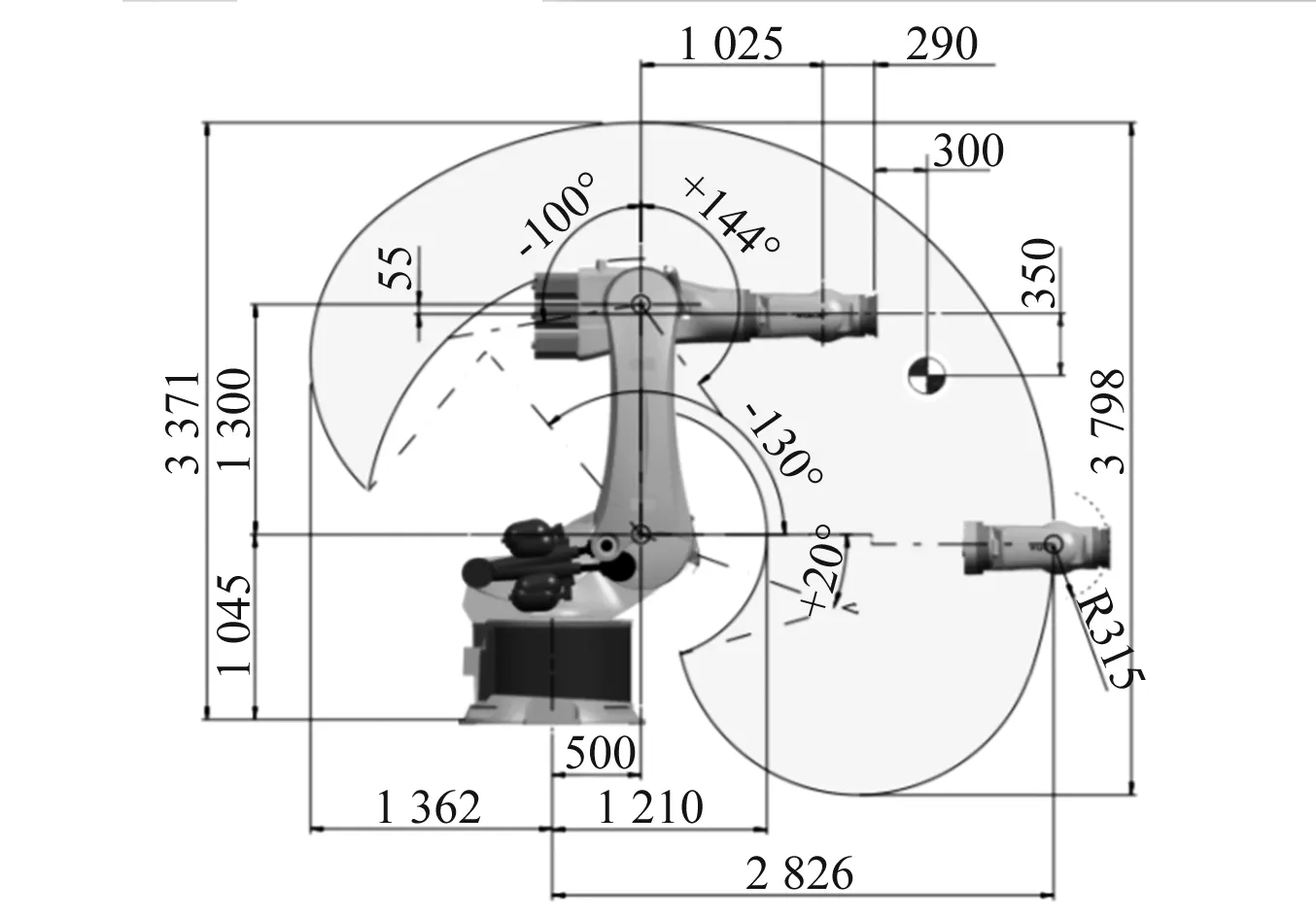
图2 机器人工作空间示意图(mm)Fig.2 The working space of robot(mm)

根据飞机自动化装配的技术需求，国内许多科研机构也先后联合主要飞机制造单位设计和研发了制孔机器人系统，并对涉及的关键技术问题展开了研究。曲巍威等[9]对机器人自动制孔系统中位姿补偿技术进行了研究，构建一种基于激光跟踪仪闭环反馈的机器人辅助飞机装配制孔系统，可以有效抑制多种残留误差，提高了制孔精度。Bi等[10]研制了制孔机器人系统，其采用工业相机建立工件与机器人坐标系之间关系，压力脚压紧采用压力反馈控制，可用于飞机钛合金和铝合金部件的自动制孔，同时针对机器人制孔垂直度问题，提出了一种曲面发现测量的新方法，利用定角度的二元角度调节法调节钻头的角度使其与钻孔点的法线重合，并经过制孔机器人平台的制孔实验验证了这种调节方法的高精度和高效性[11]。Zhao等[12]设计了一种飞机制孔六足机器人，采用行走-定位一体化的设计方案和力/位置混合控制策略，通过行走实验和工作平台位姿调整实验，验证了机器人行走和定位的性能指标。此外国内西北工业大学[13]、南京航空航天大学[14]、北京航空制造工程研究所等国内的研究院所也相继对制孔机器人系统展开了研究。

机器人铣削系统方面，EI公司[15]也为B-737的内襟翼装配研发了钻/铣一体的机器人加工系统；德国弗劳恩霍夫协会生产设备和结构技术研究所[16]研制了机器人铣削系统，开发了机器人的实时位置补偿算法，根据当前位置误差实时调节机器人运动速度，解决了因机器人关节摩擦力的非线性所造成的运动方向改变时误差增大的问题。Kihlman等[17-18]研制了面向钛合金和复合材料等难加工材料的机器人螺旋铣系统。谢祥南等[19]研制了机器人螺旋铣系统，针对加工过程中存在因偏心产生的非线性干扰，提出了基于自适应鲁棒控制理论的闭环伺服控制方法。单以才等[20]通过对机器人化螺旋铣过程的矢量分析，建立了两种典型加工方式的运动矢量方程，有效简化了机器人化螺旋铣系统的运动规划过程。

其他切削加工领域的工业机器人应用也在逐步增加，Rafieian等[21]针对一套机器人磨削系统，研究了切削深度、切削速度等一系列工艺参数对系统稳定性的影响，提出周期性切削力是引起机器人磨削加工系统的主要原因，并绘制出稳定域的叶瓣图。Wang等[22]研制了机器人砂带磨削抛光系统，并基于经典截面轮廓法，利用优化曲线的方法，提出变曲率曲面上磨削轨迹的优化算法，并在机器人带磨系统中进行了验证。张绍全[23- 24]研制了用于飞机主起落架交点孔精镗的机器人镗孔系统，并基于刚度最优原则，采用遗传算法对机器人制孔姿态进行了优化，增强了机器人制孔系统的定位精度和稳定切削能力。

工业机器人加工系统因其通用性强、工作效率高、稳定可靠、自动化水平高的特点，正逐步成为航空航天大型零部件装配加工领域的发展趋势。但由于其结构属于开链式多杆串联结构，使得它的系统刚度和抗大载荷扰动性能成为其薄弱环节，而由此引发的切削颤振严重影响了加工质量。Pan等在与ABB公司合作研发铣削机器人加工系统中发现，在对材料为硬质铝合金的铸造毛坯件进行铣削加工中，在机器人某一加工姿态发生了铣削颤振现象，颤振对工件表面造成了严重破坏，如图3所示。本文作者的研究团队在研发应用于某型号飞机机翼装配的机器人自动制孔系统时，在某一机器人位姿下对铝合金进行制孔加工时，同样遇到了切削加工中的颤振问题，在工件表面留下明显振动痕迹，造成了加工失效，如图4所示。

综上，机器人加工系统虽然无法完全替代传统数控机床加工，但在一些大型零部件、复杂型面、装配现场作业等加工场合具备鲜明的优势和特点。目前机器人加工系统的静态精度和动态稳定性是需要迫切解决的应用问题，其静态精度可以借助外部测量工具或者内部伺服机构进行补偿，如南京航空航天大学为提高机器人的定位精度，研究了空间网格化的机器人变参数精度补偿技术，利用激光跟踪仪在KUKA工业机器人上进行运动学标定验证补偿效果；而EI公司则舍弃KUKA专用的机器人控制系统，采用西门子840Dsl数控系统控制机器人，而且给机器人关节增加了二次反馈机制，使得机器人定位精度达到±0.25 mm[25]。机器人加工系统的动态稳定性主要由切削颤振问题引起，由于机器人特殊的开链式多杆串联关节结构特点，以及其加工过程中位姿的时变性，导致其切削颤振机理与机床切削颤振机理有本质上的区别，目前主要依靠工艺试验，借助人工经验试凑相对稳定的加工工艺参数，缺乏系统性的理论知识和解决办法。因此为提高机器人加工系统的加工质量和加工稳定性，必须研究和解决其切削加工过程中的颤振问题。

图4 制孔机器人加工过程的颤振现象Fig.4 Chatter phenomenon in machining process of robot drilling system

2 机器人加工系统的颤振机理研究

颤振是切削加工系统中发生的刀具和工件之间的相互振动，一直受到机械制造领域的关注。机器人加工系统的颤振是一种复杂的弹性动力学现象，主要由机器人加工系统整体结构从切削过程中周期性切削力中吸收能量而自激产生。机器人加工系统一般采取“工业机器人+末端执行器”的系统组成形式，根据不同的切削功能需求，其末端执行器形状和结构各异。研究机器人加工系统的颤振机理问题，需要从集成末端执行器的机器人加工系统刚度模型、动力学模型、颤振产生机制等方面入手进行综合分析，以揭示机器人加工颤振的产生机理。

2.1 机器人刚度模型

刚度是满足机器人加工精度和性能需求的重要指标，机器人加工系统的机械臂为多连杆串联的机械结构形式，其结构特点导致了机器人的整体刚度过低，例如传统数控机床的刚度往往是机器人整体刚度的数百倍，这也是机器人加工颤振产生的主要因素。

机器人制造商一般不提供工业机器人各个关节以及系统的刚度信息，针对机器人静力学刚度模型和计算方法，国内外许多学者和学术机构做了大量的研究工作。Pashkevich等[26]提出了一种具有被动连接的非线性刚度模型，针对平面三连杆机器人在三种不同姿态下的刚度性能和稳定性进行了研究，并提出了一种增强机器人刚性的方法；Alici等[27]以Motoman SK120机器人为研究对象，建立了机器人的运动学模型及雅克比矩阵，然后对机械臂的运动学性能进行分析，并根据传统刚度映射模型，设计了一种基于力/力矩传感器和激光跟踪仪的机器人关节刚度测量方法，实验设施如图5所示。最后对机器人末端笛卡尔刚度矩阵特性进行了分析。Zhang等[28]提出了使用Monte-Carlo方法模拟了D-H参数的不确定性特点，通过API激光跟踪仪测量和实验辨识的方法测得了KUKA-KR16机器人的刚度值，最后基于增强刚度模型得到了机器人笛卡尔刚度矩阵，并在笛卡尔空间内进行了末端位置补偿。

图5 机器人刚度辨识实验Fig.5 Robot stiffness identification test

机器人加工系统在切削加工过程中，整个系统机构一般处于某一固定姿态，系统所受的外载荷为加工 过程产生的周期性切削力。另外在某些切削加工过程中，为了加工稳定性，一般采用压力脚的方式在加工系统和被加工工件之间施加压紧力，使机器人加工系统和工件形成闭链机构，这种状态下的刚度分析和辨识研究需要考虑外部切削力载荷和压紧力共同作用的受力特点。Dumas等[29]以KUKA KR240-2型机器人为例，建立了在末端执行器受力和扭矩作用下的运动学模型，并分析了机器人的可达性和工作空间，忽略补偿刚度矩阵的作用，在关节刚性的假定下，建立了机器人静刚度模型，提出了一种高效、强鲁棒性的用于6R机器人关节刚度辨识的方法，可以用来确定任何六自由度串联机器人的关节刚度值，并通过实验分析了计算误差来源及其大小。朱健[30]采用微分变换法求出6自由度工业机器人的雅克比矩阵，通过测量在机器人末端所施加载荷与机器人末端位移辨识出机器人的刚度矩阵和关节刚度值；曲巍崴等从机器人姿态与刚度关系入手，基于传统刚度映射模型，对机器人刚度性能优化进行了研究，结果表明刚度优化可以提高镗削机器人的加工精度和性能。

机器人的刚度特性是加工颤振产生的主要因素之一，现有文献对机器人的刚度辨识主要集中在静力学刚度模型计算上。而在机器人加工系统进行切削工作中，针对工业机器人变结构和变刚度的特点，主要研究内容应关注在切削力和压紧力共同作用下的系统刚度模型，研究切削颤振现象与机器人刚度性能之间的关系，以期揭示和阐述机器人加工系统切削颤振的作用机理，并通过对机器人位姿、刚度性能以及加工参数的优化，达到抑制切削颤振的目的。

2.2 机器人加工系统动力学模型

工业机器人本身是多刚体/弹性体、多关节的变结构系统，在不同的机器人位姿下，其动力学特性也不同，而机器人加工系统的动力学模型是研究机器人加工系统颤振问题的理论基础。目前许多研究机构主要采用Newton-Euler和Lagrange方法来研究机器人多刚体系统的动力学特性，动力学建模常用弹簧和阻尼单元来对机器人关节结构进行抽象和简化，这种简化方式的误差要高于实际由杆件和梁构成机器人模型误差，相比之下参数辨识的方法更适合应用在工程实际的机器人系统以获得动力学参数。

机器人加工系统的动力学建模中，包含冗余第七轴(末端执行器)的各个关节的质量、刚度、阻尼等动力学参数辨识是建模过程的技术难点，另外机器人动力学方程具有非线性和强耦合性的特点，其求解计算过程也需要重点研究。当前动力学辨识的计算方法主要包括最小二乘法、频响函数实验法、谐波法和模态实验法等。Lopes[31]利用广义冲量的定义建立了具有移动平台的六自由度机械手的动力学模型，分别对机械手平台在静止和移动状态进行了动力学描述；Mohan等[32]根据理论推导和实验分析，同时考虑关节阻尼和柔性连接结构阻尼特性，建立了改进的具有刚性和柔性连接的机器人系统动力学优化模型。Qin等[33]提出一个串行机器人动力学参数系统连续的识别方法，采用全加速度计惯性测量单元测量摩擦参数化的关节位置和速度参数，通过计算得到连续的过程动态参数识别，并通过实验验证了识别方法的精度。静大海等[34]提出时变系统谐波频率与振型的在线识别算法，并利用波传播方法计算出3自由度机器人关节处的力与位移矢量，再由机器人关节面位移连续与力平衡条件求得机器人关节处的动刚，进而求得机器人关节面处的刚度与阻尼，试验表明此方法具有良好的跟踪能力与较高的计算精度。

在对外载荷为周期性切削力和工件压紧力的机器人加工过程的动力学建模中，其动力学参数的辨识要更为复杂。Abele等[35]建立了机器人加工过程中的结构模型，并对系统的刚度和其他动力学参数进行了分析和识别，提出了一种基于极性刚度和雅可比矩阵的笛卡尔刚度计算方法。方强等[36]对包含气动压力脚的机器人镗孔加工系统进行动力学建模，如图6所示。并对施加压紧力前后的系统稳定性进行分析，得出压力脚装置对机器人镗孔加工系统稳定性叶瓣图的影响。最后通过实际镗孔加工实验验证了机器人镗孔系统在不同压力脚压力下的加工稳定性，表明合理的压力脚压力可提高稳定切深，拓展加工稳定区域，有效避免加工颤振。

图6 机器人镗孔加工系统动力学模型Fig.6 Dynamic model of robot boring system

机器人加工系统的动力学特性存在参数耦合和随位姿变化的显著特点，对于不同切削类型的加工系统，其动力学模型还需考虑不同类型的切削动力学模型，目前这方面的研究还相对较少，缺乏相应的机器人切削系统动力学建模理论。根据上述已有参考文献，机器人加工系统动力学建模的研究主要应解决合理建模和动力学参数辨识等两个关键技术问题，其中系统的刚度和阻尼项则是对机器人加工颤振稳定性影响较大的关键因素，在建模和参数辨识的过程中需要重点保证其精度，只有建立合理准确的机器人加工系统动力学模型，才能研究和揭示机器人加工系统的稳定性规律和切削颤振机理。

2.3 机器人加工系统切削颤振机理

传统机床中的切削颤振研究已经历了数十年的理论探索和加工试验，积累了许多颤振稳定性分析方法和控制方法。但机器人加工系统开链式多杆串联结构在大切削力扰动激励下产生的颤振无法直接用传统铣床中的颤振机理解释。

目前国内外对于机器人加工过程中的颤振现象的研究仍处于起步阶段，Özer等[37]研究了一个二连杆机械臂模型的钻削加工颤振现象，研究结果表明可以利用主轴转速和节点刚度的变化来被动控制颤振现象的产生，同时绘制了不同节点刚度下的颤振稳定性叶瓣图。Mejri等[38]采用实验模态分析法进行了机器人铣削系统的稳定性分析，使用两自由度频域法绘制了机器人铣削的稳定性叶瓣图，通过仿真模拟和实验论证了刀具进给方向和机器人腕部轴线方向的关系直接影响机器人铣削加工的稳定性，另外切削深度、刀具转速和机器人位姿也都会影响系统的加工稳定性。

机器人切削颤振机理研究方面已发表的文献比较少见，目前仍在探索研究阶段，部分学者认为机器人切削加工系统的变结构、刚度低、多动力学参数耦合的特点导致其颤振机理有别于传统机床。其中Pan等研究了一个用来加工铸造毛坯件的铣削机器人系统的切削颤振机理，建立了切削力理论模型和结构模型，结果指出关节式机械加工机器人的颤振可能属于耦合模态，不同于一般切削机床的再生颤振机理；Pan等[39]建立了切削力模型和机器人颤振机理系统分析的结构模型，模型分析表明铣削机器人的结构刚度比数控铣床低两个数量级，并指出机器人切削颤振的产生原因是工业机器人固有的低刚度特性引起的，与传统数控机床的再生颤振不同；而Hazel等[40]运用高速相机发现机器人磨削加工系统中刀具和工件之间存在反复冲击的现象，经过对磨削机器人的加工颤振问题研究，指出了再生颤振机理可能是磨削机器人加工颤振的产生原因，并通过仿真计算给出了机器人磨削技工的稳定区域。Guo等[41]研究了机器人镗削过程中加工颤振机理，认为与机床镗削再生颤振不同的是发生颤振的是整个机器人镗削系统，而非镗杆本身，并通过压力脚增加与被加工工件之间的压紧力进行稳定性优化，结果表明在发生再生颤振之前，机器人可能已经发生模态耦合颤振。

通过目前的研究来看，机器人加工系统的切削颤振机理尚不明确，不同类型的机器人加工系统其颤振类型也可能存在差别，模态耦合颤振和再生型颤振的理论观点尚需要在机器人加工系统切削颤振中得到证实。另外机器人加工系统切削颤振的理论模型仍有待完善，需要在建立机器人加工系统的动力学模型的基础上进行多维振动模态分析，采用时域方法和频域方法求解颤振稳定域，揭示在不同加工工艺参数和机器人位姿下，系统质量矩阵、刚度矩阵和阻尼矩阵等动力学参数对切削颤振的作用机制，探索切削颤振的产生机理。

3 机器人加工系统切削颤振的主动控制

从机器人切削颤振机理的研究出发对其进行主动抑制，是提高机器人加工系统切削稳定性和精度的重要技术解决思路之一。仿生智能结构在振动主动控制领域具有独特的优势，它可以感知外界或内部状态变化，采取相应的优化控制来改变自身的形状、刚度和阻尼，从而改变主体结构的机械性能对振动实现主动控制，并且具有工作频带高、响应速度快、滞后小、体积小和不受连接方式限制等控制优点。特别是近年来，高性能智能材料的出现推动了智能结构振动控制技术的发展，为机器人加工系统切削颤振的主动抑制提供了有效的技术途径。

3.1 智能结构振动主动控制

振动主动控制就是根据检测和预测到的振动信号，通过特定控制策略实时计算所需要的最优控制力，由控制中心发送控制信号给相应的驱动装置，利用结构内置的驱动器借助外部能量输入对结构施加控制力，实现减振和消振的目的。

目前在航空航天、数控机床、机器人等领域，智能结构作为振动主动控制器已经被广泛研究。如Bhungalia等[42]设计了二次线性最优控制方法二次调节器，在二维有限元数学模型的压电智能结构振动主动控制中进行仿真验证。Narayanana等[43]比较了常增益速度反馈、李亚谱诺夫反馈、线性二次调节器方法用于控制智能结构的振动效果。Han等[44]基于经典的线性二次型高斯(LQG)控制算法，利用压电陶瓷致动器和压电薄膜传感器，对悬臂板的弯曲和扭转模态振动控制进行了仿真，结果表明LQG控制具有较好的鲁棒性。Prakah-Asante等[45]提出了将包括线性/非线性比例反馈控制、线性二次型高斯控制和自适应前馈控制相结合的多渠道控制方法，并将其用于粘贴有压电传感器和致动器的经典梁结构的振动控制。Sebastijanovic等[46]对压电智能结构在超音速飞行下壁板颤振的主动抑制作用进行了研究；Zhang等[47]对薄壁压电智能结构的振动主动抑制效果进行了研究；王民等[48]对电流变材料在切削颤振在线控制中的应用进行了研究，提出切削颤振的变刚度控制方法，并设计仿真实验验证了该方法的有效性。Silva等[49]利用压电材料被动提高车削/镗削过程的颤振临界值，增加了切削过程的稳定域，并进行了数值模拟和实验验证。数据显示通过比较频响函数，使用不同的控制参数激活压电驱动器，可以有效增加系统的阻尼加速能量耗散，使切削颤振得到主动抑制。

智能结构集传感和驱动于一体，既可以检测和预测结构的振动信号，亦可利用结构内置的驱动器对结构施加控制力，可以方便地布置在主体结构上任意位置，不受连接方式的限制，工作频带比系统结构频率高，响应速度快、滞后小，甚至可以直接与本体结构合为一体。另外机器人加工系统的整体刚度远低于数控机床，因此采用智能结构的驱动特点更容易改变机器人加工系统整体机械性能，如刚度特性、阻尼特性等，再结合合适的控制理论可以实现机器人加工系统切削颤振的主动抑制。

3.2 机器人振动控制

机器人加工系统切削颤振的主动抑制还可以参考机器人的振动控制问题研究。当前对机器人的振动控制主要有两种方法，一是采用创新的机械结构和实现模式，如Davis等[50]通过使用一个滑动质量可控的杆件，实现了柔性机器人的轨迹控制，并增加了整体结构的刚度，具有一定的抗振性能；Tso等[51]在机器人手臂中添加了‘Lyapunov-type’控制器，通过激光检测系统实现了柔性机器人的振动控制，提高了机器人末端执行器运动轨迹的精度；Shigang[52]则通过规划机器人的初始位形和关节运动，选择振动较弱的优化配置，从而达到抑制振动的目的；这种控制方式属于被动控制方式，它的控制缺乏灵活性，没有对突发的环境变化的应变能力，不能主动适应外界环境和激励的变化，且很难做到精确控制。

而另一种主动控制方法则是机器人关节可动构件或关键部件中嵌入或者采用智能材料和智能结构，利用智能结构的特点实现机器人的振动主动控制，结构示意图，如图7所示。其中压电陶瓷以其频响高、质量轻、结构简单及价格便宜等特点在机器人振动控制中应用较为广泛。Chalhoub等[53]对一个由层压复合材料制造的机器人手臂的动态响应进行了研究，结果表明在高精密装配任务下，复合材料机器手可以减少振动和剪切变形对末端执行器轨迹的影响，提高了位置精度。Tzou等[54]应用压电陶瓷作为传感器和驱动器，对柔性机器人的弹性动力响应采取主动控制，取得了较好的抑制振动效果；Dadfarnia等[55]采用压电驱动器对机器手臂柔性梁的残余振动进行了控制，并利用基位移、手臂末端偏转和应变三个测量值评估控制效果，通过数值模拟和实验测试验证了该控制器的可行性。娄军强等[56]针对伺服电动机、谐波齿轮减速器、柔性臂及压电致动器组成的智能柔性机械臂系统，提出了对伺服电动机采用PD(Proportional Derivative)控制、对压电致动器采用模糊(Fuzzy)控制的复合控制策略。数值仿真和实验结果表明所提出的控制策略可行，柔性臂的振动衰减时间由6.5 s缩短为3.5 s，提高了柔性臂末端的定位控制精度。曹青松等[57]针对刚-柔-电耦合的双连杆压电柔性机械臂,提出基于模糊自整定PID算法的柔性臂振动主动控制方法。仿真及实验结果表明:模糊自整定PID控制器具有响应快、鲁棒性好、调整方便等优点,并更好地改善了控制系统的动态性能。

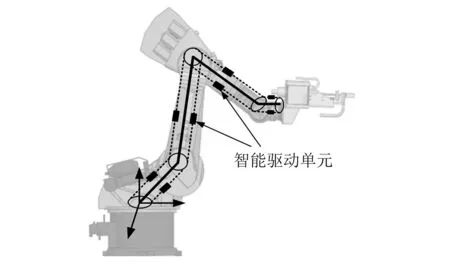
图7 机器人加工系统嵌入智能驱动单元示意图Fig.7 Diagram of embedded intelligent actuator unit for robot machining system

其他智能材料如形状记忆合金、电(磁)流变液、电致伸缩材料、磁致伸缩材料、光导纤维等在机器人振动控制中也有应用，如Baz等[58]研究了形状记忆合金作动器对机器人柔性梁结构的振动主动控制问题，实验表明形状记忆合金驱动器可以改变机器人结构的阻尼参数，并对控制性能和控制参数进行了评估和设计。Gandhi等[59]将电流变体应用于柔性机器人的振动控制，采用变分原理进行了电流变体驱动器的动态响应仿真，提高了机器人末端执行器的运动精度。戴金桥等[60]利用磁流变液在磁场作用下固液转换的快速、连续、可逆性能，提出了一种阻尼力连续可调的振动控制阻尼器，并应用与防化机器人肩关节振动的半主动控制，并进行了振动控制实验。

智能结构研究领域已有较多关于智能结构抑制机床切削颤振和机器人机械臂运动振动的研究，但在采用智能结构主动抑制机器人切削颤振研究上，还存在理论、建模、实验技术等各方面的欠缺。

4 结 论

综上对国内外研究现状的分析，机器人加工系统在航空、航天、汽车等机械加工制造业有着广阔的应用前景，为了保证其加工质量和加工稳定性，必须要解决机器人加工中切削颤振的问题。目前对机器人加工颤振的研究仍处于起步阶段，对其产生原因、动态特性、预测方法等还没有更为准确和科学的分析研究，揭示机器人加工系统的颤振机理，需要从机器人开链式多杆串联结构的动力学分析入手，阐明刚度、阻尼、质量等参数特性对颤振现象的作用机制。目前国内外针对机器人静刚度和动刚度目前已有了较为系统的研究，而针对机器人加工系统变结构和变刚度的特点，研究在切削力和压紧力等主要外部载荷共同作用下的系统刚度模型尚不多见，另外切削颤振现象与机器人刚度性能之间的关系仍需进一步深入研究。机器人动力学参数可以通过有限元法、最小二乘法、频响函数实验法、谐波法和模态实验法等方法进行辨识和实验验证。机器人加工系统的动力学建模方面需考虑机器人加工姿态和外部切削载荷作用，保证系统动力学特性参数的精度。

目前针对机器人加工切削颤振的研究还比较少，在颤振机理的理论模型和主动抑制的实验验证方面还存在欠缺；智能结构在其他振动控制领域已有成功应用，并具有独特优势，这为机器人加工颤振的主动抑制提供了解决思路，但智能结构与机器人加工系统的实现形式，以及加入智能结构主动控制后机器人系统动力学参数的变化对颤振的影响等问题还需要进一步研究和验证。随着航空航天以及智能材料技术的发展，以智能结构作为传感器和驱动器在机器人加工系统切削颤振主动控制领域必将具有广阔的应用前景。

[1] OLABI A R, BÉARÉÉ O, GIBARU M D. Feedrate planning for machining with industrial six-axis robots[J]. Control Engineering Practice, 2010,18(5):471-482.

[2] DEPREE J C. Gesswein, robotic machining white paper project-halcyon development [EB/OL].https:∥www.robotics.org/robotic-content.cfm?id=43.

[3] ODF R, BURLEY G, NAING S, et al. Error budgeting for assembly-centric design of aerostructures[J]. American Institute of Aeronautics and Astronautics, 2001,9(5):33-43.

[4] PAN Z, ZHANG H, ZHU Z, et al. Chatter analysis of robotic machining process[J]. Journal of Materials Processing Technology, 2006,173(3):301-309.

[5] World Robotics 2015 Industrial Robots [EB/OL]. http:∥www.ifr.org/industrial-robots/statistics.

[6] CHEN Y, DONG F. Robot machining: recent development and future research issues[J]. International Journal of Advanced Manufacturing Technology, 2013, 66(9/10/11/12):1489-1497.

[7] ATKINSON J, HARTMANN J, JONES S, et al. Robotic drilling system for 737 aileron[C]∥ SAE 2007 AeroTech Congress & Exhibition. Los Angeles, CA:SAE Technical Papers,2007.

[8] DEVLIEG, R, FEIKERT E. One-up assembly with robots[J]. Training, 2008, 2013:9-30.

[9] 曲巍崴, 董辉跃, 柯映林. 机器人辅助飞机装配制孔中位姿精度补偿技术[J]. 航空学报, 2011, 32(10):1951-1960. QU Weiwai, DONG Huiyue, KE Yinglin. Pose accuracy compensation technology in robot-aided aircraft assembly drilling process[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10):1951-1960.

[10] BI S, LIANG J. Robotic drilling system for titanium structures[J]. The International Journal of Advanced Manufacturing Technology, 2011,54(5/6/7/8):767-774.

[11] 公茂震, 袁培江, 王田苗, 等, 航空制孔机器人末端垂直度智能调节方法[J]. 北京航空航天大学学报, 2012, 38(10): 1400-1404. GONG Maozhen, YUAN Peijiang, WANG Tianmiao, et al. Intelligent verticality-adjustment method of end-effector in aeronautical drilling robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(10):1400-1404.

[12] ZHAO X, PAN Y, GAO F. Force-position hybrid control of a new parallel hexapod robot for drilling holes on fuselage surface[C]∥ ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, 2013:63-73.

[13] 王增翠, 秦现生, 白晶, 等. 飞机壁板自动制孔法向测量算法研究[J]. 机械设计与制造, 2014(6):160-163. WANG Zengcui, QIN Xiansheng, BAI Jing, et al. Research on normal measurement algorithm in auto-drilling of aircraft panel[J]. Machinery Design & Manufacture, 2014(6): 160-163.

[14] 王继虎, 刘长毅, 田威, 等. 机器人制孔工艺参数优化有限元仿真分析[J]. 南京航空航天大学学报, 2012, 44(B04):69-72. WANG Jihu, LIU Changyi, TIAN Wei, et al. Finite element analysis of robot drilling parameters optimization[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(B04):69-72.

[15] DEVLIEG R. High-accuracy robotic drilling/milling of 737 inboard flaps[J]. SAE Int J Aerosp, 2011, 4(2):1373-1379.

[16] SURDILOVIC D, ZHAO H, SCHRECK G, et al. Advanced methods for small batch robotic machining of hard materials[C]∥ Robotics; Proceedings of ROBOTIK 2012; 7th German Conference on. Munich:VDE,2012.

[17] KIHLMAN H, ERIKSSON I, ENNIS M. Robotic orbital drilling of structures for aerospace applications[C]. SAE Technical Paper, 2002.

[18] EGUTI C C A, TRABASSO L G. Design of a robotic orbital driller for assembling aircraft structures[J]. Mechatronics, 2014, 24(5):533-545.

[19] 谢祥南, 螺旋铣制孔设备孔径自动控制系统设计研究[D]. 杭州：浙江大学，2014.

[20] 单以才, 何宁, 李亮. 机器人化螺旋铣孔运动的矢量建模与仿真[J]. 计算机集成制造系统, 2014,20(3):612-617. SHAN Yicai, HE Ning, LI Liang. Vector modeling and simulation of robotic orbital drilling motion[J]. Computer Integrated Manufacturing Systems, 2014, 20(3):612-617.

[21] RAFIEIAN F, HAZEL B, LIU Z. Regenerative instability of impact-cutting material removal in the grinding process performed by a flexible robot arm [J]. Procedia Cirp, 2014,14:406-411.

[22] WANG W, YUN C.A path planning method for robotic belt surface grinding[J]. Chinese Journal of Aeronautics, 2011, 24(4):520-526.

[23] 张绍全. 工业机器人镗孔加工系统设计研究[D]. 杭州：浙江大学，2013.

[24] 曲巍崴, 侯鹏辉, 杨根军, 等. 机器人加工系统刚度性能优化研究[J]. 航空学报, 2013,34(12):2823-2832. QU Weiwai, HOU Penghui, YANG Genjun, et al. Reseach on the stiffness performance for robot machining system[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(12):2823-2832.

[25] QIHUI S, YANG W, QUAN Y, et al. Application of Siemens 840D on refitting of inner-milling Machine [J]. Manufacturing Technology & Machine Tool, 2005(3):120-122.

[26] PASHKEVICH A, KLIMCHIK A, CHABLAT D. Enhanced stiffness modeling of manipulators with passive joints[J]. Mechanism and Machine Theory, 2011, 46(5):662-679.

[27] ALICI G, SHIRINZADEH B. Enhanced stiffness modeling, identification and characterization for robot manipulators[J]. Robotics IEEE Transactions on, 2005, 21(4):554-564.

[28] ZHANG X, YANG W, CHENG X, et al. Stiffness identification for serial robot manipulator based on uncertainty approach[C]∥ Intelligent Robotics and Applications — International Conference. Aachen, Germany: Icira, 2011.

[29] DUMAS C, CARO S, GARNIER S, et al. Joint stiffness identification of six-revolute industrial serial robots[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(4):881-888.

[30] 朱健, 钻铆机械手钻孔过程的刚度分析[D]. 南京：南京航空航天大学，2013.

[31] LOPES A M. Complete dynamic modelling of a moving base 6-dof parallel manipulator[J]. Robotica, 2010, 28(5):781-793.

[32] MOHAN A, SINGH S P, SAHA S K. A cohesive modeling technique for theoretical and experimental estimation of damping in serial robots with rigid and flexible links[J]. Multibody System Dynamics, 2010, 23(4):333-360.

[33] QIN Z, BARON L, BIRGLEN L. A new approach to the dynamic parameter identification of robotic manipulators[J]. Robotica, 2010, 28(4):539-547.

[34] 静大海, 刘晓平. 机器人关节面时变物理参数在线识别的谐波传播法[J]. 机械工程学报, 2009, 45(3):296-301. JING Dahai, LIU Xiaoping. On-line identification of time-varying physical parameters of robot joint based on harmonic propagation[J]. Journal of Mechnical Engineering, 2009,45(3):296-301.

[35] ABELE E, WEIGOLD M, ROTHENBCHER S. Modeling and identification of an industrial robot for machining applications[J]. CIRP Annals-Manufacturing Technology, 2007, 56(1):387-390.

[36] 方强, 李超, 费少华, 等. 机器人镗孔加工系统稳定性分析[J]. 航空学报, 2016. 37(2): 727-737. FANG Qiang, LI Chao, FEI Shaohua, et al．Stability analysis of robot boring system[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2) :727-737.

[37] ÖZER A, EREN SEMERCIGIL S, PRASANTH KUMAR R, et al. Delaying tool chatter in turning with a two-link robotic arm[J]. Journal of Sound and Vibration, 2013, 332(6):1405-1417.

[38] MEJRI S, GAGNOL V, LE T P, et al. Dynamic characterization of machining robot and stability analysis[J]. International Journal of Machine Tools & Manufacture, 2016, 82(1/2/3/4):351-359.

[39] PAN Z, ZHANG H. Analysis and suppression of chatter in robotic machining process[C]∥ Control, Automation and Systems, ICCAS'07, 2007.

[40] HAZEL B, RAFIEIAN F, LIU Z. Impact-Cutting and regenerative chatter in robotic grinding[C]∥ ASME 2011 International Mechanical Engineering Congress and Exposition. 2011. American Society of Mechanical Engineers.

[41] GUO Y, DONG H, WANG G, et al. Vibration analysis and suppression in robotic boring process[J]. International Journal of Machine Tools & Manufacture, 2015, 101:102-110.

[42] BHUNGALIA A A, VELEY D E. Design of smart structures using bounded piezoelectrics[C]∥ AIAA, NASA, and ISSMO, 6th Symposium on Multidisciplinary Analysis and Optimization. Bellevue, WA, 1996.

[43] NARAYANAN S, BALAMURUGAN V. Finite element modelling of piezolaminated smart structures for active vibration control with distributed sensors and actuators[J]. Journal of Sound and Vibration, 2003, 262:529-562.

[44] HAN J H, REW K H, LEE I. An experimental study of active vibration control of composite structures with a piezo-ceramic actuator and a piezo-film sensor[J]. Smart Materials and Structures, 1997, 6:549.

[45] PRAKAH-ASANTE K O, CRAIG K C. The application of multi-channel design methods for vibration control of an active structure[J]. Smart Materials and Structures, 1994, 3:329-343.

[46] SEBASTIJANOVIC N, MA T W, YANG H T Y. Panel flutter detection and control using eigenvector orientation and piezoelectric layers[J]. AIAA Journal, 2006,45(1):118-127.

[47] ZHANG S, LI H, SCHMIDT R, et al. Disturbance rejection control for vibration suppression of piezoelectric laminated thin-walled structures[J]. Journal of Sound and Vibration, 2014, 333(5):1209-1223.

[48] 王民, 费仁元. 切削系统可变刚度结构及其颤振控制方法的研究[J]. 机械工程学报, 2009(增刊1):219-222. WANG Min, FEI Renyuan. Reseach of variable-stiffness structure and varying stiffness method of chatter control[J]. Journal of Mechnical Engineering, 2009(Sup 1):219-222.

[49] SILVA M M D, VENTER G S, VAROTO P S, et al. Experimental results on chatter reduction in turning through embedded piezoelectric material and passive shunt circuits[J]. Mechatronics, 2015, 29:78-85.

[50] DAVIS J H, HIRSCHORN R M. Tracking control of a flexible robot link[J]. IEEE Transactions on Automatic Control, 1988, 33(3):238-248.

[51] TSO S K, YANG T W, XU W L, et al. Vibration control for a flexible-link robot arm with deflection feedback[J]. International Journal of Non-Linear Mechanics, 2003, 38(1):51-62.

[52] SHIGANG Y. Weak-vibration configurations for flexible robot manipulators with kinematic redundancy[J]. Mechanism and Machine Theory, 2000, 35(2):165-178.

[53] CHALHOUB N G, GORDANINEJAD F, LIN Q, et al. Dynamic modeling of a laminated composite-material flexible robot arm made of short beams[J]. The International Journal of Robotics Research, 1991,10(5):560-569.

[54] TZOU H S, WAN G C. Distributed structural dynamics control of flexible manipulators—I. Structural dynamics and distributed viscoelastic actuator[J]. Computers & Structures, 1990, 35(6):669-677.

[55] DADFARNIA M, JALILI N, XIAN B, et al. Lyapunov-based piezoelectric control of flexible cartesian robot manipulators[C]∥ American Control Conference, 2003. Proceedings of the 2003. IEEE.

[56] 娄军强, 魏燕定, 杨依领, 等. 智能柔性机械臂的建模和振动主动控制研究[J]. 机器人, 2014(5):552-559. LOU Junqiang, WEI Yanding, YANG Yiling, et al. Modeling and active vibration control of an intelligent flexible manipulator system[J]. Robot, 2014(5):552-559.

[57] 曹青松, 周继惠, 黎林, 等. 基于模糊自整定PID算法的压电柔性机械臂振动控制研究[J]. 振动与冲击, 2010, 29(12):181-186. CAO Qingsong, ZHOU Jihui, LI Lin, et al. Vibration control of piezoelectric flexible manipulator based on fuzzy self-tuning PID algorithm[J], Journal of Vibaration and Shock, 2010, 29(12):181-186.

[58] BAZ A, IMAM K, MCCOY J. Active vibration control of flexible beams using shape memory actuators[J]. Journal of Sound and Vibration, 1990, 140(3): 437-456.

[59] GANDHI M V, THOMPSON B S, CHOI S B, et al. Electro-rheological-fluid-based articulating robotic systems[J]. Journal of Mechanical Design, 1989, 111(3):328-336.

[60] 戴金桥, 王爱民, 宋爱国. 基于磁流变液的柔性机器人振动控制阻尼器[J]. 机器人, 2010, 32(3): 358-362. DAI Jinqiao, WANG Aimin, SONG Aiguo. A magneto-rheological fluid based damper for vibration control of flexible robot[J]. Robot, 2010, 32(3):358-362.

Review on the research developments of robot machining systems and cutting chatter behaviors

WANG Zhanxi, ZHANG Xiaoyu, LI Feifei, ZHANG Shunqi, QIN Xiansheng

(School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

Applying industrial robot machining systems is a very efficient technical way for the assembly process in aviation and spaceflight fields. Because the rigidity of whole robot machining system is quite low, the chatter phenomenon may be stimulated by the periodic disturbance load in machining process, which may result in the processing failure, or even the machining system fracture. Therefore, the chatter phenomenon is a difficult technical problem which needs to be solved in the robot machining technology. In the paper, a review on the research of domestic and foreign advanced robot machining systems was presented. Focusing on the analysis of the main characteristics of robot machining systems and cutting chatter behaviors, it is expected to reveal the cutting chatter mechanism of robot machining systems based on the robot machining system stiffness model and dynamic model taken as the theoretical basis. In order to improve the machining precision of robot processing systems and the static and dynamic performances, it is expected to develop more suitable active devices for cutting chatter suppression. The further solution of the problems and future research directions were discussed.

robot machining system； cutting chatter； stiffness model； dynamic model； active suppression

国家自然科学基金项目(51505380)；陕西省科技统筹创新工程计划项目(2016KTZDGY06-01)；中央高校基本科研业务费项目(3102015BJ(II)CG014)

2016-05-25 修改稿收到日期： 2016-09-27

王战玺 男，博士，讲师，1983年生

秦现生 男，博士，教授，博士生导师，1962年生

TP242.2

A

10.13465/j.cnki.jvs.2017.14.024