可调谐局域共振梁带隙模型改进

陈圣兵， 王 刚

(1. 中国空气动力研究与发展中心， 四川 绵阳 621000；2. 湖南大学 机械与运载工程学院， 长沙 410082)

可调谐局域共振梁带隙模型改进

陈圣兵1， 王 刚2

(1. 中国空气动力研究与发展中心， 四川 绵阳 621000；2. 湖南大学 机械与运载工程学院， 长沙 410082)

局域共振声子晶体具有弹性波带隙特性，可用于结构振动与噪声控制。通过引入压电分流阵列也可以在基体结构形成弹性波带隙，尤其是谐振分流电路可以产生局域共振带隙。而且，通过调节分流电路参数可以方便地改变其局域共振带隙特性。研究了含压电分流阵列的局域共振梁带隙计算建模方法，指出了传统带隙模型的不足，并提出了改进模型。利用传递矩阵法计算了传统模型和改进模型弯曲波传播常数，比较了两种模型对带隙预测的差异，发现传统模型在局域共振带隙内形成了较大误差，利用改进模型可以大大提高局域共振带隙的预测精度。

超材料；压电分流；声子晶体；带隙

周期结构广泛存在于实际工程结构中，人们对周期性结构的研究有着悠久的历史[1-3]。Sigalas等[4]研究了球形散射体埋入某一基体材料中形成的三维周期性复合介质中弹性波的传播特性，首次从理论上证实了三维周期点振结构中存在弹性波带隙。Kushwaha等[5]在研究镍/铝二维固体周期复合介质时第一次提出了声子晶体的概念，类比光子晶体分析了声子完全带隙在理论研究中的意义。Martínez-Sala等[6]对西班牙马德里的一座具有百多年历史的雕塑进行了声学特性测试，该雕塑是由直径为2.9 cm的中空不锈钢圆柱周期性排布在一个4 m直径的圆形平台上，形成的晶格常数为10 cm，通过测试他们第一次从实验角度证实了弹性波带隙的存在。Liu等[7]将包覆软硅橡胶材料的铅球按立方晶格嵌入环氧树脂基体中形成了一种三维三组元声子晶体，理论和实验结果均表明该声子晶体带隙所对应的波长远大于晶格常数，由此提出了局域共振声子晶体的概念。近年来，局域共振声子晶体超常物理特性的揭示引起了大量学者的关注，并将这种具有超常物理特性的复合材料称为超材料，其特性包括带隙、负折射、负模量和声学斗篷等[8-10]。

含分流阵列的周期性压电复合结构也能够产生带隙，尤其是分流电路为谐振电路时能够产生可调谐局域共振带隙，可以通过电路参数的调节改变局域共振带隙特性。Thorp等[11]首次提出将压电分流技术应用于周期结构的带隙控制，研究了一维周期性分流杆中的弹性波传播的衰减和局域化。Thorp等[12]又利用周期性压电分流环来控制充液壳的波传播和衰减特性。Spadoni等[13]研究了含有谐振分流阵列薄板的波传播特性，得到了特定方向(ΓX)的弹性波带隙特性。Casadei等对此模型进行了实验研究，分析了不同电阻值和电感值对带隙的影响。Casadei等[15]研究了负电容和谐振电路共同对薄板振动的控制用，结果显示谐振电路在负电容的作用下得到了加强。Collet等[16]研究了二维压电分流阵列对铝板中波传播的影响，得出压电分流阵列对整体的波传播产生了大约17 dB的衰减。

本文作者及其合作者也对含有压电分流阵列的轻质结构进行了理论和实验研究，初步揭示了一维和二维压电分流阵列的带隙形成机理及其带隙特性[17-20]。尤其是在文献[19]中首次指出传统带隙模型在预测含有压电分流阵列一维杆中纵波带隙特性中存在的不足，并提出了改进建模方法。有关含有压电分流阵列梁中弯曲波带隙研究的文献中，关于分流电路的建模大多依然沿用了传统带隙模型[21-22]，因此本文进一步研究了含压电分流阵列梁的弯曲波带隙模型，指出了传统带隙模型在计算弯曲波带隙时也会存在较大误差，并提出了改进模型，提高了弯曲波带隙的预测精度。

1 带隙模型改进

1.1 物理模型

可调谐局域共振梁由三个部分构成：基体梁、压电片和分流电路，如图1所示。长度为lp的压电片分别粘贴在基体梁的上下表面，且每对压电片之间的距离都为l。基体梁厚度为h，宽度为b，压电片厚度为hp。压电片沿着厚度方向极化，并忽略粘贴层对结构的影响。每对压电片并联后与一个分流电路相连，分流电路由电阻R和电感L串联组成。

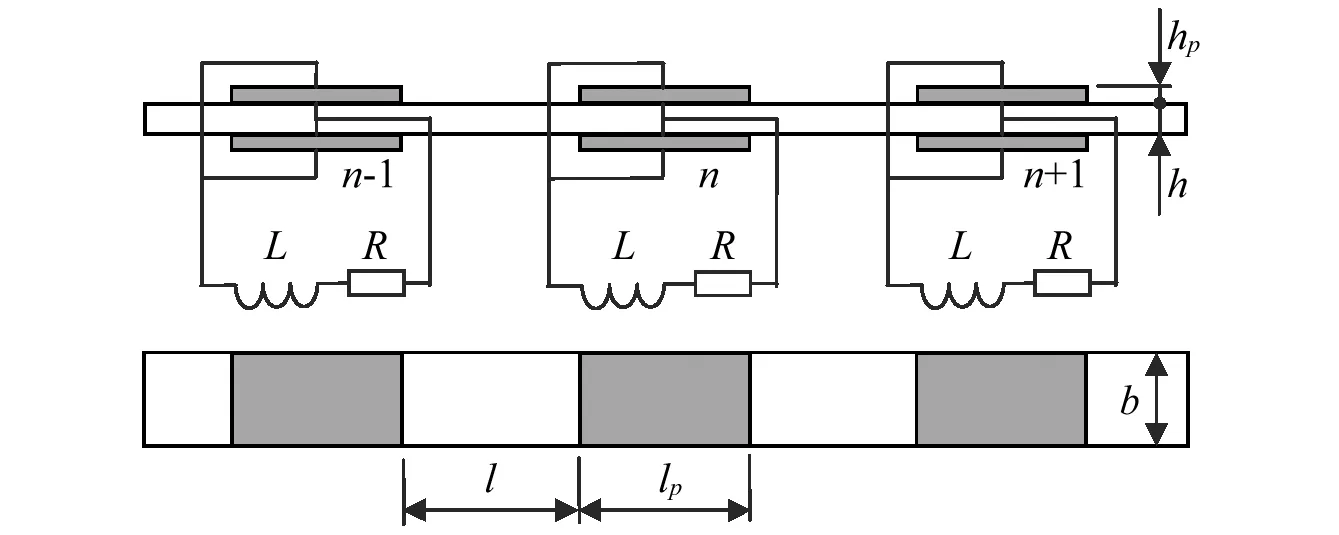
图1 可调谐局域共振梁示意图Fig.1 Sketch of the tunable locally resonant beam

由于每个分流电路和压电片参数都相同，所以该无限周期复合梁结构可以看作是由单个元胞(如图2所示)沿着轴向平移形成的一维超晶格结构。因此，只需要对单个元胞进行力学建模，并结合Floquet定理就可以得到整个梁中的波传播特性。

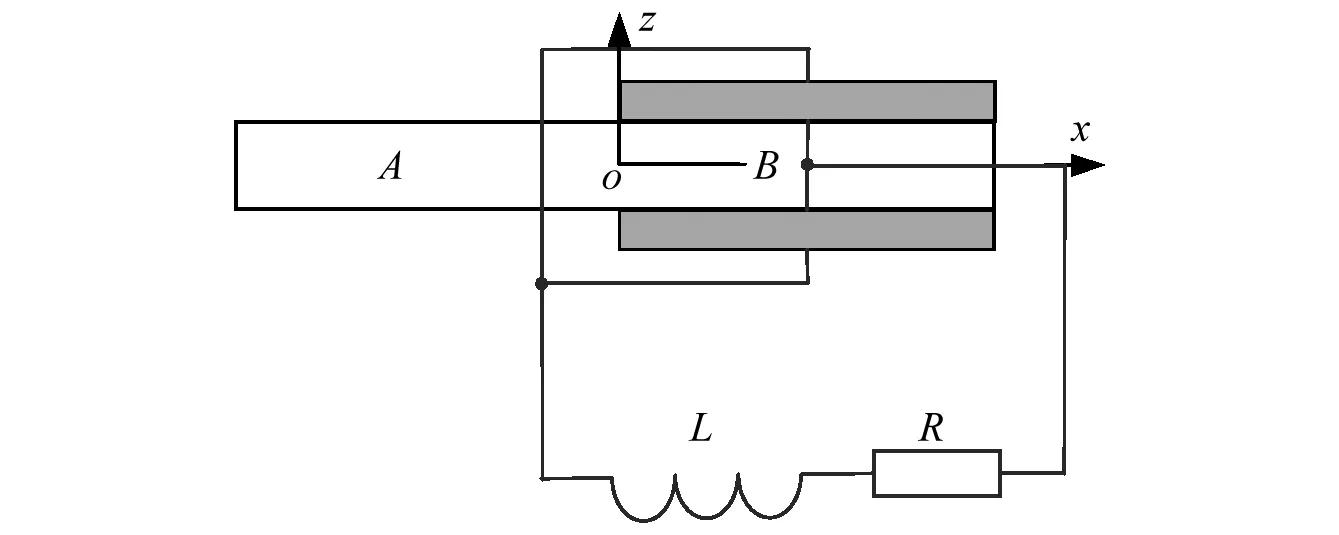
图2 元胞示意图Fig.2 Schematic of the cell

1.2 分流电路建模与改进

对于如图2所示的压电片和分流电路组成的压电分流系统，假设压电片除了垂直于x轴方向的端面外，其余表面都自由，且压电片只受到沿z轴方向的电场作用，那么简化后的d-型压电方程可以表示为

(1)

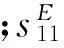
求解式(1)可得

(2)

(3)

由基本电路学公式，可得分流电路中电流可以表示为

(4)

式中:s为Laplace算子;V为压电片电极上的电势差;Q为电荷;Z=Ls+R为分流电路复阻抗。

而压电片内电场与电极上电势差之间的关系为

V=E3hp

(5)

式中:hp为压电片厚度。

将式(5)代入式(4)可得

(6)

传统模型假设压电内应变和电极上电位移处处相等，那么压电片电极上电荷表达式可以简化为

Q=D3As

(7)

式中:As为压电片电极的面积，且As=blp。

可见，传统模型得到的结果是建立在长波假设基础上的近似求解，因此其结果存在误差，并不能反映真实情况，而且这种误差随求解频率的增大而增加。

本文对传统模型进行改进，放弃长波假设，改用精确的积分模型代替，即电极上电荷Q为

(8)

那么将式(2)代入式(8)得

(9)

假设该周期性梁中仅传播弯曲波ψ(x,t)，则压电片在x处的应变可以分别表示为

(10)

将(10)式代入式(9)

(11)

联立式(6)和式(11)得

(12)

最后，再将式(12)代入式(1)可得

(13)

其中

(14)

而传统模型采用长波假设得到的应力表达式为

(15)

比较式(13)和(15)可以看出，改进模型和传统模型得到的结果存在较大差别：改进模型表明分流电路对压电片的作用等效为一个恒定的附加应力Ta，而不是传统模型得到的附加弹性模量。

1.3 基于传递矩阵法的弯曲波传播常数

对图2所示的元胞进行动力学建模，忽略剪切变形和截面绕中心轴转动惯量产生的影响，采用Euler-Bernoulli梁模型，其弯曲波控制方程为

(16)

式中:ψi(x,t)(i=1, 2)表示x处质点在t时刻的横向位移;下标1和2分别代表未贴压电片的梁段A和贴有压电片的梁段B，ξi可以表示为

(17)

式中:ρ、ρp和E、Ep分别为基体梁和压电片对应材料的密度和杨氏模量；A、Ap和I、Ip分别为基体梁和压电片的横面面积和截面惯性矩。

那么利用元胞内以及元胞间的边界连续性条件，包括位移、转角、弯矩和剪力连续，可以得到梁中弯曲波对应的传递矩阵T，其满足

ψn+1=Tψn

(18)

式中:ψn和ψn+1分别为n和n+1个元胞中弯曲波待定系数向量。

值得注意的是，通过模型的改进，分流电路的作用等效为附加应力，使得每对压电片对基体梁的作用等效为集中力偶M=TaAp(h+hp)。那么在边界条件中，弯矩连续条件要将该集中力偶考虑进去。

根据Floquet定理可知，周期结构中弹性波系数满足

ψn+1=eμψn

(19)

式中:μ为传播常数，其实部α为衰减常数，虚部β为相位常数。

因此，联立式(18)和式(19)可得

(T-eμ)ψn=0

(20)

即传播常数可以通过传递矩阵T的特征值求出。

当弯曲波的频率位于某些频率范围内时，衰减常数为零(α=0)，表明这些频率范围内的弹性波可以在梁中无衰减传播。而当衰减常数不为零(α≠0)时，则仅存在衰减传播模式，这些频率范围形成带隙。

2 结果与讨论

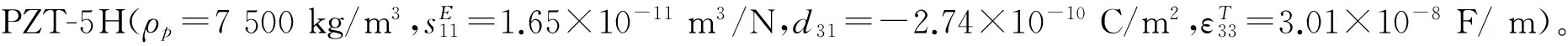
利用以上参数计算得到梁中弯曲波对应衰减常数如图3所示，其中电阻和电感的取值分别为R=20 Ω和L=50 mH。从图中可以看出，在0～2 kHz频率范围内出现了两个衰减区域(带隙)，其中第一带隙(FG)受到分流电路的影响较小，主要由压电片与基体间的阻抗失配引起，为布拉格带隙；第二带隙(SG)频率与分流电路的谐振频率强相关，主要由电路的谐振作用引起，为局域共振带隙。图中虚线(LM)和实线(IM)分别为传统模型和改进带隙模型得到的结果，可以看出两种模型得到的衰减常数在布拉格带隙和局域共振带隙中都产生了一定的差别，但局域共振带隙内的差异较布拉格带隙内显著很多。在布拉格带隙中，改进模型得到的带隙上边界频率比长波近似模型稍高(约9 Hz，占带隙宽度的3.6%)，而局域共振带隙中改进模型得到的衰减常数(约为0.49)比传统模型得到的值(约为0.90)要小很多，大约只有传统模型的一半多，其中最大衰减常数对应的频率也稍有不同(相差约43 Hz)。

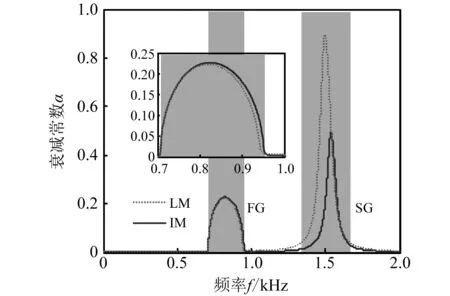
图3 衰减常数对比Fig.3 Comparison of attenuation constants

为了更进一步分析长波近似模型与改进模型相比产生的误差，首先不考虑阻尼产生的影响(R=0 Ω)，分别用两种模型计算不同电感L下布拉格带隙和局域共振带隙的带边频率，如图4所示。其中虚线和实线分别为传统模型(LM)和改进模型(IM)计算得到的结果，IM-L表示带隙下边界，IM-U表示带隙上边界。图4(a)为布拉格带隙，从图中可以看出，两种模型计算得到的布拉格带隙下边界频率基本一致，但带隙上边界频率却有较大差别。改进模型计算得到的上带边频率更高，从而导致预测的带隙宽度更大。而且随着电感L的增大，两种模型得到的结果在上边界频率处产生的差异增大。图4(b)为局域共振带隙，从图中可以看出，两种模型计算得到的局域共振带隙上边界频率差别较小，但带隙下边界出现了较大差异。传统模型计算得到的局域共振带隙下边界频率要比改进模型得到的结果低很多，使得该模型得到的带隙宽度较大。随着电感L的增大，两种模型在局域共振带隙下边界频率处产生的差异基本保持不变。总的来说，两种模型对带边频率位置的预测大体相同，尤其是带边频率随电感的变化趋势预测一致，但在数值上还是存在较大差异。

(a) 布拉格带隙

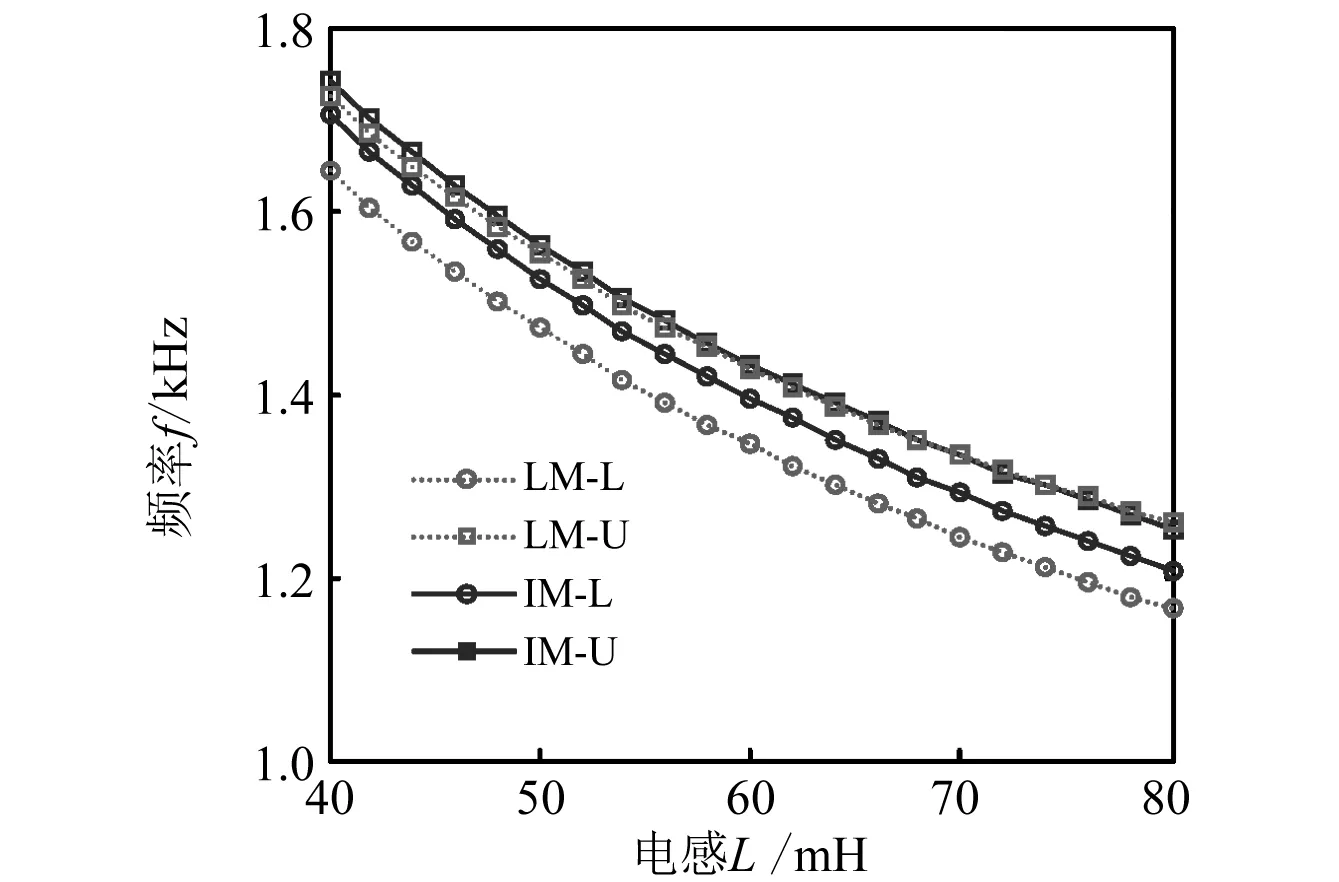
(b) 局域共振带隙图4 带边频率对比Fig.4 Comparison of bounding frequencies

采用两种模型计算得到的带隙内衰减随电阻R的变化如图5所示，其中电感取值L=80 mH，色谱代表衰减常数的大小。从图中可以看出对于布拉格带隙(第一带隙)，两种模型对布拉格带隙的预测结果较一致，随着电阻的变化，布拉格带隙内衰减常数的变化类似。而对于局域共振带隙，差别主要表现在传统模型得到的带隙内衰减明显大于改进模型得到的数值，由于改进模型结果更加符合真实情况，那么也就是说传统模型在预测局域共振带隙时得到的衰减常数误差较大。

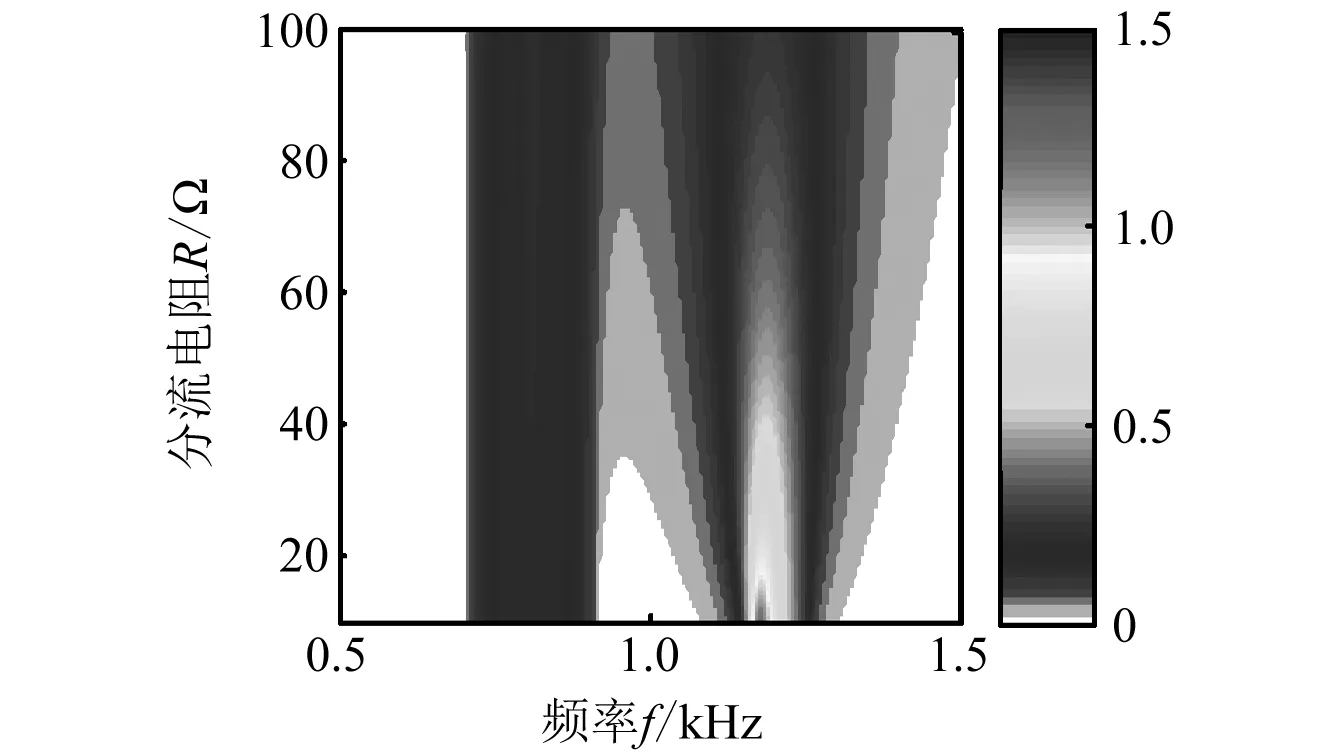
(a) 传统模型

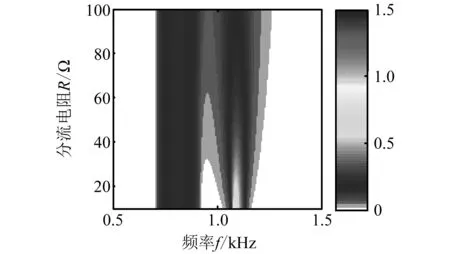
(b) 改进模型图5 不同模型的带隙内衰减对比Fig.5 Comparison of decay in the band gaps

3 结 论

本文指出了可调谐局域共振梁弯曲波带隙的传统建模方法存在的不足，并提出了改进模型。传统模型是建立在长波近似假设基础上，而改进模型采用了更加精确的积分建模，提高了带隙模型的精度。通过比较改进模型和传统模型得到的弯曲波传播常数差异，可以发现传统模型在局域共振带隙的预测上产生了较大误差。改进模型得到的局域共振带隙内衰减常数比传统模型得到的值要小很多，大约只有传统模型的一半多，其中最大衰减常数对应的频率也稍有不同。但随着分流电感的增大，两种模型在局域共振带隙下边界频率处产生的差异基本保持不变。

[1] MEAD D J. Free wave propagation in periodic-supported,infinite beams[J]. Journal of Sound and Vibration, 1970, 11(2): 181-197.

[2] MEAD D J, MARKUS S. Coupled flexural-longitudinal wave motion in a periodic beam[J]. Journal of Sound Vibration, 1983, 90(1): 1-24.

[3] MEAD D J. A new method of analyzing wave propagation in periodic structures: applications to periodic Timoshenko beams and stiffened plates[J]. Journal of Sound Vibration, 1986, 104(1): 9-27.

[4] SIGALAS M M, ECONOMOU E N. Elastic and acoustic wave band structure[J]. Journal of Sound Vibration, 1992, 158(2): 377-382.

[5] KUSHWAHA M S, HALEVI P, DOBRZYNSKI L, et al. Acoustic band structure of periodic elastic composites[J]. Physics Review Letter, 1993,71(13): 2022-2025.

[6] MARTINEZ-SALAR R, SANCHO J, SANCHEZ J V, et al. Sound attenuation by sculpture[J]. Nature, 1995,378: 241.

[7] LIU Z Y, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000,289: 1734-1736.

[8] LI J, CHAN C T. Double-negative acoustic metamaterial[J]. Physics Review E, 2004, 70(5): 055602.

[9] FANG N, XI D, XU J, et al. Ultrasonic metamaterials with negative modulus[J]. Nature Materials, 2006, 5(6): 452-456.

[10] MILTON G W. New metamaterials with macroscopic behavior outside that of continuum elastodynamics[J]. New Journal of Physcis, 2007, 9(10): 359.

[11] THORP O, RUZZENE M, BAZ A. Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches[J]. Smart Materials and Structures, 2001, 10(5): 979-989.

[12] THORP O, RUZZENE M, BAZ A. Attenuation of wave propagation in fluid-loaded shells with periodic shunted piezoelectric rings[J]. Smart Materials and Structures, 2005, 14(4): 594-604.

[13] SPADONI A, RUZZENE M, CUNEFARE K. Vibration and wave propagation control of plates with periodic arrays of shunted piezoelectric patches[J]. Journal of Intelligent Material System and Structures, 2009, 20: 979-990.

[14] CASADEI F, RUZZENE M, DOZIO L, et al. Broadband vibration control through periodic arrays of resonant shunts: experimental investigation on plates[J]. Smart Materials and Structures, 2010,19(1):015002

[15] CASADEI F, BECK B S, CUNEFARE K A, et al. Vibration control of plates through hybrid configurations of periodic piezoelectric shunts[J]. Journal of Intelligent Material System and Structures, 2012, 23(10):1169-1177.

[16] COLLET M, OUISSE M, ICHCHOU M N, et al. Semi-active optimization of 2D wave dispersion into shunted piezo-composite systems for controlling acoustic interation[J]. Smart Materials and Structures, 2012, 21: 094002.

[17] CHEN S B, WEN J H, YU D L, et al. Band gap control of phononic beam with negative capacitance piezoelectric shunt. Chinese Physics B, 2011, 20(1): 014301.

[18] CHEN S B, WEN J H, WANG G, et al. Locally resonant gaps of phononic beams induced by periodic arrays of resonant shunts. Chinese Physics Letter, 2011, 28(9): 094301.

[19] CHEN S, WEN J, WANG G, et al. Improved modeling of rods with periodic arrays of shunted piezoelectric patches[J]. Journal of Intelligent Material System and Structures, 2012, 23: 1613-1621.

[20] CHEN S, WANG G, WEN J, et al. Wave propagation and attenuation in plates with periodic arrays of shunted piezo-patches[J]. Journal of Sound and Vibration, 2013,332: 1520-1532.

[21] AIROLDI L, RUZZENE M. Wave propagation control in beams through periodic multi-branch shunts[J]. Journal of Intelligent Material System and Structures, 2011, 10: 1567-1578.

[22] AIROLDI L, RUZZENE M. Design of tunable acoustic metamaterials through periodic arrays of resonant shunted piezos[J]. New Journal of Physics, 2011, 13: 113010.

Band-gap model improvement for tunable locally resonant beams

CHEN Shengbing1, WANG Gang2

(1. China Aerodynamics Research and Development Center, Mianyang 621000, China；2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)

Locally resonant crystals possess elastic wave band-gaps, which can be used for vibration and noise control of structures. By introducing piezoelectric shunting arrays in host structures, band gaps can also be generated. Particularly, locally resonant gaps can be induced by resonant shunting circuits. Moreover, the properties of locally resonant gaps are conveniently tuned by modifying the circuit parameters. The modeling method for beams with piezoelectric shunting arrays was investigated, where the deficiency of the conventional model was pointed out and an improved model was proposed. By using the transfer matrix method, the propagation constants of the conventional and improved models were predicted and compared. The results demonstrate that the conventional model presents great errors. Hence, the improved model effectively boosts the accuracy of locally resonant gap prediction.

metamaterial; piezoelectric shunting; phononics; band gap

国家自然科学基金(51322502)

2015-12-28 修改稿收到日期： 2016-06-02

陈圣兵 男，博士，助理研究员，1984年10月生

TH113; O48

A

10.13465/j.cnki.jvs.2017.14.019