基于Lyapunov稳定性理论的星型耦合电动机网络的混沌同步

汪慕峰，韦笃取，罗晓曙，张 波，屈莉莉

(1.广西师范大学电子工程学院，广西 桂林 541004；2.华南理工大学电力学院，广州 510610;3.佛山科学技术学院自动化学院，广东 佛山 528000)

基于Lyapunov稳定性理论的星型耦合电动机网络的混沌同步

汪慕峰1，韦笃取1，罗晓曙1，张 波2，屈莉莉3

(1.广西师范大学电子工程学院，广西 桂林 541004；2.华南理工大学电力学院，广州 510610;3.佛山科学技术学院自动化学院，广东 佛山 528000)

基于Lyapunov稳定性理论和多个体协调控制，通过设计网络中互联电动机节点之间的耦合函数，实现整个星型耦合电动机网络的渐进同步。从理论分析和数值仿真两个方面，证明并验证了该控制策略的有效性。提出的耦合函数结构简单、控制效果良好，对保证电动机传动系统的协调同步运行具有较好的应用参考价值。

电动机网络；Lyapunov稳定性理论；多个体协调控制；混沌同步；永磁同步电动机

0 引言

永磁同步电动机(Permanent Magnet Synchronous Motor，PMSM)具有结构简单、效率高、体积小、高转矩、高速度等显著优点，因而在工业生产自动化的各个领域得以广泛应用。近年来，永磁同步电动机的稳定运行，特别是关于永磁同步电动机的混沌控制问题引起了人们的广泛关注，提出了许多有效的控制方法[1-3]。另一方面，现代工业自动化生产过程，如纺织、冶金、造纸、灌装液体药品等，需要多台电动机的协调来使生产得以正常运行，随着嵌入式与计算机网络测控等技术的发展，在运动控制、变频调速控制与伺服控制等系统中，将各种电动机引入网络控制的问题已成为了电动机传动领域研究的一个热点[4-5]。数量众多的电动机互联，在促进了自动化进程和提高了生产效率的同时，也使得电动机传动系统变得越来越复杂，进而对电动机传动系统的稳定性和可靠性的要求也越来越高。已有研究表明，单台PMSM在某些参数及工作条件下会出现混沌行为，使电动机系统发生故障[1-〗5]，主要外在表现为转矩和转速的间歇振荡、控制性能的不稳定、突发性或阵发性的病态机电振荡，系统不规则的电流噪声等。当电动机网络中某台或局部几台电动机由于混沌运动引发故障时，会通过积累、放大、扩散，对整个电动机传动系统产生极强的破坏力，并严重影响电动机网络的安全可靠运行[6-7]。而混沌同步是指系统的轨道收敛于系统轨道的同一值，使系统之间始终保持步调一致。因此，提出控制策略实现复杂电动机网络中的混沌同步，对电机传动系统整体的稳定运行具有重要理论价值和实际应用价值。

近年来，多个体协调控制的研究引起了众多领域学者的兴趣，如无线传感器网络[8]、多机器人系统[9-10]、无人驾驶飞机[11]、智能交通[12]等。作为多个体系统的协调控制中最基本的问题之一，一致性问题受到了科研工作者的广泛关注。在多个体系统中，一致性是指空间分布的多个个体在没有中央协调控制或者全局通信的情况下，个体之间通过局部的相互耦合作用，达到一个相同的状态或输出。目前，对于电动机网络的混沌同步控制问题的研究尚属少见。为此，本文以电动机组成的电动机网络作为一个多个体系统，建立节点数N=50和N=100的星型耦合电动机网络，基于Lyapunov稳定性理论和多个体协调控制，选取网络中第一个节点作为驱动系统，其他节点作为响应节点，通过电动机节点之间的耦合函数，实现整个星型耦合电动机网络的混沌同步。耦合函数结构简单、控制能耗少，在保证多电动机系统的稳定运行、提高工业生产效率方面具有较好的理论和应用参考价值。同时，当网络中电机数量增加时，依然会达到希望的控制效果，这对工业自动化中的大规模电机协同运行有重要参考价值。

1 基于Lyapunov稳定性理论和多个体协调控制的星型耦合网络同步

一致性是指多个体通过信息的共享与交互，实现某种状态的趋同[10]，其控制目标可描述为

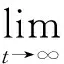
(1)

其中，Γ为系统中个体的集合，xi为系统中第i个个体的状态。

设一个任意的星型耦合网络由N个节点组成，第一个节点为主要节点。当不考虑其他N-1个节点与第一个节点之间的耦合连接时，网络中任一节点的动力学方程可表示为

(2)

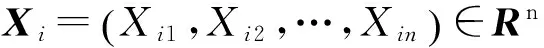
当其他N-1个节点与第一个节点之间耦合连接时，组成的网络系统可表示为

(3)

这里,Hij为互联节点之间的待定耦合函数，第一个节点不能与自身耦合，因此当i=1时，耦合函数为零。

利用一致性的概念，定义第一个节点与其他任意节点之间的状态变量误差为

(4)

则相应的误差系统为

(5)

此时，令

(6)

其中,ε>0是耦合强度。

那么有

(7)

要证明星型耦合网络系统(3)能否实现混沌同步，只要证明误差系统(5)在耦合函数的作用下能够实现渐进稳定。下面，提出定理1。

定理1 对于星型耦合网络系统(3)，选择网络中第一个节点作为驱动系统，其他节点作为响应系统。若其他节点与第一个节点之间的耦合函数可表示为式(7)，则星型耦合网络系统(3)中的其他节点可以实现与第一个节点的渐进同步。

证明：构造Lyapunov函数

(8)

结合式(5)，式(6)和式(7)，并沿式(8)的轨迹对时间求导有

根据Lyapunov稳定性理论，误差系统可以实现渐进稳定，也就证明了星型耦合网络系统(3)能够实现同步。证明完毕。

2 星型耦合电动机网络的同步

本文采用永磁同步电动机(PMSM)作为星型耦合电动机网络的节点，其无量纲数学模型表示为[13-14]：

(9)

其中，系统状态变量Iq，Id，ω分别表示q、d轴定子电流和转子角速度；系统参数σ、γ均为正值。Uq，Ud，TL为外部输入，分别表示q、d轴外加电压和外部扭矩。本文只考虑电动机工作在没有外部负载的情况下，即Uq=0，Ud=0，TL=0[13-14]。此时，PMSM的动力学方程可表示为

(10)

已有研究表明，当系统参数σ，γ在某些取值范围内时，PMSM会产生混沌振荡[1-5]。图1为系统参数σ=5.45，γ=20时，PMSM中的混沌吸引子。

研究发现，在PMSM为节点连接成复杂电动机网络中，随着随机性连边概率p的不断增加，整个电动机网络会出现混沌运动现象[6-7]。图2为节点数N=50，系统参数σ=5.45，γ=20，随机性连边概率p=0.5时，复杂电动机网络中任意一台PMSM的Lyapunov指数。可以看出，其最大Lyapunov指数大于零，说明存在混沌运动。当电动机网络中出现混沌运动，将会极大地影响电动机的稳定运行，甚至导致工业驱动系统的整体崩溃，给国民经济带来巨大损失。

图1 PMSM中的混沌吸引子Fig.1 Chaotic attractor in PMSM

图2 复杂电动机网络中任意一台PMSM的Lyapunov指数Fig.2 The Lyapunov exporents of any PMSM in complex motor network

因此，使用第一节中的控制策略来实现节点数为N的星型耦合电动机网络的混沌同步。

在模拟星型耦合电动机网络同步时，选择网络中的第一个节点PMSM系统作为驱动系统，剩余的N-1个节点PMSM系统作为响应系统，星型耦合网络连接如图3所示。这时，网络中第一个节点PMSM系统表示为

(11)

其余作为响应系统的节点PMSM系统表示为

(12)

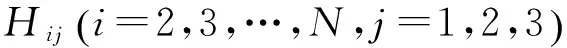
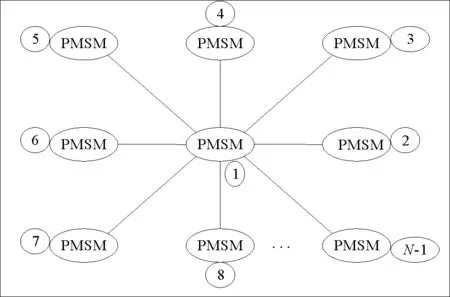
图3 星型耦合PMSM网络连接示意图Fig.3 Connection diagram of star coupled PMSM network

3 数值仿真

本节使用步长h=0.001的四阶Runge-Kutta公式解微分方程验证之前的理论分析。系统参数取σ=5.45，γ=20；各PMSM节点初始值随机选取。图4和图5分别为节点数N=50，耦合强度ε=0.5时，星型耦合电动机网络中各PMSM节点相应状态变量随时间的演化图和各节点之间相应状态变量误差随时间的演化图，其中e1=Iq1-Iqi，e2=Id1-Idi，e3=ω1-ωi，i=2,3,…,N。图6所示为节点数N=100，耦合强度ε=0.5时，星型耦合电动机网络中各PMSM节点相应状态变量随时间的演化图。图7所示为节点数N=50时，实现混沌同步所需时间t随耦合强度ε变化的曲线。从仿真结果可以看出，整个网络中所有的PMSM节点能够在很短的时间内实现渐进同步。而且，在节点数确定的情况下，实现同步所需的时间t会随着耦合强度ε的增大而减小。

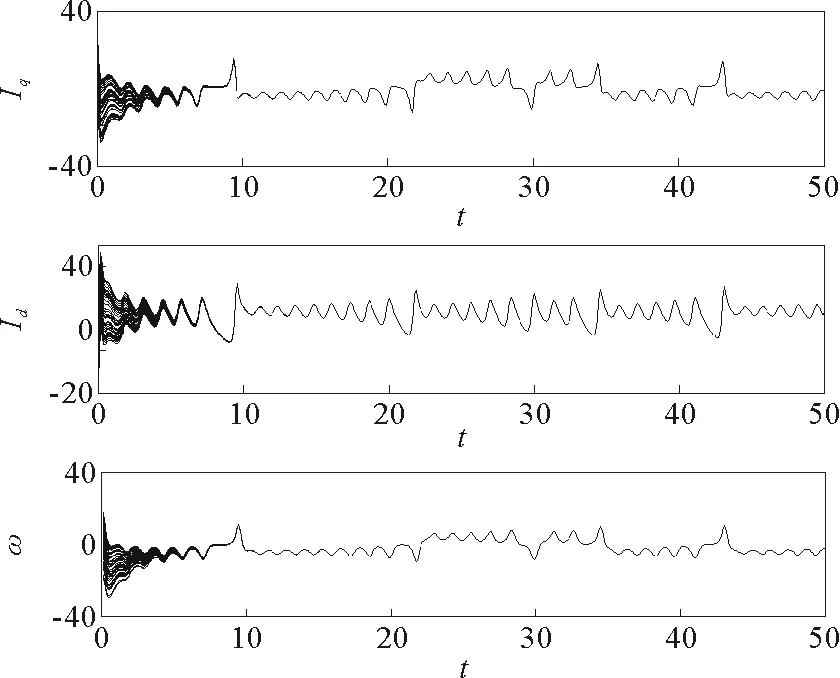
图4 N=50，ε=0.5时星型耦合复杂 PMSM网络中状态变量Iq、Id和ω的变化Fig.4 The evolution of state variable Iq、Id and ω in star coupled complex PMSM network when N=50, ε=0.5

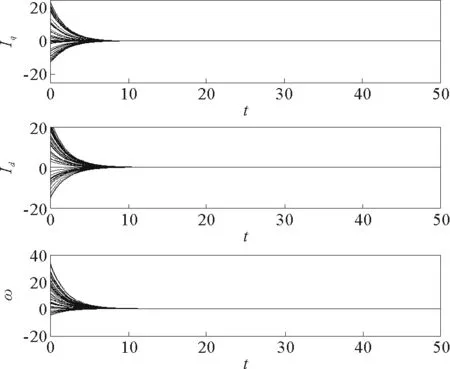
图5 N=50，ε=0.5时星型耦合复杂 PMSM网络中误差系统的变化Fig.5 The evolution of error dynamical system in star coupled complex PMSM network when N=50，ε=0.5

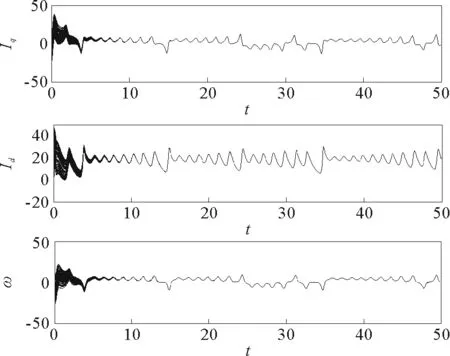
图6 N=100，ε=0.5时星型耦合复杂PMSM 网络中状态变量Iq、Id和ω的变化Fig.6 The evolution of state variable Iq、Id and ω in star coupled complex PMSM network when N=100，ε=0.5

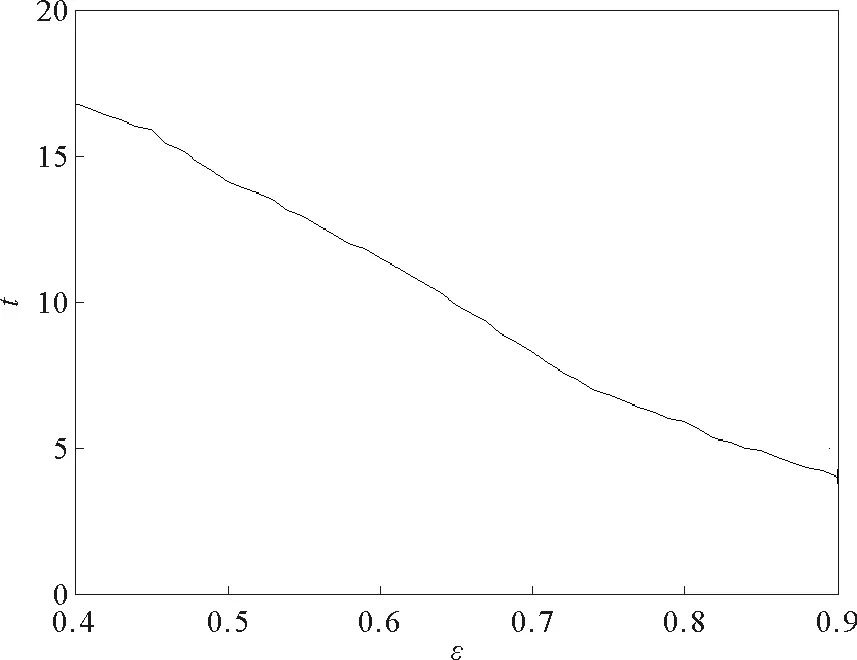
图7 N=50时控制时间t随 耦合强度ε增大的变化曲线Fig.7 The evolution currve of control time t with the increase of coupling strength ε when N=50

4 结语

本文基于Lyapunov稳定性理论，设计网络节点之间的耦合函数，实现了星型耦合电动机网络的渐进同步。通过理论推导证明和数值仿真验证，表明了控制策略不仅结构简单、控制时间短，而且控制效果良好。本控制策略通过任意选取一个节点作为驱动节点，能够实现整个电动机网络的整体同步，这对现代工业生产和工业自动化中的大规模电动机协同运行有重要参考价值。

[1]韦笃取, 张波. 基于无源性理论自适应镇定具有v/f输入的永磁同步电动机的混沌运动[J]. 物理学报, 2012, 61(3): 030505. Wei Duqu, Zhang Bo. Robust suppressing chaos in permanent magnet synchronous motor with v/f control based on passivity theory [J]. Acta Physica Sinica, 2012, 61(3): 030505.

[2]Wei D Q, Zhang B, Qiu D Y, et al. Effects of current time-delayed feedback on the dynamics of a permanent-magnet synchronous motor[J]. IEEE Trans Circ Syst II, Exp, 2010, 57(6): 456-460.

[3]于金鹏，于海生，高军伟，等。基于模糊逼近的永磁同步电机混沌控制[J]. 复杂系统与复杂性科学, 2013, 10 (4): 86-91. Yu Jinpeng, Yu Haisheng, Gao Junwei, et al. Chaos control of permanent magnet synchronous motors based on fuzzy-approximation[J]. Complex Systems and Complexity Science, 2013, 10 (4): 86-91.

[4]Blair D D, Jensen D L, Doan D R, et al. Networked intelligent motor-control systems[J]. IEEE Industry Applications Magazine, 2001, 7(6): 18-25.

[5]Walsh G C, Ye H. Scheduling of networked control systems[J]. IEEE Control Systems, 2001, 21(1): 57-65.

[6]Wei D Q, Luo X S, Zhang B. Chaos in complex motor networks induced by Newman-Watts small-world connections[J]. Chin Phys B, 2011, 20(12): 128903.

[7]Mai X H, Wei D Q, Zhang B, et al. Controlling chaos in complex motor networks by environment[J]. IEEE Trans Circ Syst Ⅱ, 2015, 62(6): 603-607.

[8]Lewis F L. A survey of linear singular system[J]. Syst and Signal Process, 1986, 5(1): 3-36.

[9]Liu B, Lu W, Chen T. Synchronization in complex networks with stochastically switching coupling structures[J]. IEEE Trans Autom Control, 2012, 57(3): 154-760.

[10] Zhao Y, Wen G, Duan Z. A new observer-type consensus protocol for linear multi-agent dynamical system[J].Asian J Control, 2013, 15(2): 571-582.

[11] Du H, Li S, Ding S. Bounded consensus algorithms for multi-agent systems in directed networks[J]. Asian J Control, 2013, 15(1): 282-291.

[12] Cheng L, Hou Z, Tan M. Decentralized adaptive consensus control for multi-manipulator system with uncertain dynamics[C]. Proc 2008 IEEE Int Conf on Systems, Man and Cybernetics, Singapore, 2008, 2712-2717.

[13] Hemati N, Kwatny H. Bifurcation of equilibria and chaos in permanent-magnet machines[C]. Proceeding of the 32nd Conference on Decision and Control, San Antonio, Texas, 1993: 475-479.

[14] Wei D Q, Zhang B, Luo X S, et al. Effects of couplings on the collective dynamics of permanent-magnet synchronous motors[J]. IEEE Trans Circuits Syst II Exp Briefs, 2013, 60(10): 692-696.

(责任编辑 耿金花)

Synchronizatin of Chaos in Star Coupled Motor Networks Based on Lyapunov Stability Theory

WANG Mufeng1, WEI Duqu1, LUO Xiaoshu1, ZHANG Bo2， QU Lili3

(1.College of Electronic Engineering, Guangxi Normal University, Guilin 541004, China;2.College of Electric Power, South China University of Technology, Guangzhou 510610, China;3.School of Automation, Foshan University，Foshan 528000, China)

The stability operation of the motor drive system is seriously affected when the motors in networks fall into chaotic motion. In this paper, coupling functions are designed to achieve asymptotically synchronization based on Lyapunov stability theory and coordination control of multi-agent. Theoretical analysis and numerical simulation results demonstrate the correctness and effectiveness of the proposed control strategy. This control strategy may play an important role in the stability operation of complex motor networks in industrial automation manufacturing.

motor networks; Lyapunov stability theory; coordination control of multi-agent; synchronization of chaos; permanent magnet synchronous motor (PMSM)

1672-3813(2017)02-0026-05；

10.13306/j.1672-3813.2017.02.004

2016-03-28；

2016-10-19

国家自然科学基金(11562004,61263021,51277030)

汪慕峰(1990-)，男，安徽宿州人，硕士研究生,主要研究方向为复杂电机系统及网络混沌控制。

韦笃取(1975-)，男，广西贵港人，博士，教授,主要研究方向为复杂电机网络动力学行为分析与控制。

O415

A