结合网络动力学的电网关键节点识别

傅 杰，邹艳丽，谢 蓉

(广西师范大学电子工程学院，广西 桂林 541004)

结合网络动力学的电网关键节点识别

傅 杰，邹艳丽，谢 蓉

(广西师范大学电子工程学院，广西 桂林 541004)

为了有效发掘出网络中的重要环节，提出了一种综合网络结构和节点动力学的电网关键节点识别方法，该方法结合两种已有的节点重要性评价指标——度中心性和接近中心性，同时定义和网络动力学相关的两个指标——临界同步耦合强度和失同步扩散时间。综合考虑4种性能指标的影响来确定节点的重要性，克服了单一评价指标的片面性，可以得到比使用单一评价指标更为准确的节点重要性评价结果。在IEEE14和IEEE57节点系统上进行仿真测试，实验结果验证了方法的合理性和有效性。

网络结构；动力学；电网；关键节点；同步临界耦合强度；失同步扩散时间

0 引言

随着电力网络研究的不断深入，人们从大量的统计数据中发现电力网络[1-2]中某些节点的故障会影响系统的正常运行，甚至会引发大停电事故[3-10]。因此，快速发掘出电力网络中的关键节点，对预防级联故障、提高系统的稳定性有着十分重要的指导意义。

经过长期的研究，学者们基于复杂网络理论，从网络拓扑结构、系统动力学、系统运行状态、功率输送关系、信息流传输、节点权重[11-20]等方面，提出了多种关键节点辨识方法。这些方法一般是针对某些特定问题提出来的，主要考虑的指标有节点与其他节点直接通信的能力、节点居于网络中心的程度、网络同步所花费的代价、失同步波扩散到整个网络的快慢程度、节点的全局影响力、节点对信息传输所做的贡献等，这些指标分别从不同的角度来说明节点的重要性，各自判断的侧重点有所不同，都有着一定的优点以及缺点。但是，众所周知现代电力网络结构错综复杂，根据单一指标对电网中的节点进行评价具有很大的片面性，很难有效地说明节点在电网中的重要程度。因此，需要利用多个指标，综合评价电力网络中各节点的重要性。

本文从复杂网络理论的角度出发，借鉴多属性决策思想[21]，同时考虑网络结构和节点动力学，对网络中节点的度中心性、接近中心性、临界同步耦合强度、失同步扩散时间4个指标进行综合评价，以确定电力网络中各节点的重要程度，在IEEE14和IEEE57节点标准测试系统上进行了仿真测试，实验结果表明了本文方法的有效性。

1 基于网络拓扑结构的评价指标

1.1 度中心性

节点i的度中心性DC(i)定义为节点i实际相连的边数与可能相连的最大边数的比率，其表达式为

(1)

其中，N为网络中的节点数，k(i)为与节点i直接相连的边数。度中心性表明了节点与其他节点直接通信的能力，一般认为其值越大，节点在网络中就越重要。

根据上述定义，计算出了IEEE14节点、IEEE57节点标准测试网络中各节点的度中心性，如图1所示。

图1 度中心性Fig.1 Degree centrality

1.2 接近中心性

节点i的接近中心性CC(i)定义为节点i到网络中其他节点的距离之和的倒数，其表达式为

(2)

其中，N为网络中的节点数，dij为节点i和节点j之间的最短路径。接近中心性表明了节点居于网络中心的程度，一般认为其值越大，节点在网络中就越重要。

根据上述定义，计算出了IEEE14节点、IEEE57节点标准测试网络中各节点的接近中心性，如图2所示。

2 基于动力学角度的评价指标

2.1 临界同步耦合强度

当电网中节点间的耦合达到一定的强度时，系统同步，把电网刚好能同步的耦合强度称作系统的临界同步耦合强度，用Kc表示。当电网中某一节点遭受攻击失效后，电网结构发生变化，令去除失效节点后最大连通子网的同步耦合强度为Kc′，其值越大，说明该节点失效后，剩余子网同步所花费的代价越大，则该失效节点在网络中的地位就越关键。

采用电网的类Kuramoto模型[22]，计算出了IEEE14节点、IEEE57节点标准测试网络中各节点失效后，剩余最大连通子网的临界同步耦合强度Kc′，如图3所示。

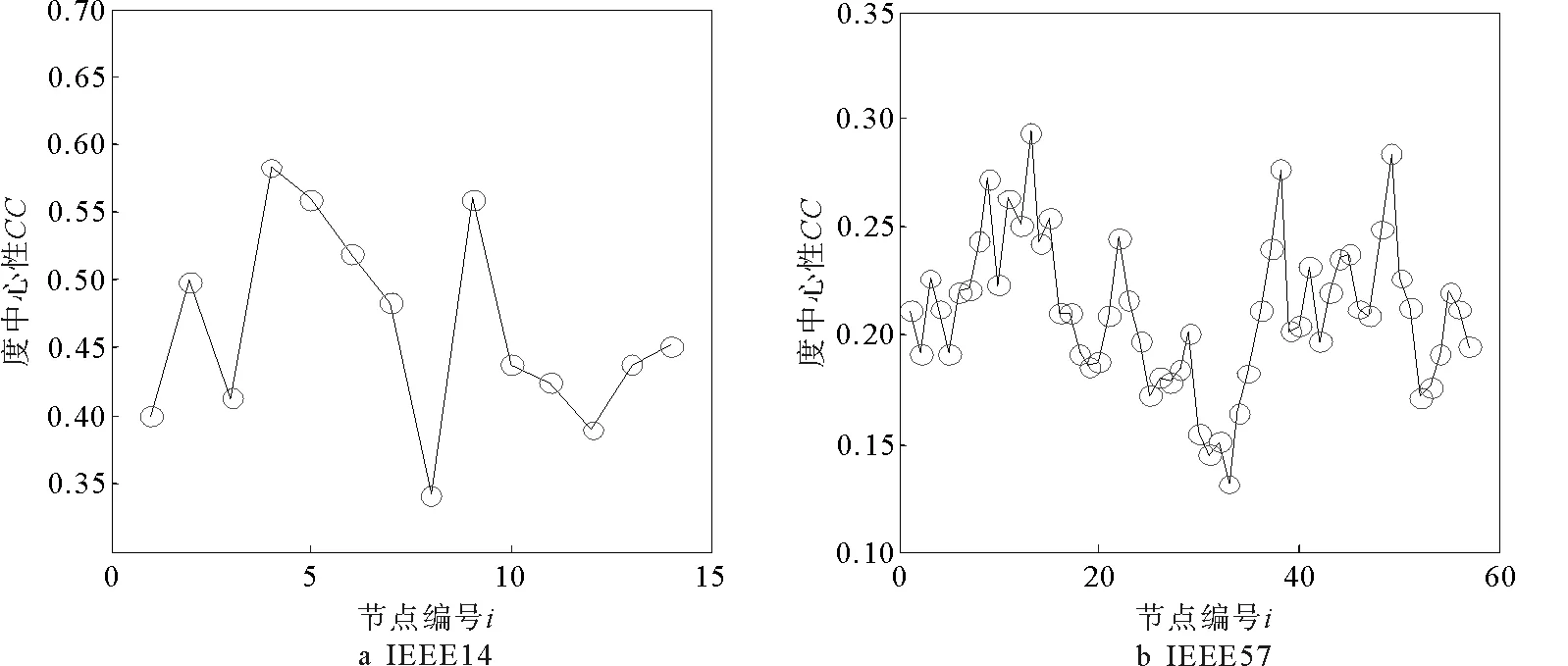
图2 接近中心性Fig.2 Closeness centrality

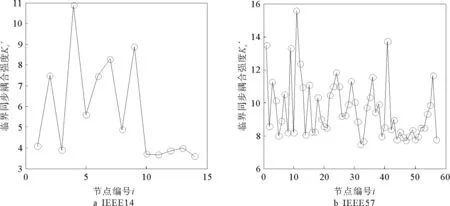
图3 临界同步耦合强度Fig.3 Synchronous critical coupling strength

2.2 失同步扩散时间

系统受到扰动后，受扰节点的频率最先开始偏离工作频率，然后拖动它的邻居节点的频率也偏离工作频率，继而影响更多的相邻节点，在不采取相应措施的情况下，级联失同步会扩散到整个网络。这里把失同步波从产生到扩散至整个网络的时间称为失同步波扩散时间，用T表示。这里为了方便后续研究，令T′=1/T。不同的节点受扰后，失同步波扩散到整个网络的时间不同，T越小，T′越大，说明节点对系统的稳定运行越重要，其在网络中的地位也就越关键。

采用电网的类Kuramoto模型，计算出了IEEE14节点、IEEE57节点标准测试网络中各节点受到扰动后，失同步波扩散到整个网络所需的时间T，如图4所示。

3 基于网络拓扑和动力学的综合评价方法

本文分别用4种不同的评价指标对电力网络中节点的重要性进行了评估，为了克服单一指标下评价结果的片面性，接下来将同时考虑上述4种指标，对电力网络中的关键节点进行综合评价。

首先，将度中心性、临界同步耦合强度、失同步扩散时间的倒数、接近中心性4种评价指标下的评价结果按列依次存放在矩阵X中，构成决策矩阵：

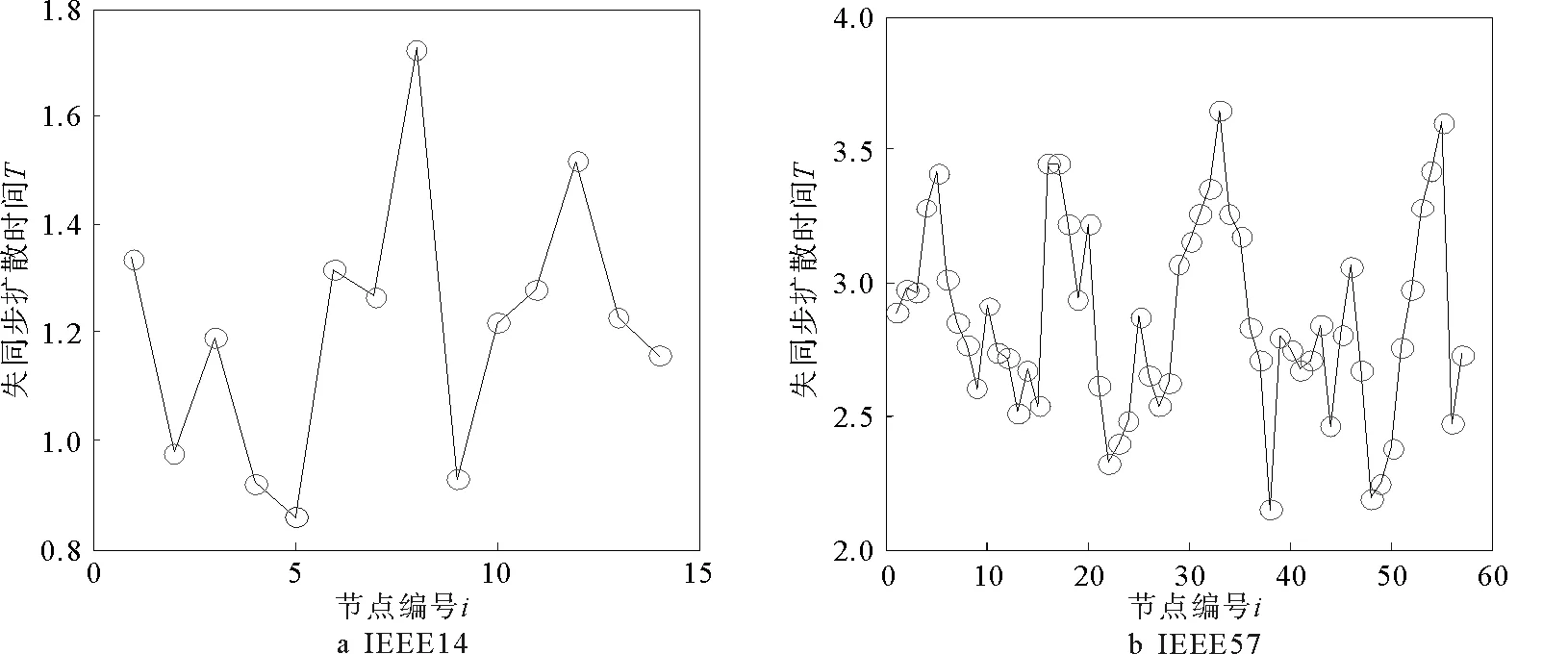
图4 失同步波扩散时间Fig.4 Time of de-synchronization wave diffusion

(3)

为了便于不同指标之间的比较，对决策矩阵进行归一化处理，即矩阵中的每个数值除以所在列的最大值：

rDC=xDC/xDC_maxrK=xK/xK_max

rT=xT'/xT'_maxrCC=xCC/xCC_max

(4)

得到归一化的决策矩阵：

(5)

然后，计算各指标的权重W，具体步骤如下：

1)采用三标度法，对上述4种指标进行两两比较后，建立比较矩阵A：

(6)

比较矩阵A的构建考虑了以下因素：

(1)度中心性涉及的网络结构因素最少，所以和其他指标相比重要性较差。

(2)最大连通子网的临界同步耦合强度和失同步波扩散时间相比，理论上很难对比两个指标的好坏，在矩阵A中给出了重要性相同的评价。此外，这两个指标均能表示节点对受扰或者失效后对最大连通子网的影响大小，其他两个指标无此功能，因此在构造比较矩阵A时，给这两个指标赋予了比其他指标重要性更高的值。

(3)接近中心性指标考虑了节点居于网络中心位置的程度，但并不涉及对其他节点的影响，故而其重要性略高于度中心性。

近年来，社区教育坚持“我生产什么，就卖什么”的卖方导向理念，基于“固本”文化所导致的守旧主义、功利主义比较严重，直接导致“社区教育重指令性活动的开展、轻社会效果和效益，重活动评比、轻活动质量，重行政评价、轻社会和个体评价等病灶仍然根深蒂固”［2］。社区家长教育既不能完善自身，又不能关照民意、关切民众实际需求，社区家长教育无法有效实施已是不争的事实。

2)用极差法构造判断矩阵C：

(7)

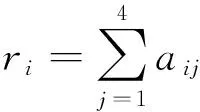
3)计算权重W：

(8)

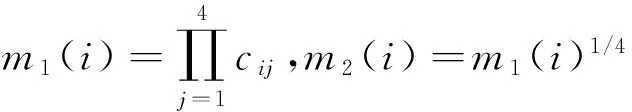
接下来，利用上述计算得到的权重W，和归一化的决策矩阵R一起构成加权的决策矩阵Y：

(9)

根据加权决策矩阵Y计算不同指标到正、负理想决策方案的距离：

(10)

其中，正理想决策方案yj_max为加权决策矩阵中第j列的最大值，负理想决策方案yj_min为加权决策矩阵中第j列的最小值。

最后，得到节点重要度的综合评价公式为

(11)

基于网络拓扑和动力学的综合评价方案的算法流程如图5所示。

图5 算法流程图Fig.5 Algorithm flow chart

按照本文提出的关键节点评价的综合方法，计算出了IEEE14节点、IEEE57节点标准测试网络中各节点的重要度(见图6)。

图6 综合方法获得的节点重要度Fig.6 The importance of nodes obtained by comprehensive method

4 仿真实验

由于尚不存在公认的检验电网节点重要性的方法，为了验证本文方法的可行性，分别移除IEEE14和IEEE57节点标准测试网络中的各个节点，对形成的最大连通子网的抗扰能力进行比较分析。一般认为，移除的节点越重要，则剩余子系统中，最大连通子网的稳定性及抗扰能力越差。

为方便后续仿真研究，根据第3节的实验结果，对IEEE14节点标准测试网络中各节点的重要度排序结果进行整理，如表1所示。

表1 IEEE14网络中各节点的重要度序号Tab.1 The importance of each node in the IEEE14 network

由于IEEE57节点标准测试网络中，节点数目过多，截取该网络中重要度最大的10个节点和重要度最小的10个节点，对其重要度排序结果进行整理，如表2所示，其中节点重要度序号1～10代表网络中重要度最大的10个节点，11～20代表重要度最小的10个节点。

表2 IEEE57网络中各节点的重要度序号Tab.2 The importance of each node in the IEEE57 network

接下来，按照表1和表2中节点重要度序号，分别移除网络中的节点，然后，对每次移除节点后形成的最大连通子网中的负荷节点施加扰动，观察最大连通子网可承受的最大扰动强度ΔPmax的变化情况。这里所说的的最大扰动强度是指最大连通子网中每个负荷节点所能承受的最大扰动强度。其中，每次移除节点后，系统的功率都进行重新分配，IEEE14节点标准测试网络中节点间的耦合强度K=12，IEEE57节点标准测试网络中节点间的耦合强度K=17。仿真实验结果如图7所示，图中横坐标表示节点重要度序号，纵坐标表示最大连通子网可承受的最大扰动强度ΔPmax。

图7 最大连通子网抗扰能力的变化情况Fig.7 The change of the anti-disturbance ability of the largest connected subnet

从图7可以看到，移除后形成的最大连通子网可承受的最大扰动强度ΔPmax最小的节点，其重要度排序总是最靠前的，这表明本文提出的重要度评价方法有效地辨识出了系统中最重要的节点。此外，通过观察可以得到，ΔPmax整体上随着被移除节点的重要度排序呈波动上升趋势，说明被移除节点重要度排序越靠前，去除该节点后，剩余最大连通子网可承受的最大扰动强度ΔPmax越小，即剩余子网稳定性越差，这表明本文方法辨识出了系统中的大部分关键节点。但同时也发现，图7中有少部分重要性居中的节点波动较大，通过最大连通子网的抗扰性比较，无法说明其重要度排序的准确性，这说明该检验方法尚存在一定的缺陷，这也是今后研究中需要进一步深入探讨的地方。综上所述，本文提出的关键节点评价方案是合理且可行的。

为了进一步验证本文提出的关键节点识别方法的有效性，对IEEE57节点标准测试网络，按照接近中心性、失同步扩散时间两种评价指标分别进行上述相同的仿真实验，结果如图8所示。

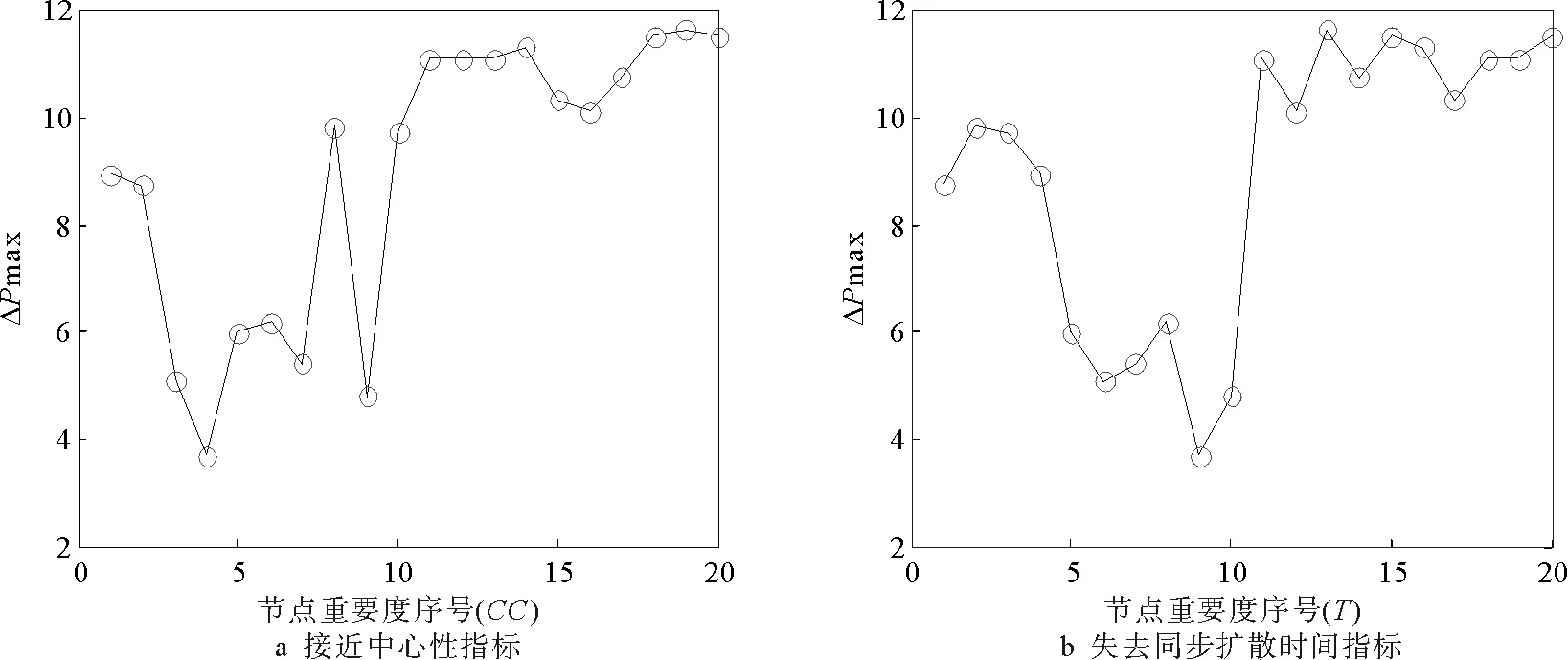
图8 最大连通子网抗扰能力的变化情况Fig.8 The change of the anti-disturbance ability of the largest connected subnet

从图8可以看到，在接近中心性、失同步扩散时间两种评价指标下，移除节点后形成的最大连通子网可承受的最大扰动强度ΔPmax最小的节点，其重要度并不是排在最前面的，这表明这类评价方法无法辨识出系统中最重要的节点。此外，通过进一步地观察还可以得到，在图8所示的两种方法下，ΔPmax整体上随着被移除节点的重要度排序呈现先下降后上升的趋势，而这与实际情况偏离较大，这表明此类方法评价出的关键节点并不完全合理。

通过以上的对比分析可以得知，本文提出的关键节点评价方法在一定程度上要优于现有的评价方法，因此，具有一定的合理性和可行性。

5 结语

电力网络中关键节点的识别研究对级联故障的防控具有重要意义。本文基于复杂网络理论知识，提出了一种综合考虑网络拓扑结构和系统动力学性能的关键节点辨识方法，克服了单一评价指标的片面性。利用决策矩阵将度中心性、临界同步耦合强度、失同步扩散时间、接近中心性4种评价指标进行综合考虑确定网络中节点的重要程度，在IEEE14和IEEE57网络上的抗扰性实验验证了本文提出的关键节点识别方法的有效性。

[1]Pagani G A, Aiello M. From the grid to the smart grid, topologically[J]. Physica A: Statistical Mechanics and its Applications， 2016, 449: 160-175.

[2]王光增, 曹一家, 包哲静，等. 一种新型电力网络局域世界演化模型[J]. 物理学报, 2009, 6: 3597-3602. Wang Guangzeng, Cao Yijia, Bao Zhejing, et al. A novel local-world evolving network model for power grids[J]. Chinese Journal of Physics, 2009, 6: 3597-3602.

[3]Conti J P. The day the samba stopped [power blackouts][J]. Engineering and Technology, 2010, 5(4): 46-47.

[4]Bhangu N S, Singh R, Pahuja G L. Reliability centred maintenance in a thermal power plant: a case study[J]. International Journal of Productivity and Quality Management. 2011, 7(2): 209-228.

[5]Park J W, Seol W C. Considerations for severe accident management under extended station blackout conditions in nuclear power plants[J]. Progress in Nuclear Energy, 2016, 88: 245-256.

[6]Aguiar A S, Lamego Simoes Filho F F, Alvim A C M, et al. Station blackout in unit 1 and analysis of the wind field in the region of Angra dos Reis[J]. Annals of Nuclear Energy. 2015, 78: 93-103.

[7]Watanabe T, Ishigaki M, Hirano M. Analysis of BWR long-term station blackout accident using TRAC-BF1[J]. Annals of Nuclear Energy 2012, 49: 223-226.

[8]Zeng B, Ouyang S, Zhang J, et al. An analysis of previous blackouts in the world: lessons for China′s power industry[J]. Renewable and Sustainable Energy Reviews, 2015, 42: 1151-1163.

[9]林伟芳, 汤涌, 孙华东,等. 巴西“2.4”大停电事故及对电网安全稳定运行的启示[J]. 电力系统自动化, 2011, 35(9): 1-5. Lin Weifang, Tang Yong, Sun Huadong, et al. Brazil “2.4” blackout accident and its implications for power system security and stability operation[J]. Automation of Electric Power System, 2011, 35(9): 1-5.

[10] 汤涌, 卜广全, 易俊. 印度“7.30”、 “7.31”大停电事故分析及启示[J]. 中国电机工程学报, 2012, 32(25): 167-174. Tang Yong, Bu Guangquan, Yi Jun. India “7.30” and “7.31” blackout accident analysis and revelation [J]. Proceedings of the CSEE, 2012, 32(25): 167-174.

[11] Hu J T, Du Y X, Mo H M, et al. A modified weighted TOPSIS to identify influential nodes in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 444: 73-85.

[12] Mo H M, Gao C, Deng Y. Evidential method to identify influential nodes in complex networks[J]. Journal of Systems Engineering & Electro-nics, 2015, 26(2): 381-387.

[13] Zhao J, Yu L, Li J R, et al. Identifying influential nodes based on graph signal processing in complex networks[J]. Chinese Physics B, 2015, 24(5): 58904-58913.

[14] Zhang T P, Fang B, Liang X Y. A novel measure to identify influential nodes in complex networks based on network global efficiency[J]. Modern Physics Letters B, 2015, 29(28): 1550168.

[15] Du Y, Gaoa C, Hub Y, et al. A new method of identifying influential nodes in complex networks based on TOPSIS[J]. Phys A, 2014, 399: 57-69.

[16] 刘彬, 王文吉, 李雅倩,等. 基于能量因素的无线传感器网络关键节点判定算法[J].电子与信息学报, 2014, 36(7): 1728-1734. Liu Bin, Wang Wenji, Li Yaqian, et al. Key nodes decision algorithm for wireless sensor networks based on energy factor [J]. Journal of Electronics & Information Technology, 2014, 36(7): 1728-1734.

[17] 张喜平, 李永树, 刘刚,等. 节点重要度贡献的复杂网络节点重要度评估方法[J]. 复杂系统与复杂性科学, 2014, 11(3): 26-32. Zhang Xiping, Li Yongshu, Liu Gang, et al. Evaluation method of complex network node importance based on node importance contribution[J]. Complex Systems and Complexity Science, 2014, 11(3): 26-32.

[18] 肖卫东, 谭文堂, 葛斌,等. 网络节点重要度的快速评估方法[J]. 系统工程理论与实践, 2013, 33(7): 1898-1904. Xiao Weidong, Tan Wentang, Ge Bin, et al. A fast evaluation method for the importance of network nodes[J]. Systems Engineering-Theory & Practice, 2013, 33(7): 1898-1904.

[19] 许立雄, 刘俊勇, 刘洋,等. 节点重要度的分类综合评估[J]. 中国电机工程学报, 2014, 34(10): 1609-1617. Xu Lixiong, Liu Junyong, Liu Yang, et al. Classification and synthesis evaluation of node importance[J]. Proceedings of the CSEE, 2014, 34(10): 1609-1617.

[20] 鞠文云, 李银红. 基于最大流传输贡献度的电力网关键线路和节点辨识[J]. 电力系统自动化, 2012, 36(9): 6-12． Ju Wenyun, Li Yinhong. Key lines and nodes identification of power network based on maximum transmission contribution degree[J]. Automation of Electric Power Systems, 2012, 36(9): 6-12．

[21] 于会, 刘尊, 李勇军. 基于多属性决策的复杂网络节点重要性综合评价方法[J].物理学报, 2013, 2(12): 1-8. Yu Hui, Liu Zun, Li Yongjun. Comprehensive evaluation method of complex network node importance based on multi attribute decision making[J]. Chinese Journal of Physics, 2013, 2(12): 1-8.

[22] Filatrella G, Nielsen A H, Pedersen N F. Analysis of a power grid using a kuramoto-like model[J]. European Physical Journal. B, 2008, 61(4): 485-491.

(责任编辑 李进)

Identification of Critical Nodes in a Power Network with Considering the Network Dynamics

FU Jie, ZOU Yanli, XIE Rong

(College of Electronic Engineering, Guangxi Normal University, The Guangxi Zhuang Autonomous Region Guilin 541004, China)

In this paper, in order to effectively discover the important links in a network, a method of identifying critical nodes in a power network is proposed, which is based on the network structure and the node dynamics. This method combines two kinds of existing node importance evaluation indicators, which are the degree centrality and the closeness centrality, at the same time, defines two evaluation indicators considering the network dynamics. The importance of a node is determined by comprehensive considering the influence of four kinds of evaluation indicators, which overcomes the one sidedness of single evaluation indicator, can get the more accurate node importance evaluation result than using single evaluation indicator. Simulation test on IEEE14 and IEEE57 node systems verifies the rationality and effectiveness of the proposed method.

network structure; dynamics; power networks; critical nodes; synchronous critical coupling strength; synchronous diffusion time

1672-3813(2017)02-0031-08；

10.13306/j.1672-3813.2017.02.005

2016-05-25；

2016-12-06

国家自然科学基金(11562003)；广西多源信息挖掘与安全重点实验室系统性研究课题基金(13-A-02-03);广西研究生教育创新计划项目资助课题(YCSZ2014098)

傅杰(1991-)，男，湖南岳阳人，硕士研究生，主研方向为复杂网络理论及其应用。

邹艳丽(1972-)，女，博士，教授，主要研究方向为非线性电路系统的混沌控制与同步、复杂网络的控制与同步。

TM711

A