互花米草克隆基株网络的随机游走特征

余艳泽,陈 希,李德志,韩定定

(华东师范大学 a.信息与科学技术学院，b.生态与环境科学学院，上海 200241)

互花米草克隆基株网络的随机游走特征

余艳泽a,陈 希a,李德志b,韩定定a

(华东师范大学 a.信息与科学技术学院，b.生态与环境科学学院，上海 200241)

基于野外实地调查的数据和复杂网络理论，分别定义4种形式的节点和4种类型的边，然后构建了具有异配性的互花米草基株多重关系网络。为了研究互花米草多重关系网络的拓扑结构和动态特性，建立了具有多个陷阱节点的随机游走模型。数值仿真结果显示：在随机游走过程中，无穗株丛和无穗分株是控制节点平均吸收时间的主要因素。经分析可知，建构的互花米草基株的水平空间扩散网络模式反映了其真实生境异质性模式。此外，该模型对于分析其它种类克隆植物的异质生境格局具有借鉴意义。

互花米草；随机游走；陷阱节点；生境异质性

0 引言

互花米草是一种典型的根茎型克隆植物，为了护滩固岸，它被从美国引入到中国沿海地区[1]。互花米草对中国很多沿海地区环境适应性强、繁殖速度快，很容易以特有的克隆网络形式大规模入侵到本地物种原有的生境中，造成本地物种的生境面积减少，甚至在某些区域出现一定程度的濒危趋势，导致入侵地生态系统的失衡和功能退化[2]，因此，探究互花米草在扩散生长过程中形成的克隆网络的特性及其生境格局间的协调关系，对于揭示其扩散入侵机理以及寻找有效的防治对策，具有重要的理论意义和实践应用价值。迄今，有关互花米草的研究文献非常丰富，内容主要包括：互花米草作为美国非土著地区外来入侵种的生长、生殖行为及在太平洋河口的扩散和防治[3-5]，互花米草促淤的作用[6-7]及其生理生态学特性[8-10]、互花米草入侵对大型底栖动物的影响[11]、基于生物学和生态学特性的互花米草控制和管理方法[12-14]、互花米草对稀疏生境的扩散[15]、环境胁迫对互花米草体内生物源二氧化硅的影响，不同生境互花米草叶内元素组成的比较[16]，芦苇与米草属植物在高氮、高盐水平生境内的相互作用[17]、互花米草的进化与近期杂交后果研究与评价[18-20]。

传统生态学的研究通常采用抽样调查的方法来获取互花米草基株的生长特征和生境异质性格局特征[21-22]，而生境异质性检测精度很大程度上又依赖于采样技术。然而，由于自然生境的复杂性和取样工作的艰巨性，导致这种方法不仅实行起来较为困难，而且即使实行，检测精度也较难保证。迄今为止，有关互花米草基株网络的拓扑结构动态特性的研究很少，这主要是因为互花米草在自然生境下生长模式非常复杂，很难获得其实际网络的完整数据，也很难用一般的生态学方法来分析。复杂网络作为一个强有力的数学工具，通常用于对具有复杂结构的系统进行建模。在复杂网络理论体系下，最终的研究目标是了解动态过程如何影响底层拓扑结构。

在过去的十年里，复杂网络上的随机游走算法广泛应用于各个科学领域，引起了研究者的大量关注。经典的陷阱问题，即以网络中的某个节点作为吸收节点,从其它非陷阱节点出发,以随机游走的方式到达陷阱节点,计算出这个过程所需的平均时间,进而可以得到网络结构特性与平均首达步长的关系[23]。陷阱问题中最重要的量是吸收时间(TT)，即首次到达时间(FPT)[24]，首达时间这个指标备受国内外学者关注[25-28]。首达时间表示从网络中预先选取好一个起始节点和一个陷阱节点,游走者从起始节点出发,等概率移动至邻居节点，最后首次到达陷阱节点的时间。而平均吸收时间(ATT)表示网络中全部的非陷阱节点到达陷阱节点所用时间的平均值，这通常是用来量化吸收过程效率的一个指标。目前为止，关于复杂网络随机游走的工作多是研究在固定位置上单一陷阱节点的情况，例如：对含有单个陷阱节点的网络输运效率的求解[29]，然而，鲜有研究多陷阱节点的情况，尤其是复杂网络中对模块化组织和无标度结构的多陷阱节点问题的研究存在空缺。但是，多陷阱节点网络通常具有现实意义，如克隆植物网络中的资源匮乏和竞争节点[30](这类节点的特性，如所处位置和强度大小等，对于具有生理整合特性的克隆植物网络的形成、发育的方向和速度以及竞争、扩散模式等，有着至关重要的影响)，资源匮乏节点实际上对应于随机游走过程中的多个吸收节点，也就是多陷阱节点，故而陷阱节点的选取方式对于随机游走具有重要的意义。

本文主要基于实证数据，采用复杂网络的方法构建了克隆植物互花米草基株的多重关系网络。基于此，探讨了具有多个陷阱节点随机游走网络的拓扑特征，并分析了互花米草基株竞争和扩散策略。最后，分析了互花米草基株网络与所处的异质性生境格局间的对应关系，从而提出了一种分析克隆植物生境异质性的新方法,解决或弥补了传统采用取样调查方法研究互花米草基株网络生境异质性格局的困难和不足。

1 数据获取与研究方法

1.1 数据获取

互花米草是一种多年生C4植物[31]。分株一般高1～3 m，叶长30～90 cm。互花米草主要通过根茎进行无性繁殖和种子进行有性繁殖[32]。每一分株可以产生多达600粒种子[33]。互花米草自20世纪70年代末被引入到上海东滩湿地后，由于其扩散速度快，如今已大面积分布在东滩湿地的低、中潮区。

调查地点位于长江河口的崇明岛东滩湿地(位于北纬31°25′～31°38′，东经121°50′～122°05′)。在潮间带湿地低潮区，土壤中的水分含量约为33%～39%，盐分的含量约为11～21 ppt[34]。随海拔的提高，土壤中的水和盐分含量呈逐渐减少的趋势。东滩湿地呈现出明显的植被带分区，按照从低到高的顺序，可以划分出光滩、以互花米草为主的群落、互花米草与芦苇混合区、以芦苇为主的群落。

在东滩湿地低潮区域，选择有互花米草稀疏分布的群落。选取3个相对独立的互花米草基株，尽可能完全地挖掘。当选择的互花米草目标基株与其它基株交互生长时，则切断其它基株的根茎，但尽量保留目标基株的完整性，包括地下根状茎和地上分株或株丛间的连接关系。当挖掘过程中某些部分断开时，采用化纤绳加以连接。当根茎伸入淤泥中太深时，则放弃对互花米草基株根茎的跟踪。通过整个过程，获取了3个具有可比性的而且相对完整的互花米草克隆基株。

1.2 研究方法

根据从东滩湿地挖掘出来的互花米草基株，分析其所在生境范围内的克隆基株网络空间构型。互花米草的基株由不同的部分组成，主要包括：株丛、分株(无穗分株、有穗分株)、根状茎。本文将互花米草基株在实际生长过程中形成的多级分枝结构作为复杂网络来研究，分析基株网络的结构和各组成部分之间关系。基于原始互花米草基株的空间构型网络，利用复杂网络构网的方法，建立合适的网络拓扑结构图，并且分析基株的所有生长指标单位。具有多重关系的互花米草基株网络连接规则为：1)节点：定义株丛为A类节点；无穗分株为B类节点；株丛间的根状茎节点作为C类节点；抽穗分株为D节点[35]。2)连边：定义抽穗分株间的根状茎连边为I型连边；株丛间的根状茎连边为II型连边；株丛内的分株之间的连边为III型连边；根状茎上无分株的节点之间的连边为IV型连边。

基于上述网络构建规则和定义，建立了3种具有多重关系的互花米草基株网络，这3种类型的网络分别为：BA无标度树状网络(网络1)、完全二叉树状网络(网络2)和小世界分形树状网络(网络3)。这3类网络不仅包含了互花米草基株物理结构上的连接，而且包含了作为基株构成部件之间的通信和生态关系，因此，这些网络能全面反映互花米草基株内的关系。

2 多陷阱树状网络随机游走算法

以随机变量族的描述方式作为出发点，以样本函数族作为描述方式，网络随机游走的问题即可转化为Markov求解过程[36]。复杂网络上的随机游走可以用两个节点i和j之间的转移概率表示。定义拉普拉斯矩阵中的元素为：游走节点和陷阱节点之间的转移概率。这样，复杂网络上的随机游走平均吸收时间的求解问题即转化为拉普拉斯谱的概率求解问题。为了更好地描述网络上随机游走的相关问题，基于无标度树状网络、完全二叉树状网络、小世界分形树状网络的构建原理，建立仿真模型。本文主要采用了3种不同的策略来选择互花米草基株网络的陷阱节点，即随机选取、按照不同类型的节点选取、按照节点度值来选取。

算法构建步骤为：

步骤1:初始化网络节点；

步骤2:构建网络邻接矩阵；

步骤3:按照陷阱节点选取规则，标记网络中的多个陷阱；

步骤4:从非陷阱节点出发进行随机游走；

步骤5:节点以相同概率游走，移动至下一个邻居节点；

步骤6:判断该节点是否是陷阱节点。如果是，则结束本次随机游走过程；否则，返回步骤5；

步骤7: 判断所有陷阱节点是否已经完成随机游走。如果是，则结束；否则，返回步骤4。

3 实验结果与分析

互花米草基株网络和其他很多实际网络具有一些共同属性。在互花米草基株多重关系网络中，皮尔森相关系数分别为-0.231 5、-0.241 4、-0.289 9，这体现了网络的异配性。一方面，新增节点倾向于连接具有度值较大的节点，反映了生境资源的不均匀分布，从而，可以断定网络的度分布服从幂律分布。另一方面，网络直径(即所有节点对之间最短路径距离的最大值)随网络规模扩大呈现对数增长，呈现小世界特性。此外，我们也能分析一些其它的网络特性，例如：邻谱等。下文主要从两个方面，对计算结果进行分析：平均吸收时间和陷阱节点关系、互花米草基株的生境异质性。

利用2中介绍的随机游走算法，对不同类型网络中的每组数据点，进行20次仿真模拟，取平均，得到随机游走过程中的平均吸收时间(ATT)等指标。

3.1 平均吸收时间(ATT)和陷阱节点关系分析

ATT和陷阱节点数服从幂律分布(如图1所示)，幂指数分别为：-1.462、-1.460和-1.532。每个网络分布的最佳拟合系数分别为：0.976 4、0.973 8和0.957 9。在互花米草基株网络中，生境资源匮乏的位点数目与分株生长受阻的个数呈现非线性相关。根据幂律分布的性质，随着陷阱节点数的增加，随机游走时间呈下降趋势，当达到阈值时，趋于平衡。这表明互花米草基株通过内在的信息传递机制，传达陷阱节点的信息，以此“警告”下一个分株躲避资源匮乏节点，避免出现资源稀缺。这有利于互花米草基株探寻和重建新的随机游走平衡路径。

基于多重关系网络连接规则，并从不同类型的节点中选取陷阱节点。图2展示了互花米草基株网络中，陷阱节点数和ATT之间的分布关系。当从A类节点中选取陷阱节点时，陷阱节点数和ATT的关系服从幂律分布。当从B，C，D类节点中选取陷阱节点时，陷阱节点数和ATT间的分布关系在其末端偏离幂律，但整体依然服从具有指数截断的幂律分布[36]。当陷阱节点数超过阈值时，ATT急速下降，这说明当以分株、根状茎或者抽穂节点作为陷阱节点时，随机游走过程中的陷阱节点超出一定范围，整个网络动力学特征会改变。当互花米草基株的分株、根状茎或抽穗节点停止生长时，整个基株可能会分散生长或者株丛之间会断绝联系。

该图为双对数坐标。陷阱节点为随机选择图1 互花米草基株网络随机游走平均吸收时间(ATT)和陷阱的节点数(nt)之间的关系Fig.1 Relationships between the average trapping time (ATT) and the number of trap nodes (nt) of the clonal network of Spartina alterniflora

该图为双对数坐标。陷阱节点从不同类型的节点中选择图2 互花米草基株网络平均吸收时间(ATT)和陷阱节点(nt)之间的关系Fig.2 Relationships between the average trapping time (ATT) and the number of trap nodes (nt) of the clonal network of Spartina alterniflora

在互花米草基株多重关系网络中，按照度值选取陷阱节点进行随机游走，且当网络中的陷阱节点从度值大于Kmin选取时，选取的陷阱节点Kmin和ATT分布如图3所示，呈现双段分布格局[35]；当陷阱节点的Kmin小于5时，平均吸收时间ATT基本不变。当Kmin大于5时，ATT和Kmin分布关系服从幂律分布，幂指数分别为2.102、1.677和1.86，每个网络分布的最佳拟合系数分别为0.957、0.921 2和0.907 5。在互花米草基株网络中，度值小于5的节点主要是根状茎上的无分株节点和抽穗分株节点，其它两类节点的度值均大于5。这表明，在互花米草基株网络随机游走的过程中，ATT的主要调控节点是A类和B类节点。在实际生境中，互花米草基株较大的株丛往往生长在资源相对较为丰富的小生境，这也体现了大株丛在整合网络中的决定性作用。

该图为双对数坐标图3 互花米草基株网络平均吸收时间(ATT)和最小度值(Kmin)的分布关系Fig.3 Relationships between the average trapping time (ATT) and the minimum degree (Kmin) of trap nodes of the clonal network of Spartina alterniflora

3.2 互花米草的生境异质性分析

互花米草基株网络中的无穗分株数服从指数分布(如图4a，5a、6a所示)，每个网络分布的最佳拟合系数分别为0.903 1，0.895 5和0.871 4。当株丛含有大量的分株时，株丛概率分布趋于平衡。聚集在小生境上分株的数量反映了土壤养分斑块规模。分株数量呈指数分布说明生境斑块规模的分布具有相似性，这表明土壤资源的主要特征呈异质性：在生境中，小而肥沃斑块数多于大而肥沃斑块数。

互花米草基株根状茎节数分别服从指数为-3.526、-3.9071和-3.165的分布(如图4b、图5b、图6b所示)，网络分布的最佳拟合系数分别为0.957 1，0.953 9和0.930 4。根状茎节数在一定程度上可以反映互花米草基株生境异质性格局的纹理特性，即根状茎的长度越大，纹理越粗。根据根状茎节点数的分布特点，这些生境异质性格局纹理的主要特征表现出相反的模式(如图4b、图5b、图6b所示)，即服从稀疏模式的幂律分布。

抽穗比例和抽穗分株数均服从指数分布(如图4c，4d，5c，5d，6c，6d所示)。每个网络抽穗比例分布的拟合系数分别为0.926 9，0.928 1和0.947 5；每个网络抽穗分株分布的拟合系数分别为0.993 5，0.987 3和0.991 1。互花米草基株繁殖的主要方式是克隆繁殖，而当小生境中的资源相对丰富时，则可以呈现有性繁殖。从某种意义上说，抽穗分株数量可以反映生境资源的丰富程度。整个基株株丛数量主要服从指数分布，它刻画了生境异质性模式的强度。

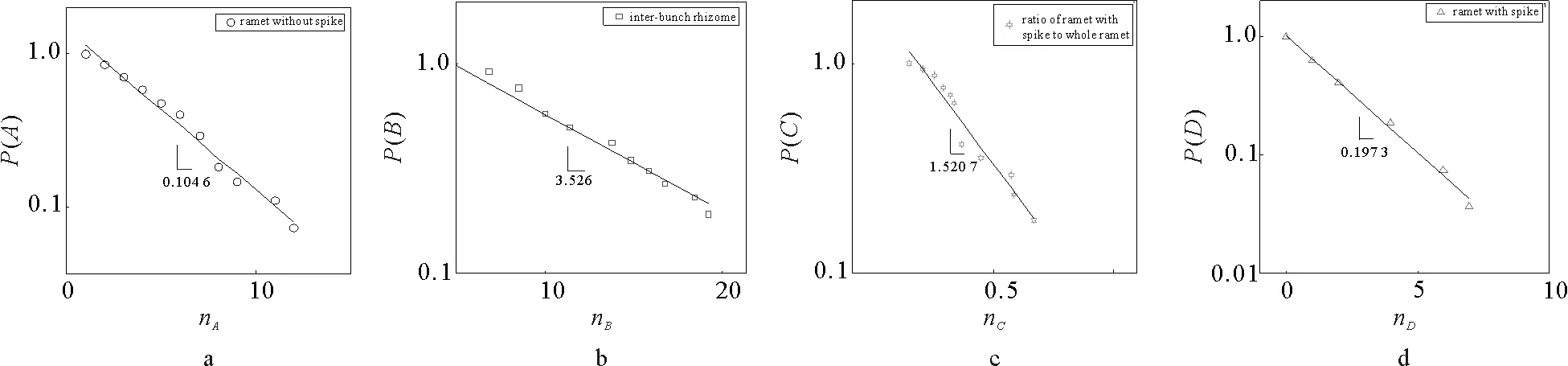
a、c、d是单对数坐标下的累积概率分布，b是双对数坐标下的累计概率。图4 互花米草基株网络1的累积概率分布图Fig.4 The distributions of the accumulated probability of the clonal network 1 of Spartina alterniflora

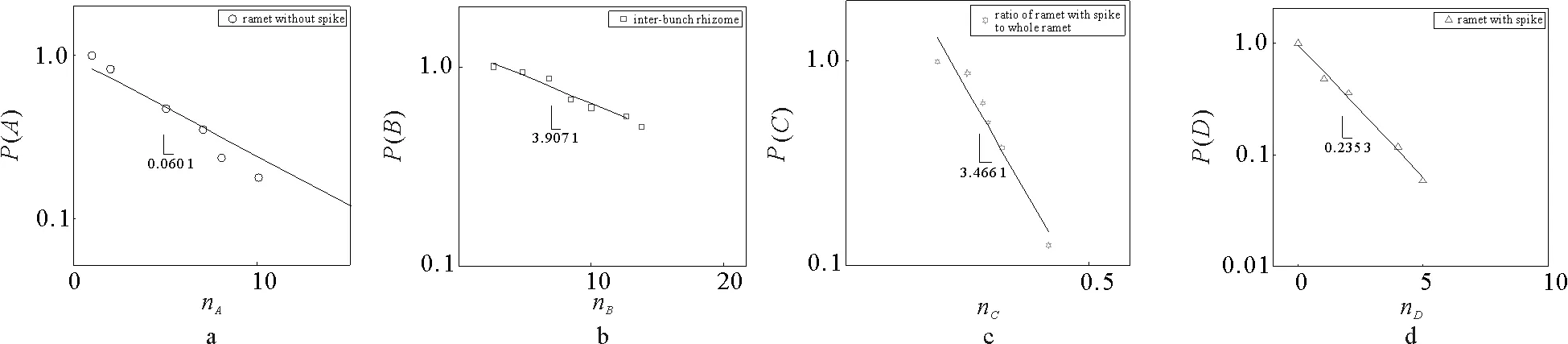
a、c、d是单对数坐标下的累积概率分布，b是双对数坐标下的累计概率。图5 互花米草基株网络2累积概率分布Fig.5 The distribution of the accumulated probability of the clonal network 2 of Spartina alterniflora

a，c，d是单对数坐标下的累积概率分布，b是双对数坐标下的累计概率。图6 互花米草基株网络3累积概率分布Fig.6 The distribution of the accumulated probability of the clonal network 3 of Spartina alterniflora

4 结论

本文通过构建具有多重关系的克隆植物互花米草基株网络，对网络拓扑结构和动态特性进行了分析，最终得到如下结论：1)互花米草基株多重关系网络呈现异配性。新增节点倾向于连接度值较大的节点，随机游走时间和陷阱节点之间的关系服从幂律分布。根据幂律分布的特点，随着陷阱节点数目增加，随机游走时间下降，当达到阈值时，趋于平衡。互花米草的克隆整合特性能使分株在一定程度上避免资源稀缺，对于随机游走过程而言，有助于重建一个新的平衡方式；2)随机游走时间和A型节点之间的数目关系服从幂律分布；随机游走时间和B、C、D型节点数目之间服从具有指数截断的幂律分布，当陷阱的节点数量超过阈值时，随机游走时间迅速下降；3)在随机游走过程中，主要调控节点随机游走时间的是无穗株丛和分株数；4)互花米草基株网络的水平空间扩散模式反映了其真实生境异质性模式。聚集在小生境上的分株数量反映了土壤养分的斑块尺度，并且小而肥沃的生境斑块数多于大而肥沃的生境斑块数。互花米草基株根状茎间隔节点长度服从幂律分布，反映了湿地生境异质性模式的纹理特性，这一特征服从具有稀疏模式的幂律分布。有穗分株数所占的比例和有穗分株数都服从指数分布，反映了生境资源丰富程度。整个基株株丛数量的分布服从指数分布，刻画了生境异质性模式的强度。

本文提出的方法不仅得到互花米草基株自身的生态学特性、扩散生长特性以及株丛间彼此间回避竞争的生态学策略，而且克服了通过传统釆样方法获取互花米草生境异质性格局特征的困难，体现了复杂网络的理论和方法在该分析中的独特价值。

[1]Metcalfe W S, Ellison A M, Bertness M D. Survivorship and spatial development of Spartina alterniflora Loisel. (Gramineae) seedlings in a new England salt marsh [J]. Annals of Botany, 1986, 58(2): 249-258.

[2] Simenstad C A, Thom R M. Spartina alterniflora (smooth cordgrass) as an invasive halophyte in pacific northwest estuaries [J]. Hortus Northwest, 1995, 6(1): 9-12, 38-40.

[3]Daehler C C, Strong D R. Variable reproductive output among clones of Spartina alterniflora (Poaceae) invading San Francisco Bay, California: the influence of herbivory, pollination, and establishment site[J]. American Journal of Botany, 1994, 81(3): 307-313.

[4]Daehler C C, Strong D R. Status, prediction and prevention of introduced cordgrass Spartina spp. invasions in Pacific estuaries, USA[J]. Biological Conservation, 1996, 78(1/2): 51-58.

[5]Burger J. Nesting behavior of Herring Gulls: invasion into Spartina salt marsh areas of New Jersey[J]. Condor, 1977, (2): 162-169.

[6]Craft C, Reader J, Sacco J N, et al. Twenty-five years of ecosystem development of constructed Spartina alterniflora (Loisel) marshes[J]. Ecological Applications, 1999, 9(4): 1405-1419.

[7]Ranwell D S. Spartina salt marshes in southern England. II. Rate and seasonal pattern of sediment accretion. III. Rates of establishment, succession and nutrient supply at bridgwater bay, somerset[J]. Journal of Ecology, 1964, 52(1): 79-94.

[8]Mendelssohn I A, McKee K L, Patrick W H. Oxygen deficiency in Spartina alterniflora roots: metabolic adaptation to anoxia[J]. Science, 1981, 214(4519): 439-41.

[9]Teal J M, Kanwisher J W. Gas transport in the marsh grass, Spartina alterniflora[J]. Journal of Experimental Botany, 1966, 17(2): 355-361.

[10] Bradley P M, Morris J T. Influence of oxygen and sulfide concentration on nitrogen uptake kinetics in Spartina alterniflora[J]. Ecology, 1990, 71(1): 282-287.

[11] Hedge P, Kriwoken L K. Evidence for effects of Spartina anglica invasion on benthic macrofauna in little swanport estuary, Tasmania[J]. Austral Ecology, 2000, 25(2): 150-159.

[12] Wang Q, An S, Ma Z, et al. Invasive Spartina alterniflora: biology, ecology and management[J]. Acta Phytotaxonomica Sinica, 2005, 44(5): 559-588.

[13] Nehring S, Hesse K J. Invasive alien plants in marine protected areas: the Spartina anglica affair in the European Wadden Sea[J]. Biological Invasions, 2008, 10(6): 937-950.

[14] Dennis B, Civille J C, Strong D R. Lateral spread of invasive Spartina alterniflora in uncrowded environments[J]. Biological invasions, 2011, 13(2): 401-411.

[15] Querné J, Ragueneau O, Poupart N. In situ biogenic silica variations in the invasive salt marsh plant, Spartina alterniflora: a possible link with environmental stress[J]. Plant and Soil, 2012, 352(1/2): 157-171.

[16] Tobias V D, Williamson M F, Nyman J A. A comparison of the elemental composition of leaf tissue of Spartina patens and Spartina alternifora in Louisiana's coastal marshes[J]. Journal of Plant Nutrition, 2014, 37(8):1327-1344.

[17] Arthur M L. A competitive interaction and dominance experiment between the vegetative marsh species phragmites australis and Spartina cynosuroides under elevated nitrogen and salinity levels[D]. Maryland：University of Maryland, 2013.

[18] Ainouche M, Chelaifa H, Ferreira J, et al. Erratum From—Polyploid Evolution in Spartina: Dealing with Highly Redundant Hybrid Genomes[M]. Polyploidy and Genome Evolution. Springer Berlin Heidelberg, 2012: 225-243.

[19] Salmon A, Ainouche M L, Wendel J F. Genetic and epigenetic consequences of recent hybridization and polyploidy in Spartina[J]. Molecular Ecology, 2005, 14(4): 1163-1175.

[20] Strong D R, Ayres D R. Ecological and evolutionary misadventures of Spartina[J]. Annual Review of Ecology, Evolution, and Systematics, 2012, 44(1): 389-410.

[21] Zhang Z Z, Lin Y, Ma Y J. Effect of trap position on the efficiency of trapping in treelike scale-free networks[J]. Phys. A: Math. Theor. 2011,44(7): 075102.

[22] Redner S. A guide to first-passage processes [J]. American Journal of Physics, 2001, 70(11): 49-70.

[23] Noh J D, Rieger H. Random walks on complex networks[J]. Phys Rev Lett, 2004, 92(11): 118701.

[24] Condamin S, Benichou O, Moreau M. First-passage times for random walks in bounded domains[J]. Phys Rev Lett, 2015, 95(26): 260601.

[25] Lin Y, Julaiti A, Zhang Z Z. Mean first-passage time for random walks in general graphs with a deep trap[J]. J Chem Phys, 2012, 137(12): 124104.

[26] Wu B, Lin Y, Zhang Z Z, et al. Trapping in dendrimers and regular hyperbranched polymers[J]. J Chem Phys, 2012, 137(4): 044903.

[27] Zhang Z Z, Yang Y H, Lin Y. Random walks in modular scale-free networks with multiple traps[J]. Phys Rev E, 2012, 85(1): 011106.

[28] Roy S, Singh J S. Consequences of habitat heterogeneity for availability of nutrients in a dry tropical forest[J]. Journal of Ecology, 1994, 82(3): 503-509.

[29] Bagrow J P.Communities and bottlenecks: trees and treelike networks have high modularity[J]. Physical Review E, 2012, 85(6): 066118.

[30] Benton T G, Vickery J A, Wilson J D. Farmland biodiversity: is habitat heterogeneity the key?[J]. Trends in Ecology & Evolution, 2003, 18(4): 182-188.

[31] Cheng X, Luo Y, Chen J, et al. Short-term C4plant Spartina alterniflora invasions change the soil carbon in C3plant-dominated tidal wetlands on a growing estuarine Island[J]. Soil Biology & Biochemistry， 2006, 38(12): 3380-3386.

[32] Xiao D. Study on spreading patterns and mechanism of an invasive Spartina alterniflora on the saltmarshes in the Yangze Estuary[D]. Shanghai: East China Normal University 2010.

[33] Warren R S, Fell P E, Grimsby J, et al. Rates, patterns, and impacts of Phragmites australis expansion and effects of experimental Phragmites control on vegetation, macroinvertebrates, and fish within tidelands of the lower connecticut river[J]. Estuaries, 2001, 24(1): 90-107.

[34] Wang Q, Wang C, Zhao B, et al. Effects of growing conditions on the growth of and interactions between salt marsh plants: implications for invasibility of habitats[J]. Biological Invasions, 2006,8(7): 1547-1560.

[35] 杜莎， 韩定定， 李德志. 克隆植物的演化博弈研究[J].复杂系统与复杂性科学， 2016,13(1)： 95-101. Du Sha, Han Dingding, Li Dezhi. The evolutionary game study on a clonal plant spartina alterniflora loisel[J]. Complex Systems and Complexity Science, 2016, 13(1): 95-101.

[36] Qian J H, Yang C H, Han D D, et al. Multi-scaling mix and non-universality between population and facility density[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391(21): 5146-5152.

[37] Han D D, Qian J H, Ma Y G. Emergence of double scaling law in complex systems[J]. Europhysics Letters, 2011, 94(2): 28006.

(责任编辑 耿金花)

Random Walk on the Clonal Network of Spartina Alterniflora

YU Yanzea, CHEN Xia, LI Dezhib, HAN Dingdinga

(a.School of the Information Science Technology; b.School of Ecological and Environmental Science,East China Normal University, Shanghai 200241, China)

Trapping process constituted a primary problem of random walks. Based on the field survey data and the theory of complex network, four types of nodes and four types of edges were defined, and then the multiple relationship networks of Spartina alterniflora genets were constructed, which showed disassortativity. In order to explore the topological and dynamic characteristics of the multiple relationship networks ofS. alterniflora genets, the random walk models with multiple traps were established. The simulation result showed that the bunches and the ramets without spikes were the major regulatory nodes of ATT in the random walks. We concluded that the horizontal spatial diffusion network patterns ofS. alterniflora genets revealed by the models reflected their habitat heterogeneity patterns. Furthermore, this type of models might generally provide a reference for the analysis on the heterogeneity patterns of the habitats of other clonal plants.

spartina alterniflora; random walk; trapping node; habitat heterogeneity

1672-3813(2017)02-0082-07；

10.13306/j.1672-3813.2017.02.012

2016-11-01；

2016-12-16

国家自然科学基金(31170387, 31370435, 31570373)

余艳泽(1990-)，男，湖北荆州人，硕士研究生，主要研究方向为复杂网络及其智能化信息处理。

N94

A