基于注资-有界分红的随机微分投资-再保博弈

孙宗岐，刘宣会，陈思源，冀永强，娄建军

1)西安思源学院高数教研室, 陕西西安 710038; 2)西安工程大学理学院, 陕西西安 710048

【数学与应用数学 / Mathematics and Applied Mathematics】

基于注资-有界分红的随机微分投资-再保博弈

孙宗岐1，刘宣会2，陈思源1，冀永强1，娄建军1

1)西安思源学院高数教研室, 陕西西安 710038; 2)西安工程大学理学院, 陕西西安 710048

研究存在模型风险时保险公司的最优投资-再保-注资-有界分红的策略问题．在分红与注资之差的总量现值的期望最大化的准则下，使用随机微分博弈理论建立保险公司的随机微分博弈，通过求解Hamilton-Jacobi-Bellman-Isaacs方程得到最优投资-再保-注资-有界分红策略的显式解，采用数值算例分析验证了本研究所提策略的合理性．

运筹学；对策论；随机微分博弈； Hamilton-Jacobi-Bellman-Isaacs方程；投资策略；比例再保险策略；注资-有界分红；模型风险

随机控制理论是研究投资组合选择的常用方法．1994年随机控制理论首次被运用到保险精算领域， Asmussen等[1-3]运用该理论研究了保险公司的投资、再保险和分红等最优决策问题．然而，这些研究要么在风险模型上改进，要么在状态变量的分布上精益求精．显然任何事先的假设都与真实世界存在差异，这种差异通常被称为模型风险．模型风险和一般所谓的风险之间的区别在于，模型风险随机过程的分布往往是模糊甚至未知的，因此把模型风险刻画为概率测度的不确定性显然是合理的，这就是随机微分博弈的主要思想．

随机微分博弈理论是将随机分析与微分博弈相结合的一门数学理论．1965年，Isaacs[4]首次将数学模型运用到博弈论中．1976年，Elliote[5]建立了随机微分博弈的值函数的存在性和Isaacs条件之间的关系，为随机微分博弈理论在金融数学上的应用打开了理论通道．之后，Taksar等[6]将随机微分博弈引入到保险资金的管理中，研究了非比例再保险问题．Bensoussan[7]等研究了基于非零和随机微分博弈的一系列最优消费和再保险策略．Zeng[8-9]研究了随机微分博弈下的再保险问题．Lin等[10]研究了跳-扩散模型下对一个未知模型的保险最优投资组合问题．罗琰等[11]考虑了模型不确定性因素下基于随机微分博弈的保险公司投资-再保问题．杨鹏等[12-13]分析了随机微分博弈下的保险公司的资产负债管理问题．

以上研究都考虑了模型风险，运用随机微分博弈理论，将经济环境或者再保险公司视为是博弈中虚拟的“对手”，通过建立反映“对手”状态的随机概率测度来度量随机微分博弈参考准则，并在此准则下求解最优博弈策略．然而迄今仍鲜见随机微分博弈理论框架下讨论保险公司最优分红策略的研究．

理论研究人员通常认为分红机制的基本形式有阀值分红和有界分红．然而， Sethi等[14]指出，若单纯按此策略进行红利分配，从理论上讲一定会发生破产．为此，建议在模型中引入注资策略，即一旦公司出现赤字，可通过面向股东或者其他渠道，注入一定的资金以防破产，从而使公司继存下去．Sethi等[14]利用随机控制理论研究了扩散风险模型下最优注资-分红策略问题，其结果具有永久不破产的良好属性．该结论得到了Dickson等[15-16]的认同．近年来，中国学者也开始关注该问题，如张帅琪等[17]研究了带注资的二维复合泊松风险模型的最优分红．王永茂等[18]研究了基于经典风险模型的最优分红和注资策略．然而，这些研究都未考虑到竞争对手市场上不确定性因素对风险过程的影响．

为此，本研究对保险公司注资-有界分红的随机微分投资-再保博弈问题进行探究，将市场视作保险公司无形的竞争对手，考虑保险公司和对手之间的零和随机微分博弈问题．假设保险公司是博弈的主导者，在市场最坏(熊市)的情况下，保险公司选择一个最优的投资-再保险策略，使其分红与注资之差的累积贴现的期望达到最大．

1 建立模型

假设允许连续交易且资产可任意分割，市场不存在摩擦，整个投资过程是自融资的且无套利．

1.1 风险模型的建立及分红机制

模型风险产生的根源在于经济环境的不确定性，所以为刻画这种不确定性，本研究引入参考的完备概率空间(Ω,Ft,F,P)． 其中， ∀ω∈Ω表示直到投资过程的终止时刻T为止的一个完整的经济环境，Ω表示截至T时刻的一个完整的经济环境；Ft(ω)为截至t时刻产生的σ-代数；F(ω)为截至T时刻产生的σ-代数；P为保险公司起初参考的概率测度．

1.1.1 建立参考概率测度下保险公司风险模型

参考概率空间(Ω,Ft,F,P)建立风险模型．保险公司经典的盈余过程为

R(t)=x0+ct-S(t)

(1)

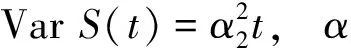
Taksar等[19]认为，经典的盈余过程可近似地用扩散过程来描述，即

(2)

(3)

考虑保险公司可以在破产前将部分盈余投资于其价格为P(t)， 且满足方程

(4)

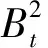
dR(t)= [R(t)r0+π(t,x)(μ0-r0)+

(5)

继续考虑再保险业务，设再保险的自留比例为q(t,x)， 再保险的保费安全负载为η，η>θ， 则盈余过程可描述为

dR(t)= {π(t,x)μ0+[R(t)-π(t,x)]r0+

(1+θ)α1-[1-q(t,x)(1+

(6)

整理后可得

dR(t)= [R(t)r0+π(t,x)(μ0-r0)+

(θ-η)α1+q(t,x)ηα1]dt+

(7)

称满足以下条件的控制策略(π(t,x),q(t,x))的全体构成的集合为可行集Π： ① (π(t,x),q(t,x))是Ft自适应的； ② ∫0Tπ2(t,x)dt<∞ a·e，q(t,x)≤1； ③ (π(t,x),q(t,x))是方程(1)的唯一强解．

1.1.2 自然控制的概率测度刻画

保险公司主观选择的经济环境和市场真实的经济环境之间肯定存在差异，本研究将这种差异刻画化为随机过程θ(t)， 并在此基础上给出自然控制的随机概率测度Pθ．

(8)

显然，Zθ(t)是(Ft,P)上的局部鞅．进一步假设{θ(t):t≥0}是关于概率测度P-a.e有界的，则Zθ(t)是(Ft,P)上的鞅，因此E[Zθ(T)]=E[Zθ(0)]=1．

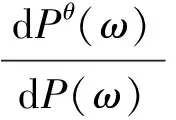
1.1.3 注资-有界分红机制

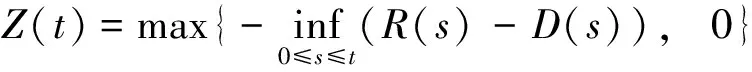
(9)

在注资-分红机制下保险公司的盈余过程为

R(t)D,Z,π,q=R(t)-D(t)+Z(t)

(10)

若策略(D,Z)满足

P(R(t)D, Z, π, q≥0,

(11)

则称其为允许策略，记全体允许策略的集合为H． 以下考虑的注资-分红策(D,Z) ∈H．

1.2 保险公司的随机微分博弈问题

考虑在有限时间段[0,T]内，在保险公司和资本市场之间进行二人-零和随机微分博弈，作为主导者的保险公司，其对手是市场．记值函数为

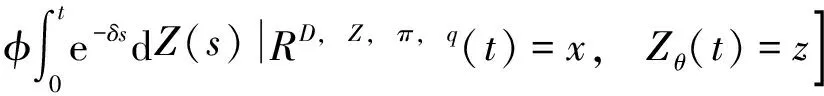
∀t∈[0,T]

(12)

其中，δ为贴现率，δ1为惩罚因子，表示如果发生破产，需注入实际损失的φ倍资金作为惩罚．

保险公司的目标是通过选择最优的投资策略π*(t,x)和再保策略q*(t,x)， 使在市场最坏情形下的值函数最大，而市场的目标是通过选择最坏的环境θ*(t)使值函数最小，即最优值函数为

Jπ*, q*, θ*(t,x,z;b)

(13)

s.t. dR(t)= [R(t)r0+π(t,x)(μ0-r0)+

(θ-η)α1+q(t,x)ηα1]dt+

(14)

其中，J(t,x,z;b)为分红与注资之差的总现值的期望；Jπ*, q*, θ*(t,x,z;b)为最大分红注资之差的总现值期望．

式(13)和式(14)即本研究提出的随机微分博弈问题．

2 随机微分博弈问题的求解

2.1Hamilton-Jacobi-Bellman-Isaacs(HJBI)方程

设函数f(t,x,z) ∈C1,2,2(R3)， 本研究定义无穷小微分算子为

Λπ,q,θf=ft+[xr0+π(t,x)(μ0-r0)+

(θ-η)α1+q(t,x)ηα1]fx+

zθ(t)(q(t,x)α2+π(t,x)σ0)fxz+

z2θ2(t,x)fzz-δf

(15)

其中，f为f(t,x,z)；ft为f(t,x,z)关于t的导数；fx为f(t,x,z)关于x的导数；fxx为f(t,x,z)关于x的二阶导数；fzz为f(t,x,z)关于z的二阶导数；δ为贴现率常数．

于是，得到紧凑形式HJBI方程为

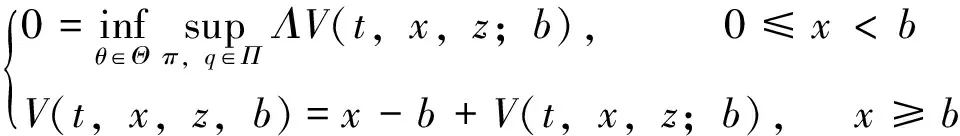
(16)

2.2 最优投资-再保策略和最优值函数的求解

记所有满足以下条件的控制策略(π(t,x),q(t,x))的集合为可行集Π．

HJBI方程具有如下形式

1) 当0≤x

π(t)σ0]Vxz+z2θ2(t)Vzz-δV}

(17)

其中，V为值函数；Vt为V关于t的一阶导数；Vx为V关于x的一阶导数；Vxx为V关于x的二阶导数;Vxz为V关于x再关于z的二阶偏导．

2) 当x≥b时，有

V(t,x,z;b)=x-b+V(t,b,z;b)

(18)

其中，V(t,x,z;b)为最优值函数；b为分红边界；V(t,b,z;b)为修正盈余为b时的最优值函数的值．其边界条件为Vx(T, 0, 1;b)=φ和Vx(T,b, 1;b)=1.

2.2.1 当0≤x

考虑到要满足引理中的各个条件，以及文献[21]的结果，猜测值函数需具有以下形式

V(t,x,z;b)=g(t)z×

(19)

其中， 0≤x

Vzz=0

将V(t,x,z;b)的各阶导数代入方程(17)，可得

(20)

其中，g(t)为时间函数；g′(t)为g(t)的一阶导数；h(t)为另一时间函数；h′(t)为h(t)的一阶导数；k为常数；σ0为风险资产收益的波动率．

由一阶最优性条件可得

(21)

(22)

将式(21)和式(22)代入方程(20)，可得

(23)

对方程(23),由一阶最优性条件可得

(24)

将式(24)代入方程(20)，可得

(25)

于是得到常微分方程

(26)

(27)

g(T)=1

(28)

h(T)=0

(29)

因此可解得

(30)

(31)

最后，将式(24)代入式(21)和(22)，可得

(32)

(33)

由式(25)、式(30)和式(31)可得，当t=T时，有

(34)

整理后有

δ=0

(35)

显然

4r0δ>0

(36)

则

(37)

此时，可验证Vx(T,b, 1;b)=1成立．

由边界条件(6)中Vx(T, 0, 1;b)=φ可得

(38)

2.2.2 当x≥b时的最优投资-再保博弈策略和最优值函数

当x≥b时，最优投资-再保险策略和最优市场策略与0≤x

V(t,x,z;b)=x-b+g(t)z×

(39)

综上可见，当保险公司选择的经济环境与市场真实的经济环境吻合，即θ(t)=0时，g(T)=1和h(T)=0， 此时最优投资-再保策略的解析表达与文献[21]中不考虑模型风险时的结果一致，因此，文献[21]的结果可视为本研究结果的特殊情形．

3 数值算例及结果分析

通过算例分析存在模型风险时财富x对最优投资-再保策略的影响．

当θ(t)=0时，方程(17)和方程(18)就是一般的最优控制问题，此时根据式(21)和式(22)可得到在保险公司初始选择的概率测度就是自然控制的概率测度时，最优控制策略为

(40)

(41)

算例 设m=0.5，λ=1，θ=0.3，η=0.5，μ0=0.1，σ0=0.1，b=1，r0=0.025． 利用Matlab软件可得如图1的最优投资策略π*(x)的图像，以及如图2的最优比例再保险策略1-q*(x)的图像．

图1 最优投资策略π*(x)与财富x之间的函数关系Fig.1 Function relation between the optimal investment strategy π*(x) and wealth x

图2 最优再保策略1-q*(x)与财富x之间函数关系Fig.2 Function relation between the optimal reinsurance strategy 1-q*(x) and wealth x

从图1可见，最优投资策略π*(x)是财富x的减函数，这是因为保险公司的财富越多，赔付能力就越强，在盈余充足的保证下，为降低整体的风险水平，会减少风险投资；由图1还可见，在恶劣市场环境下，保险公司在风险资本上的投资要比良好市场时低，这是因为在恶劣经济环境下，保险公司面临的风险水平很高，为降低风险水平，会持保守态度，减少其风险资本投资．

从图2可见,当保险公司选择的概率测度与自然控制的概率测度一致，即市场良好时，公司盈余充足，此时为降低整体风险水平，最优投资策略π*(x)应随财富x的增大而减小，最优再保险策略1-q*(x)随财富x的增大而增大；而在恶劣市场环境下，最优再保策略大于1，说明此时保险公司不仅会将全部投保风险转嫁给再保险公司，而且会为部分风险资本购买保险(如跌停险)，以达到转移风险，降低保险公司整体风险水平的目的．同时也可看出，随着财富x的增加，再保险策略会逐渐减小，这是因为公司盈余逐渐充足，公司赔付能力渐增，自然也会渐减再保险的比例．

结 语

通过分析具有模型风险的保险公司最优投资-比例再保策略和最大注资-有界分红问题发现，保险公司在恶劣市场下，应持有保守态度，即减少风险投资增加再保险比例；随着保险公司财富的增加，抗风险能力得到提高，此时不论是恶劣市场下，还是良好市场下，为降低整体风险水平，风险投资都应随着公司财富的增加而减小；对于再保险比例而言，在恶劣市场情形下，保险公司的盈余增加，抗风险能力提高，再保险比例应降低，但在良好市场情形下，公司盈余充足，财富虽然增加，但是风险投资减少，再保险比例增加，方能达到财富充足时降低整体风险水平的目的．在保险资金的实际管理中，阀值分红和线性有界分红也是保险公司常常考虑的分红机制，此外，除了比例再保险策略，超额损失再保险同样也是保险公司常用的再保险策略，因此，研究阀值分红和线性有界分红机制下的保险公司注资-分红准则的随机微分投资-再保策略问题将是下一步研究的重点．

/ References：

[1] Asmussen S, Tacksar M. Controlled diffusion models for optimal dividend pay-out[J]. Insurance: Mathematics and Economics, 1997, 20(1): 1-15.

[2] Hojgaard B. Optimal dividend pay-out with the option of proportional reinsurance in the diffusion model[J]. Insuranse: Mathematics and Economics, 1997, 20(2): 151.

[3] Schmidli H. Optimal proportional reinsurance policies in a dynamic setting[J]. Scandinavian Actuarial Journal, 2001, 2001(1): 55-68.

[4] Isaacs R. Differential games[M]. New York: Wiley, 1965．

[5] Elliote R. The existence of value in stochastic differential games[J]. SIAM Journal on Control and Optimization, 1976, 14(1): 85-94.

[6] Taksar M，Zeng Xudong. Optimal nonproportional reinsurance control and stochastic differential games[J]．Insurance：Mathematics and Economics, 2011, 48(1)：64-71．

[7] Bensoussan A, Siu C C, Yam S C P, et al. A class of non-zero-sum stochastic differential investment and reinsurance games[J]. Automatica, 2014, 50(8): 2025-2037.

[8] Zeng Xudong. Optimal reinsurance with a rescuing procedure[J]. Insurance: Mathematics and Economics, 2010, 46(2): 397-405．

[9] Zeng Xudong．A stochastic differential reinsurance games[J]. Journal of Applied Probability, 2010, 47(2): 335-349．

[10] Lin Xiang, Zhang Chunhong, Siu T K. Stochastic differential portfolios games for an insurer in a jump-diffusion risk process[J]. Mathematics Method of Operations Research, 2012, 75(1): 83-100.

[11] 罗 琰，杨招军．基于随机微分博弈的保险公司最优决策模型[J]．保险研究，2011，8(20)：48-52． Luo Yan, Yang Zhaojun. Optimal strategy of insurer based on stochastic differential[J]. Insurance Studies, 2010, 8(20):48-52.(in Chinese)

[12] 杨 鹏，林 祥．随机微分博弈下的资产负债管理[J]．中山大学学报自然科学版，2013，52(6)：30-34． Yang Peng, Lin Xiang. Asset and liability management under stochastic differential games[J]. Acta Scientiarum Naturalium Universitaties Sunyetseni, 2013, 52(6): 30-33.(in Chinese)

[13] 杨 鹏．基于再保险和投资的随机微分博弈[J]．数学杂志，2014，34(4)：779-786． Yang Peng. Stochastic differential games with reinsurance and investment[J]. Journal of Mathematics, 2014, 34(2): 779-786.(in Chinese)

[14] Sethis S P, Taksar M I．Optimal financing of a corporation subject to random returns[J]. Mathematical Finance, 2002,1(12): 155-172.

[15] Dickson D C M, Waters H R. Some optimal dividend problems[J]. ASTIN Bulletin: the Journal of the International Actuarial Association, 2004, 34(1): 49-74.

[16] Gerber H U, Shiu E S W. On optimal dividend strategies in the compound Poisson model[J]. North American Actuarial Journal, 2006, 10(2): 76-93.

[17] 张帅琪，刘国欣．带注资的二维复合泊松模型的最优分红[J].运筹学学报,2012,16(3)：119-131. Zhang Shuaiqi, Liu Guoxin. Optimal dividend payments of the two-dimensional compound Poisson risk model with capital injection[J]. Operations Research Transactions, 2012, 16(3): 119-131.(in Chinese)

[18] 王永茂，祁晓玉，贠小青．基于经典风险模型的最优分红和最优注资策略研究[J]．郑州大学学报理学版，2015，47(2)：37-40． Wang Yongmao, Qi Xiaoyu, Yun Xiaoqing. Optimal dividend capital injection strategy in classical risk model[J]. Journal of Zhengzhou University Natural Science Edition, 2015, 47(2): 37-40.(in Chinese)

[19] Taksar M I, Markussen C. Optimal dynamic reinsurance policies for large insurance portfolios[J]. Finance and Stochastics, 2003, 7(1): 97-121.

[20] Mataramvura S, ∅ksendal B. Risk minimizing portfolios and HJBI equations for stochastic differential games[J]. Stochastics: an International Journal of Probability and Stochastic Processes, 2008, 80(4): 317-337.

[21] 孙宗岐，刘宣会，陈思源，等．动态VaR约束下带有界分红的最优再保策略[J]．云南民族大学学报自然科学版，2016，25(5)：463-468． Sun Zongqi, Liu Xuanhui, Chen Siyuan, Ji Yongqiang. Optimal reinsurance approach with barrier dividend under dynamic VaR constraint[J]. Journal of Yunnan University of Nationalities Natural Sciences Edition, 2016, 25(5): 463-468.(in Chinese)

【中文责编：英 子；英文责编：木 南】

2016-10-21；Accepted：2017-01-20

Assocoate professor Liu Xuanhui. E-mail: lxhlll2011@163.com

Stochastic differential investment-reinsurance games with capital injection-barrier dividend

Sun Zongqi1, Liu Xuanhui2, Chen Siyuan1, Ji Yongqiang1, and Lou Jianjun1

1) Department of Mathematics, Xi’an Siyuan University, Xi’an 710038, Shaanxi Province, P.R.China 2) College of Science, Xi’ an Polytechnic University, Xi’an 710048, Shaanxi Province, P.R.China

To better reflect the insurance practice and help insurance company make more robust strategy, we investigate the optimal investment-reinsurance-capital injection-barrier dividend problem when model risk exists. Based on the criterion of maximizing the expected total present value of the difference between barrier dividend and capital injection, the stochastic differential game model is utilized based on stochastic differential game principle, and the optimal policy is obtained by solving the Hamilton-Jacobi-Bellman-Isaacs (HJBI) equation. The closed-form optimal investment-reinsurance-capital injection-barrier dividend strategies are derived. The economic analyses illustrate the reasonableness of the obtained theoretical results.

operations research; game theory; stochastic differential game; Hamilton-Jacobi-Bellman-Isaacs equation; investment strategies; proportional reinsurance; capital injection-barrier dividend; model risk

：Sun Zongqi, Liu Xuanhui, Chen Siyuan, et al. Stochastic differential investment-reinsurance games with capital injection-barrier dividend[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(4): 364-371.(in Chinese)

O 211.63

A

10.3724/SP.J.1249.2017.04364

国家自然科学基金资助项目(71371152)；陕西省教育厅自然科学专项基金资助项目(2016JK2150)；西安思源学院2016年度科研基金资助项目(XASY-B1617)

孙宗岐(1979—)，男，西安思源学院讲师．研究方向：随机分析与随机运筹．E-mail:szqi200679@sina.com

Foundation：National Natural Science Foundation of China (71371152); Natural Science Foundation of the Education Department of Shaanxi Province (2016JK2150 ); Xi’an Siyuan University Research Fund 2016 Annual (XASY-B1617)

引 文：孙宗岐，刘宣会，陈思源，等．基于注资-有界分红的保险公司随机微分投资-再保博弈[J]. 深圳大学学报理工版，2017，34(4)：364-371.