有界线性算子的a-Weyl定理及亚循环性
2017-07-18杨国增孔莹莹曹小红
杨国增,孔莹莹,曹小红
1)郑州师范学院数学与统计学院,河南郑州 450044;2)陕西师范大学数学与信息科学学院,陕西西安710062

【数学与应用数学 / Mathematics and Applied Mathematics】
有界线性算子的a-Weyl定理及亚循环性
杨国增1,孔莹莹2,曹小红2
1)郑州师范学院数学与统计学院,河南郑州 450044;2)陕西师范大学数学与信息科学学院,陕西西安710062
线性算子理论;a-Weyl定理;逼近点谱;亚循环算子;算子函数;Fredholm算子;谱集;Browder谱
设H为无限维复可分的Hilbert空间,B(H)为H上的有界线性算子的全体.对于T∈B(H), 令N(T)和R(T)分别表示算子T的零空间和值域,若R(T)闭且n(T)=dimN(T)有限,称T为上半Fredholm算子;若R(T)有有限的余维数d(T)=dim(H/R(T))=codimR(T), 则称T∈B(H)为下半Fredholm算子.若T既为上半Fredholm算子又为下半Fredholm算子,则T∈B(H)称为Fredholm算子.对于半Fredholm算子,其指标定义为ind(T)=n(T)-d(T). 其中,n(T)和d(T)分别为算子T的零空间维数和值域的余维数.特殊地,当n(T)=0且R(T)闭时,称T为下有界算子.指标为0的Fredholm算子称为Weyl算子.算子T的升标asc(T)为满足N(Tn)=N(Tn+1)的最小非负整数,若这样的整数不存在,则记asc(T)=∞; 算子T的降标为满足R(Tn)=R(Tn+1)的最小的非负整数,同样若这样的整数不存在,则记des(T)=∞. 当T为有限升标和有限降标的Fredholm算子时,称T为Browder算子.
对T∈B(H),记σ(T),σw(T),σp(T),σa(T),σb(T),σab(T)、σSF(T)和σea(T)分别表示算子T的谱、Weyl谱、点谱、逼近点谱、Browder谱、Browder本质逼近点谱、半Fredholm谱和本质逼近点谱.记ρ(T)=Cσ(T)、ρa(T)=Cσa(T)、ρb(T)=Cσb(T)、ρab(T)=Cσab(T)、ρSF(T)=CσSF(T)、ρea(T)=Cσea(T). 令Pab(T)={λ∈σa(T):T-λI为上半Fredholm算子,且asc(T-λI)<∞}, 将T的正规特征值记作σ0(T), 即σ0(T)=σ(T)σb(T). 对K⊆C, isoK表示集合K的孤立点集, accK为K的聚点的全体;为单位圆盘;为单位圆周.



设H(T)为在σ(T)的一个邻域上解析,但在σ(T)的任一个分支上不为常值的函数全体.本研究用谱集σvaw(T)刻画了对任意f∈H(T),f(T)满足a-Weyl定理的判定方法,进而给出当T为亚循环算子时,f(T)满足a-Weyl定理的充要条件.
1 预备知识
令T∈B(H), 若σ为σ(T)中的一闭开子集,则存在一个解析的柯西邻域Ω满足σ⊆Ω, 且

(1)

(2)
按Ω的正向积分,又令H(σ;T)=R(E(σ;T)). 显然,若λ∈isoσ(T), 则{λ}为σ(T)中的闭开子集,记H({λ};T)为H(λ;T); 除此之外,若dimH(λ;T)<∞, 则λ∈σ0(T)[11].
为便于证明,本研究首先给出引理1至引理3.
引理1[12]设T∈B(H), 若σ(T)=σ1∪σ2, 其中,σ1和σ2为σ(T)中的闭开子集且σ1∩σ2=∅, 则
(3)
且T的分解为
(4)
其中,σ(Ti)=σi(i=1, 2).
引理2[13]设T∈B(H), 若asc(T)≤p(p为某个非负整数),则N(Tk)∩R(Tp)={0}. 其中,k=1, 2, ….
引理3[14]设T∈B(H), 若λ∈isoσ(T),则下列叙述是等价的:①λ∈ρSF(T); ②λ∈ρw(T); ③λ∈σ0(T).
2 定理与证明
定理1 设T∈B(H), 则下列叙述是等价的:
1)σ(T)=σa(T)且T满足a-Weyl定理;
2)ρvaw(T)={λ∈isoσ(T)∶n(T-λI)=0}∪σ0(T)∪ρ(T);
3)σ(T)=σvaw(T)∪{λ∈isoσ(T)∶n(T-λI)=0}∪σ0(T).
【证】首先证明 1)⟹2).这只需证明
ρvaw(T)= {λ∈isoσ(T)∶n(T-λI)=
0}∪σ0(T)∪ρ(T)
(5)
假设λ∈ρvaw(T)且λ∉ρ(T), 则根据引理2,n(T-λI)<∞且λ∈isoσa(T)∪ρa(T), 由于σ(T)=σa(T), 则有λ∈isoσ(T). 若n(T-λI) =0, 则λ∈{λ∈isoσ(T)∶n(T-λI)=0}; 若0 其次,证明 2)⟹1).若T-λI为下有界算子,则λ∈ρvaw(T). 当λ∈{λ∈isoσ(T)∶n(T-λI)=0}, 根据引理3,λ∈ρ(T), 这与λ∈isoσ(T)矛盾;而当λ∈σ0(T),λ∈ρ(T), 同样得到与λ∈σ0(T)矛盾.于是σ(T)=σa(T). 最后证明 2)⟺3).对2)中的等式变形,可得该式等价于 C=σvaw(T)∪{λ∈isoσ(T)∶n(T-λI)= 0}∪σ0(T)∪ρ(T) (6) 上式等价于σ(T)=σvaw(T)∪{λ∈isoσ(T)∶n(T-λI)=0}∪σ0(T). 注解1 1) 在定理1中,σ(T)=σa(T)是本质的.例如,设T∈B(l2)定义为T(x1,x2, …)=(0,x1,x2, …), 则有σ(T)=,σa(T)=σea(T)=,∅, 以及ρvaw(T)={λ∈C于是可得σ(T)≠σa(T),T满足a-Weyl定理,但因 {λ∈isoσ(T):n(T-λI)=0}∪σ0(T)∪ (7) 则有 ρvaw(T)≠ {λ∈isoσ(T)∶n(T-λI)= 0}∪σ0(T)∪ρ(T) (8) 推论1 当且仅当σ(T)∈{λ∈isoσ(T):n(T-λI)=0}∪σ0(T)时,σvaw(T)=∅,σ(T)=σa(T)且T满足a-Weyl定理. 注解2 1) 在推论1中, 当σvaw(T)=∅,σ(T)=σa(T)且T满足a-Weyl定理时,σ(T)为有限集. 推论2 当且仅当σ(T)为有限集且σp(T)=σ0(T)时,σvaw(T)=∅,σ(T)=σa(T)且T满足a-Weyl定理. 下面给出算子函数满足a-Weyl定理的判断方法. 定理2 若σ(T)=σa(T),则对任意的f∈H(T),f(T)满足a-Weyl定理当且仅当下列条件成立: 1) 对任意给定f∈H(T), 有f(σvaw(T))⊆σvaw(f(T)); 2)T满足a-Weyl定理; 3)σa(T)=σea(T)或ρvaw(T)=ρa(T)∪Pab(T). 【证】 必要性. 由于f(T)满足a-Weyl定理,根据引理2,则μ0∈isoσa(f(T))∪ρa(f(T)). 设f(T)-μ0I=(T-λ1I)n1(T-λ2I)n2…(T-λkI)nkg(T), 其中,λi≠λj(i≠j, 1≤i,j≤k),g(T)可逆. 若μ0∈ρa(f(T)), 则λi∈ρa(T),λi∈ρvaw(T), 故μ0∉f(σvaw(T)); 若μ0∈isoσa(f(T)), 则λi∈isoσa(T)∪ρa(T). 又因n(T-λiI) 条件 2)显然成立. 条件 3)分两种情况讨论. 令σ1={λ1},σ2={λ2}, 则σ1和σ2为σ(T)中的闭开子集,根据引理1,T有分解 其中,σ(T1)={λ1};σ(T2)={λ2};σ(T3)=σ(T){λ1,λ2};M为H(λ1;T1)与H(λ2;T2)的正交补空间. 令f(T)=(T-λ1I)(T-λ2I), 由于 充分性. 事实上,设f(T)-μ0I为上半Fredholm算子且ind (f(T)-μ0I)≤0, 并设f(T)-μ0I=(T-λ1I)n1(T-λ2I)n2…(T-λkI)nkg(T), 其中,λi≠λj(i≠j, 1≤i,j≤k),g(T)可逆. 由μ0∉σvaw(f(T))可知 λi∈ρvaw(T)=ρa(T)∪{λ∈isoσa(T): n(T-λI)=0}∪Pab(T) (9) 综上可知,对任意给定的f∈H(T),f(T)满足a-Weyl定理. 下面研究算子的亚循环性与a-Weyl定理的关系. 注解3 例如,设T∈B(l2)定义为T(x1,x2, …)=(0,x1,x2, …), 通过计算可得σ(T)=σw(T)=,σa(T)=σea(T)=,∅,σ0(T)=∅,σvaw(T)=. 于是有但T满足a-Weyl定理. 定理3 设T∈B(H), 则下列叙述等价. 3)σ(T)=σvaw(T)∪{λ∈isoσ(T):n(T-λI)=0},且σw(T)∪∂连通; 4)σ(T)=σvaw(T)∪{λ∈isoσ(T):n(T-λI)=0}, 且σ(T)∪∂连通; 5)ρvaw(T)=ρ(T)∪{λ∈isoσ(T):n(T-λI)=0}, 且σw(T)∪∂连通. 【证】2)⟺ 3). 由于σ0(T)=σ0(T)∩σ(T), 而σ0(T)∩σvaw(T)=∅,σ0(T)∩{λ∈isoσ(T):n(T-λI)=0}=∅,于是有σ0(T)=σ0(T)∩σ(T) =∅. 又由于ρSF(T)∩σ(T)=[ρSF(T)∩σvaw(T)]∪[ρSF(T)∩{λ∈isoσ(T):n(T-λI)=0}], 而[ρSF(T)∩{λ∈isoσ(T):n(T-λI)=0}]=∅, 于是有ρSF(T)∩σ(T)=[ρSF(T)∩σvaw(T)]. 1)⟹ 2),显然成立. (10) (11) 同理可知,λi∈isoσ(T)∪ρ(T), 其中2≤i≤m. 显然,n(T-λiI)≤n(f(T)-μ0I)<∞. 因此λ0∉isoσvaw(T), 1≤i≤m. 于是有任给f∈H(T),f(σvaw(T)) ⊆σvaw(f(T)). 根据定理2,任给f∈H(T),f(T)满足a-Weyl定理. 3)⟺ 4).因为σ(T)=σvaw(T)∪{λ∈isoσ(T):n(T-λI)=0} 而σw(T)∩σvaw(T)=σvaw(T),σw(T)∩{λ∈isoσ(T):n(T-λI)=0}={λ∈isoσ(T):n(T-λI)=0},则σw(T)=σw(T)∩σ(T)=σ(T), 故结论成立. 4)⟺ 5)显然成立. 推论3 下列叙述是等价的. 3)σ(T)={λ∈isoσ(T):n(T-λI)=0}且σw(T)∪∂连通. 推论4 下列叙述是等价的. 3)σ(T)为有限集,σp(T)=∅且σw(T)∪∂连通. 因此可证明,在推论4中,“σw(T)∪∂连通”可改为“σ(T)∪∂连通”. 本研究基于新定义的谱集σvaw(T), 给出了对任意的f∈H(T),f(T)满足a-Weyl定理的判定方法,进而研究了当T为亚循环算子时,f(T)满足a-Weyl定理的充要条件.下一步,我们将对一般的算子T的函数演算满足Weyl’s定理进行刻画. / References: [1] Herrero D A. Limits of hypercyclic and supercyclic operators[J]. Journal of Functional Analysis, 1991, 99(1): 179-190. [2] Weyl H. Überbeschränkte quadratische formen, deren differenz vollstetig ist[J]. Rendiconti del Circolo Matematico di Palermo, 1909, 27(1): 373-392. [3] Coburn L A. Weyl’s theorem for nonnormal operators[J]. Michigan Mathematical Journal, 1966, 13(3): 285-288. [4] Berberian S K. An extension of Weyl’s theorem to a class of not necessarily normal operators[J]. Michigan Mathematical Journal, 1969, 16(3): 273-279. [5] Cao Xiaohong, Guo Maozheng, Meng Bin. Drazin spectrum and Weyl’s, theorem for operator matrices[J]. Journal of Mathematical Research and Exposition, 2006, 26(3): 52-66. [6] 青 梅.无界算子的矩阵的谱和补问题[D].呼和浩特:内蒙古大学,2016. Qing Mei. Spectra and completion problems of unbounded operator matrices[D]. Hohhot: Inner Mongolia University, 2016.(in Chinese) [7] Kitson D, Harte R, Hernández C. Weyl’s theorem and tensor products: a counterexample[J]. Journal of Mathematical Analysis and Applications, 2011, 378(1): 128-132. [8] 戴 磊.Weyl型定理的判定及其稳定性[D].西安:陕西师范大学,2013. Dai Lei. The judgment and the stability of Weyl type theorems[D]. Xi’an: Shaanxi Normal University.(in Chinese) [9] 李娜娜.算子与其共轭的Weyl型定理的等价性判定[D].西安:陕西师范大学,2013. Li Nana. The equivalence of Weyl’s theorem of operators and their conjugate[D]. Xi’an: Shaanxi Normal University.(in Chinese) [10] Kato T. Perturbation theory for linear operators[M]. Berlin: Springer-Verlag Berlin Heidelberg, 1976: 11-12. [11] Dunford N, Schwartz J T. Linear operators: part 1 general theory[M]. Berlin: Springer-Verlag Berlin Heidelberg, 1988: 5-6. [12] H Radjavi, P Rosenthal. Invariant subspaces[M]. 2nd edit. New York, USA: Dover Publications, 2003: 63-64. [13] Taylor A E. Theorems on ascent, descent, nullity and defect of linear operators[J]. Mathematische Annalen, 1966, 163(1): 18-49. [14] Conway J B. A course in functional analysis[M]. 2nd edit. New York: Springer-Verlag, 2003: 181-182. [15] Hassane Zguitti. A note on drazin invertibility for upper triangular block operators[J]. Mediterranean Journal of Mathematics, 2013, 10(3): 93-102. [16] 戴 磊,曹小红. 单值延拓性质与广义(ω)性质[J]. 陕西师范大学学报自然科学版,2011,39(2):32-41.DaiLei,CaoXiaohong.Thesinglevaluedextensionpropertyandgeneralizedproperty(ω)[J].JournalofShaanxiNormalUnviersityNaturalScienceEdition, 2011, 39(2): 32-41.(inChinese) [17] 周婷婷.Weyl型定理及相关问题[D].长春:吉林大学,2014.ZhouTingting.Weyl’stheoremandrelatedproblems[D].Changchun:JournalofJilinUniversity, 2014.(inChinese) [18]SunChenhui,CaoXiaohong,DaiLei.AWeyl-typetheoremandperturbations[J].ActaMathtmaticaSinica, 2009, 52(1): 73-80. 【中文责编:英 子;英文责编:木 南】 2016-12-22;Accepted:2017-04-18 Professor Cao Xiaohong. E-mail: xiaohongcao@snnu.edu.cn A-Weyl’s theorem and hypercyclic property for bounded linear operators Yang Guozeng1, Kong Yingying2, and Cao Xiaohong2 1)School of Mathematics and Statistics, Zhengzhou Normal University, Zhengzhou 450044, Henan Province, P.R.China; 2) Shaanxi Normal University, Institute of Mathematics and Information Science, Xi’an 710062, Shaanxi Province, P.R.China linear operator theory; a-Weyl’s theorem; approximate point spectrum; hypercyclic operators; operator function; Fredholm operator; spectrum set; Browder spectrum :Yang Guozeng, Kong Yingying, Cao Xiaohong. A-Weyl’s theorem and hypercyclic property for bounded linear operators[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(4): 372-377.(in Chinese) O A 10.3724/SP.J.1249.2017.04372 国家自然科学基金资助项目(11471200) 杨国增(1980—),男,郑州师范学院讲师.研究方向:泛函算子理论.E-mail:ygz_0907@163.com Foundation:National Natural Science Foundation of China (11471200) 引 文:杨国增,孔莹莹,曹小红.有界线性算子的a-Weyl定理及亚循环性[J]. 深圳大学学报理工版,2017,34(4):372-377.
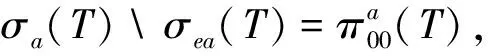

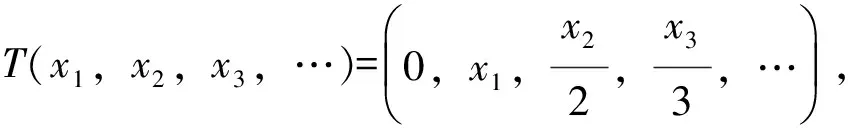






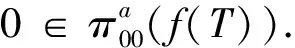







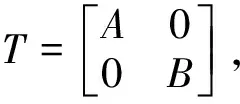




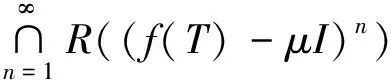







结 语