基于紧密排列土柱模型的冻土热参数计算

陈之祥, 李顺群, 夏锦红, 王 凯, 桂 超

1)天津城建大学土木工程学院，天津 300384；2)天津市软土特性与工程环境重点实验室，天津 300384；3)新乡学院土木工程与建筑学院，河南新乡 453003

【土木建筑工程 / Architecture and Civil Engineering】

基于紧密排列土柱模型的冻土热参数计算

陈之祥1,2, 李顺群1,2, 夏锦红3, 王 凯1,2, 桂 超3

1)天津城建大学土木工程学院，天津 300384；2)天津市软土特性与工程环境重点实验室，天津 300384；3)新乡学院土木工程与建筑学院，河南新乡 453003

为评估热参数对饱和冻土瞬态温度场的影响，分析冻土温度场的影响因素，提出一种最紧密排列的土柱几何模型，土柱外部被自由水充满．假定冻结在土柱围合区域的中心产生并呈柱状发展，根据任意时刻单元体内部土、水和冰的体积构成，依据Johansen的预估土体导热系数计算方法，建立未冻水含量与导热系数之间的计算关系．依据比热加权计算的原理，结合土体的相对密度及水和冰的密度，获取了土柱模型在不同冻结时刻各相的质量比，确定了未冻水含量与比热之间的计算关系．依据不同冻结时刻土柱模型中的未冻水含量，建立潜热随冻结时刻的变化关系．根据实测粉质黏土的导热系数，结合土柱模型获取其比热、潜热随温度的变化关系．将获取的不同温度下的导热系数、比热和潜热值代入数值计算软件ABAQUS，获取了冻土温度场的计算值．将该计算值与实测值进行对比，表明基于该模型获取的计算热参数值能够较好地预测冻土温度场．

岩土工程；冻土；热参数；土柱模型；温度场；未冻水；潜热

冻土的热参数是研究冻土物理学的基础指标，是岩土工程热工计算的重要依据[1]. 土的热参数包括以比热为主的热力学性质及以导热系数为主的迁移性质[1-5]. 在寒冷地区建筑及人工冻结法施工过程中，只有掌握岩土材料的导热系数及比热，才能准确预测工程的温度场，从而进行冻融稳定性分析及隔热层设计[5-9].

受土体矿物成分影响，土中孔隙水的结冰发生在0 ℃以下某个温度区间而不是0 ℃点[10]. 相应的水冰相变释放潜热的过程也发生在这个区间. 另外，液态水的比热和导热系数分别约为固态冰比热和导热系数的2倍和1/4[11]. 因此，土体的比热和导热系数等热参数是随温度变化而变化的.

冻土的热参数主要依据试验和经验公式确定，对于土体特别是冻土尚无通用的热传导模型[12-14]. 研究表明，冻土中的未冻水含量与冻结温度保持着动态平衡的关系[15]，因此，未冻水与导热系数、比热、潜热之间必然存在一定的数学关系.

本研究基于饱和冻土的三相组成和热参数的量纲定义，提出一种最紧密排列的等效土柱几何模型，土柱外部被自由水充满. 假定冻结在土柱围合区域的中心产生并呈柱状发展，根据任意时刻单元体内部土、水、冰的体积构成，依据Johansen[16]的预估土体导热系数计算方法，建立了未冻水含量与导热系数之间的计算关系. 依据比热加权计算的原理，结合土的相对密度和水、冰的密度，获取土柱模型在不同冻结时刻各相的质量比，进而确定未冻水含量与比热之间的计算关系. 依据不同冻结时刻土柱模型中的未冻水含量，建立潜热随冻结时刻变化的关系. 依据实测粉质黏土的导热系数，结合土柱模型获取其比热、潜热随温度的变化关系. 将其随不同温度变化的导热系数、比热、潜热值代入数值计算软件ABAQUS，获得了冻土温度场的计算值，将该温度场计算值与实测值进行了对比.

1 冻土热参数计算模型

本研究类比冻土的三相构成和热参数的量纲定义，建立了基于最紧密排列土柱的等效热参数模型. 通过计算不同时刻等效模型中土柱、冰柱和孔隙水的比例关系，建立未冻水含量与热参数之间的计算关系，确立了导热系数、比热和潜热之间的数值关系.

1.1 土柱热传导模型

热参数模型由管径相同的土柱依据最紧密排列的形式叠合而成，土柱外被孔隙水充满，如图1. 在土体表面能的作用下，土中水分为不同的结合能量级别，冻土中的未冻水最大程度上存在于靠近土体的区域[17-19]. 基于此，假定冻结在3个土柱围合成的孔隙水单元中心产生，并呈柱状发展直至孔隙水冻实.

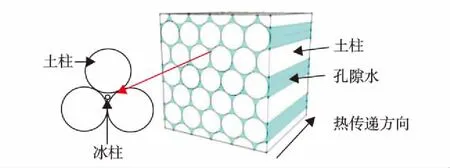
图1 土柱热传导模型Fig.1 (Color online) The soil column model of heat conduction

1.2 模型计算

将土柱等效模型的冻结分为初始冻结阶段和接触阶段. 在初始冻结阶段，冰柱与土柱呈相离状态；随着冻结的深入，冰柱与土柱相切和相交，即为接触阶段. 按照初始冻结和接触阶段进行冻土中不同时刻各相含量的计算.

设冻结冰柱半径为r， 土柱半径为R. 如图1，取1m3进行冻土中各相比例的确定，取立方体截面中心为某土柱截面的圆心，依次排列土柱从而进行计算数量的确定.

3个土柱围成的封闭区域截面面积为

(1)

单元体内完整封闭区域个数为

(2)

单元体中完整封闭区域内自由水体积为为

(3)

单元体积内土柱所占体积为

Vs=1×109-Vf

(4)

若冻结柱体积为Vi， 则此刻土体单元中的未冻水理论体积为

Vw=Vf-Vi

(5)

在初始冻结阶段，

(6)

在接触阶段，

(7)

其中，

(8)

r应满足

(9)

1.3 热参数计算

根据任意冻结时刻等效土柱模型中土柱、孔隙水、冰柱之间的体积比，依据Johansen的预估土体导热系数计算方法，可获取不同冻结时刻土体的导热系数. 依据任意冻结时刻土体中土柱、孔隙水、冰柱之间的质量比，按照比热加权平均计算的思想，可获取不同冻结时刻土体的比热.

1.3.1 计算比例确定.

考虑土中水相变成冰后的体积增量[12]，单位模型中土柱、孔隙水、冰柱的体积比rj和质量比mj分别为

(10)

(11)

其中，rj和mj分别表示单位体积中j相所占的体积比和质量比；Vj表示单位体积中j相所占的体积；ρj为j相的密度；ds为土的相对密度；ρf和ρi分别为水和冰的密度.

1.3.2 热参数确定.

根据Johansen[16]的广义几何平均法估算土体的导热系数为

(12)

其中，λi、λw和λs分别表示冰、水和土体矿物的导热系数；ri、rw和rs分别表示单位体积中冰柱、水和土柱体积比，可依据式(10)计算.

土体的比热为

C=Cimi+Cwmw+Csms

(13)

其中，Ci、Cw和Cs分别表示冰、水和土体矿物的比热；mi、mw和ms分别表示单位体积中冰柱、水和土柱的质量比.

相变热为

(14)

其中，L为水的潜热；ρi为冰的密度；V为冻土的总体积. 冻土中各相的导热系数和比热如表1.

表1 冻土中不同相的热参数1)

1)因土质等条件不同，土的热参数表中未标明

2 不同温度下的热参数计算

饱和土体的干密度ρd与模型中的土颗粒体积Vs之间满足

(15)

将取自天津地铁5号线的粉质黏土装填进模型箱并进行饱和. 经测试，土体干密度约为1.80g/cm3，相对密度ds为2.72. 根据式(15)可计得Vs为6.618×109mm3，据此可得模型中的土柱半径为1 597.5mm. 制作3组含水率、干密度与模型箱中土体一致的饱和试样，并将试样置于低温试验箱；分别测定各试样在不同温度下的导热系数[19]，得到粉质黏土在不同温度下的导热系数，如图2.

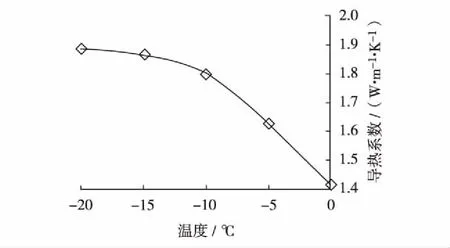
图2 随不同温度变化的导热系数Fig.2 Coefficients of thermal conductivity under different temperatures

既有研究表明，冻土热参数随温度的变化主要取决于冻土未冻水含量的变化[12,19-20]. 依据实测获取的导热系数，可计算出不同冻结时刻热参数模型中的未冻水含量，依据式(10)至式(14)可计算不同温度下冻土的比热和潜热值，结果如图3和图4.

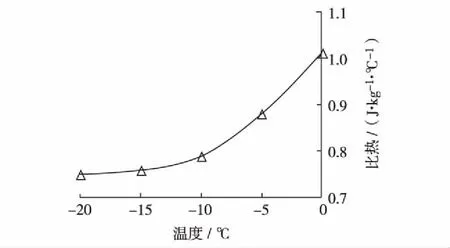
图3 随不同温度变化的比热Fig.3 Coefficients of specific heat under different temperatures

图4 相变潜热温度阶段曲线Fig.4 Curves of phase change latent heat of temperature

由图2至图4可知，随着冻结温度的降低，土体的导热系数逐渐增大，比热逐渐减小，冻土的导热系数和比热在高温冻土区间变化明显. 相变潜热发生在温度的一定区间而非0 ℃一点，且随温度降低，潜热余量渐减，这与实际情况吻合[10-11].

3 冻结试验及温度场数值计算

为有效度量由等效土柱模型获取的各热参数值在温度场计算中的预测精度，设计了模型箱双管冻结试验，依据相应试验条件和各热参数计算值进行ABAQUS数值计算，并将获取的温度场实测值与计算值进行了对比.

3.1 冻结试验

冻结试验采用2.0m×1.2m×1.0m的模型箱，在模型箱2.0m×1.2m面垂直插入Ф 42.00mm×0.96m的冻结管，在冻结管的法平面上设置若干测温点，冻结管和测温点布置的相对位置如图5.

图5 温度测点布置图(单位：mm)Fig.5 The temperature measurement point layout(unit：mm)

冻结试验中，冻结管提供(-25±0.5)℃冷端温度，模型箱周围设置有保温岩棉，模型箱底面与地面直接接触. 模型箱周围温度约为6.7 ℃，模型箱表面与空气对流换热系数取10W/(m2·℃).

3.2 温度场数值计算

依据冻结试验条件和表2的热参数取值，对模型箱中的温度场进行数值计算. 假定初始潜热发生在-2～0 ℃[18]，将其他温度阶段的潜热增量转化为比热进行计算.

表2 不同温度下的热参数取值

4 结果对比分析

利用ABAQUS软件进行冻土温度场的数值计算，得到冻结150 h的温度场云图切面(图6). 将各测点的温度场数值计算结果和模型箱实测值进行整理，结果如图7. 各测点实测值与计算值在不同冻结阶段的误差如表3.

图6 模拟值温度场云图Fig.6 (Color online) Simulated temperature field nephogram

图7 模拟值与实测值对比Fig.7 Comparison between simulated and measured values

Table 3 The error value of each point in different time ℃

由图7和表3可知，随着冻结时间的持续，各测点计算值与实测值之间的误差逐渐减小. 测点1位于两根冻结管之间，最先受到冷源影响，在冻结30 h前误差较大. 测点2和测点3分别位于测点1的上部和下部，模型箱上部空气与土体的对流换热及室温地面与土体的接触换热对测点影响较大；且比测点1距离冻结源远，在冻结30 h后区域出现一定误差. 测点4位于冻结管外部，单侧受冷源影响，土体温度下降较慢，在冻结80 h内误差均较大. 各点实测值与计算值最大误差在3.0 ℃以内，冻结60 h后土体实测值与计算值误差基本维持在0.3 ℃. 提出的基于最紧密排列土柱的热参数计算模型在温度场计算中的预测精度较高.

实测值与计算值在一定区间内存在一定温度点离散现象，但随着冻结的持续，两者趋于一致. 冻结初期实测值与计算值存在较大误差的原因可从以下方面分析：① 冻结过程中冻结管提供的冷端温度并不恒定；② 地面温度和室内温度变动引起的热量散失；③ 土体初温分布并不均匀，冻结过程中保温材料并非理想体；④ 土体碎散等结构特性在冻结初期尤为明显，依据土柱模型获取的热参数存在一定误差.

结 语

本研究分析了冻土温度场计算的影响因素，提出一种最紧密排列土柱的等效几何模型，土柱外部被自由水充满. 假定冻结在土柱围合区域的中心产生并呈柱状发展，根据任意时刻单元体内部土、水和冰的体积构成，建立了未冻水含量与导热系数之间的计算关系. 依据比热加权计算的原理，结合土的相对密度和水、冰的密度，获取了土柱模型在不同冻结时刻各相的质量比，进而确定了未冻水含量与比热之间的计算关系. 依据不同冻结时刻土柱模型中的未冻水含量，建立了潜热随冻结时间的变化关系. 依据实测粉质黏土的导热系数，结合土柱等效模型获取比热、潜热随温度的变化关系. 将随不同温度变化的导热系数、比热、潜热值代入数值计算软件ABAQUS，获取冻土瞬态温度场的计算值. 将该计算值与实测值对比表明，基于最紧密排列土柱模型计算的热参数能够较好地预测冻土温度场.

/ References：

[1] 原喜忠, 李 宁, 赵秀云, 等. 非饱和(冻)土导热系数预估模型研究[J]. 岩土力学, 2010, 31(9): 2689-2694. Yuan Xizhong, Li Ning, Zhao Xiuyun, et al. Study of thermal conductivity model for unsaturated unfrozen and frozen soils[J]. Rock and Soil Mechanics, 2010, 31(9): 2689-2694.(in Chinese)

[2] 蔡海兵, 黄以春, 庞涛. 地铁联络通道三维冻结温度场有限元分析[J]. 铁道科学与工程学报, 2015, 12(6): 1436-1443. Cai Haibing，Huang Yichun，Pang Tao. Finite element analysis on 3D freezing temperature field in metro connected aisle construction[J].Journal of Railway Science and Engineering, 2015, 12(6): 1436-1443.(in Chinese)

[3] 何 敏, 李 宁, 高焕焕,等. 带相变瞬态温度场问题的扩展有限元解析[J]. 冰川冻土, 2016, 38(4): 1044-1051. He Min, Li Ning, Gao Huanhuan, et al. Extended finite element method analysis for the transient temperature field with phase change[J]. Journal of Glaciology and Geocrylogy, 2016, 38(4): 1044-1051.(in Chinese)

[4] 胡向东, 陈 锦, 汪 洋,等. 环形单圈管冻结稳态温度场解析解[J]. 岩土力学, 2013, 34(3): 874-880. Hu Xiangdong, Chen Jin, Wang Yang, et al. Analytical solution to steady-state temperature field of single-circle-pipe freezing[J]. Rock and Soil Mechanics, 2013, 34(3): 874-880.(in Chinese)

[5] 陶兆祥, 张景森. 大含水(冰)量融冻土导热系数的测定研究[J]. 冰川冻土, 1983, 5(2): 75-80. Tao Zhaoxiang, Zhang Jingsen. The thermal conductivity of thawed and frozen soils with high water (ice) content[J]. Journal of Glaciology and Geocryology, 1983, 5(2): 75-80.(in Chinese)

[6] 刘焕宝, 张喜发, 赵意民, 等. 冻土导热系数热流计法模拟试验及成果分析[J]. 冰川冻土, 2011, 33(5): 1127-1131. Liu Huanbao, Zhang Xifa, Zhao Yimin, et al. Frozen soil thermal conductivity determined by using heat-flow meter: simulation experiment and result analysis[J]. Journal of Glaciology and Geocryology, 2011, 33(5): 1127-1131.(in Chinese)

[7] 周家作, 韦昌富, 魏厚振,等. 线热源法测量冻土热参数的适用性分析[J]. 岩土工程学报, 2016, 38(4): 681-687. Zhou Jiazuo, Wei Changfu, Wei Houzhen, et al. Applica- bility of line heat source method in measuring thermal parameters of frozen soil[J] Chinese Journal of Geote- chnical Engineering, 2016, 38(4): 681-687.(in Chinese)

[8] 陈 琳, 喻文兵, 杨成松, 等. 基于微观结构的青藏高原风积沙导热系数变化机理研究[J]. 冰川冻土, 2014, 36(5): 1220-1226. Chen Lin, Yu Wenbing, Yang Chengsong, et al. Conductivity of aeolian sand on the Tibetan Plateau based on microstructure[J]. Journal of Glaciology and Geocryology, 2014, 36(5): 1220-1226.(in Chinese)

[9] 张 楠, 夏胜全, 侯新宇,等. 土热传导系数及模型的研究现状和展望[J]. 岩土力学, 2016, 37(6): 1550-1562. Zhang Nan, Xia Shengquan, Hou Xinyu, et al. Review on soil thermal conductivity and prediction model[J]. Rock and Soil Mechanics, 2016, 37(6): 1550-1562.(in Chinese)

[10] 赵 刚, 陶夏新, 刘 兵. 原状土冻融过程中水分迁移试验研究[J]. 岩土工程学报, 2009, 31(12): 1952-1957. Zhao Gang, Tao Xiaxin, Liu Bing. Experimental study on water migration in undisturbed soil during freezing and thawing process[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1952-1957.(in Chinese)

[11] 王铁行, 刘自成, 卢 靖. 黄土导热系数和比热容的实验研究[J]. 岩土力学, 2007, 28(4): 655-658. Wang Tiehang, Liu Zicheng, Lu Jing. Experimental study on coefficient of thermal conductivity and specific volume heat of loess[J]. Rock and Soil Mechanics, 2007, 28(4): 655-658.(in Chinese)

[12] 冷毅飞, 张喜发, 杨凤学,等. 冻土未冻水含量的量热法试验研究[J]. 岩土力学, 2010, 31(12): 3758-3764. Leng Yifei, Zhang Xifa, Yang Fengxue, et al. Experimental research on unfrozen water content of frozen soils by calorimetry[J]. Rock and Soil Mechanics, 2010, 31(12): 3758-3764.(in Chinese)

[13] 孙斌祥, 徐斅祖, 赖远明, 等. 块石的热扩散系数和导热系数确定方法[J]. 冰川冻土, 2002, 24(6): 790-795. Sun Binxiang, Xu Xiaozu, Lai Yuanming, et al. Determination of Thermal Diffusivity and Conductivity on Ballast[J]. Journal of Glaciology and Geocryology, 2002, 24(6): 790 -795.(in Chinese)

[14] 肖衡林, 吴雪洁, 周锦华. 岩土材料导热系数计算研究[J]. 路基工程, 2007(3): 54-56. Xiao Henglin, Wu Xuejie, Zhou Jinhua. Study on calculation of thermal conductivity of geotechnical materials[J]. Subgrade Engineering, 2007(3): 54-56.(in Chinese)

[15] 马 巍, 王大雁. 中国冻土力学研究50 a回顾与展望[J]. 岩土工程学报, 2012, 34(4): 625-640. Ma Wei, Wang Dayan. Studies on frozen soil mechanics in China in past 50 years and their prospect[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 625-640.(in Chinese)

[16] Johansen B A, Branko L. Frozen ground engineering[M]. New Jersey, USA: John Wiley & Son, 2004.

[17] 王彦洋. 冻土的热参数与土冻结过程的热力耦合分析[D]. 天津: 天津城建大学, 2015. Wang Yanyang. The analysis of thermal parameters for frozen soil and coupled thermal-stress for the process of soil freezing[D]. Tianjin: Tianjin Chengjian University, 2016.(in Chinese)

[18] 刘 月, 王正中, 王 羿, 等. 考虑水分迁移及相变对温度场影响的渠道冻胀模型[J]. 农业工程学报, 2016, 32(17): 83-88. Liu Yue, Wang Zhengzhong, Wang Yi, et al. Frost heave model of canal considering influence of moisture migration and phase transformation on temperature field[J]. Journal of the Chinese Society of Agricultural Engineering, 2016, 32(17): 83-88.(in Chinese)

[19] 于 珊, 李顺群, 冯慧强. 土的导热系数与其干密度、饱和度和温度的关系[J]. 天津城建大学学报, 2015(3): 172-176. Yu Shan, Li Shunqun, Feng Huiqiang. Relationship among soil’s thermal conductivity, dry density, saturation and temperature[J]. Journal of Tianjin Chengjian University, 2015(3): 172-176.(in Chinese)

[20] 王丽霞, 胡庆立, 凌贤长, 等. 青藏铁路冻土未冻水含量与热参数试验[J]. 哈尔滨工业大学学报, 2007, 39(10): 1660-1663. Wang Lixia, Hu Qingli, Ling Xianchang, et al. Test study on unfrozen water content and thermal parameters of qinghai-tibet railway frozen silty clay[J]. Journal of Harbin Institute of Technology, 2007, 39(10): 1660-1663.(in Chinese)

【中文责编：坪 梓；英文责编：之 聿】

2017-01-11；Accepted：2017-02-23

Professor Li Shunqun. E-mail: lishunqun@yeah.net

Calculation of thermal parameters of frozen soil based on the closely spaced soil column model

Chen Zhixiang1,2, Li Shunqun1,2, Xia Jinhong3, Wang Kai1,2, and Gui Chao3

1) School of Civil Engineering, Tianjin Chengjian University, Tianjin 300384, P.R.China 2) Tianjin Key Laboratory of Soft Soil Characteristics and Engineering Environment, Tianjin 300384, P.R.China 3) School of Civil Engineering and Architecture, Xinxiang University, Xinxiang 453003, Henan Province, P.R.China

In order to evaluate the influence of thermal parameters on the calculation of transient temperature field of saturated frozen soil, the influencing factors of frozen soil temperature field are analyzed. A kind of soil column geometric model is put forward, and the outside of the soil column is filled with pore water. Assuming that the freezing occurs at the center of the enclosing area of the soil column and develops in column form, according to the calculation of the volume of soil, water and ice in the body at any time, and the calculation method of the soil thermal conductivity of Johansen, the relationship between the unfrozen water content and the thermal conductivity is established. According to the weighting calculation principle of specific heat and the relative density of soil and the density of water and ice, the mass ratio of soil column in different freezing time is obtained, then the relationship between unfrozen water content and specific heat is determined. According to the unfrozen water content of soil column model at different freezing time, the relationship between latent heat and freezing time is established. Based on the measured thermal conductivity and the soil column model, the relationship between specific heat and latent heat with negative temperature is obtained. The thermal conductivity, specific heat and latent heat of frozen soil under different negative temperature conditions obtained from the model are analyzed by numerical calculation software ABAQUS, and the calculated values of frozen soil temperature field are obtained. Comparing the calculated values with the measured results, it is shown that the thermal parameters obtained from the model can predict the temperature field of frozen soil.

geotechnical engineering; frozen soil; thermal parameters; soil column model; temperature field; unfrozen water; latent heat

：Chen Zhixiang, Li Shunqun, Xia Jinhong,et al. Calculation of thermal parameters of frozen soil based on the closely spaced soil column model[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(4): 393-399.(in Chinese)

TU 752

A

10.3724/SP.J.1249.2017.04393

国家自然科学基金资助项目(41472253)；天津市自然科学基金重点资助项目(16JCZDJC39000)；天津市建设系统科学技术资助项目(2016-25)

陈之祥(1990—)，男，天津城建大学硕士研究生. 研究方向：土的本构关系. E-mail：chen_zhixiang@126.com

Foundation：National Natural Science Foundation of China (41472253); Key Project of Natural Science Foundation of Tianjin City (6JCZDJC39000); Tianjin Construction System Science and Technology Project Development Plan (2016-25)

引 文：陈之祥, 李顺群, 夏锦红，等.基于紧密排列土柱模型的冻土热参数计算[J]. 深圳大学学报理工版，2017，34(4)：393-399.