相互垂直裂缝应力阴影的影响因素及规律

2017-07-18汪道兵周福建葛洪魁SergioZlotnik杨向同彭金龙

深圳大学学报（理工版） 2017年4期

汪道兵，周福建，葛洪魁，Sergio Zlotnik，杨向同，彭金龙

1)中国石油大学(北京)非常规天然气研究院，北京100249；2)西班牙加泰罗尼亚理工大学土木工程学院，巴塞罗那E-08034，西班牙；3)中国石油勘探开发研究院采油工程研究所，北京100083；4)中国石油塔里木油田分公司，新疆维吾尔自治区库尔勒841000；5)中国石油大庆油田有限责任公司第二采油厂，黑龙江大庆163414

【环境与能源 / Environment and Energy】

相互垂直裂缝应力阴影的影响因素及规律

汪道兵1,2,3，周福建1，葛洪魁1，Sergio Zlotnik2，杨向同4，彭金龙5

基于弹性力学理论，采用Galerkin有限元数值离散化方法，编制Matlab有限元程序，数值模拟两条相互垂直裂缝干扰时的“应力阴影”分布状态，其主应力与主方向分布具有关于交点(坐标原点)的对称性特征．分析了流压比值、孔隙压力、缝面流压及水平应力差值等因素对两缝间主应力及主方向的影响，通过改进变排量施工、改变压裂液黏度、油气井开采降低孔隙压力和增大注入液量等工艺，发挥应力阴影效应的优点，增加复杂缝网形成的可能性．

应力干扰；缝网压裂；垂直裂缝；有限元方法；转向剂；可降解纤维；流体压力；流固耦合；线弹性力学

页岩气和致密气等非常规油气藏要通过分簇射孔、分级完井和分段水力压裂形成复杂裂缝才能获得经济产能，而每次形成的人工裂缝将会改变裂缝周围的应力场分布，当裂缝间距较近时，将会发生应力阴影效应，即后续人工裂缝的起裂与扩展会受到先前产生裂缝应力场的影响[1]．正确利用应力阴影效应将有助于合理设计页岩气井的完井方式、压裂工艺和提高气井产能．

近年来，不少学者研究了水力压裂引起的应力阴影效应．Suppachoknirun等[1]数值模拟了天然裂缝、裂缝间距、岩石力学性质和就地应力条件等因素对多条平行裂缝产生的应力阴影的影响规律，提供了一种定量优化页岩完井方式的方法，理解裂缝间距对应力阴影效应的影响，促进复杂裂缝的形成．Skomorowski等[2]研究了非常规气藏多级水力压裂(multi-stage hydraulic fracturing, MSHF)过程中的应力阴影效应，提供了优化裂缝间距的可能性，得出了应力差改变对完井方式的影响，指出非常规油气藏水力压裂期间波动的瞬时停泵压力(instantaneous shut-in pressure, ISIP)和破裂压力很好地体现了应力阴影干扰现象，并可能影响延伸裂缝的重新定向．Wu等[3]分析了多条平行裂缝沿水平井筒的非均匀扩展问题，提供了控制多条裂缝同时扩展的新视角．Stepanova等[4]推导了无限大弹性体中裂缝周围的应力场计算公式．Damjanac等[5]的室内实验证实，油气井压裂后，孔隙压力在前次裂缝周围成椭圆形状分布，随着油气生产的进行，孔隙压力在裂缝周围的分布将很不均匀，从而改变了地层中裂缝周围的孔隙压力梯度，导致整个储层内的地应力重新分布．Kumar等[6]用流固耦合的二维数值模型研究了前次裂缝周围孔隙压力随时间变化的影响，并证明了长期生产能逐渐改变地应力场，使应力发生90°反转．Pankaj等[7-9]根据试验和模拟研究认为，地层中存在的支撑裂缝将改变井眼附近应力分布，使重复压裂裂缝的启裂方位垂直于初次裂缝方位，离开井眼一定范围再发生转向，以平行于初次裂缝方位延伸．Morales等[10]在应力轨迹理论的基础上通过对影响重复压裂裂缝扩展的无因次量的分析，得到了重复压裂裂缝延伸的轨迹．汪道兵等[11-12]系统地研究了引起垂直裂缝井重复压裂前原地应力场变化的主要因素，建立了重复压裂时的总应力场计算模型．

前人对水力压裂引起的应力场的研究对象多集中于单缝或平行裂缝，多数以Sneddon解析解为基础进行数值模拟，而页岩水力压裂以形成缝网为主，但目前对垂直交叉裂缝形成应力阴影报道较少[1-9]．本研究从有限元变分原理出发，采用Galerkin有限元数值离散化方法，基于弹性力学理论，编制应力平衡方程的有限元程序，数值模拟了两条相互垂直裂缝干扰时的“应力阴影”分布状态，研究了两裂缝流压比值、孔隙压力、缝面流压和水平地应力差等因素对“应力阴影”的影响．

1 物理模型

两条垂直裂缝间形成应力干扰的物理模型如图1，其假设条件[11-14]如下：

1)渗透率各向同性的有限地层中间存在两条相互垂直的人工裂缝，它们缝长、缝宽均相同，且数值保持不变化，半缝长记为L；

2)问题简化为二维平面应变问题；

3)外边界地层地应力最大、最小水平主应力分别为σH和σh；

4)液体作用在两缝面上的流压分别为p11和p21；

5)假设应力干扰在地层温度条件下进行，即视应力干扰过程为等温过程；

6)不考虑流固耦合效应，即固定两缝面压力情况下，研究两垂直缝间的干扰效应；

7)原始地层孔隙压力为pp，地层流体微可压缩，不考虑应力变化引起的岩石基质变形对孔压的影响；

8)边界Γ=ΓL∪ΓR∪ΓT∪ΓB∪ΓF，ΓL和ΓR分别为远场左、右边界，ΓT和ΓB分别为上、下边界，4个边界上的远场应力分别为σH和σh，ΓF为两裂缝边缘，其上流压为p11与p21．

图1 两条垂直裂缝干扰的物理模型Fig.1 (Color online) The physical model of two parallel disturbed fractures

2 数学模型

2.1 控制方程

根据弹性力学理论，应力平衡方程[13-14]为

σij,j+bi=0

(1)

其中，σij为二阶Cauthy应力张量；bi为一阶体积力张量；i,j=1, 2．

假设多孔介质为线弹性变形，应力应变服从小变形假设，则应力应变张量关系式[15-16]为

σij=Dijklεkl

(2)

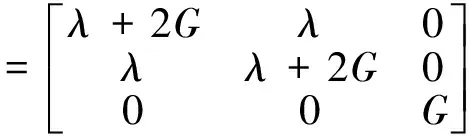
根据有效应力概念，柯西应力可以分解成两部分，代表流体孔隙压力对固体基质产生的效应[17]，即

σeff=σ-αppI

(3)

其中，σeff为有效应力张量；α为Biot弹性常数，α∈[0,1]；pp为地层原始孔隙压力；I为单位张量．

应变与位移张量间关系式[13-14,17]为

(4)

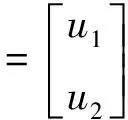
2.2 边界条件

1)左边界ΓL和右边界ΓR：t1=-σH；

2)上边界ΓT与下边界ΓB：t2=-σh；

3)第1条裂缝：t1=0,t2=p1；

4)第2条裂缝：t1=0,t2=p2．

2.3 有限元离散化方法

2.3.1 变分形式

根据有限元变分理论，设Ω为图1中的区域，对任意的测试函数wi∈Vi={wi|wi=0, 在Γqi上}，Vi为变分空间，Γqi对应区域Ω中的位移边界条件(数学上为Dirichlet条件)的边，得出应力平衡方程的变分形式15-16]为

a(w,u)=(w,b)+(w,t)Γ

(5)

2.3.2 应力平衡方程的Galerkin离散化

Kd=F

(6)

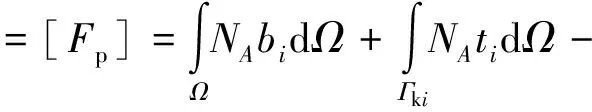
ndof为自由度小数.

用Matlab高级语言编制了有限元计算程序，由于三角形单元节点数较多(12 044个)，刚度矩阵K采用稀疏矩阵方式来存储，即K=sparse(allJ,allI,allK)，allI和allJ表示非零元素allK的指标[19]；有限元算法求解出方程(6)后，得出位移节点分布，再根据本构关系可以分别求出应力与应变分量，最后分别得出主方向与主应力的大小分布，计算公式[13-14]为

(7)

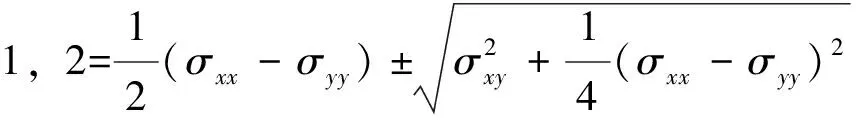
(8)

其中，θ表示主方向；σ1和σ2表示两水平主应力大小，且σ1>σ2，进而可以得出区域中的主方向与主应力的平面分布状态(本研究只计算最大主应力σ1)．

2.4 模型验证

取与表1相同的最大和最小水平应力值，孔隙压力和井壁流压均设为0，采用式(6)中有限元离散化结果模拟了半径为0.1m直井井眼在1m处的切向应力大小，并与弹性力学中的周向应力解析解对比[11-13,20]，如图2．有限元数值解与解析解一致，验证了本模型有限元数值解的可靠性．

表1 基本输入参数

图2 周向应力的有限元解与解析解比较(r=1 m)Fig.2 (Color online) Comparison of finite element solution and analytical solution of hoop stress (r=1 m)

3 有限元数值模拟结果

为分析两条垂直裂缝间应力干扰的影响，分别模拟了它们的主应力、主方向分布，并对孔隙压力、缝面流体压力、两缝面流压比和水平应力差值进行了因素敏感性分析．

3.1 主方向与主应力分布

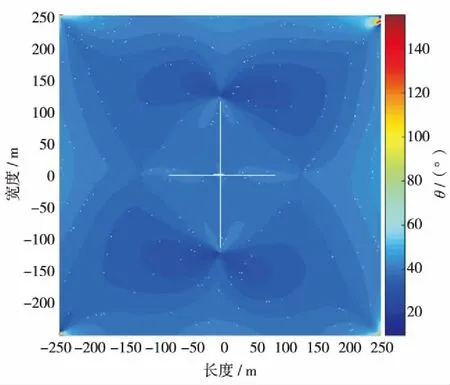
图3 主方向平面分布图Fig.3 (Color online) The 2D distribution of principle angle

按表1中的基本参数，以两垂直裂缝交点为原点，x轴沿水平向右方向，y轴沿垂直向上方向建立直角坐标系，分别模拟了主方向与主应力二维平面分布图，结果如图3和图4．可看出它们的分布具有关于交点(坐标原点)的对称性特征，即第一、三象限和第二、四象限分布基本相同．在垂直方向裂缝(对应图1的第2条)端部呈现了明显的应力集中现象，而水平方向裂缝端部的应力集中现象不明显(较弱)，可能是两裂缝应力干扰叠加后应力集中现象减弱的结果．但是第1条裂缝部分(端部到中间部位)主应力值较小(图4中圆圈标记区域)，主方向值不同于其他区域，可利用此部分“应力阴影”效应，采用缝端端部暂堵转向压裂工艺，在第1条裂缝处发生人工裂缝转向，从而产生新裂缝，促进复杂缝网形成的可能性[12-13,21-25]．

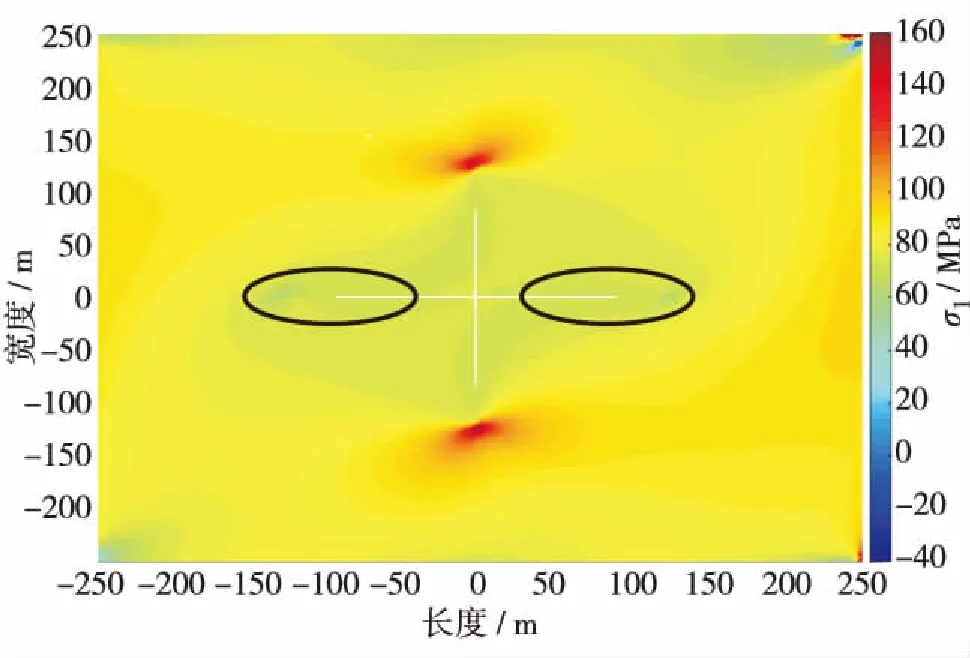
图4 主应力平面分布图Fig.4 (Color online) The 2D distribution of principle stress

3.2 两缝面流体压力比

图5 不同流压比值下主应力与主方向变化曲线Fig.5 (Color online) The relationships between fluid pressure ratio and principle stress, principle angle

输入表1参数，改变两裂缝内流压比值，其他参数保持不变，模拟了P1和P2两点处的主应力值与主方向随流压比值的变化规律，参考表1中50MPa缝内流压值，结果如图5，纵坐标表示归一化主应力与归一化主方向．从图5可见，随着两缝内流压比值增大，主应力和主方向均呈现线性单调递减趋势(P2点主应力变化较缓慢)．说明改变两缝内压力分布，可以诱使主方向和主应力发生变化，从而利用两缝间应力干扰效应，促使新的人工裂缝形成，形成复杂缝网；现场可以多次停泵、变排量施工，使两缝内压力发生波动，或者注入纤维等暂堵转向剂，提高缝内净压力，诱使缝间流压变化，形成缝间干扰，引发复杂缝网形成[21-25]．

3.3 孔隙压力

按表1 中参数，取不同的地层孔隙压力值，其他参数保持不变，模拟了P1和P2两点处的不同孔隙压力下主应力与主方向的变化，参考表1中50MPa孔隙压力，结果如图6，纵坐标表示归一化主应力与归一化主方向．从图6可见，随着孔隙压力增加，两点处的主应力主方向均单调递增，说明增大或减小地层孔隙压力可诱使两缝间应力场变化，因此可通过开采降低孔隙压力或注水提高孔隙压力办法，促使人工裂缝重新定向[21-25]．

图6 不同地层孔隙下主应力与主方向变化曲线Fig.6 (Color online) The relationships between pore pressure and principle stress, principle angle

3.4 缝面流体压力

如表1 中参数，保持两裂缝中流压相同，改变作用于缝面上流体压力大小，模拟P1和P2两点处的主应力与主方向随流压的变化规律，参考表1中50MPa缝内流体压力，结果如图7，纵坐标表示归一化主应力与归一化主方向．随着流体压力增加，主应力和主方向呈现线性减小趋势，说明可以通过改变压裂液黏度、变排量施工的办法来增强缝间干扰，促使裂缝重新定向，引导复杂人工缝网的形成[21-25]．

图7 不同流压下主应力与主方向变化曲线(两缝流压相同)Fig.7 (Color online) The relationships between fluid pressure and principle stress, principle angle (The two fractures have the same fluid pressure.)

3.5 远场水平应力差值

如表1 中参数，改变远场水平应力差值大小，其他参数保持不变，模拟P1和P2两点处的主应力与主方向随水平应力差值的变化规律，以表1中水平应力差值为参考值，结果如图8，纵坐标表示归一化主应力与归一化主方向．随着水平应力差值增加，主方向线性减小，主应力线性增大，说明较小应力差值水平下，主应力值较小，此时人工裂缝较易重新定向，可通过纤维暂堵转向压裂办法，诱使复杂人工缝网的形成[21-25]．

图8 不同水平应力差值下的主应力与主方向变化曲线Fig.8 (Color online) The relationships between horizontal stress difference and principle stress, principle angle

4 现场实例

A井是塔里木盆地塔北隆起轮南奥陶系潜山背斜西围斜哈拉哈塘富油气区带上的一口探井，完井方式为裸眼完井，井型为直井，目的层是奥陶系一间房组及鹰山组一段，酸压改造目的层段为奥陶系6 618.5～6 700.0m．该井油气显示情况较差，物探资料平面图反映井眼向南东偏移串珠中心55m．最大水平主应力为136～153MPa，平均值为144.8MPa；最小水平主应力为136～152MPa，平均值为143.7MPa，应力差值0～3MPa，平均值仅为1.1MPa．本区最大主应力方向为NE40°左右，A井偶极声波各向异性玫瑰图显示储层段最大主应力方向为NW300°—NW330°，双井径基本无差异，6 536～6 748m井段最大水平主应力与最小水平主应力差值较小(均值仅为1.06MPa)．根据岩石力学规律，人工裂缝的起裂和延伸方向存在不确定性，可能影响酸压沟通储集体．

由于A井油层段的应力差值较小，根据前面分析，可以采用纤维暂堵转向压裂技术，改变缝内净压力分布，促使复杂缝网的形成，从而提高沟通缝洞储集体的机率．根据施工曲线，绘制出泵注两级压裂液过程中的泵压和排量曲线，如图9，第1级压裂破裂后，泵压持续升高(由76.8MPa升至88.4MPa)，未沟通到储集体；泵注第2级压裂液过程中，排量低于第1级，但泵压高于第1级，两次泵压不相同，说明可能是产生了转向裂缝导致两级泵压有差异．

图9 泵注第1级和第2级压裂液井口压力和排量对比Fig.9 (Color online) The comparison of pump pressure and flow during the first and the second stage

从图9中读出两级压裂的破裂压力(转换成井底压力)，第2级破裂压力比第1级破裂压力高出约25MPa，根据转向判定模拟结果，第2级破裂压力至少比第1级高出12.2MPa才能产生转向裂缝，两次张性破裂压力不同，结合注酸后泵压大幅度下降及压后返排残酸情况，有力地说明第2级压裂产生了转向裂缝．

根据施工曲线，绘制出纤维进入地层后的泵压和排量曲线，如图10，可以看出纤维进入地层后泵压升高了20MPa，说明纤维起到了暂堵裂缝作用，之后注入第2级压裂液，破裂点明显．

A井酸压施工虽有明显沟通，但储集体内流体为水．酸压后4mm油嘴求产，油压0.45MPa，产少量气，产水23.92m3/d．测试结论为含气水层．

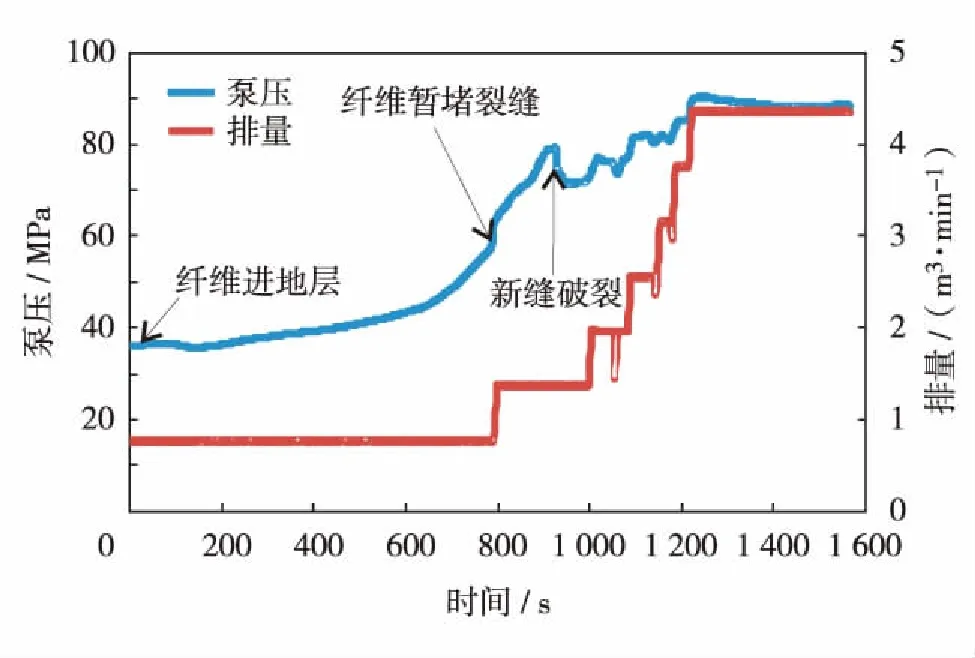
图10 纤维进地层后泵压和排量曲线Fig.10 (Color online) The pump pressure and flow rate after fiber enters into the formation

5 结论

综上研究可见：

1) 本研究根据有限元变分理论和弹性力学理论，采用Galerkin有限元离散化方法，编制了两条垂直裂缝间应力干扰的有限元程序，得出了主应力和主方向的平面分布图．

2)模拟了主应力与主方向的平面分布图，它们的分布具有关于交点(坐标原点)的对称性特征．其中一条裂缝部分(端部到中间部位)主应力值较小，主方向值变化较强，可利用此部分“应力阴影”效应，采用端部暂堵转向压裂工艺，产生新裂缝，促进复杂缝网形成的可能性．

3) 分析了流压比值、孔隙压力、缝面流压及水平应力差值等因素对两缝间主应力及主方向的影响规律，可通过改进变排量施工、改变压裂液黏度、油气井开采降低孔隙压力和增大注入液量等工艺，利用应力阴影效应，提高复杂缝网形成的可能性．

/ References：

[1] Suppachoknirun T, Tutuncu A N, Kazemi H. Evaluation of multistage hydraulic fracturing techniques for production optimization in naturally fractured reservoirs using coupled geomechanics fracture and flow model[C]// International Petroleum Technology Conference. Bangkok, Thailand: International Petroleum Technology Conference, 2016: 1-24.doi: IPTC-18916-MS.

[2] Skomorowski N, Dussealut M B, Gracie R.The use of multistage hydraulic fracture data to identify stress shadow effects[C]// 49th US Rock Mechanics/Geomechanics Symposium. San Francisco, USA：American Rock Mechanics Association，2015:1-8. doi: ARMA-2015-624.

[3] Wu Kan, Olson J, Balhoff M T,et al.Numerical analysis for promoting uniform development of simultaneous multiple fracture propagation in horizontal wells[C]// SPE Annual Technical Conference and Exibition. Houston, USA：Society of Petroleum Engineers，2015:1-9. doi: SPE-174869-MS.

[4] Stepanova L, Roslyakov P. Multi-parameter description of the crack-tip stress field: Analytic determination of coefficients of crack-tip stress expansions in the vicinity of the crack tips of two finite cracks in an infinite plane medium[J]. International Journal of Solids and Structures, 2016, 100/101: 11-28.

[5] Damjanac B, Cundall P. Application of distinct element methods to simulation of hydraulic fracturing in naturally fractured reservoirs[J]. Computers and Geotechnics, 2016, 71: 283-294.

[6] Kumar D, Ghassemi A. 3D poroelastic simulation and analysis of multiple fracture propagation and refracturing of closely-spaced horizontal wells[C]// 50th US Rock Mechanics/Geomechanics Symposium. Houston, USA: American Rock Mechanics Association, 2016: 1-12. doi: ARMA-2016-136.

[7] Pankaj P, Gakhar K, Lindsay G. When to refrac? Combination of reservoir geomechanics with fracture modeling and reservoir simulation holds the answer[C]// SPE Asia Pacific Oil & Gas Conference and Exhibition. Perth, Australia: Society of Petroleum Engineers, 2016: 1-21. doi:SPE-182161-MS.

[8] Curnow J S, Tutuncu A N. A coupled geomechanics and fluid flow modeling study for hydraulic fracture design and production optimization in an eagle ford shale oil reservoir[C]// SPE Hydraulic Fracturing Technology Conference. The Woodlands, USA: Society of Petroleum Engineers, 2016: 1-12. doi: SPE-179165-MS.

[9] Bartko K, McClelland K, Sadykov A, et al. Holistic approach to engineered diversion-aided completion providing new method of fracture isolation[C]// SPE Hydraulic Fracturing Technology Conference and Exhibition. The Woodlands, USA: Society of Petroleum Engineers, 2017:1-14. doi: SPE-184824-MS.

[10] Cafaro D C, Drouven M G, Grossmann I E. Optimization models for planning shale gas well refracturetreatments[J]. AIChE Journal, 2016, 62(12): 4297-4307.

[11] 汪道兵, 葛洪魁, 周福建, 等. 注入流体诱导应力场模拟计算[J]. 东北石油大学学报, 2015, 39(2): 85-93. Wang Daobing, Ge Hongkui, Zhou Fujian, et al. Numerical simulation of the injected fluid induced stress field[J]. Journal of Northeast Petroleum University, 2015, 39(2): 85-93.(in Chinese)

[12] 汪道兵. 直井纤维暂堵转向压裂裂缝启裂与延伸数学模型研究[D]. 成都: 成都理工大学, 2013. Wang Daobing. Study on the mathematical model about the fiber temporary plugging diverting fracturing crack initiation and propagation of the vertical wells[D]. Chengdu: Chengdu University of Technology, 2013.(in Chinese)

[13] Fjar E, Holt R M, Raaen A M, et al. Petroleum related rock mechanics[M]. 2nd ed.. Amsterdam, The Netherlands: Elsevier, 2008.

[14] John Conrad Jaeger, Neville G W Cook, Robert Zimmerman. Fundamentals of rock mechanics[M]. 4th ed.. Oxford, UK: Wiley-Blackwell, 2007.

[15] Zienkiewicz O C, Taylor R L, Zhu J Z. The finite element method: its basis and fundamentals[M]. 7th ed.. Oxford, UK: Elsevier, 2013.

[16] Hughes T J. The finite element method: linear static and dynamic finite element analysis[M]. New Jersey, USA: Courier Corporation, 2012.

[17] Pogacnik J, Elsworth D, O’Sullivan M, et al. A damage mechanics approach to the simulation of hydraulic fracturing/shearing around a geothermal injection well[J]. Computers and Geotechnics, 2016,71:338-351.

[18] Detournay E. Mechanics of hydraulic fractures[J]. Annual Review of Fluid Mechanics, 2016, 48(1): 311-339.

[19] Signorini M, Zlotnik S, Díez P. Proper Generalized Decomposition solution of the parameterized Helmholtz problem: application to inverse geophysical problems[J]. International Journal for Numerical Methods in Engineering, 2017, 109(8): 1085-1102.

[20] 周福建, 汪道兵, 伊向艺, 等. 迫使碳酸盐岩油气藏裂缝向下延伸的酸压技术[J]. 石油钻采工艺, 2012, 34(6): 65-68. Zhou Fujian, Wang Daobing, Yi Xiangyi, et al. Acid fracturing technology forcing fracture to propagate downward in carbonate reservoirs[J]. Oil Drilling & Production Technology, 2012, 34(6): 65-68.(in Chinese)

[21] 周福建, 伊向艺, 杨贤友, 等. 提高采收率纤维暂堵人工裂缝动滤失实验研究[J]. 钻采工艺, 2014, 37(4): 83-86. Zhou Fujian, Yi Xiangyi, Yang Xianyou, et al. Dynamic filtration experiment study on EOR fiber on bridging the artificial fracture[J]. Drilling & Production Technology, 2014, 37(4): 83-86.(in Chinese)

[22] 汪道兵, 周福建, 葛洪魁, 等. 纤维暂堵人工裂缝附加压差影响因素分析[J]. 科技导报, 2015, 33(22): 73-77. Wang Daobing, Zhou Fujian, Ge Hongkui, et al. Analysis of factors influencing additional pressure drop of fiber-assisted temporary blocking of an artificial fracture[J]. Science and Technology Review, 2015, 33(22):73-77.(in Chinese)

[23] Wang Daobing, Zhou Fujian, Ding Wei, et al. A numerical simulation study of fracture reorientation with a degradable fiber-diverting agent[J]. Journal of Natural Gas Science and Engineering, 2015, 25: 215-225.

[24] Wang Daobing, Zhou Fujian, Ge Hongkui, et al. An experimental study on the mechanism of degradable fiber-assisted diverting fracturing and its influencing factors[J]. Journal of Natural Gas Science and Engineering, 2015, 27(1): 260-273.

[25] Gomaa A M, Spurr N, Pirogov A, et al. Combining soluble particle diverter with specially engineered proppant to enhance fracture complexity and post-fracture conductivity[C]// SPE Annual Technical Conference and Exhibition. Dubai, UAE: Society of Petroleum Engineers, 2016: 1-14. doi: SPE-181486-MS.

【中文责编：晨兮；英文责编：天澜】

2016-08-03；Revised：2017-03-18；Accepted：2017-04-20

Professor Zhou Fujian. E-mail: zhoufj@cup.edu.cn

The main factors and rules of stress shadow of perpendicular cracks

Wang Daobing1,2,3, Zhou Fujian1, Ge Hongkui1, Sergio Zlotnik2, Yang Xiangtong4, and Peng Jinlong5

1) Unconventional Natural Gas Research Institute, China University of Petroleum, Beijing 102249, P.R.China 2) School of Civil Engineering, Technical University of Catalonia, Barcelona E-08034, Spain 3) Institute of Oil Production Engineering, Research Institute of Exploration & Development, PetroChina, Beijing 100083, P.R.China 4) Tarim Oilfield Company, PetroChina, Kuerle 841000, Xinjiang Uygur Autonomous Region, P.R.China 5) The Second Oil Extraction Plant of Daqing Oilfield Company Limited, PetroChina, Daqing 163414, Heilongjiang Province, P.R.China

Based on elasticity theory, we use numerical Galerkin finite element discretization method and implement Matlab finite element code to simulate “stress shadow” distributions of mutual orthogonal fractures. The principal stress and principal distributions have the symmetry characteristic on the intersection (coordinate origin). The relationships between stress shadow and flow pressure ratio, pore pressure, fluid pressure and horizontal stress contract are analyzed, respectively. By these techniques of variable displacement construction, changing the viscosity of the fracturing fluid, exploitation of oil and gas wells changing pump rate and fracturing fluid viscosity, reducing pore pressure and increasing the injection volume, taking the advantages of shadow effect, it is likely to produce a complex fracture network.

stress interference; fracture network fracturing; perpendicular crack; finite element method; diverting agent; degradable fiber; fluid pressure; fluid-solid coupling; linear elastic mechanics

：Wang Daobing, Zhou Fujian, Ge Hongkui, et al. The main factors and rules of stress shadow of perpendicular cracks[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(4): 344-351.(in Chinese)

TE 355

10.3724/SP.J.1249.2017.04344

国家重点基础研究发展规划资助项目(2015CB250903)；国家自然科学基金资助项目(51490652)；“十三五”国家科技重大专项资助项目(2016ZX05030-005)；中国石油大学(北京)科研基金资助项目(2462016YXBS10)

汪道兵(1985—)，男，中国石油大学(北京)博士研究生．研究方向：非常规储层缝网形成与控制机理.E-mail: 0546wdb@163.com

Foundation：National Basic Research Program of China (2015CB250903); National Natural Science Foundation of China (51490652); Science and Technology Major Special Program for the 13th Five-Year Plan of China (2016ZX05030-005); Scientific Research Fund of China University of Petroleum in Beijing(2462016YXBS10)

引文：汪道兵，周福建，葛洪魁，等. 相互垂直裂缝应力阴影的影响因素及规律[J]. 深圳大学学报理工版，2017，34(4)：344-351.