信用风险分类预测单一模型研究及实证分析

2017-07-18邹柏松

武汉冶金管理干部学院学报 2017年2期

关键词：信用风险贝叶斯向量

邹柏松

(中南民族大学经济学院，湖北武汉 430074)

信用风险分类预测单一模型研究及实证分析

邹柏松

(中南民族大学经济学院，湖北武汉 430074)

目前，我国商业银行所面临的信用风险随着信贷业务的不断发展而逐步增加，如何对企业信用风险进行有效区分和管理，是商业银行亟待解决的问题。基于此，本文依据信用评估指标体系分别对Logistic回归模型、贝叶斯判别模型、支持向量机模型这三类模型进行了设计与构建，同时对三类模型分别进行实证分析和结果评价，从分类准确率和模型稳健性两方面对结果进行比较，作为进一步建立组合分类预测模型的基础。本文的研究成果，有利于推动我国商业银行信用风险定量度量方法的研究，从而有助于提高商业银行的风险控制水平，使得不良资产得以降低，在提高我国商业核心竞争力以及促进消费信贷市场的发展等方面有巨大的意义。

单一模型；信用风险；统计方法；数据挖掘

一、引言

近年来，我国信用风险管理水平正在逐步提升，可是随着金融业对外资银行政策的逐步开放，我国的商业银行所需面对的国际和国内竞争压力越来越大，在如今这样严峻的内外形势的考验下，为了和国际接轨，需要研究构建以计量模型为基础的信用风险管理系统，从而有效和全面地控制风险。

随着我国商业银行信贷业务的不断发展，银行将面临更大的信用风险，如何对企业信用风险进行有效区分和管理，是商业银行亟待解决的问题。尤其是我国信用风险管理体系还不够完善，关于信用风险的度量方法多是借鉴国外现有模型，针对这一情况，本文结合上市公司财务指标数据，选取目前广泛应用的Logistic回归、贝叶斯判别法等统计方法和支持向量机模型等数据挖掘方法，分别比较其实证结果的优劣。

二、基于logistic回归的信用风险分类预测模型

1.二项Logistic回归模型原理

Logistic函数，即为增长函数，在个人信用评估这一方面，Logistic回归的应用相对来说已经比较成熟，同时普遍认为在诸多统计学方法中稳健性和精确性较高，在分类问题中具有较好的特性。由于本文中输出变量只有0和1两个值，因此文中采用二项Logistic回归模型进行建模和预测，模型可以在充分借鉴一般线性回归模型的理论和思路的基础上转换而来。

首先，对于一元线性回归模型yi=β0+βixi+εi，其回归方程E(yi)=β0+βixi是对输出变量均值的预测。当输出变量为0/1二分类变量时，如果仍采用一元线性回归模型建立回归方程，则是对输入变量为xi时输出变量yi=1的概率的预测。由此给出的启示是：可利用一般线性回归模型(可以是一元，也可是多元)对输出变量取值为1的概率P进行建模，这时候，回归方程所输出的变量其取值范围为0～1，回归方程的一般形式如下所示：

(1)

在应用到实际的过程中，它们之间通常是非线性关系，一般情况下都和增长函数一致，所以应该采用非线性转换来处理概率P的转换。通过上述分析，进行的两步处理如下：

(1)把P转换为Ω

(2)

其中，Ω是指发生比或者相对风险，表示某一事件发生和不发生概率之间比值，Ω值越高，相关公司就越有可能违约，Ω值的取值范围介于0和+∞之间。

(2)把Ω转换为lnΩ

(3)

其中，lnΩ被称为LogitP。经过这个步骤的转换之后，LogitP和Ω之间依旧呈现出一致的或增长或下降的关系。

这两个步骤的转换被称为Logit变换，经过Logit变换，就能够完成在一般线性回归模型中构建输出变量以及输入变量间的多元分析模型的过程，即

(4)

称式(4)为Logistic回归方程，显然LogitP与输入变量之间是线性关系。将Ω代入，有

(5)

于是有

(6)

上式(6)是十分有代表性的增长函数，主要体现出了概率P以及输入变量它们两者的非线性关系。

Madalla就曾经选择运用Logistic模型来进行非违约和违约贷款申请人的区分，通过研究得出，在违约概率P<0.551的情况下属于非风险贷款，在违约概率P≥0.551的情况下属于风险贷款，本文中也将该判别标准应用于ST类公司和非ST类公司的判定中。

Logistic回归模型的参数估计通常采用极大似然法来计算，具体算法如下：

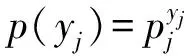
(7)

式(7)即为似然函数。对该似然函数取对数得到：

(8)

通过上式得到的βi(i=1,…,k)的估计值就是极大似然估计。通过证明得出，在样本随机时，渐进正态性、有效性和相合性等是Logistic回归模型的极大似然估计的重要特点，它一方面解决了线性回归方法之中的部分缺陷，另一方面它的实际意义也能够通过相对风险十分明显地体现出来。

2.Logistic模型实证分析

本文利用Clementine软件进行建模和预测，为避免变量之间的多重共线性，采取逐步回归的方法建立模型，对测试样本重复10次2-折交叉验证来评估模型的准确率，其基本的流程如图1、图2所示：

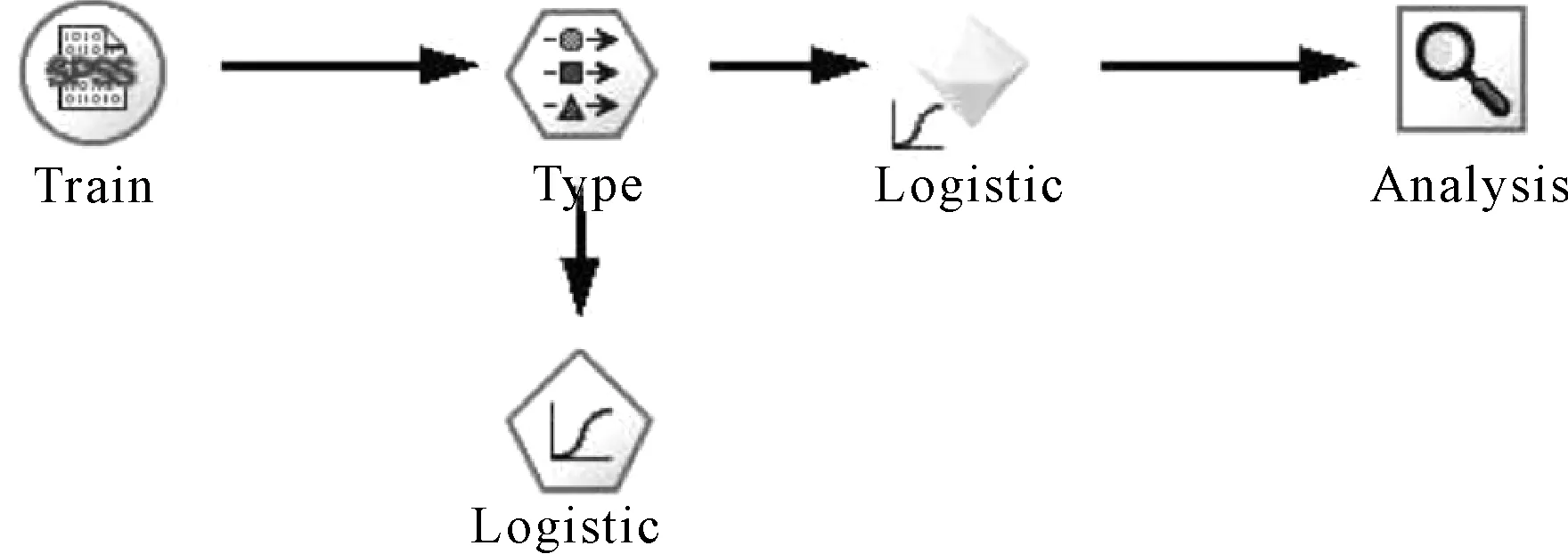
图1 Logistic训练模型图

图2 Logistic测试模型图

10次建模和预测得到的预测准确率及稳定性评估值如表1所示：

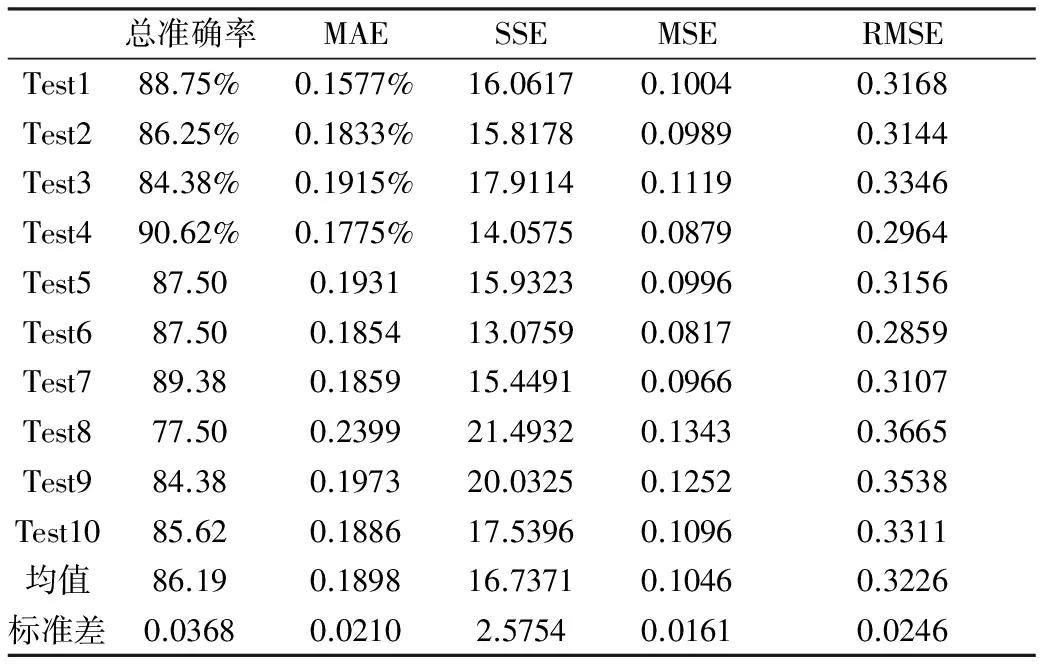
表1 Logistic模型预测结果

其模型收益(Gain)曲线图如下：

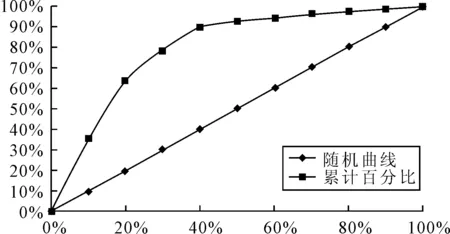
图3 Logistic训练模型图

(注：由于本文采取10次2-折交叉验证的方法，因此10次结果的平均值是用来进行Gain图绘制的数据，下同)

其中随机曲线表示在完全随机的情况下一定百分比的数据能够预测出的ST类公司的百分比，显然，这是一条45度倾斜的直线。由图3看出，大约30%的数据就可以预测出80%的ST类公司(标记值为“1”)，分类预测的效果较好。

三、基于贝叶斯(Bayes)判别的信用风险分类预测模型

1.贝叶斯(Bayes)判别的基本原理

贝叶斯判别包含于贝叶斯方法的范围之内，贝叶斯方法主要是对不确定性进行研究的一种推理方法，其中用贝叶斯概率来对不确定性进行详细的表示，而且贝叶斯概率属于一种主观概率。通常，经典概率反映的是事件的客观特征，这一概率不会随人们主观意识的变化而变化，而贝叶斯概率则不同，它是人们对事物发生概率的主观估计。

首先假设已经对研究的对象有了一定程度上的认识是贝叶斯判别法的基本思想，先验概率通常被用来对这种认识进行描述。对于多个总体的判别来说，不是考虑构建判别式，而是对待判样本属于各总体的条件概率p(l|x),l=1,2,…,k进行计算，对k个概率的大小进行比较，之后再把判定新样本来自概率最大的那一个总体。

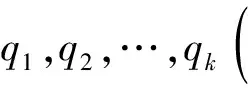
(10)

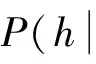
(1)训练样本的观测值

设个体分为k类，并分别从第g类中抽得ng(g=1,2,…,k)个训练样本，p个属性值，依次用x1,x2,…,xp表示，观测值如表2所示：

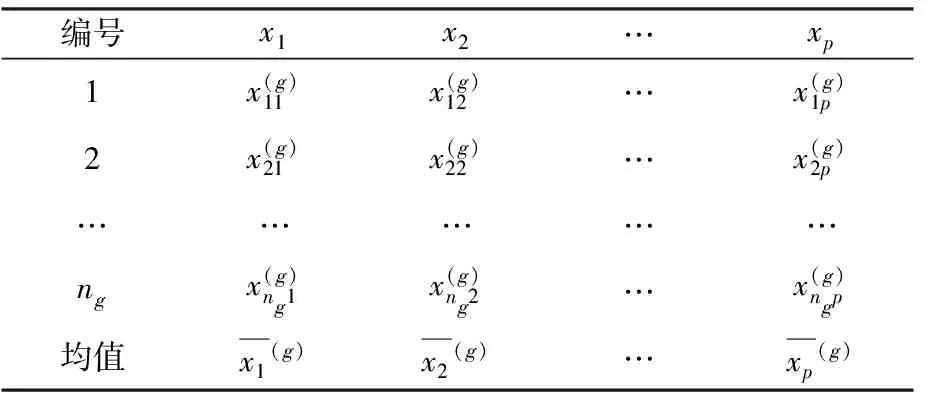
表2 g类训练样本

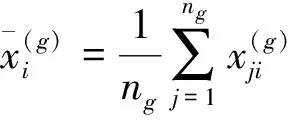
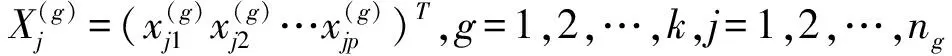
(2)建立判别函数

1)计算各类均值及协方差阵

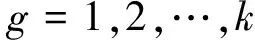
(11)

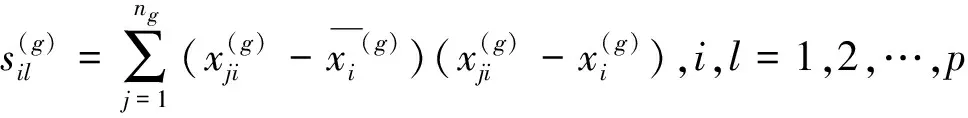
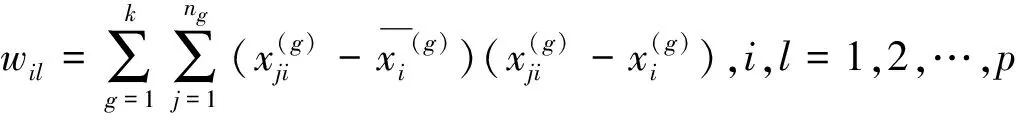
(12)

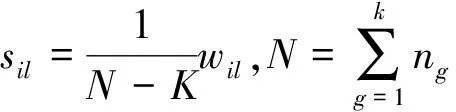
2)判别系数

计算协方差阵S的逆矩阵

令

(13)

(14)

其中

(15)

3)建立判别函数

建立判别函数如下：

(16)

对于任一样X0=(x1,x2,…,xp)，代入式(16)中，得出k个值，若其中y(g*)(X0)最大，则该个体X0=(x1,x2,…,xp)属于g*类(g*=1,2,…,k)。

2.贝叶斯(Bayes)判别模型实证分析

基于Clementine软件的贝叶斯判别模型对信用风险分类预测的基本流程如下：

图4 Bayes训练模型图

与Logistic回归模型类似，在进行分类预测时如果采用贝叶斯判别，也需要进行变量的筛选，将判别能力强的变量挑选出来构建判别函数，即逐步判别分析法,如图4。其模型收益(Gain)曲线图如图5所示：

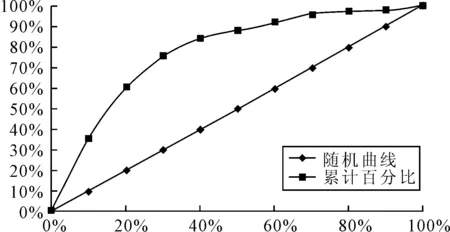
图5 贝叶斯(Bayes)判别模型收益(Gain)曲线图

由图5看出，大约30%的数据就可以预测出75%的ST类公司(标记值为“1”)，分类预测的效果较好。从总的预测准确率来看，Logistic回归模型略好于Bayes判别的结果，但Bayes判别模型的稳健性则略强于Logistic回归模型。

以上即本文采用的两种基于统计方法的分类预测模型，这两种模型均为实际应用中比较成熟的模型，相对来说，其准确率和稳健性都较好，以下将利用两种基于数据挖掘方法的模型进行分类预测。

四、基于支持向量机(SVM)的信用风险分类预测模型

1.支持向量机(SVM)的基本原理

结构风险最小化原则是支持向量机(SVM)所遵守的主要原则，该方法可以使训练及规模和VC维之间达到平衡的状态，因此有利于支持向量机在全局最优解这一目标实现的同时也实现推广能力达到最佳的目标。支持向量机(SVM)的基本思想如下，为保证推广性的置信范围以及经验风险达到最小值，同时实现对其的正确分类，从输入空间非线性将非线性可分数据集映射到相应的高维特征空间，并在该高维特征空间中对有关规划问题进行求解，同时构建出一个离超平面最近的向量和超平面之间的距离达到最大的最优分类超平面。

2.支持向量机(SVM)模型实证分析

基于Clementine软件的支持向量机模型对信用风险分类预测的基本流程如图6、图7所示：

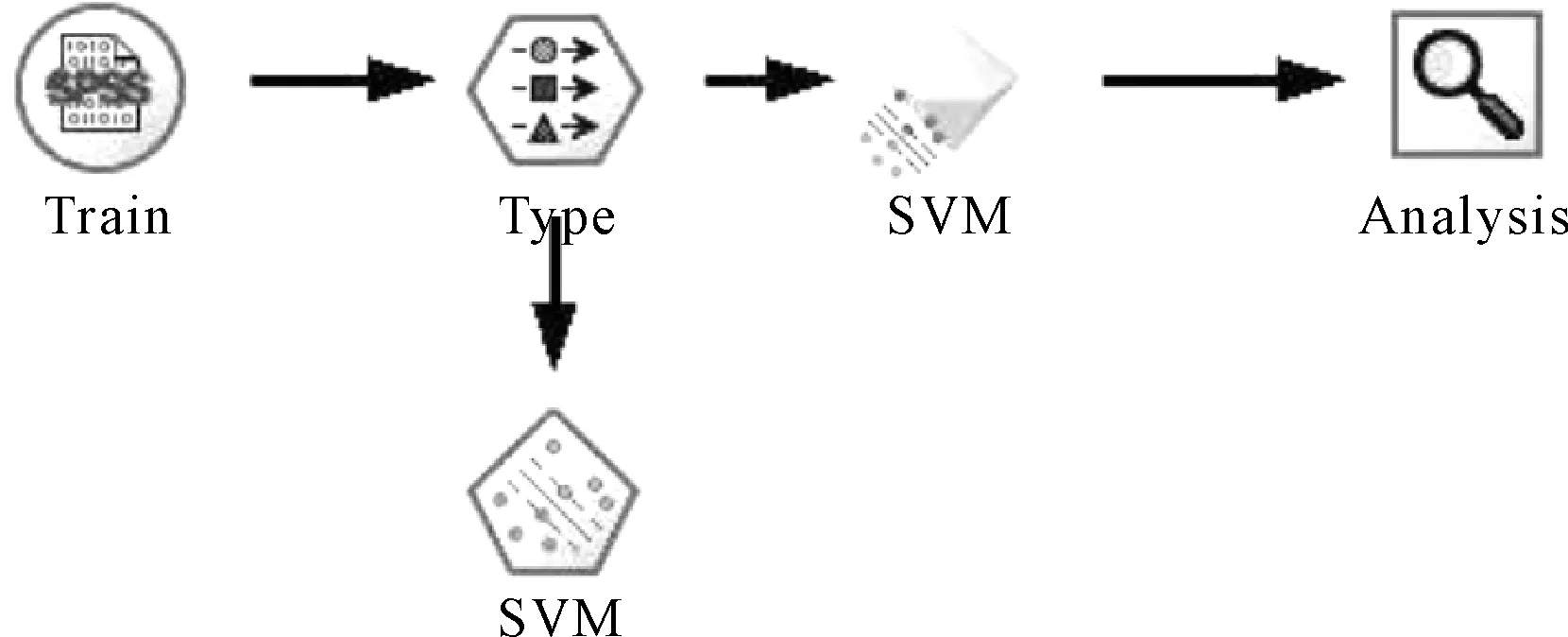
图6 支持向量机(SVM)训练模型图

图7 支持向量机(SVM)测试模型图

利用10次2-折交叉验证的方法得到的结果如表3所示：

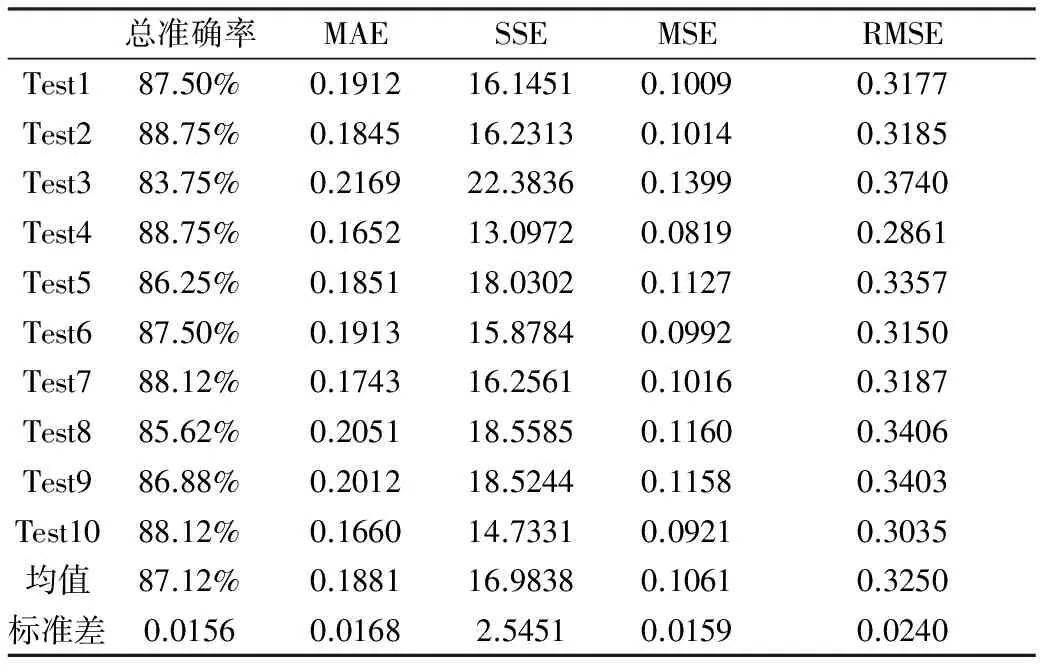
表3 支持向量机(SVM)模型分类预测结果

其模型收益(Gain)曲线图如图8所示：

图8 SVM模型收益(Gain)曲线图

通过对模型结果的研究能够看出，该模型的准确率也比较高，且30%的数据就可以预测出80%的ST类公司，说明模型效率较高。

以上两大类模型各有优劣，基于统计方法的模型优势在于模型的可解释性较好，从判别方程系数可以直观地看出财务指标的重要程度，同时，建立在统计分析基础之上的模型通常稳定性较好，其不足之处在于建模过程中对样本要求较高，样本数据的选取对模型结果的影响较大。基于数据挖掘(或机器学习)方法的模型优势在于模型在训练过程中反复进行迭代，可以达到较高的预测精度，但由于是暗箱操作，只能获得模型的最终结果而无法获知具体各变量的引用情况。

五、结论

我国股市大幅崩盘导致大量上市公司违约现象不断产生，因此使得我国商业银行所面临的信用风险越来越大，金融业面临的最为重要的风险之一即为信用风险，同时信用风险也是我国加入世贸组织之后金融市场所面临的一个重大挑战。基于此，分别利用统计模型和数据挖掘模型进行实证分析，比较各模型自身优劣，并进行实证分析和结果评价。在实际应用中，为充分利用这几类模型的优势，可以将以上几种模型进行组合，以达到更好的效果。

[1]陈秀梅,程晗.众筹融资信用风险分析及管理体系构建[J].财经问题研究,2014(12):47-51．

[2]罗方科,陈晓红.基于Logistic回归模型的个人小额贷款信用风险评估及应用[J].财经理论与实践,2017,38(1):30-35.

[3]方匡南,范新妍,马双鸽.基于网络结构Logistic模型的企业信用风险预警[J].统计研究,2016,33(4):50-55.

[4]刘祥东,王未卿.我国商业银行信用风险识别的多模型比较研究[J].经济经纬,2015,32(6):132-137.

[5]林汉川,张万军,杨柳.基于大数据的个人信用风险评估关键技术研究[J].管理现代化,2016,36(2):95-97.

[6]丁东洋,周丽莉,刘乐平.贝叶斯方法在信用风险度量中的应用研究综述[J].数理统计与管理,2013,32(1):42-56.

[7]史小康,何晓群.个人信用风险评分的贝叶斯有偏连接模型研究[J].统计与信息论坛,2015,v.30;No.173(2):3-8.

[8]邬建平.基于粗糙集和支持向量机的电子商务信用风险分类[J].数学的实践与认识,2016,46(13):87-92.

[9]隋学深,乔鹏,丁保利.基于支持向量机的贷款风险等级分类真实性审计研究[J].审计研究,2014(3):21-25.

[10]韩兆洲,林少萍,郑博儒.多类支持向量机分类技术及实证[J].统计与决策,2015(19):10-13.

责任编辑：周小梅

2017-05-28