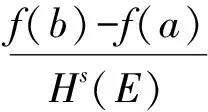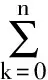分形上函数的Hs-导数
2017-07-18王司晨龙伦海
王司晨,龙伦海
(海南大学 信息科学技术学院,海南 海口 570228)
分形上函数的Hs-导数
王司晨,龙伦海
(海南大学 信息科学技术学院,海南 海口 570228)
设E是实数集R中一个要s-紧集,利用其本身的离散结构和s-维Hausdorff测度分别给出了E上实值函数的Hs-导数的定义、性质、求导法则以及导数中值定理等,对此建立了分形上一元函数的导数理论.
s-紧集; Hausdorff 测度;Hs-导数; 中值定理
一元函数的微积分是大学数学分析和高等数学课程的主要内容,具有一套完善的理论体系,其中最主要的连续、一阶导数和一重积分(包括不定积分和定积分)是建立在一维实空间即实数集R上的.是否可以在实数集R中一个小数维s-紧集[1]E上建立一元函数的微积分理论体系,文献[2-3]讨论了实数集中分形上的L-拓扑和Hs-拓扑的相关理论,文献[4]讨论了实数集中分形上函数的连续性,文献[5]研究了分形上函数的Hs-积分的基本理论.因此笔者主要讨论E上函数的Hs-导数理论,首先给出了Hs-导数的定义及性质,然后得出了Hs-导数的运算法则,最后研究了E上函数的导数的Hs-中值定理.
1 s-紧集上函数的Hs-导数的定义及性质
若F是欧氏空间上的一个有界闭集,且其s-维Hausdorff测度介于0与+∞之间,称F为一个s-紧集.设E是实数集R中的一个s-紧集,为了避免平凡性,不妨假设0 定义1 1) 如果E中的一个点满足存在该点的一个邻域(即包含该点的一个开区间)与E的交集的s-维Hausdorff测度为零,则称该点为E的一个Hs-孤立点. 2) 如果E中的一个点满足该点的任何一个右邻域都与E的交集的s-维Hausdorff测度严格大于零,且存在该点的一个左邻域与E的交集的s-维Hausdorff测度为零,则称该点为E的一个Hs-右内端点;同样可定义E的Hs-左内端点. 3) 如果E中的一个点满足该点的任何一个邻域都与E的交集的s-维Hausdorff测度严格大于零,则称该点是E的一个Hs-内点. 根据E中点的分类的定义1,当x0是E的Hs-内点时,J(x0)只包含x0;当x0是E中的Hs-左内端点时,x0是J(x0)中的最小点;当x0是E中的Hs-右内端点时,x0是J(x0)中的最大点;当x0既是E的左端点又是E的Hs-右内端点时或者既是E的右端点又是E的Hs-左内端点时,J(x0)只包含x0;当x0既是E的左端点又是E的Hs-孤立点时,x0一定是J(x0)中的最小点,其最大点一定是E中的Hs-右内端点;同样当x0既是E的右端点又是E的Hs-孤立点时,x0一定是J(x0)中的最大点,其最小点一定是E中的Hs-左内端点.因此当x0不是E的Hs-内点时,J(x0)的最大点和最小点中至少有一个是内端点,其他点一定是E中的Hs-孤立点. 设f(x)是s-紧集E上的一个以x为自变量的一元实函数,给出f(x)在E上的Hs-连续的定义. 根据定义2中E上的所有L-连续函数的四则运算和复合运算保持Hs-连续性不变,所有Hs-连续函数一定在E上具有有界性、最值性、介值性和一致连续性等很好的性质,即E上的Hs-连续函数的值域为一闭区间. 给出E上函数f(x)的Hs-导数的定义. 1) 当x0是E的Hs-左内端点时,若极限 2) 当x0是E的Hs-右内端点时,若极限 3) 当x0是E的Hs-内点时,若函数f(x)在x0处的Hs-左导数和Hs-右导数都存在且相等,则称函数f(x)在x0处的Hs-导数存在,称该共同的极限值为f(x)在x0处的Hs-导数,记为f(1,s)(x0). 几何解释:从定义3可以看出,当x0是E的Hs-内点时,由于自变量x在E内从x0的左边变化到右边的过程中,x与x0为端点的闭区间与E的交集的s-维Hausdorff测度严格大于零,且x越接近x0,该Hausdorff测度值越接近于零,对此便可以将该Hausdorff测度值来代替通常的一元函数的导数的定义中的x与x0之间的长度,来得到f(x)在x0处Hs-导数的定义,因此Hs-导数值f(1,s)(x0)表示函数f(x)在x0处的函数值的改变量随自变量x在E中的Hausdorff测度的改变量的瞬时变化率. 给出E上的函数f(x)在E中除了Hs-内点之外的其他点的Hs-可导性和Hs-导数的定义. 1) 当x1和x2中只有一个是E的Hs-内端点时,若f(x)在J(x0)上是常函数,并且f(x)在x1和x2中的内端点处的单侧Hs-导数存在,则称f(x)在x0处是Hs-可导的,其Hs-导数值f(1,s)(x0)定义为f(x)在x1和x2中的内端点处的单侧Hs-导数值. 由定义4可知,如果x0不是E的Hs-内点且J(x0)包含不止一个点的情况下,当f(x)在x0处Hs-可导时,f(x)在J(x0)中的每一点均Hs-可导,且Hs-导数值都等于f(1,s)(x0). 定义5 设f(x)是E上的实函数. 1) 若函数f(x)在E中的每一点处都是Hs-可导的,则称f(x)在E上Hs-可导,其Hs-导函数记为f(1,s)(x)或者(f(x))(1,s),当f(1,s)(x)是E上是Hs-连续函数时,则称f(x)在E上是Hs-连续可导的. 2) 如果f(x)在E上Hs-导函数f(1,s)(x)继续是Hs-可导的,则称f(x)在E上的二阶Hs-导函数存在,用f(2,s)(x)表示,同样用f(n,s)(x)表示f(x)在E上的n阶Hs-导函数. 定理1 若函数f(x)在E上是Hs-可导的,则f(x)是E上是Hs-连续函数,即Hs-连续是Hs-可导的必要条件. 例1 E上的常函数f(x)是Hs-可导的,并且f(1,s)(x)=0. 由函数的Hs-导数的定义和实数集上一元函数的求导法则,不难得到如下的四则运算求导公式. 设f(x)和g(x)是E上的2个Hs-可导函数,有 (f(x)±g(x))(1,s)=f(1,s)(x)±g(1,s)(x), (f(x)g(x))(1,s)=f(1,s)(x)g(x)+f(x)g(1,s)(x), 定理2 设u=f(x)是Hs-可导函数,g(u)是f(x)的值域(闭区间)上的一个一阶连续可导的函数,有 ((g°f)(x))(1,s)=g′(f(x))·f(1,s)(x) . g(f(x2))-g(f(x1))=g′(ξ)(f(x2)-f(x1)), 其中,ξ介于f(x1)和f(x2)之间, 对等式取x2-x1→0就可得到定理2的结论. 证毕. 定理3 设u=f(x)是Hs-连续可导函数,其值域为[c,d],则唯一存在一个从[0,Hs(E)]到[c,d]上的一阶连续可导可逆函数g(u),使得f(x)=(g°h)(x),其中h(x)=Hs(E∩[a,x])为例2中恒等函数在测度空间(E,Hs)上的一个分布函数,a为E的最小点. ((g°h)(x))(1,s)=g′(u)h(1,s)(x)=g′(u) . 证毕. 利用定理3和复合函数的Hs-求导法则,就有E上函数的Hs-导数的计算公式 f(1,s)(x)=g′(h(x)) . 由于Hs-导数的罗尔定理是拉格朗日定理的特殊情况,因此只给出Hs-导数的拉格朗日中值、柯西中值和泰勒公式. 定理4 设a,b是s-紧集E的最小和最大值点,u=f(x)是Hs-连续可导函数, 证明 由定理3可知,存在从E到[0,Hs(E)]上的Hs-连续可导函数h(x)和一个从[0,Hs(E)]到f(E)上的一阶连续可导可逆函数g(u),使得f(x)=(g°h)(x).由于 因此只需对g(u)在闭区间[0,Hs(E)]上使用拉格朗日中值定理和复合函数的Hs-导数的求导法则即可得到定理4的证明. 证毕. f(x0+Δx)=f(x0)+f(1,s)(ξ)h(x0+Δx) . 另外可由定理4得出以下推论 推论1 1)E上的Hs-连续可导函数f(x)的Hs-导函数f(1,s)(s)≡0的充分必要条件是f(x)为常函数. 2)E上的满足f(1,s)(s)≡g(1,s)(x)任意2个Hs-连续可导函数f(x)和g(x)之间只相差一个常数. 定理5 设a,b是s-紧集E的最小和最大值点,f(x)和g(x)都是Hs-连续可导函数,且g(1,s)(x)在E内无零点, 证明 构造辅助函数 f(x)=(f(b)-f(a))g(x)-(g(b)-g(a))f(x), 可验证得f(a)=f(b),因此只需对f(x)使用定理4便可得到定理5的证明. 证毕. 则在E中存在严格介于x0和x0+Δx之间的点ξ使得等式成立,其中,R(Δx)=f(n+1,s)(ξ)hn+1(Δx)和对任意0≤k≤n+1, 证明 作辅助函数 然后对函数重复使用n+1次定理5的结论即可证明定理6. 证毕. [1]FalconerKJ.FractalGeometry:MathematicalFoundationsandapplications[M].Chichester:JohnWilley&Sons, 2003. [2] 龙伦海,梁莉,单家俊. 直线上子集的Hs-拓扑及其应用[J/OL]. 数学杂志,2017,37(2):401-408. [3] 龙伦海,何勇,梁莉. 分形上的拓扑及其性质[J]. 海南大学学报:自然科学版,2014,32(2):102-110. [4] 梁莉,龙伦海,何勇. 实数集中分形上函数的连续性[J]. 海南大学学报:自然科学版,2015,33(2):15-19. [5] 朱莉红. 分形上函数的积分[D]. 海口:海南大学,2014. Hs-derivative of Function on Fractal Wang Sichen, Long Lunhai (College of Information Science and Technology, Hainan University, Haikou 570228, China) In the report, ifEis as-compact set in the real number set, the discrete structure ands-Hausdorff measure were used to obtain the definition, property, derivation method and derivative of the mean value theorem of theHs-derivative on the real function inE, and a function on fractal geometry derivative theory was established. compacts-set; Hausdorff measure;Hs-derivative; the mean value theorem 2017-01-16 海南省自然科学基金 (113003) 王司晨(1993-),女,安徽天长人,海南大学 2014 级研究生,研究方向:分形几何,E-mail:18789266226@163.com 龙伦海(1965-),男,重庆大足人,教授,博士,研究方向:分形几何,E-mail:13118900189@163.com 1004-1729(2017)02-0095-05 O 174.12 A DOl:10.15886/j.cnki.hdxbzkb.2017.0017



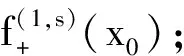


2 s-紧集上函数的Hs-导数的运算法则

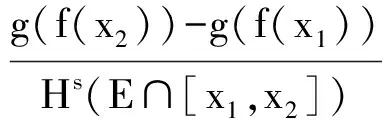
3 s-紧集上函数的Hs-导数的中值定理