相互贯通裂纹动态断裂的试验研究
2017-07-18杨仁树张渊通
杨仁树, 苏 洪, 陈 程, 龚 悦, 张渊通
(1.中国矿业大学(北京) 力学与建筑工程学院,北京 100083; 2.安徽理工大学 土木学院,安徽 淮南 232001)
相互贯通裂纹动态断裂的试验研究
杨仁树1, 苏 洪1, 陈 程1, 龚 悦2, 张渊通1
(1.中国矿业大学(北京) 力学与建筑工程学院,北京 100083; 2.安徽理工大学 土木学院,安徽 淮南 232001)

动荷载;动焦散;相互贯通裂纹;动态应力强度因子
动荷载下含缺陷介质岩石断裂行为与静载作用下的岩石断裂行为差异很大,与静态时相比,动态断裂行为更加复杂,因此,动态断裂力学一直是学者们关心的热点问题,同时也是难点问题[1-2]。实际工程中,岩石中不仅含有大量裂纹,这些裂纹还会贯通,在爆破、地震、扰动等动荷载作用之下失稳断裂,严重影响工程质量。所以动荷载作用下含相互贯通裂纹的岩石断裂行为研究,不仅具有重要科学意义,而且在工程结构的安全评价等方面具有广泛的工程应用背景。
动态焦散线方法是研究动态断裂力学问题重要的实验方法。Kalthoff[3]采用焦散线方法研究了动荷载和静荷载作用下裂纹传播的两类问题,并推导出动态应力强度因子计算公式。Kawagishi等[4-5]分别研究了不同切开尺寸裂纹和不同倾斜角度裂纹尖端的动态断裂效应。Kalthoff等[6-7]等利用光测力学实验手段,研究了含预制裂纹梁结构的动态断裂机理和动态断裂韧性等参数变化规律。姚学锋等[8]借助高速相机和光测力学等研究手段,分析了含有预制缺陷介质的试件在动荷载作用下能量释放率与裂纹扩展速度、时间等参数关系。贾敬辉等[9]利用RFPA2D-Dynamic数值分析软件模拟了含预制偏置裂纹的三点弯曲梁由I型断裂转化为II型断裂时的裂纹偏置位置变化规律。宋义敏等[10]利用自制落锤冲击加载试验机,采用数字散斑实验方法,研究了5组不同预制裂纹长度的花岗岩试件在冲击荷载作用下动态断裂行为。Fender等[11]研究了在动荷载作用下两条相向运动裂纹扩展行为。
以上学者利用各种方法分析了动荷载下单支裂纹的断裂行为,然而研究贯通裂纹之间的相互作用较少。本文结合动焦散实验系统对类岩石材料[12]在冲击荷载作用下相互贯通裂纹的起裂、扩展等规律进行研究,这些研究可为工程实践提供帮助。
1 动焦散试验系统及原理
1.1 焦散线原理及系统
焦散线方法最早由Manogg[13]提出,其实验原理如图1所示,实验系统如图2所示。试件在未受荷载作用时其厚度是均匀的,当受荷载时厚度发生改变,其奇异点附近区域的厚度将会变得不均匀,厚度和折射率都会发生变化,激光器发出的点光源经过场镜a后会变成平行光,当平行光垂直入射到该受载模型时,模型前后表面射出的反射光线和折射光线都将偏离平行状态,偏离平行状态的光线会在传播路径上形成如图1所示的光强分布不均的图像,阴影区称为焦散斑。偏离平行状态的光线经过场镜b后在其焦距处的高速相机中成像,最后传输到计算机中。

图1 焦散线成像示意图
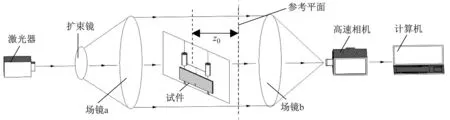
图2 动焦散实验系统示意图
1.2 裂纹动态应力强度因子
倾斜裂纹[14]在冲击荷载作用下断裂属于I、II型复合断裂,因此裂纹尖端动态应力强度因子采用Theocaris等[15]提出的方法计算,计算式如式(1)、式(2)所示。
(1)
(2)

2 实验描述
试件选用类岩石材料PMMA板,动态力学参数为:Ed=4.5GN/m2,Cp=2.32km/s,Cs=1.26km/s,υd=0.31,|Ct|=0.88×10-10m2/N。材料规格为220mm×50mm×5mm,三条预制裂纹相交于试件下部,如图3所示。A、B、C三支裂纹长度为5mm,裂纹C与竖直方向夹角θC为45°,只改变裂纹B与竖直方向夹角θB为15°、30°、60°、75°,依次记为模型a~模型d。

图3 实验模型示意图
试验采用自由落锤对试件进行冲击加载,冲击加载装置如图4所示,落锤质量为2kg,落锤高度为360mm。
3 试验结果及分析
3.1 试验结果
图5为动荷载作用下不同模型断裂图,图6为模型部分动态焦散图。当落锤冲击试件后,相互贯通的两分支裂纹B和裂纹C只有一端起裂扩展,当分支裂纹B角度θB=15°、30°时,翼裂纹从分支裂纹B尖端起裂;当分支裂纹B角度θB=60°和75°时,翼裂纹从分支裂纹C尖端起裂。模型a~模型d起裂端的分支裂纹与竖直方向夹角θ分别为15°、30°、45°、45°。翼裂纹起裂以后先沿准竖直方向扩展一段距离,裂纹断面较为光滑,此阶段称为阶段1,当裂纹扩展到试件约2/3高度时,裂纹扩展轨迹弯曲程度加大,曲裂现象明显,此阶段称为阶段2。
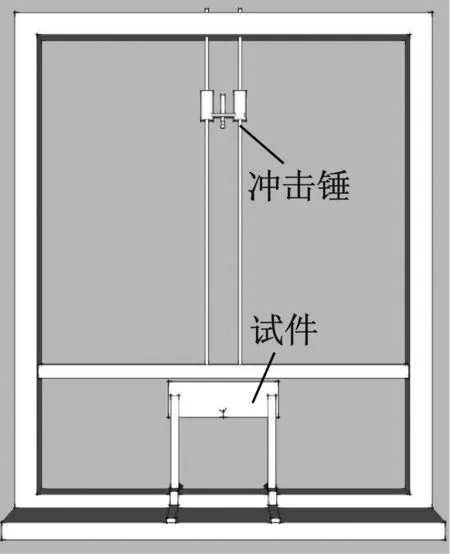
图4 加载装置示意图

(a) 模型a(θB=15°)

(b) 模型b(θB=30°)

(c) 模型c(θB=60°)

(d) 模型d(θB=75°)

50 μs

130 μs

220 μs

290 μs

70 μs

150 μs

220 μs

310 μs

70 μs

130 μs

200 μs

270 μs

70 μs

150 μs

200 μs

280 μs
3.2 翼裂纹扩展轨迹分析
图7为翼裂纹扩展时偏转角度随位移变化图。翼裂纹偏转角为翼裂纹扩展过程中偏离竖直方向角度,规定偏向冲击点方向为正,背离冲击点方向为负。由图7可以看出,所有模型翼裂纹偏转角首先从负角度开始,然后在0°附近振荡变化,即沿准竖直方向扩展。当翼裂纹扩展至试件约2/3高度时,翼裂纹偏转角度随位移变化曲线振幅明显加大,波动剧烈,说明翼裂纹曲裂程度加剧。模型a~模型d最大偏转角度(绝对值)分别为8°、11.6°、17.7°、18°,结合图5可以看出随着起裂端的分支裂纹与竖直方向夹角θ的增大,翼裂纹在第二阶段偏离竖直方向的程度越大,扩展轨迹弯曲程度增大。对比分析模型c和模型d,发现两模型翼裂纹扩展轨迹几乎一致,说明两相互贯通的裂纹中未起裂的分支裂纹角度变化对起裂的分支裂纹扩展轨迹几乎没有影响。

图7 翼裂纹偏转角随裂纹扩展位移变化图
基于以上规律,在实际工程中可预测相互贯通裂纹扩展轨迹,为防止断裂事故发生,可在预测的裂纹扩展轨迹附近加强试件或设置障碍使裂纹难以扩展,起到防止断裂事故发生的作用。
3.3 翼裂纹扩展速度分析
图8为翼裂纹扩展速度随时间变化曲线。由图8可知,翼裂纹起裂后速度迅速升高,在扩展第一阶段,速度在小范围振荡变化,当裂纹扩展至第二阶段时,扩展速度有较明显下降趋势,这主要是因为,裂纹在第一阶段内扩展,裂纹曲裂程度较弱,基本沿竖直方向扩展,能量消耗较小,所以扩展速度维持在小范围变化,当裂纹扩展到第二阶段时,裂纹曲裂程度明显加强,能量消耗加剧,所以裂纹扩展速度迅速下降。模型a~模型d裂纹扩展速度的平均值分别为141.79 m/s、138.56 m/s、125.09 m/s、125.67 m/s。由此可见翼裂纹平均速度随着起裂端的分支裂纹与竖直方向夹角θ的增大而减小。试验中每次落锤质量和落锤高度一样,试件内存储的应变能基本相同,但由于随着夹角θ增大,裂纹曲裂程度加大,能量耗散增加,所以裂纹扩展平均速度会降低。

(a) 模型a(θB=15°)
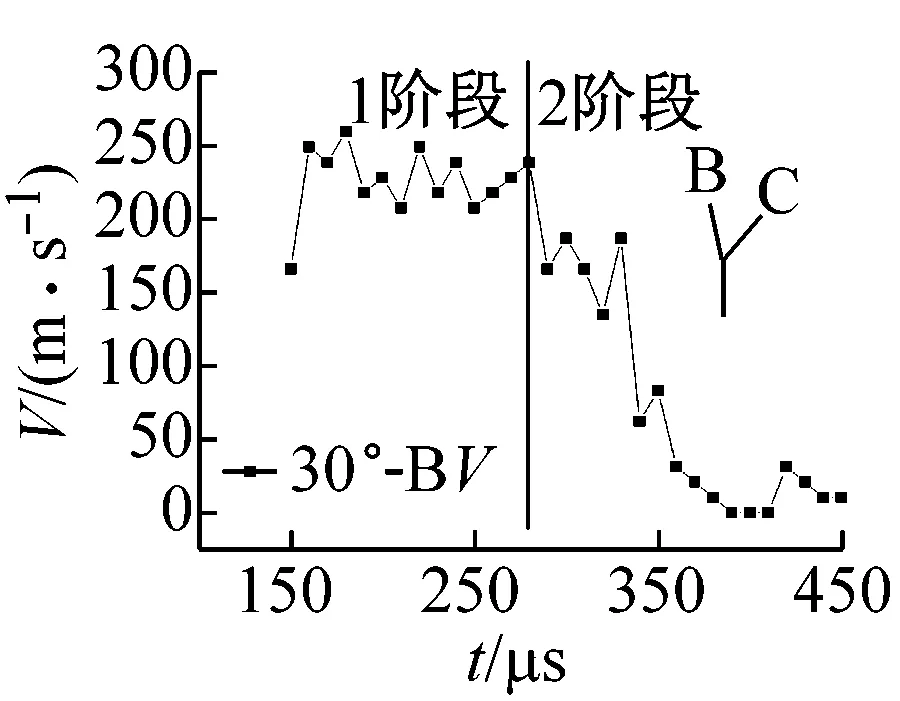
(b) 模型b(θB=30°)
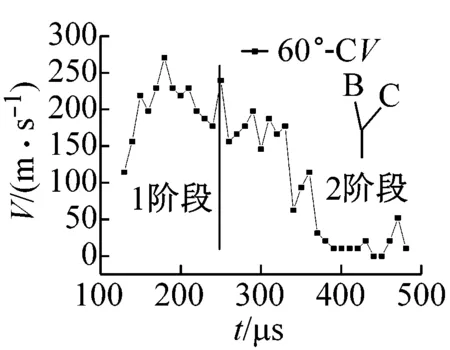
(c) 模型c(θB=60°)
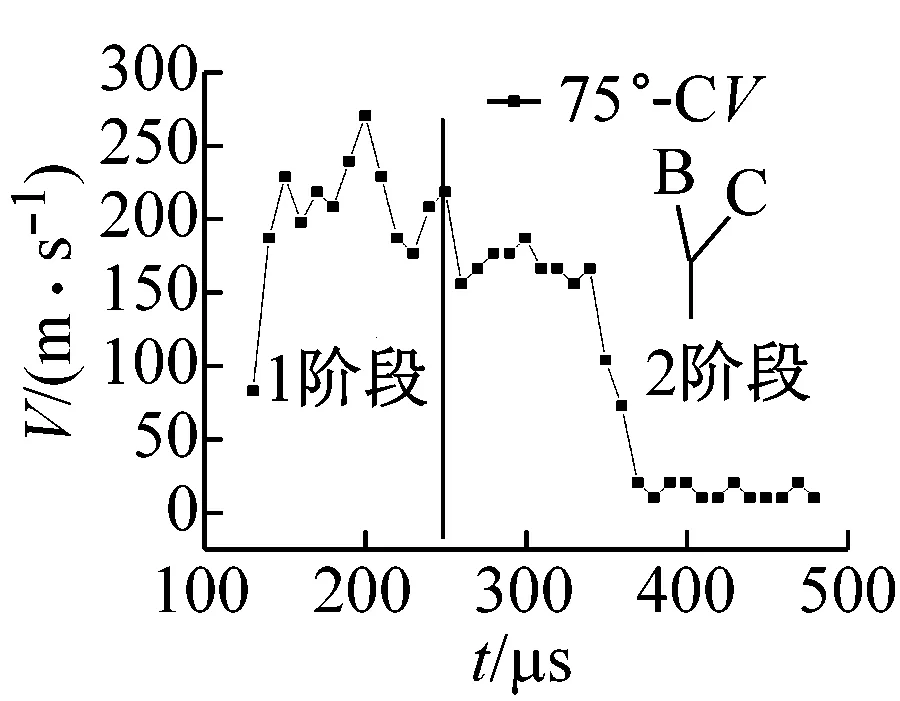
(d) 模型d(θB=75°)
3.4 动态应力强度因子分析
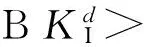
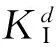

(a) 模型a(θB=15°)

(b) 模型b(θB=30°)
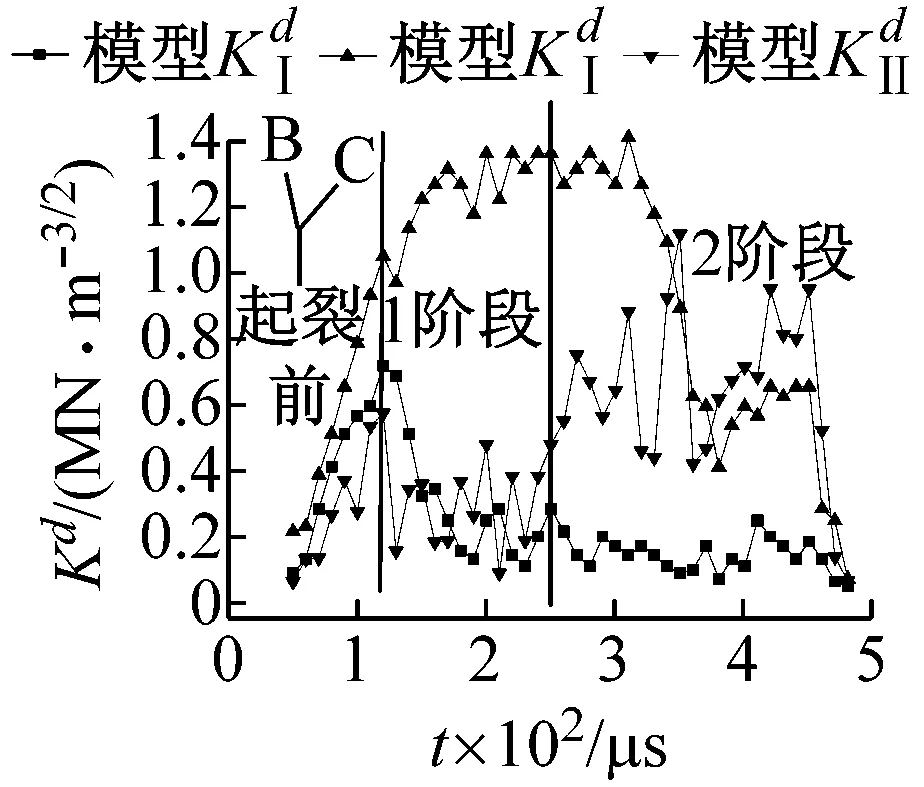
(c) 模型c(θB =60°)

(d) 模型d(θB=75°)
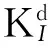

图10 分支裂纹起裂瞬间Kd与夹角θ的变化曲线
Fig.10Relationshipbetweendynamicstressintensityfactoratthebranchcrackinitiationmomentandangle
4 结 论
(1) 两分支裂纹相互贯通,在动荷载作用下翼裂纹只会从与竖直方向夹角较小分支裂纹尖端起裂扩展,当有一支分支裂纹起裂后,另一分支裂纹动态应力强度因子快速下降,试件内应变能重新分布。
(2) 翼裂纹起裂后首先沿准竖直方向扩展,翼裂纹曲裂程度不大,当翼裂纹扩展至试件约2/3高度时,裂纹曲裂程度增大,I-II复合型断裂现象明显加强。
(3) 翼裂纹起裂后,速度快速上升,当扩展至第二阶段后,速度下降,并且翼裂纹平均速度随着起裂端分支裂纹与竖直方向夹角θ的增大而减小。
[1] 任利,谢和平,谢凌志,等. 基于断裂力学的裂隙岩体强度分析初探[J]. 工程力学,2012, 30(2): 156-162.
RENLi,XIEHeping,XIELingzhi,etal.Preliminarystudyonstrengthofcrackedrockspecimenbasedonfracturemechanics[J].EngineeringMechanics, 2012, 30(2): 156-162.
[2]LEEPY,SUNZC,LIAOM,etal.ThestudyofcrackmechanismduringarcbrazingofcoolingpipetoITERmagnetsupportsystem[J].IEEETransactionsonAppliedSuperconductivity, 2014, 24(3): 1-14.
[3]KALTHOFFJF.Shadowopticalmethodofcaustics[M]. 2nded.[S.l.]:VCHPublishersInc., 1993: 407-476.
[4]KAWAGISHIY,SHOZUM,HIROSEY.Experimentalevaluationofstressfieldaroundcracktipbycausticmethod[J].MechanicsofMaterials, 2001, 33(12): 741-757.
[5] 杨仁树,王雁冰,候丽冬,等. 冲击荷载下缺陷介质裂纹扩展的DLDC试验[J]. 岩石力学与工程学报,2014, 33(10): 1971-1976.
YANGRenshu,WANGYanbing,HOULidong,etal.DLDCexperimentoncrackpropagationindefectivemediumunderimpactloading[J].ChineseJournalofRockMechanicsandEngineering, 2014, 33(10): 1971-1976.
[6]KALTHOFFJF.Onthemeasurementofdynamicfracturetoughness-areviewofrecentwork[J].InternationalofFracture, 1985, 27(3): 277-298.
[7]THEOCARISPS,ANDRIANOPOULOUSNP.Dynamicthree-point-bendingofshortbeamsstudiedbycaustic[J].InternationalJournalofSolids&Structures, 1977, 17(7): 707-715.
[8] 姚学锋,方竞. 冲击荷载下扩展裂纹尖端动态能量释放率分布的焦散线分析[J]. 爆炸与冲击,1996, 16(2): 111-116.
YAOXuefeng,FANGJing.Analysisofcausticsondynamicenergyreleaserateofrunningcracktipunderimpactload[J].ExplosionandShockWaves, 1996, 16(2): 111-116.
[9] 贾敬辉,张永彬. 动荷载作用下三点弯曲梁的破坏形式与偏置裂纹位置的关系[J]. 武汉理工大学学报,2012, 34(11): 84-87.
JIAJinghui,ZHANGYongbin.Relationsbetweenthelocationofthenotchandthefailuremodeinthree-pointbendingbeamunderthedynamicloads[J].JournalofWuhanUniversityofTechnology, 2012, 34(11): 84-87.
[10] 宋义敏,何爱军,王泽军,等. 冲击荷载作用下岩石动态断裂试验研究[J]. 岩土力学,2015, 36(4): 965-970.
SONGYimin,HEAijun,WANGZejun,etal.Experimentstudyofthedynamicfracturesofrockunderimpactloading[J].RockandSoilMechanics, 2015, 36(4): 965-970.
[11]FENDERML,LECHENAULTF,DANIELSKE.Universalshapesformedbytwointeractingcracks[J].PhysicalReviewLetters, 2010, 105(12): 1-4.
[12]ROSSMANITHHP,DAEHNKEA,KNASMILLNERREK,etal.Fracturemechanicsapplicationstodrillingandblasting[J].FatigueandFractureEngineeringMaterialsandStructures, 1997, 20(11): 1617-1636.
[13]MANOGGP.Anwendungderschattenoptikzuruntersuchungdeszerreissvorgangsvonplaten[D].WestGermany:UniversityofFreiburg, 1964.
[14] 李清,郭洋,马万权,等. 半圆盘构件冲击断裂特性的动态焦散线实验研究[J]. 振动与冲击,2016, 35(9): 52-58.
LIQing,GUOYang,MAWanquan,etal.Dynamiccausticstestsforsemi-circularspecimenunderimpactloading[J].JournalofVibrationandShock, 2016, 35(9): 52-58.
[15]THEOCARISPS,GDOUTOSEE.ThemodifiedDugdale-Barenblattmodeladaptedtovariousfractureconfigurationsinmetals[J].InternationalJournalofFracture, 1974, 10(4): 549-564.
Tests for dynamic fracture of interconnected cracks
YANG Renshu1, SU Hong1, CHEN Cheng1, GONG Yue2, ZHANG Yuantong1
(1. School of Mechanics and Civil Engineering, China University of Ming and Technology, Beijing 100083, China;2. School of Civil Engineering, Anhui University of Science and Technology, Huainan 232001, China)
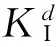
dynamic load; dynamic caustics; interconnected crack; dynamic stress intensity factor
国家自然科学基金面上项目(51274203;51374210);国家重点研发计划(2016YFC0600903);高等学校学科创新引智计划资助(B14006)
2016-08-02 修改稿收到日期:2016-10-23
杨仁树 男,博士,教授,1963年生
苏洪 男,博士,1987年生 E-mail:suhonggy2016@163.com
TD2
A
10.13465/j.cnki.jvs.2017.13.021
