先练后讲 精彩不断

朱丽桃

传统的教学模式大都是以传授知识为特征，表现在数学学科上是先讲后练。这种教师的先讲，必然会限制学生的思维，学生在模仿中难有创新的机会。邱学华教授创立的尝试教学理论以学生的尝试为核心，坚持先练后讲、先试后导，学生的思维由于没有受到限制，可以这样试，也可以那样试，始終处于自由发散状态，为创新留下了空间，在课堂上容易产生让人意想不到的创新火花。对此，许多教师担心：教师先不讲，学生尤其是潜能生能通过尝试获得成功吗？我的实践经验是：尝试能否成功，关键在于教师在尝试铺垫时对新知的切入点的选择是否得当。以下是笔者的具体操作实例。

如，教学按比分配应用题时，课本例题是：一筐苹果有240个，甲班有30人，乙班有20人，按两个班的人数比来分配，两个班各应分得多少个？在尝试解答例题前，可给学生安排两个层次的尝试准备题：1.一个班男生与女生的人数比是5∶3，是把全班的人数当成（）份，男生占（）份，女生占（）份，也说明男生占全班的（），女生占全班的（）。2.李阿姨买回240个苹果，现平均分给两个班，每班可分得多少个？接着出示例题让学生尝试解答，先启发学生：这种情况下，还能平均分吗？应该怎样分？再放手让学生尝试解决。由于有了解答准备题的经验，学生不但能解决尝试题，还出现了多种解决问题的策略。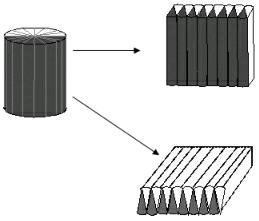

再如，教学圆柱体积这一内容后，教师出示练习题：一个圆柱的侧面积是94.2平方厘米，它的底面半径是3厘米，求圆柱的体积是多少？如果教师先行提示，学生一般会采用这样的思路：先用侧面积÷底面周长求出高，即：37.68÷（2×3.14×3）=5（厘米），再用圆柱的体积公式可得：3.14×32×5=141.3（立方厘米）。而我在教学时，让学生先行尝试，学生中出现了这样的创新想法：94.2÷2×3=141.3（立方厘米）。这是什么意思？说实话，当时我也没有想清楚，于是进行了这样的处理：“这个我真不懂，你能够把你的想法说给大家听听吗？”只见该生不慌不忙地向我讨要了一个研究圆柱体积的切拼教具，请求我协助他完成圆柱的切拼。（如图所示）拼好后，他得意地解释说：“其实只要将切拼后的长方体由竖放改成横放，用侧面积÷2得到的是长方体的底面积，此时圆柱的半径相当于长方体的高。侧面积94.2÷2×3就得到长方体的体积，而长方体的体积就是圆柱体的体积。”多好的解题思路，多灵动的思维，我想：这既是尝试教学“先试后导”带来的惊喜，更是对我多年来坚持直观教学的一种肯定。

（作者单位：娄底市第八小学）