让数学学习有深度

雷金贵

勾股定理教学片段

一、创设情境，激发兴趣

师：观察下列图片，它们都与什么图形有关？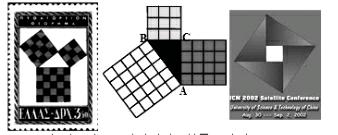

生：（齐答）直角三角形，正方形！

师：这3幅图分别是一张希腊为纪念一个重要数学定理而发行的邮票、华罗庚教授建议向外太空发射与外星人联系的图案、2002年国际数学家大会会标———弦图。它们都可以证明一个重要定理。大家想知道是哪个定理吗？（生：想！）下面老师和大家一起来探索这个定理！

二、用数学的眼光看问题

师：相传两千多年前，古希腊著名的哲学家、數学家毕达哥拉斯去朋友家做客时看着朋友家的方砖地发起呆来。原来，朋友家的地是用一块块直角三角形形状的砖铺成的，黑白相间，非常美观大方（如图所示）。请你也来观察一下，看能发现些什么。

师：原来毕达哥拉斯发现了地砖上的3个正方形存在某种关系，你发现了吗？

探究活动1：你能找出图中3个正方形面积之间的关系吗？请说说理由。

生2：如果一个小的等腰直角三角形的面积为1，那么两个小正方形的面积之和与大正方形的面积都等于4。

三、深入探究，交流归纳

探究活动2：问题1：设每个小正方形的面积为1，分别计算下列图形中（图略）正方形A、B、C的面积，它们之间都有上述关系吗？

问题2：你能用等腰直角三角形的边长表示正方形的面积吗？由此猜想等腰直角三角形三边有怎样的关系？

生4：我发现每个正方形的面积都等于直角三角形边长的平方：若一个等腰直角三角形的两条直角边为a，斜边为c，则有a2+b2=c2。

反思

以上案例，几乎是目前勾股定理教学的蓝本，老师们大都这样设计。然而，仔细思考的话，我们会发现，这样的探究教学是没有深度的，也就是我们常说的探究流于形式。

为什么这样说呢？勾股定理是一个基本的几何定理。定理的发现和证明都是众多前人智慧的结晶（注意，不是一两个人突然发现的）。仅凭老师提供的几个图案，以及初中生现有的数学素养，要想在课堂40分钟内发现这个重要的几何定理，其难度可想而知。于是，基于勾股定理的探究教学就显得滑稽可笑了。对于勾股定理这样的内容的教学，我们应重在引导学生理解其含义。

接受学习和发现学习都是数学学习的重要方式。一般来讲，简单的数学概念、法则、结论等学生能够去发现的，可以采用发现学习；陈述性的、事实性的知识，或者是教学的疑难点、易错点，则应该采用接受学习。这样一来，我们的教学才不会偏离方向。有老师认为，在接受学习中，学生可能被动地学习，而在发现学习中，学生更能够主动学习。其实，设计得好的接受学习同样能有效地激发学生学习的主动性，使学习更有深度。相反，如果在发现学习中创设的问题情境、提出的问题、活动的组织等不恰当的话，也可能导致学生被动地学习。

（作者单位：津市市白衣镇中学）