图形与几何教学策略探析

张丁钗（永泰县嵩口中心小学，福建永泰350700）

图形与几何教学策略探析

张丁钗
（永泰县嵩口中心小学，福建永泰350700）

“图形与几何”的教学重在激发学生的空间想象力和创造力，为此，教师要善于引导学生经历图形抽象的过程，体会数学源于生活，理解数学的思维方式与原理；经历分类与辨析的过程，感悟数学思想方法；经历探索与发现的过程，累积数学活动经验；经历图形的转化过程，发展学生空间观念。

空间想象力；创造力；图形与几何；教学策略

《全日制义务教育数学课程标准（2011年）》在总体目标中明确提出“四基”，即基础知识、基本技能、基本思想、基本活动经验。那么，在学习“图形与几何”过程中，除了要把握图形的特征与性质以外，在基本思想与基本活动经验方面，有怎样的要求呢？《标准》较多地使用“观察、操作、认识、经历……”“结合实例（生活情境）了解……”“通过实物和具体模型，了解……”的表述，这实际上明确了认识图形的过程和方式为观察、操作、探索等。同时，《标准》中较多地使用了“经历、体验”等过程性目标动词，这也说明学生对图形的认识以及图形特征的把握不是一蹴而就的，数学需要凸显认识图形的过程性和体验性，而抽象、分类、探索、转化等是其中很重要的环节。

一、经历图形抽象的过程，体会数学源于生活

图形本身不是客观存在的具体东西，是抽象的结果，在抽象过程中抛弃了物体颜色、重量、组成等物质属性，只从形状、位置、角度等方面认识物体，因此学生在认识图形过程中，教师要帮助他们完成以下抽象过程。

1.从实际物体到立体图形的抽象。学生在现实生活中，首先接触到的是立体的东西，如：房子、柜子、铅笔盒、球等，然后才会注意到立体图形的某个表面。因此学生的数学学习自然也会遵循这种认知规律。认识立体图形时，课前让学生收集一些包装盒子，并搭建自己喜欢的造型，说说自己用到了哪些形状的盒子。接着让学生将特点相同的盒子放到一起，即分一分，并起一个名字，然后从大量的统一形状的实际物体中抽象出长方体、正方体、圆柱、球等立体图形。

在教学中要利用多媒体帮助学生实现由实物到符号的抽象过程。例如：学生指出日常生活中见到过的物体的形状以后，课件演示将高楼、盒子的背景隐去，只留下形，从而抽象出立体图形。

2.从立体图形到平面图形的抽象。对于平面图形的抽象过程，可以从两个维度入手。一是从生活中实际物体面的形状的抽象，二是描述抽象完毕的立体图形的某个面。经历了这样的抽象过程，使数学生活化，帮助学生更好理解图形的来源和研究图形的背景，进而理解数学这门学科所研究的问题具有的抽象性。比如在一年级认识平面图形时，可以采取下面的方式：

（1）创设情境，激发想象。教学中教师首先创设一个形象的问题情境“立体图形的脚印”：大森林里下雪了，立体图形邀请一些小动物一起到雪地上玩。提问：想一想，这些立体图形会在草地上留下什么样的脚印呢？这实际上是激发学生根据立体图形的某个面想象平面图形。

（2）动手操作，拓印图形。教师提问：怎样能得到这些立体图形的脚印呢？学生想了很多办法，描一描，用印泥印一印等等。无论运用何种办法，在做的过程中，学生都会体会到平面图形是从立体图形上得到的。

（3）关注特征，分类命名。剪平面图形，并分类。把画好的脚印剪下来，贴到相应的位置。一边贴，一边想，得到的小脚印和谁是好朋友就把它贴在谁的下面。这实际上是一个简单的分类过程。观察平面图形，初步感知。

观察到的小脚印，你能发现什么？这实际上是依次观察每一类平面图形，感知每一类平面图形的特点。求同，并命名。

这些小脚印有什么共同的地方？你是怎么看的？这实际上是让学生说理的一个过程，也就是一个求同的过程，得出每一类图形的相同点，并给每一类图形命名。

这些图形和刚才的立体图形有什么关系？有什么不同的地方？这实际上是进一步体会“面”来自于“体”，沟通立体图形和平面图形的关系。

通过前面几个环节的活动，学生很好地完成了从立体图形到平面图形的抽象。可见，学生对图形的抽象是需要经历一个漫长感知过程的，不是一次就能够完成的。因此在教学中，教师要注重引导学生通过反复的观察、操作、想象来增强学生的体验。

二、经历图形分类与辨析的过程，感悟数学思想方法

分类是一种重要的数学思想。图形分类可以帮助学生对图形进行比较、概括，从而深入体会图形的特征。我们以“四边形的分类”为例，探讨分类的过程。

教师给学生提供若干个大小、形状不同的四边形，引导学生对其进行分类。具体如下：

深入推进流域水资源保护与水生态修复。加快流域水资源保护规划和水土保持规划编制。加大饮用水水源地、地下水保护力度，协调推动潘大水库周边综合整治工程实施、网箱养鱼清理和水生态补偿机制建设。以平原区风沙治理为重点大力推进流域水土保持生态修复。

1.观察比较，明确视角。仔细观察，这些图形都是四边形，但是它们有什么不一样的地方呢？（有的对边平行，有的对边相等，有的对边相等且平行，有的对角相等，有的对角不相等。教师可以根据学生的回答，简单板书。）

2.比较辨析，确定标准。同学们发现了这么多不同的地方，主要集中在哪些方面呢？（对边平行，对角相等，对边相等，四条边相等，四个角相等）找到研究问题的视角：从边和角入手。

3.根据标准，进行分类。填表格，并根据表格，填集合圈。

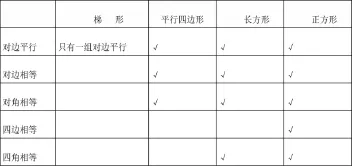
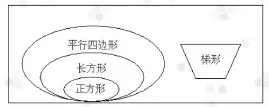
在这节课中，分类的标准是学生自己发现的。首先，观察比较。教师引导学生在观察的基础上发表自己的想法，发散学生的思维，把不同的地方尽可能地表达出来。其次，汇报聚焦。结合学生的汇报，将不同的地方集中在边和角上。再次，确定标准。根据边和角不同确定分类标准：对边是否平行、对角是否相等、四角是否相等、四边是否相等。最后，完成分类。借助于分类学生很自然地厘清了不同四边形之间的关系。

在这个过程中，分类标准是学生自己在观察比较中发现的，在比较辨析中确定的。不是教师告诉的。通过这节课的学习，学生掌握的不仅仅是四边形的分类，更习得了确定分类标准的方法以及研究图形特征的方法。

三、经历探索与发现的过程，累积数学活动经验

小学生获得第的对图形的表象是建立在视觉、触觉、听觉等大量感官活动的基础上的。因此，在教学这部分内容时，教师要尽可能地组织多样的学习活动，引导学生在活动中建立表象，积累数学活动经验。具体如下：

1.观察。观察是学生获取图形特征的最直接的方法。学生对很多图形特征的发现、猜想的提出等都是始于观察的。因此，教师要善于组织多种多样的观察活动，通过观察初步发展学生的空间观念。一方面，可以让学生观察静态的图形，初步感知图形的特征；另一方面，可引导学生观察动态的计算机演示，借以验证图形的特征，加深印象。观察前，教师要结合教学实际适时提出问题，引导学生借助于观察比较得出初步的结论、确定思考的维度、得出自己的认识。

2.操作。学生在观察的基础上会直观获得很多关于图形的经验，那么，这些发现是否可靠呢？就需要进一步的操作如撕、折、剪、拼、画等活动来验证。通过这些简单的操作活动能够进一步验证学生观察的结果，同时也能够发现一些通过观察所不能得到的图形的隐性特征。

4.猜想。学生的很多发现都始于猜想。因此在教学过程中，教师要善于引导学生敢于猜想。如：在学习三角形三条边的关系之前，教师就可以组织学生展开猜想，是不是只要给出三条线段，就一定能围成三角形呢？从而引发学生探究的热情。

5.推理。推理是人们生活与学习经常使用的思维方式，也是数学的基本思维方式。教师要善于引导学生通过合情推理进行验证。如：学生在验证正方形的四条边是否都相等这一特征时，先把正方形左右两条边对折，发现对边相等，然后再斜向对折，发现邻边相等。由此就能推理得出正方形四条边的长度都相等。

6.反思。学生探讨完图形的特征以后，教师还要适时的组织学生进行反思，从而引导学生有意识地反思回顾探索图形特征的方法、过程。荷兰著名数学家、数学教育家弗赖登塔尔早就有过精辟的论述：“儿童用逻辑方法组织活动的能力有着一个持续但并不连续的发展过程。在最初阶段，他们通过手、眼以及各种感觉器官进行思维，经过一段时间的亲身体验，通过主动的反思，就会客观地描述这些低层次的活动，从而进入一个较高的层次，帮助学生有效地积累数学活动经验。”

当然，在实际活动过程中，每个活动都不是单独展开的，很多时候是将几个活动相继或同时展开的。在活动中逐步积累直观经验和活动经验，发展学生有条理的思考和解决问题的能力。

下面以“三角形两边之和大于第三边”为例剖析学生积累活动经验的过程。

（1）直观观察，初步感知

提问：观察东东家和学校的示意图。

思考：东东每天从家去学校，怎样走最近？

课件演示：连接家、公园和学校，围成一个三角形。三角形里有很多问题值得研究，给你任意长的三根小棒，是不是都能围成三角形呢？

（2）操作探究

①教师给学生提供5根长度不同的小棒，供学生实验操作。分别是：9厘米、3厘米、6厘米、7厘米和5厘米。要求：任意选择3根，看一看能否围成一个首尾连接的三角形，并填写表格。

②观察课件演示，对于不能围成三角形的情况，思考：怎样才能围成三角形呢？

在观察中，学生发现，只有延长另外两根小棒的长度才能围成三角形。

③研究能够围成三角形的三根小棒，它们之间有什么关系？

该节课中，教师先后引导学生经历了两个层次的探究活动。一是否所有的三根小棒都能围成三角形？二是围成三角形的三根小棒具备什么特点？在这两个层次的探究活动中，教师先后多次引导学生进行了观察、操作和比较活动。在观察中初步发现规律，在比较中抽象出规律，明确问题。在这个过程中，学生积累了足够的活动经验，不仅有动手操作即实践经验，也有抽象思考即思维的经验，有效地发展了学生的空间思维，提升了学生的数学素养。

四、经历图形的转化过程，发展学生空间观念

“图形与几何”内容重要的目标之一是培养几何直观，发展空间观念。所谓空间观念是对空间中物体的位置、位置之间关系的感性认识，在数学课程标准中关于空间观念是这样叙述的：“主要是指能根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体；想象出物体的方位和相互之间的位置关系；描述图形的运动和变化；依据语言的描述画出图形。”

从上面的论述可以看到，建立空间观念的本质是为了提高学生的空间想象力。这个想象力既包括从现实物体到平面图形的抽象，也包括从平面图形到现实物体的想象。所以在图形的认识教学中，要结合内容，让学生经历图形之间的转化过程，帮助学生在头脑中建立起图形的直观表象，为学生提供想象的机会，以“展开与折叠”为例，教师引导学生经历了两个重要的转化过程。

1.正方体到平面展开图的转化。（1）想象：把正方体剪开，剪开的展开图会是什么样的？（2）操作：剪出尽可能与其他同学不同的展开图。（3）求同：转一转，看一看，哪些展开图实际上是相同的？（4）分类：根据展开图的特点进行分类。

2.平面展开图到正方体的转化。（1）动手折：用展开图直接折成正方体。（2）想象折：不动手，动脑想象怎样把展开图折成正方体。（3）验证想象：先利用展开图，想象着标出各面，然后动手折，验证想象是否正确。

纵观教学过程，既有动手的过程，也有思考、想象的过程，教师指导学生经历了两个重要的图形转化过程，沟通了两个重要的对应关系，即：立体图形和平面展开图之间的双向转化，想象和实物操作的双向转化；沟通立体图形和平面展开图之间的对应关系，沟通头脑想象和实物操作之间的对应关系，从而有效发展了学生的空间观念。

［1］姚莉华.“空间与图形”有效教学策略研究［J］.基础教育论坛，2011（11）.

［2］高俊生.小学数学教师“图形与几何”领域疑难问题分析［D］.长春：东北师范大学，2012.

［3］李光树.小学数学教学论［M］.人民教育出版社，2011.

［4］杨庆余.小学数学课程与教学［M］.北京：高等教育出版社，2004.

［5］蓝志辉.在操作体验中发展小学生的空间观念［J］.江西教育，2005（9）.

［6］周佩青.小学生空间观念的培养［J］.教学月刊（小学版），2005（10）.

（责任编辑：陈志华）