流域面源污染负荷差异性及不确定性的尺度特性分析

王 康，冉 宁，张仁铎，林忠兵

（1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072； 2. 中山大学环境科学与工程学院，广州 510275）

流域面源污染负荷差异性及不确定性的尺度特性分析

王 康1，冉 宁1，张仁铎2，林忠兵1

（1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072； 2. 中山大学环境科学与工程学院，广州 510275）

针对流域面源污染负荷差异性及其不确定性的尺度特性问题，于2013－2015年在釜溪河流域测定了不同尺度汇流区的面源污染负荷和污染物转化动力学参数。分别采用动态时间弯曲距离DTW（dynamic time warping distance）和信息测度度量了不同尺度汇流区面源污染的负荷差异性和不确定性。结果表明：不同的汇流区尺度上，降雨量小于临界值（40 mm）的情况下，氨氮（NH3）、总氮（TN）、总磷（TP），和高锰酸盐指数（IMn）负荷均随降雨量的增加而非线性增大，降雨量超过临界值后，流域面源污染出现最大负荷。降雨量超过临界值后，由于尺度增加后下垫面对径流过程调蓄能力的增大，相比子流域尺度，流域尺度上NH3、TN、TP和IMn负荷的变异系数分别增加了69.1%、47.0%、14.2%和85.8%。枯水期和汛期面源污染负荷主要受到污染源流域分布特性和下垫面径流条件的影响，不同尺度汇流区的NH3、TN、TP和IMn负荷在枯水期的差异性均显著小于汛期的差异性，子流域之间、以及子流域与流域之间4种污染负荷的差异性平均增大了3.18倍和2.44倍。相比子流域尺度，在流域尺度上单位面积流量、TN、TP和IMn负荷基质熵分别减小了4.8%、9.3%、31.9%和10.7%，而NH3增加了15.3%；有效测定复杂度分别增加了4.6%、15.4%、17.4%、49.5%和19.8%。不同尺度汇流区的面源污染负荷过程与流量过程不具有完全同步性。随着汇流区尺度的增大，面源污染负荷不确定性减小；有效测量复杂度随尺度增大表明在更大的尺度上对于面源污染负荷有效预测的参数数量显著增加；涨落复杂度和平均信息增量关系表明随着尺度的增加，面源污染负荷对降雨量的敏感性降低，而对下垫面条件的敏感性增加。不同尺度条件下，面源污染对降雨和下垫面的敏感性变化规律、以及面源污染负荷变异性机理等方面的研究将有助于提升分布式水文及面源污染模型理论。

污染；N；P；农业面源污染；流域尺度；动态时间弯曲距离；不确定性

0 引 言

来源于农田、农村生活和畜禽养殖、以及水土流失的农业面源污染的排放源强、径流过程、以及入河过程具有高度的时间和空间变异性[1-2]。分布式水文和面源污染迁移转化模型根据下垫面的差异，将流域划分为一系列相对独立的汇流区，在各汇流区内对水文和污染物迁移转化过程进行物理概化[3]，并通过设定不同的参数描述下垫面差异对水文和污染物迁移过程的影响[4-5]。由于不同下垫面对降雨-径流过程响应的敏感性不同[6-7]，不同径流条件下污染物迁移、转化能力及过程的差异[8-9]、以及汇流区初始条件和边界条件的差异，导致了面源污染负荷存在着显著的不确定性。污染物迁移转化过程的物理概化的关键在于确立汇流区主控驱动（如水文、生物、地球化学）过程与面源污染负荷之间的响应关系[10]，然而由于面源污染负荷的不确定性，即使在相同的驱动过程下，面源污染负荷亦表现出显著的波动[11]，掌握面源污染在不同的驱动条件（如降雨）下的波动范围、以及驱动-污染负荷响应关系发生趋势性变化的临界值将能够提升分布式模型的可靠性和精度。此外，分布式模型通常将下垫面的宏观特征参数作为模型的输入信息，然而下垫面不同土地利用类型形状、位置、相互关系等详细信息对于面源污染过程的影响及其尺度特性，则在一定程度上被忽略了[12]。更为重要的是，下垫面对径流过程的调节能力[13]以及污染源和下垫面信息量[14-15]都在很大程度上受到流域尺度的影响，然而现有研究尚不清楚在不同的流域尺度下的面源污染负荷变化规律及其不确定性。开展相关研究对于掌握流域污染物迁移转化规律、构建分布式水文及面源污染模型具有重要的意义。

本文在釜溪河流域，开展了3 a现场试验和监测，测定了不同汇流区尺度的面源污染负荷（单位面积的污染通量）以及动力学参数，基于动态时间弯曲距离DTW（dynamic time warping distance）研究了不同尺度面源污染负荷的差异性及其影响因素，基于信息测度分析了不同尺度的面源污染负荷变化及其不确定性。

1 试验与监测

1.1 流域基本情况与水质监测

釜溪河为沱江一级支流，流域基本情况如图1a所示，流域（29°60′-29°45′N, 104°18′-105°01′E）面积2 983 km2，地面高程262～959 m。旭水河和威远河是釜溪河的一级支流，旭水河流域面积967 km2，威远河流域面积1 036 km2。

流域内设有自贡、荣县、威远和富顺4个气象站（图1a）。配对t检验表明，流域内4个气象站监测年降雨过程并无显著性的差异。流域多年（1961－2015年）平均气温为17.9 ℃，多年平均、最大、最小降雨量分别为1 045、1 543和668 mm。汛期（5－10月）降雨量占年降雨量的76.2%。

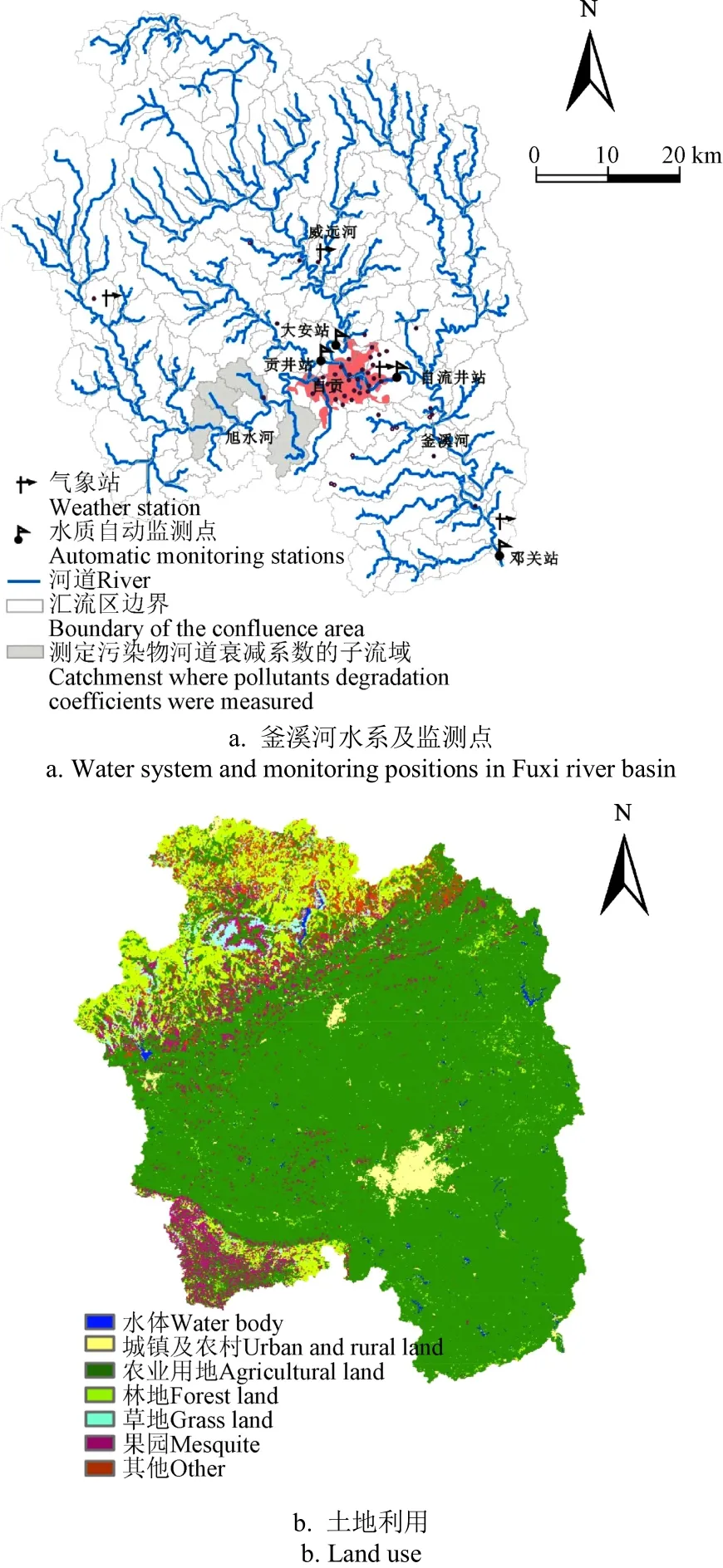
图1 釜溪河流域信息及污染监测点分布Fig.1 Basic information and monitoring position distribution in Fuxi river basin

流域土地利用类型如图1b所示，土地利用主要包括林地、农业用地、城镇及农村用地、果园、草地和水体等7种类型。旭水河子流域、威远河子流域以及釜溪河流域下垫面基本信息、面源污染源强以及径流条件的比较如表1所示。

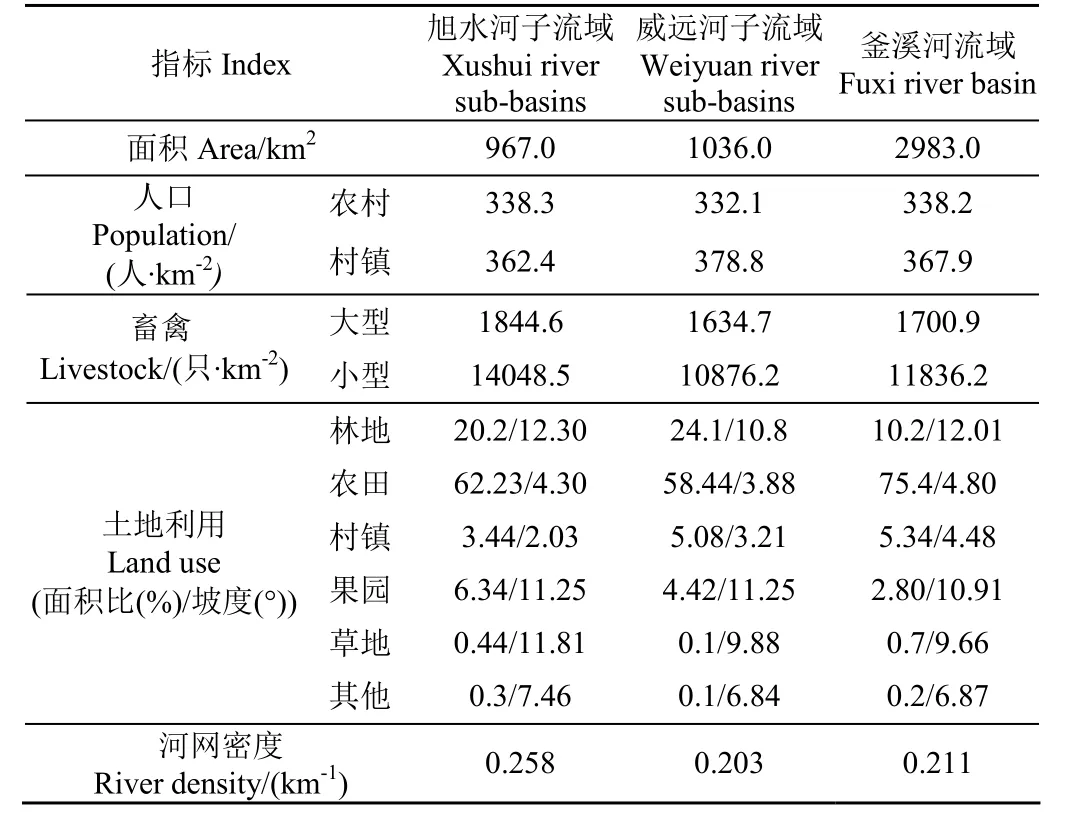
表1 研究区基本情况Table 1 Basic information of studied region

选择作为河道水质评价指标，且来源和径流过程显著不同的氨氮（NH3）、总氮（TN）、总磷（TP）和高锰酸盐指数（IMn）等4种污染物作为研究对象。在旭水河出口（贡井站），威远河出口（大安站），釜溪河自贡市城区下游（自流井站）和釜溪河出口（邓关站）位置，设置了水质自动监测站（图1a），2013年2月开始对干支流河道流量以及NH3、TN、TP和IMn质量浓度进行逐日监测。

由于河道自动监测站的水质监测结果包括了点源和面源的贡献，面源污染通量需要扣除点源污染的贡献。釜溪河流域76%的工业点源排放以及城市生活污水排放集中在自贡市城区（图1a），因此将自贡市城区作为集中点源，根据釜溪河自贡市城区出口断面（自流井站）以及城区入口断面（贡井站和大安站）监测的污染物通量，采用质量均衡法确定城区入河源强。其他主要点源入河量根据点源污水排放量及污染物质量浓度监测结果确定。

1.2 河道污染物衰减动力学系数测定

2014年和2015年在汛期和枯水期分别测定了河道中的污染物衰减动力学系数。选择14个汇流区内没有点源、且下垫面条件相似的封闭子流域（图1b），在子流域河道出口位置设置监测断面，汛期选择降雨开始~降雨结束后1 d，枯水期选择无降雨条件下连续3 d对子流域河道流量和污染物质量浓度进行监测，降雨时根据流量变化，每日进行8~10次监测，枯水期每日进行3次测定。污染物质量浓度由四川省环境监测总站测定，流量采用多普勒流速仪测定，汛期和枯水期分别进行了6次和4次测定。

河道污染物衰减动力学系数根据质量均衡法确定，第i个子流域出口断面通量表示为[16]：

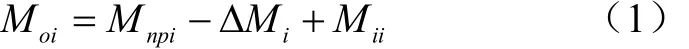
式中Mii和Mnpi分别为上游进入的污染物通量和子流域面源污染入河通量，g/d；ΔMi为污染物在子流域河道中的动力学衰减量，g/d。河道中的污染物衰减满足一阶动力学过程，衰减量ΔMi为[16]

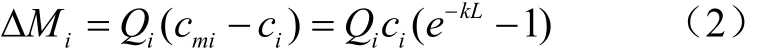
式中ci为子流域污染物出口质量浓度，mg/L；cmi为子流域入河污染物与上游污染物掺混后的质量浓度，mg/L；k为河道中污染物衰减动力学系数，km-1；L为子流域河道长度，km。子流域内面源污染物入河量为子流域面积与单位面积的污染入河量的乘积，子流域出口质量浓度可表示为[16]

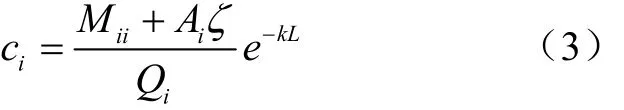
式中Ai为第i个子流域的面积，km2；ζ为单位面积的污染入河量，g/km2；Qi为子流域出口流量，m3/s。根据14个子流域的流量以及污染物质量浓度监测结果，基于式（3）分别对汛期和枯水期单位面积的面源污染入河量以及河道中污染物衰减动力学系数进行拟合。面源污染通量为控制断面监测通量与发生衰减后的点源通量之差。

1.3 下垫面及面源污染负荷差异性评价指标

下垫面的差异性评价指标参数包括：单位面积农村和城镇人口、大型和小型畜禽养殖数量等4个反映污染源强特性的指标参数；林地、农田、村镇、果园、草地和其他6种土地利用类型的面积比例等6个反映土地利用情况的指标参数；以及6种土地利用类型的坡度和河网密度等7个反映径流条件的指标参数（表1）。采用du描述不同尺度流域下垫面的差异

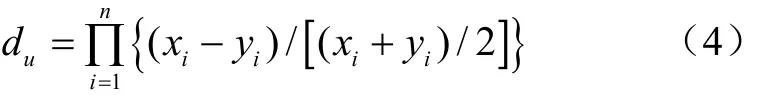
式中下标i为下垫面指标参数，n为子流域之间或子流域和流域之间进行比较的指标参数数量，x和y分别表示进行比较的流域或子流域。

考虑到流域尺度对产汇流过程的影响，为了使不同尺度流域之间的面源污染负荷具有可比性，采用动态时间弯曲距离（DTW）对面源污染负荷时间序列的差异进行比较。长度为m的2个时间序列X = {x1, x2, …xi, …, xm}和Y = {y1, y2, …, yj…, ym}形成m×m矩阵，矩阵中（i, j）位置的值为2个进行比较的时间序列在时刻i和j之间的欧氏距离。2个时间序列的DTW距离为[17]

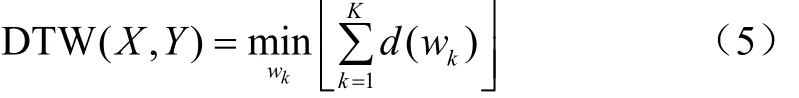
式中d为欧式距离，wk=(xi, yj)为矩阵中xi和yj之间的最短距离，K为总路径，污染负荷时间序列在子流域之间或子流域与流域之间的DTW距离越短，则污染负荷在对比尺度上的差异性越小。

1.4 面源污染负荷不确定性度量

将时间序列小于均值的负荷值设定为0，大于和等于均值的负荷值设定为1，将时间序转换为二值序列，如图2所示。以污染负荷的连续3日二值序列[21]为指标进行考察，则污染负荷时间序列包括了000，010，001，100，101，110，011和111等8种状态，分别采用基质熵E、平均信息增量T对面源污染不确定性进行度量，采用涨落复杂度σ2和有效测量复杂度CEM对时间序列的复杂性进行度量。

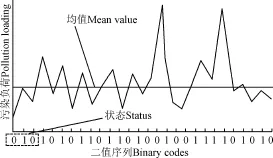
图2 污染负荷时间序列二值化示意图Fig.2 Illustration of binary encoding of time series for pollution loading

信息熵定义为[18]

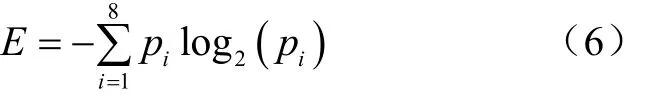
基质熵为标准化后的信息熵（信息熵/最大值），熵值越大，系统越紊乱，其不确定性也越显著。

平均信息增量定义为[19]：

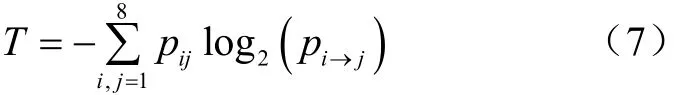
式中ip为第i种状态的概率，ijp为状态i和状态j先后发生的概率，ijp®为第i种状态向第j种状态变化的概率。

涨落复杂度定义为[20]

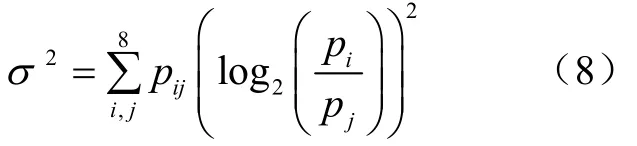
涨落复杂度用于度量面源污染负荷对降雨以及下垫面条件的敏感性。

有效测量复杂度定义为[21]

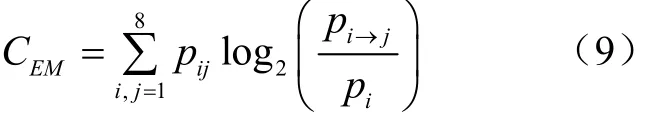
有效测量复杂度越大，需要更多的参数才能够实现污染负荷的有效预测。

2 面源污染负荷差异性分析

2.1 单次降雨面源污染负荷差异性分析

2013－2015年共发生了124次降雨，图3a～3d为2013－2015年流域（釜溪河流域）和子流域（旭水河子流域和威远河子流域）2个尺度下，单次降雨NH3、TN、TP和IMn负荷与降雨量的比较。基于Mann-Kendall检验[22]可知，在95%显著水平下，降雨量小于40 mm（临界值）的情况下，2个尺度4种面源污染物负荷随降雨量的增大而非线性增大，降雨量超过临界值后，2个尺度4种面源污染的负荷均保持稳定，不再增大，表明不同尺度的流域面源污染均出现最大负荷。其中原因在于：在降雨量较小的情况下，由于入渗和填洼，以及泥沙的起动能力的不足，面源污染物主要在临近河道、坡度较大、以及土壤入渗率低等污染物易于入河的区域进入河道，随着降雨的增加，在更大的区域内形成径流入河条件以及泥沙的起动入河，面源污染负荷随着汇流入河区域的增大而增加，当降雨超过临界值时，整个汇流区内形成入河径流条件，由于汇流区域面积不在增加，以及下垫面对径流的调节能力达到饱和，面源污染负荷不再增大。4种迁移特性显著不同的面源污染负荷均不再发生显著变化，亦表明了最大负荷主要受汇流区域面积的影响。

表2为降雨量小于和超过临界值后4种污染物污染负荷变异系数（标准差/均值）的比较。降雨量小于临界值的情况下，流域和子流域2个尺度的变异系数没有显著的差异，而降雨量超过临界值后，流域尺度的变异系数增大。相比子流域尺度，在流域尺度上NH3、TN、TP和IMn负荷的变异系数分别增加了69.1%、47.0%、14.2%和85.8%。这一结果表明，不同降雨量条件下，影响面源污染负荷的因素发生了显著的变化：降雨小于临界值的条件下，面源污染负荷主要受到下垫面初始状态、降雨强度及过程[23-24]、不同面源污染物的来源以及迁移过程的影响，而降雨量超临界值后，面源污染物主要通过地表径流的形式入河，尺度增加后由于下垫面对径流调节能力的增加，导致了污染负荷变异性发生趋势性的变化。

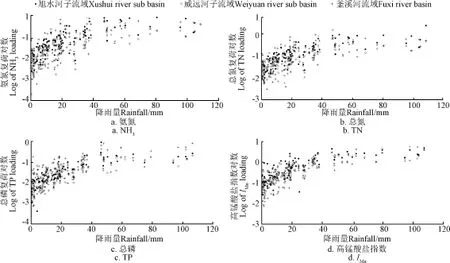
图3 旭水河、威远河子流域和釜溪河流域NH3、TN、TP和IMn负荷随降雨量的变化Fig.3 Non-point source pollution loading of NH3, TN, TP, and IMnvaried with rainfall values for Xushui and Weiyuan river sub-basins and Fuxi river basin

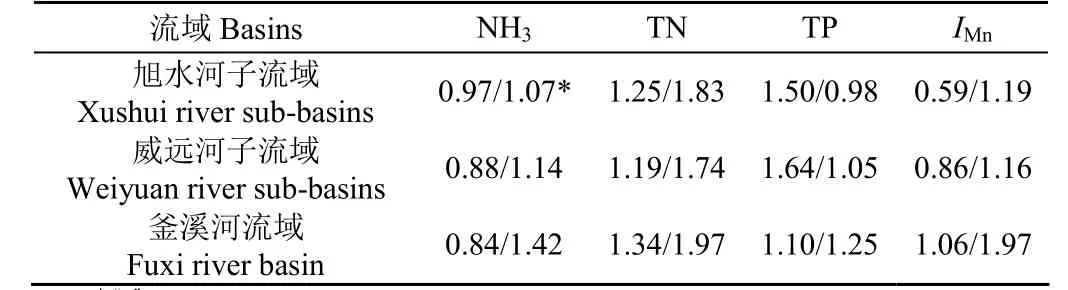
表2 临界降雨前后NH3、TN、TP、IMn负荷变异系数的比较Table 2 Coefficients of variation of loading of NH3, TN, TP andIMnfor different rainfall events

图4a～4d分别为单位降雨NH3、TN、TP和IMn负荷的概率密度分布，与流域尺度相比，单位降雨污染负荷的概率分布在子流域尺度中更为集中：NH3、TN、TP和IMn的单位降雨量负荷在均值±标准差区间内的累积概率分别为0.676、0.667、0.722和0.686。而在流域尺度，累积概率则分别为0.564、0.625、0.476和0.557，相比子流域尺度，在均值±标准差区间，4种污染物在流域尺度的累积概率减小了7.3%～36.2%，概率峰值下降了12.4%～27.2%。相比其他污染物，主要来源于农村生活和畜禽养殖的IMn，其密度函数在2个尺度中均表现出多个峰值，这主要是由农村生活和畜禽养殖分散源强特性决定的，而对于主要来源于土壤、且受到连续径流过程影响的NH3、TN和TP，则质量浓度峰值主要是由于污染物随着降雨量增加而表现出非线性增长所造成的。

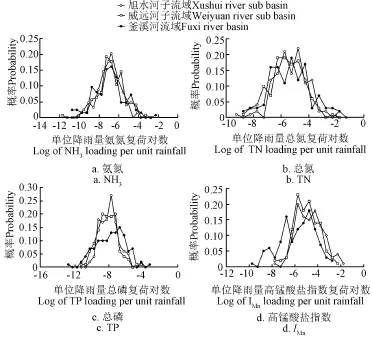
图4 旭水河、威远河子流域和釜溪河流域NH3,TN，TP和IMn的单位降雨负荷概率分布Fig.4 Probability density distributions of NH3, TN, TP and IMnloads per unit rainfall for Xushui and Weiyuan river sub-basins and the Fuxi river basin

2.2 不同水文期面源负荷差异性分析

图5为旭水河子流域、威远河子流域和釜溪河流域2013－2015年NH3、TN、TP和IMn负荷时间序列比较。汛期和枯水期，单位面积流量和4种污染负荷在流域和子流域之间以及子流域之间的DTW距离如表3所示。表3亦同时对标准化后（监测值-均值）的单位面积流量和污染负荷在流域和子流域之间以及子流域之间的DTW距离进行了比较。汛期NH3、TN、TP和IMn在河道中的衰减动力学系数分别为0.104、0.047、0.042和0.112 km-1，枯水期4种污染物在河道中的衰减动力学系数分别为：0.07、0.029、0.022和0.08 km-1，尽管不同水文期以及不同污染物的河道衰减动力学系数存在较大差异，然而由表3可知，枯水期和汛期，标准化后的单位面积流量和4种污染负荷时间序列的DWT距离与实测时间序列的DWT距离偏差均小于5%，表明河道水文过程中污染物的衰减动力学过程并不显著影响面源污染负荷的尺度差异性，不同尺度的面源污染负荷差异性主要受到陆面水文过程的影响。

相比枯水期（10－4月），汛期（5－9月）子流域之间、以及子流域和流域之间4种污染负荷的DWT距离均显著增加（表3）。在汛期和枯水期，子流域之间IMn负荷的DWT距离均大于子流域与流域之间的DWT距离，其主要原因在于：IMn负荷主要来源于分散于流域的农村生活和畜禽养殖，不同水文期降雨径流过程对其影响较小。下垫面影响IMn负荷的指标参数包括单位面积农村人口、单位面积大型和小型畜禽养殖数量、以及河网密度（表1），基于这些指标参数（n=4），采用式（4）计算反映不同尺度流域下垫面差异的du值分别为0.286（旭水河子流域vs.威远河子流域），0.189（旭水河子流域vs.釜溪河流域）和1.948（威远河子流域vs.釜溪河流域），与不同尺度流域之间的IMn负荷的差异性一致。枯水期NH3、TN和TP负荷主要受农村和城镇生活，以及畜禽养殖等污染源分布的影响，而在汛期，则污染源分布、土地利用和径流条件均对NH3，TN和TP负荷产生影响，基于表1中全部指标参数（n=17）计算得du值分别为0.813（旭水河流域vs.威远河流域），1.513（旭水河子流域vs.釜溪河流域），1.948（威远河子流域vs.釜溪河流域）。可以看出，考虑全部指标参数的情况下，子流域和流域之间下垫面的差异要显著大于子流域之间的差异，是子流域之间的NH3、TN和TP负荷的差异性小于子流域与流域之间的负荷差异性的主要原因。

图5 2013－2015年旭水河、威远河和釜溪河流域NH3，TN，TP和IMn负荷的比较Fig.5 Comparison of daily non-point source pollution loading of NH3, TN, TP, and IMnfor the Xushui and Weiyuan river sub-basins and Fuxi river basin from 2013 to 2015

表3 单位面积流量及污染负荷在流域和子流域之间以及子流域之间的DTW距离比较Table 3 Comparison of dynamic time warping distances of water flow rates and loading of NH3, TN, TP, and IMnbetween basin and sub-basin and between sub-basins

土壤和农田中的NH3和TP主要通过地表径流以溶解质和悬移质携带的形式入河，而TN则通过多种径流途径（地表径流、土壤渗流以及地下水）进入河道[25-26]，因而造成了不同尺度流域之间TN负荷的差异性显著的超过NH3和TP负荷的差异性（表3）。

3 面源污染负荷不确定性分析

表4为不同尺度流域2013－2015年单位面积流量和面源污染负荷时间序列基质熵、平均信息增量、有效测量复杂度和涨落复杂度的比较。相比水文流量的基质熵，污染负荷的基质熵更接近于1。旭水河和威远河子流域尺度上，污染负荷的基质熵相比流量分别增加了17.4%（NH3）、28.5%（TN），35.4%（TP）和21.4%（IMn），而在流域尺度上，污染负荷的基质熵相比流量分别增加了45.3%、23.2%、7.6%和15.0%。在不同尺度上，污染物的基质熵增加幅度并没有显著的差异。然而，子流域尺度上4种污染负荷的有效测量复杂度相比流量分别减小了31.9%、30.5%、34.4%和23.1%，而在流域尺度上，则分别减小了24.6%、22.1%、6.6%和11.9%，流域尺度的4种污染物有效测量复杂度变幅明显小于子流域尺度的变幅，这一结果表明，不同的尺度下，流量过程和污染负荷过程不具有完全同步性。4种污染物中，不同尺度流域TP负荷的基质熵和有效测量复杂度的差异性最为显著，随着流域的增加，TP负荷的可预测性发生显著的变化，相比NH3和TN负荷，尺度增大后，TP负荷的不确定性更为明显[27-30]。IMn由于主要受到污染源分布的影响，受下垫面差异性的影响较小，因此4种污染负荷中，其在子流域和流域尺度的差异性最低。

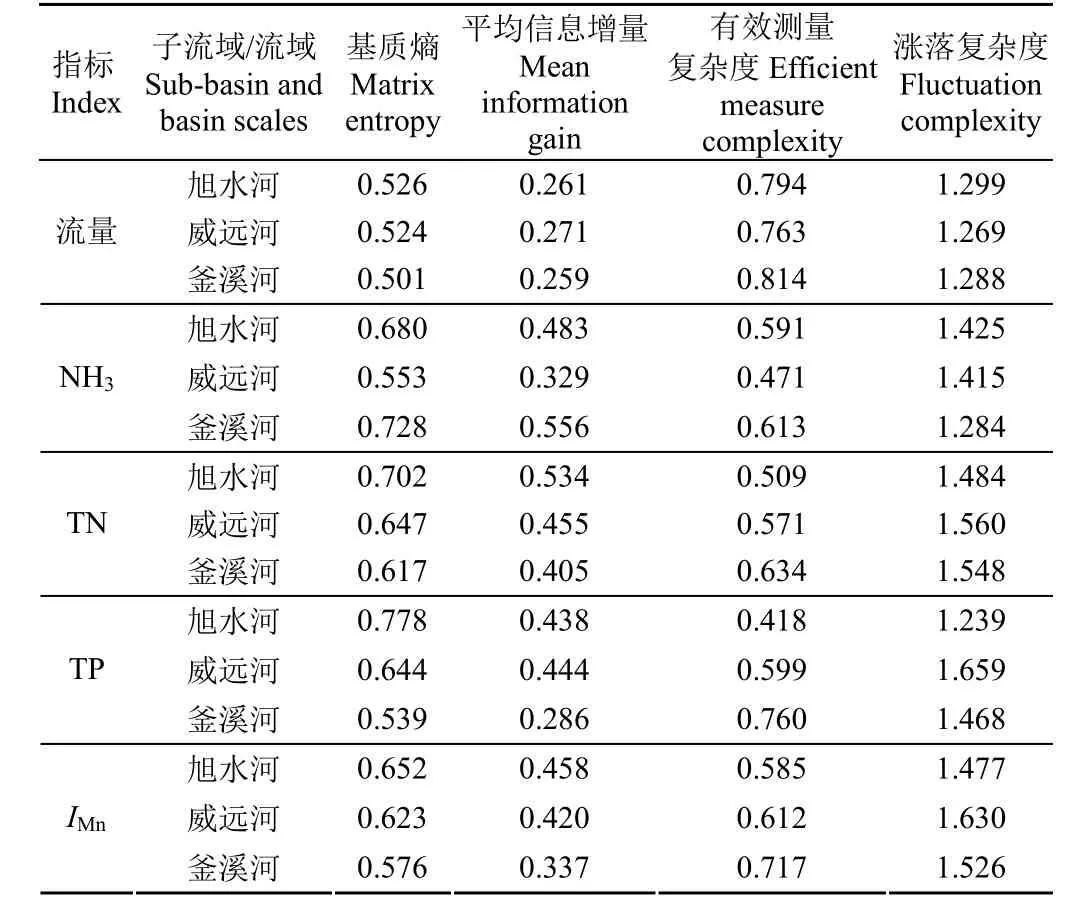
表4 不同尺度流域面源污染负荷信息和复杂性测度Table 4 Complexity and information measures for non-point pollution loading at sub-basin and basin scales

由表4可知，4种面源污染负荷的基质熵值均随着尺度的增加而减小，相比子流域尺度，除NH3（增加15.3%）外，在流域尺度上单位面积流量、TN、TP和IMn负荷的信息熵值分别减小了4.8%、9.3%、31.9%和10.7%，表明面源污染负荷的不确定性随着尺度的增大而减小；污染负荷的有效测量复杂度随着流域尺度的增加而增大，有效测定复杂度分别增加了4.56%、15.4%、17.4%、49.5%和19.8%，表明在更大的尺度上实现面源污染的有效预测，所需要基本信息量（参数）的数量将显著增加。旭水河、威远河子流域和釜溪河流域单位面积流量，NH3、TN、TP和IMn时间序列的涨落复杂度与平均信息增量关系如图6所示，可以看出水文流量所占的区域较为集中，而在流域尺度上，4种污染物所占的区域范围（图6中的深灰色区域）显著的超过子流域尺度中4种污染物所占的区域范围（图6中的浅灰色区域），表明随着流域尺度的增加，尽管面源污染负荷的不确定性减小，然而其复杂性显著增加，导致可预测性降低，也表明随着流域的增大，面源污染负荷对于降雨的敏感性下降，而对于下垫面的敏感性增大。

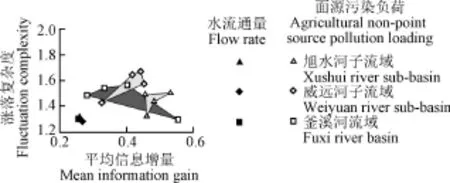
图6 不同尺度单位面积流量与面源污染负荷涨落复杂度与平均信息增量关系Fig.6 Fluctuation complexity vs. mean information gain of daily runoff and pollution loading for Xushui and Weiyuan river sub-basins and Fuxi river basin.

4 结 论

2013－2015年，在釜溪河流域，针对流域面源污染负荷及其不确定性的尺度特性问题，开展了系统的试验与监测。

农业面源污染负荷随降雨量增大而非线性增大。降雨量超过临界值（40 mm）后，流域面源污染出现最大负荷，降雨量在临界值前后，面源污染负荷与降雨量关系均表现出显著的变异性，降雨量小于临界值情况下，子流域和流域面源污染负荷并无显著差异，降雨量超过临界值后，由于尺度增加后下垫面对径流过程调蓄能力的增大，相比子流域尺度，流域尺度上NH3、总氮TN、总磷TP和高锰酸盐指数IMn负荷的变异系数分别增加了69.1%、47.0%、14.2%和85.8%。

基于动态时间弯曲距离（DTW）度量了不同尺度汇流区的污染负荷的差异性。结果表明：不同尺度的流域面源污染负荷的差异性主要受到陆面水文过程的影响。相比枯水期，汛期污染负荷的差异性显著增加，子流域之间、以及子流域与流域之间4种面源污染负荷的差异性平均增大了3.18倍和2.44倍。

面源污染负荷的不确定性随尺度的增加而降低，对面源进行预测的基础信息量则随着尺度的增加而显著增大；相比子流域尺度，除NH3（增加15.3%）外，在流域尺度上单位面积流量、TN、TP和IMn负荷的信息熵值分别减小了4.8%、9.3%、31.9%和10.7%，有效测定复杂度分别增加了4.6%、15.4%、17.4%、49.5%和19.8%。不同尺度流域的面源污染负荷过程与流量过程不具有完全同步性。随着流域尺度的增大，面源污染负荷对降雨的敏感性降低，对下垫面的敏感性增大。

需要指出，对不同尺度降雨和下垫面的敏感性变化机理、以及面源污染负荷尺度变异性的深入研究将有助于进一步提升分布式水文及面源污染模型理论。

[1] Andréassian V, Perrin C, Michel C, et al. Impact of imperfect rainfall knowledge on the efficiency and the parameters of watershed models[J]. Journal of Hydrology, 2001, 250(1/2/3/4): 206－223.

[2] Shen Z, Chen L, Liao Q, et al. Impact of spatial rainfall variability on hydrology and nonpoint source pollution modeling[J]. Journal of Hydrology, 2012, 472(24): 205－215.

[3] 李颖，王康，周祖昊. 基于SWAT模型的东北水稻灌区水文及面源污染过程模拟[J]. 农业工程学报，2014，30(7)：42－53. Li Ying, Wang Kang, Zhou Zuhao. Simulation of drainage and agricultural non-point source pollutions transport processes in the paddy irrigation district in North-East China using SWAT[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(7): 42－53. (in Chinese with English abstract)

[4] 张展羽，司涵，孔莉莉. 基于SWAT模型的小流域非点源氮磷迁移规律研究[J]. 农业工程学报，2013，29(2)：93－100. Zhang Zhanyu, Si Han, Kong Lili. Migration of non-point source nitrogen and phosphorus in small watershed based on SWAT model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(2): 93－100. (in Chinese with English abstract)

[5] 代俊峰，崔远来. 基于SWAT的灌区分布式水文模型－I.模型构建的原理与方法[J]. 水利学报，2009，40(2)：145－152. Dai Junfeng, Cui Yuanlai. Distributed hydrological model for irrigation area based on SWAT: I. Principle and method[J]. Journal of Hydraulic Engineering, 2009, 40(2): 145－152. (in Chinese with English abstract)

[6] Cherry K A, Shepherd M, Withers P J A, et al. Assessing the effectiveness of actions to mitigate nutrient loss from agriculture: A review of methods[J]. Science of the Total Environment, 2008, 406(1/2): 1－23.

[7] Ponader K C, Charles D F, Belton T J. Diatom-based TP and TN inference models and indices for monitoring nutrient enrichment of New Jersey streams[J]. Ecological Indicators, 2007, 7(1): 79－93.

[8] Shen Z, Hong Q, Yu H, et al. Parameter uncertainty analysis of the non-point source pollution in the Daning River Watershed of the Three Gorges Reservoir Region, China[J]. Science of the Total Environment, 2008, 405: 195－205.

[9] Liu R, Xu F, Zhang P, et al. Identifying non-point source critical source areas based on multi-factors at a basin scale with SWAT[J]. Journal of Hydrology, 2016, 533: 379－388. [10] Zahmatkesh Z, Karamouz M, Nazif S. Uncertainty based modeling of rainfall-runoff: Combined differential evolution adaptive Metropolis (DREAM) and K-means clustering[J]. Advances in Water Resources, 2015, 83: 405－420.

[11] Sun Y, Guo Q, Liu J, et al. Scale effects on spatially varying relationships between urban landscape patterns and water quality[J]. Environment Management, 2014, 54: 272－287.

[12] Ongley E D, Zhang X, Yu T. Current status of agricultural rural non-point source pollution assessment in China[J]. Environment Pollution, 2010, 158: 1159－1168.

[13] Zahmatkesh Z, Karamouz M, Nazif S. Uncertainty based modeling of rainfall-runoff: Combined differential evolution adaptive Metropolis (DREAM) and K-means clustering[J]. Advances in Water Resources, 2015, 83: 405－420.

[14] Zhang H, Huang G H. Assessment of non-point source pollution using a spatial multicriteria analysis approach[J]. Ecological Modelling, 2011, 222(2): 313－321.

[15] Mostofa Amina M G, Tamie L V, Amy S C. Simulating hydrological and nonpoint source pollution processes in a karst watershed: A variable source area hydrology model evaluation[J]. Agricultural Water Management, 2017, 180(31): 212－223

[16] Wang K, Lin Z, Zhang R. Impact of phosphate mining and separation of mined materials on the hydrology and water environment of the Huangbai River basin, China[J]. Science of the Total Environment, 2016, 543: 347－356.

[17] Giorgino T. Computing and visualizing dynamic time warping alignments in R: the package[J]. Journal of Statistical Software, 2009: 31: 1－24.

[18] Shannon C E. A mathematic theory of communication[J]. Bell System Technical Journal, 1948, 27: 379－423.

[19] Pachepsky Y, Guber A, Jacques D, et al. Information content and complexity of simulated soil water fluxes[J]. Geoderma, 2006, 134: 253－266.

[20] Grassberger P. Toward a quantitative theory of selfgenerated complexity[J]. International Journal of Theoretical Physics, 1986, 25: 907－938.

[21] Wang K, Zhang R, Yasuda H. Characterizing heterogeneous soil water flow and solute transport using information measures[J]. Journal of Hydrology, 2009, 370(1/2/3/4): 109－121.

[22] Ozgur K, Murat A. Comparison of Mann–Kendall and innovative trend method for water quality parameters of the Kizilirmak River, Turkey[J]. Journal of Hydrology, 513(26): 362－375.

[23] Fang N F, Shi Z H, Li L, et al. Rainfall, runoff, and suspended sediment delivery relationships in a small agricultural watershed of the Three Gorges area, China[J]. Geomorphology, 2011, 135(1): 158－166.

[24] Tuset J, Vericat D, Batalla R J. Rainfall, runoff and sediment transport in a Mediterranean mountainous catchment[J]. Science of the Total Environment, 2016, 546: 114－132.

[25] Bruun J, Pugliese L, Christian C, et al. Solute transport and nitrate removal in full-scale subsurface flow constructed wetlands of various designs treating agricultural drainage water[J]. Ecological Engineering, 2016, 97: 88－97.

[26] Thi N, Trang T, Shrestha S, et al. Evaluating the impacts ofclimate and land-use change on the hydrology and nutrient yield in a transboundary river basin: A case study in the 3S River Basin (Sekong, Sesan, and Srepok)[J]. Science of the Total Environment, 2017, 15: 586－598.

[27] Wade A J, Whitehead P G, Butterfield D. The Integrated Catchments model of Phosphorus dynamics (INCA-P), a new approach for multiple source assessment in heterogeneous river systems: model structure and equations[J]. Hydrology and Earth System Sciences, 2002, 6: 583－606.

[28] Jackson-Blake L A, Skeffington R A, Wade A J, et al. How well can we model stream phosphorus concentrations in agricultural catchments?[J]. Environmental Modelling & Software, 2014, 64(C): 31－46.

[29] Dupas R, Delmas M, Dorioz J M, et al. Assessing the impact of agricultural pressures on N and P loads and eutrophication risk[J]. Ecological Indicators, 2015, 48: 396－407.

[30] Dean S, Freer J, Beven K, et al. Uncertainty assessment of a process-based integrated catchment model of phosphorus (INCA-P)[J]. Stochastic Environmental Research & Risk Assessment, 2009, 23(7): 991－1010.

Analysis on characterization of heterogeneities and uncertainty for non-point source pollution loads at different basin scales

Wang Kang1, Ran Ning1, Zhang Renduo2, Lin Zhongbin1
(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China; 2. School of Environmental Science and Engineering, Sun Yat-sen University, Guangzhou 510275, China)

The objectives of this study were to characterize heterogeneities in agricultural non-point source (NPS) pollution loads, and to identify the uncertainty of time series of water flow and NPS pollution loadings at different scales. The Daily flow rates, concentrations of ammonium nitrogen (NH3), total nitrogen (TN), total phosphorus (TP), and the permanganate index (IMn) and the degradation coefficients of pollutants were measured in a river basin during the period from 2013 to 2015. The dynamic time warping distance (DTW) was used to characterize the differences of runoff flow rates and NPS pollution (i.e., NH3, TN, TP, and IMn) loadings under different underlying surfaces at the sub-basin and basin scales. Information entropy and complexity were used to measure the uncertainty and predictability of different variables at the 2 scales. At both sub-basin and basin scales, NPS pollution loadings increased nonlinearly with rainfall until the rainfall reached 40 mm, and then the NPS pollution loadings maintained stable. The coefficients of variation for NH3, TN, TP, and IMnat the basin scale were 69.1%, 47.0%, 14.2%, and 85.8% higher than those at the sub-basin scale, respectively, with the rainfall higher than the threshold amount. During the dry seasons, the differences in NPS pollution loads between the sub-basins were higher than those between the sub-basins and basin, which were mainly affected by the different pollution sources in the regions. The differences in NPS pollution loadings were significantly higher during the wet seasons than during the dry seasons at both the sub-basin and basin scales. Compared with the NPS pollution loads during the dry seasons, the differences in the NPS pollution loads between the 2 sub-basins and between the sub-basins and the basin increased by 3.18 times and 2.44 times, respectively, during the wet seasons. The differences in fluxes of NH3, TN, and TP between the sub-basins and between the sub-basins and basin were mainly attributed to the underlying surface conditions and the pollutions sources. Compared with the results at the sub-basin scale, the information entropy values for the time series of the water flux per unit area, TN, TP and IMnloads at the basin scale were decreased by 4.8%, 9.3%, 31.9% and 10.7%, respectively, but NH3were increased by 15.3%. The efficient measure complexity increased with the spatial scale. Compared with the sub-basin scale, the efficient measure complexity values at the basin scale for the water flux per unit area, NH3, TN, TP and IMnloads increased 4.6%, 15.4%, 17.4%, 49.5% and 19.8%, respectively. The result indicated that more parameters were required at the basin scale than at the sub-basin scale for the efficient prediction. The NPS pollutions load and flow processes were not synchronous at different spatial scales. For the flow rates and the NPS pollution loads, the information entropy decreased and effective measure complexity increased with the basin scales, indicating that the uncertainty decreased and the predictability decreased with the scales. The investigation on the sensitivity of NPS loadings to the rainfall and underlying surface at different scale, and physical basis of the NPS loadings at different scales will provide an insight into the theories of distributed hydrology and NPS simulation model.

pollution; nitrogen; phosphorus; agricultural non-point source pollution; basin scales; dynamic time warping distance; uncertainty

10.11975/j.issn.1002-6819.2017.11.027

X592

A

1002-6819(2017)-11-0211-08

王 康，冉 宁，张仁铎，林忠兵. 流域面源污染负荷差异性及不确定性的尺度特性分析[J]. 农业工程学报，2017，33(11)：211－218.

10.11975/j.issn.1002-6819.2017.11.027 http://www.tcsae.org

Wang Kang, Ran Ning, Zhang Renduo, Lin Zhongbin. Analysis on characterization of heterogeneities and uncertainty for non-point source pollution loads at different basin scales[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(11): 211－218. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.11.027 http://www.tcsae.org

2016-10-10

2017-05-12

国家自然科学基金（51379152，51679257）；国家重点研发计划（2016YFC0402405）

王 康，男，陕西安康人，教授，博士，主要从事农业面源污染方面的研究工作。武汉 武汉大学水资源与水电工程科学国家重点实验室，430072。Email：wwangkang@163.com