挖掘古代数学文化打赢2017高考攻坚战

东北育才双语学校 王海涛

将中国古代数学文化融入高考试题的意义毋庸置疑，在众多的文章中多有评述；将中国古代数学文化融入高考试题的途径想必同学们通过往届试题也心领神会.问题的关键不单是考过的那些试题，还在于我们应该了解更多的中国古代数学文化，去面对新的高考问题.为此，本文从高考可能涉及到的中国古代数学文化的相关内容、基本原理、可能结合的方法等，将问题分为代数部分、几何部分两方面进行阐述，有的配备了经典试题以助于理解，希望对同学们有所帮助.

一、与代数相关的古代数学文化内容

1.《周易》

《周易》是世界公认的第一本讨论排列的书，“易”就是变易的意思，书中使用一些特殊的符号，通过阴、阳、卦、爻来说明一些运动变化的道理，富有辩证思想.

《周易》与排列

每次取3个，共有8中不同的排列，叫做“八卦”：

八卦常用来代表不同的事物，如东、东南、南、西南、西、西北、北、东北八个方位，或天、地、风、雷、水、火、山、泽八种自然物等.八个方位和八卦对应起来，常画在罗盘的周围.同时与数学中的数轴（正、负两个方向），平面四个象限、空间八个卦限都是对应的.

《周易》与二进制

如将阳爻看作数字1，阴爻看作数字0，四象、八卦可以改写成为二进制数：

我们可以命制这样的试题：

例1受到中国“伏羲八卦图”的启发，德国数学家莱布尼茨发现了二进制.下表是其局部，依据表中规律，表中A、B应依次填入____.

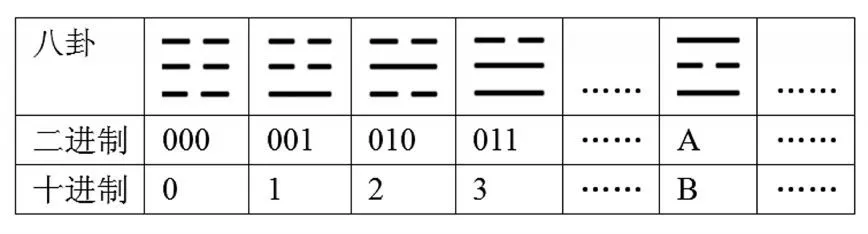
【答案】101，5

2.算筹

“运筹帷幄之中，决胜千里之外”这句话我们耳熟能详，什么是“筹”？就是算筹.在14世纪以前，我国的计算工具一直是一种细长的小棍棒，通常是用竹子、木头或骨头制成，这就是算筹.

用算筹表示数目，有纵横两种方式：

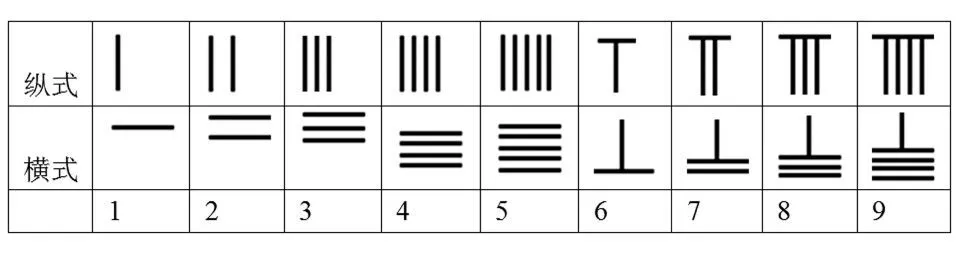
记数时，个位常用纵式，其余横纵相间.例如1949表示为

算筹可以进行加、减、乘、除、乘方、开方等运算.在《九章算术》中用算筹把线性方程组示成矩形的方阵：

3.位值制

位值制的特点是同一个数字由于它所在的位置不同而表示不同的值.例如1949，左边的数字“9”表示九百，右边的数字“9”表示九个.

我国是世界上最早采用进位制而又是十进位计数法的国家，特别是以个、十、百、千、万等专有名词表示每位数的地位，更比其他国家早.而“半斤八两”是因为我国过去曾经使用过16进位制的度量衡工具——秤，16两为1斤之故.

例2计算机中常用的十六进制是逢16进1的计数制，采用数字0～9和字母A～F共16个记数符号，这些符号与十进制数的对应关系如下表：

十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

例如，用十六进制表示：E+D=1B，则A×B=

A.6E B.72 C.5F D.B0

【答案】A

4.“良马追及”问题

“良马追及”问题出自元朝杰出数学家朱世杰的《算学启蒙》一书，题曰：良马日行二百四十里，驽马日行一百五十里，驽马先行十二日，问良马何日追及之？

答：20日.

5.“盈不足术”

载于《九章算术》第七章，为我国所独创，该章第一题为：今有共买物，人出八盈三；人出七不足四.问人数、物价各几何？

答：人数为7，物价为53.算法为——

设人数为x，物价为y.每人出 a，盈b；每人出a′，不足 b′，

将题中数据代入即可得解.

这类算术题叫做“盈亏”问题，有了上面的解法就可以程序化解决该类问题，与算法一章联系密切.

6.不定方程

“百鸡”问题：今有鸡翁一，值钱五；母鸡一，值钱三；鸡雏三，值钱一.凡百钱买鸡百只.问鸡翁、母鸡、鸡雏各几何？

这是一历史名题，早在公元五世纪末，《张丘建算经》中便提出了这一问题，它是我国古代数学史上杰出的成就之一，曾经传到国外，在世界影响很大.

解答：设鸡翁、母鸡、鸡雏分别为 x、y、z只，根据题意可得：

如今我们可以运用scilab软件运行下面的程序：

其结果是：

（1）0、25、75；（2）4、18、78；（3）8、11、81；（4）12、4、84.

7.数列

（1）一般数列

南北朝张丘建始创等差数列求和解法.在《张丘建算经》中记载几个等差数列问题，如：

（1）今有女子不善织布，逐日所织的布以同数递减.初日织五尺，末日织一尺，计织三十日，问共织几何？

（2）今有女子善织布，逐日所织的布以同数递增.初日织五尺，计织三十日，共织九匹三丈，问日增几何？

解答：

这与我们教材中的等差数列两个求和公式完全等价.

例3《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为

【答案】B

（2）高级数列

宋代杰出数学家沈括的著作《梦溪笔谈》中有这样一题：

假设酒坛堆成的长方垛顶层宽为a个，长为b个；底层宽为c个，长为d个，共有n层，求酒坛总数.

解答：该题中各层酒坛个数组成一个二阶等差数列：

ab，（a+1）（b+1），（a+2）（b+2），…，cd.

而且沈括给出了求解公式：

与高阶数列有关，我们可以编制这样的试题：

例4已知数列则数列｝的和S2017=____.

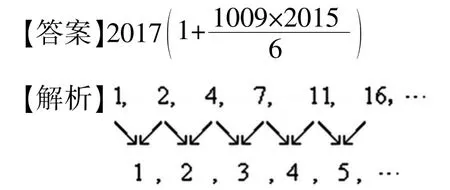
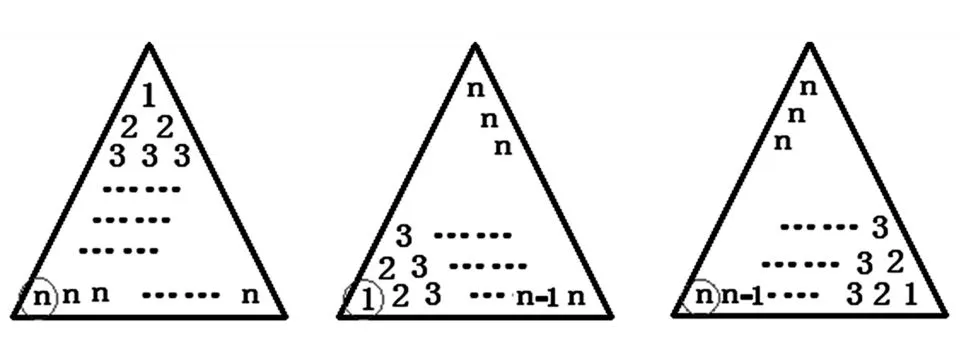
观察上面的三个三角形，相同位置的三个数之和为 2n+1，共计有个相同的位置，上述三个三角形内数字之和为三个三角形数组之和完全相等，故而一个三角形内数字之和为多么美妙的构思！

8.二项式定理

我国古代数学家最早发现二项式定理，在宋朝数学家杨辉所著的《详解九章算术》一书中记载了二项展开式的系数表，并声明“贾宪用此术”.原来，在贾宪时代，人们已将传统开方法推广到开高次方.贾宪把这种开方法称为“立成释锁法”.“释锁”形象地将开方比喻为打开一把锁；“立成”是唐宋历算家使用的一些计算常数的算表；因此，“立成释锁法”就是借助于算表进行开方的方法.这个算表就是贾宪三角，这就是为什么贾宪将其称为“开方作法本源”.这个图下面有五句话：“左斜乃积数，右斜乃隅算，中藏者皆廉.以廉乘商方，命实而除之.”前三句说明了贾宪三角的结构：最外左右斜线上的数字，分别是（a+b）n展开式中积 bn和隅算 an（n=0，1，2，3，……）的系数，中间的 2；3，3；4，6，4；……分别是展开式的各廉.后两句说明了各系数在“立成释锁法”中的应用.贾宪三角之后有造表法，即“增乘方求廉法”，并给出了求六次方各廉的细草.这是确定某次方的位数后，自下而上，随乘随加，求得各廉的方法.显然，用这种方法可以写出任意层数的贾宪三角.元朱世杰用两组并行线将贾宪三角的各数联结起来，说明它还是解决高阶等差级数求和问题的主要工具.（注：左图为贾宪三角，右图为杨辉三角）

例5如图，在由二项式系数所构成的杨辉三角形中，第____行中从左至右第14与第15个数的比为 2∶3.

【答案】34

二、与几何相关的古代数学文化内容

1.勾股定理

我国最早的数学文献《周髀算经》中记述了周公与古代数学家商高的一段对话，首先提出勾股形的问题.商高说：“故折矩，以为勾广三，股修四，径隅五.”这是勾股定理的一个特例.对勾股定理的证明，最早的形式见于公元3世纪吴国人赵爽所著《勾股圆方图注》，在这篇短文中，赵爽用割补法画了一张所谓的“弦图”（如图），其中每一个直角三角形称为“朱实”，中间的一个小正方形叫“中黄实”，以弦为边的正方形ABEF叫“弦实”.由图可知四个朱实加上一个中黄实就等于弦实，所以有下式成立：

这个证明方法通过图形的分割、移补，简单明了地解决了问题.

例 6“无字证明”（proofs without words），就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系，写出该图所验证的一个三角恒等变换公式：____.

2.圆周率

（1）徽率

而刘徽利用“割圆术”计算圆周率的方法中说：“割之弥细，所失弥少，割之又割以至不可割，则与圆合体而无所失矣”，含有极限的思想，阐明了积分学上计算长度和面积的基础.

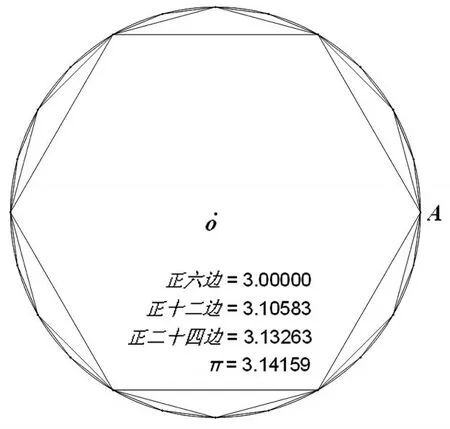
（2）祖率

我国南北朝时期杰出数学家祖冲之在世界上最早提出圆周率的两个分数表达式（约率）（密率/祖率）.

3.海伦-秦九韶公式

人们常把已知三角形三边a，b，c求其面积S的公式表示为

在人教B版教材必修五书后习题中有要求推导该公式.

（1）牟合方盖体积

（2）半球体积

证明这里不再赘述，希望同学们自己推导一下.

例7由曲线围成的图形绕y轴旋转一周所得旋转体的体积为V1，满足x2+y2≤16，x2+（y-2）2≥4，x2+（y+2）2≥4 的点（x，y）组成的图形绕y轴旋转一周所得旋转体的体积为V2，则V1与V2的大小关系为____.

【答案】相等

我们还可以将其推广到平面几何中，看下面的问题：

例8祖原理的推论：夹在两条平行线之间的两个平面封闭图形被平行于这两条直线的任意直线所截，如果截得的两条线段长度之比总为常数k，那么这两个平面图形的面积之比也为常数k；另外如图所示，椭圆可以被认为由圆x2+y2=a2作纵向压缩变换或由圆x2+y2=b2作横向拉伸变换得到的.依据上述论述我们可以推出椭圆C的面积公式为____.

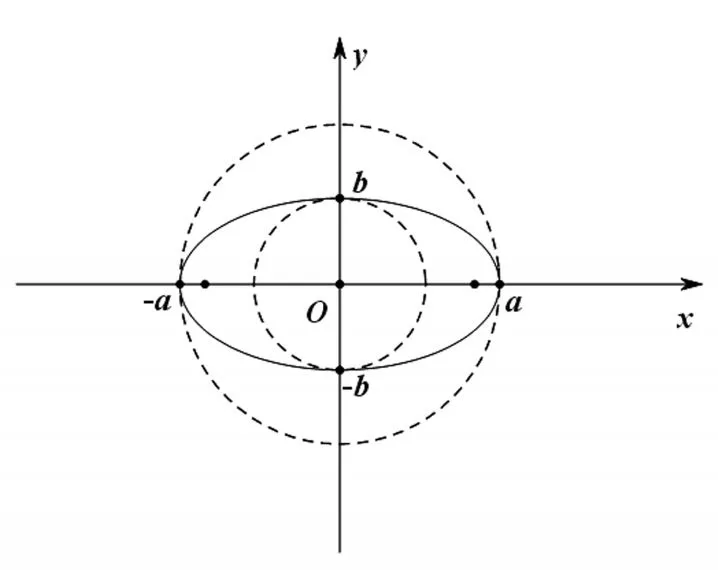
【答案】πab.

另外我国古代在《海岛算经》中还记录了大量关于物距测量问题的解决方法，如重差法、勾股测量术等，由于篇幅所限就不一一列举了，总之希望通过对本文的阅读使同学们对我国古代数学文化有一个大致的了解，在未来的试卷中遇到相关背景的问题不至于慌乱，更希望同学们喜欢上数学，为数学的进步多做贡献.

三、数学文化高考到底怎么考

正如开篇所言，高考为什么要考数学文化同学们并不关心，数学文化在高考到底考什么，通过上面的叙述我们也略知梗概，我们更关心的是数学文化在高考中到底怎样考.数学文化与教材相关知识有机融合是考试方向，耳听为虚眼见为实，下面列举出最新全国各地模考中出现的考题来给同学们提供具体的实战机会，let's go!

例9我国古代有用一首诗歌形式提出的数列问题：远望巍巍塔七层，红灯向下成倍增，共灯三百八十一，试问塔顶几盏灯？

A.5 B.4 C.3 D.2

【答案】C

例10齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹进行一场比赛，则田忌马获胜的概率为

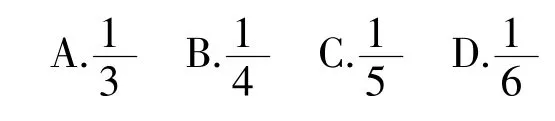
【答案】A

例11公元263年左右，我国数学家刘徽发现，当园内接正多边形的边数无限增加时，多边形面积可以无限逼近圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的程序框图，则输出的n值为____（参考数据：0.2588，sin7.5°≈0.1305）

A.12 B.24 C.48 D.96

【答案】B

例12《九章算术》是我国古代一部重要的数学著作，书中有如下问题：“今有良马与驽马发长安，至齐.齐去长安三千里，良马初日行一百九十三里，日增一十三里；驽马初日行九十七里，日减半里.良马先至齐，复还迎驽马.问几何日相逢.”其大意为：“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里，良马第一天行193里，之后每天比前一天多行13里；驽马第一天行97里，之后每天比前一天少行0.5里.良马到齐后，立刻返回去迎接驽马，多少天后良马和驽马相遇.”利用我们所学的知识，可知离开长安后第____天，两马相逢.

【答案】16.

希望老师们勤挖掘数学文化与高考结合的例子与同学们共同切磋，祝愿高三学子勤奋学习、积极思考、常总结归纳，在2017年高考中取得理想成绩！