气井井筒气液两相环雾流压降计算新方法

刘通王世泽郭新江潘国华陈海龙伍洲

1.中国石化西南油气分公司博士后科研工作站；2.中国石化西南油气分公司石油工程技术研究院；3.中国石油新疆油田分公司勘探开发研究院；4.中国石化西南油气分公司川西采气厂

气井井筒气液两相环雾流压降计算新方法

刘通1，2王世泽2郭新江2潘国华3陈海龙2伍洲4

1.中国石化西南油气分公司博士后科研工作站；2.中国石化西南油气分公司石油工程技术研究院；3.中国石油新疆油田分公司勘探开发研究院；4.中国石化西南油气分公司川西采气厂

气液两相环雾流是气井生产中最常见的流型之一，正确预测其井筒压降是气井节点系统分析、生产动态预测的重要基础。从环雾流气芯-液膜分相流结构出发，建立了环雾流压力梯度方程；其中持液率计算综合考虑了液膜及液滴的影响，通过引入Henstock & Hanratty无因次液膜厚度关系式，导出了液膜厚度计算显式方程，基于液滴沉降与液膜雾化的动态平衡，导出了适用于气井低液相雷诺数条件的液滴夹带率关系式；摩阻计算考虑了液膜与管壁的剪切应力，最终采用龙格库塔法迭代求解井筒压力。利用国内外91井次气井测压数据评价表明，新模型提高了凝析气井和产水气井井筒环雾流压降预测准确度，优于传统的均匀流模型和分相流模型，而且能够获得液滴夹带率、液膜厚度等特性参数，为油气田开发提供技术理论支持。

气井；井筒；压降；环雾流；液滴；液膜；分相流

在高气液比气井或凝析气井生产过程中，井筒主要以环雾流型为主，当采用小油管生产或气举排液时，井筒中也会出现环雾流，环雾流是气井中最为常见的流型之一［1］。它表现为气流夹带液滴从油管中部快速通过、液膜附着管壁呈环状上升的现象。正确预测井筒气液两相环雾流压降对气井节点系统分析、生产动态预测、开发方案优化至关重要。

早年的学者将环雾流简化为一种气液间无滑脱的均匀流动，认为气液不存在速度差［1-3］。这类方法忽视了液膜的存在以及液膜的滑脱，低估了环雾流的真实压力损耗。后来有学者将环雾流的气芯与液膜进行区别对待，并考虑了气芯中液滴的夹带、管壁处液膜的滑脱以及气芯与液膜间的摩阻，建立了分相流模型［4-5］。这类方法不仅能预测压降，还能获得液滴夹带率、液膜厚度等一系列特性参数，因此被称为机理模型［6-9］。然而近年来有些学者研究发现，这类模型在计算液膜厚度时需要求解一个复杂的包含3个封闭关系式的隐式方程，常常产生异常解，降低模型精度［10-11］。

为此建立了新的气井井筒气液两相环雾流压降模型，首先从环雾流气芯-液膜分相流结构特征出发，建立了压力梯度方程，随后引入Henstock &Hanratty无因次液膜厚度关系式，结合分相流几何关系，将液膜厚度以及持液率的计算方程简化为显式方程，并自行推导了适用于气井低液相雷诺数条件的液滴夹带率关系式，摩阻计算考虑了液膜与管壁的剪切应力，采用龙格库塔法求解井筒压力；最后利用公开文献数据对模型进行了评价，对液滴夹带率和无因次液膜厚度进行了预测，并对传统模型性能不佳的原因进行了讨论。

1 压力梯度方程

Pressure gradient equation

将油管中的流动视为沿井深L的一维流动，并规定流动方向为L的正方向。当流型呈现环雾流时，中心气流夹带液滴快速上升，液膜呈环状附着管壁，其微元段结构以及过流断面如图1所示。

根据动量守恒方程，总压力梯度由流体重力、流体与管壁的摩阻和流体动能损失组成

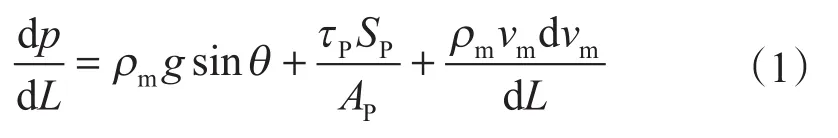
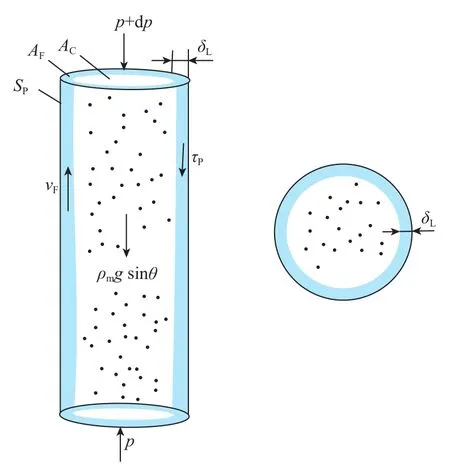
图1 油管中环雾流Fig.1 Annular-mist flow in the oil tube

式中，p为压力，Pa；L为井深，m；dp/dL为沿井深方向的压力梯度，Pa/m；ρg、ρL、ρm分别为气相、液相、气液混合物密度，kg/m3；g为重力加速度，m/s2；θ为管斜角（油管与水平面的夹角），°；τp为混合物与管壁的剪切应力，Pa；SP为油管湿周，m；AP为油管内截面积，m2；vm为气液混合物流动速度，m/s；HL为油管截面持液率。

一般情况下，流体动能损失远远小于流体重力与摩阻的损失，因此压力梯度计算的核心问题是确定油管截面持液率HL和剪切应力τp。

2 持液率计算

Liquid holdup calculation

2.1 持液率

Liquid holdup

持液率定义为过流断面上液相面积占总过流面积的份额。对于环雾流，持液率来源于气芯中液滴与管壁处液膜之和

式中，HLC为气芯持液率；AC、AF分别为气芯截面积、液膜截面积，m2。

气芯持液率的大小取决于液滴含量，而液滴含量由液滴夹带率FE表征，定义为液滴液量占总液量的份额［4］。考虑到气芯流速高，气液滑脱可忽略，于是气芯持液率为

式中，FE为液滴夹带率；vsg、vsL分别为气相表观流速、液相表观流速，m/s。

油管湿周、油管内截面积、气芯截面积和液膜截面积满足以下几何关系

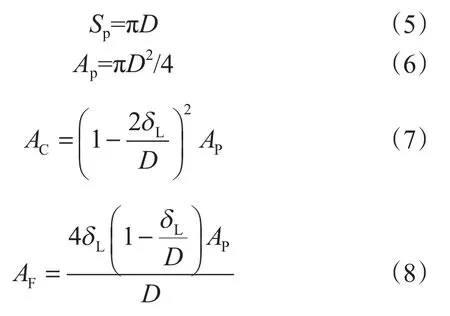
式中，δL为液膜厚度，m；D为油管内径，m。

联立式（3）～式（8），得持液率表达式为

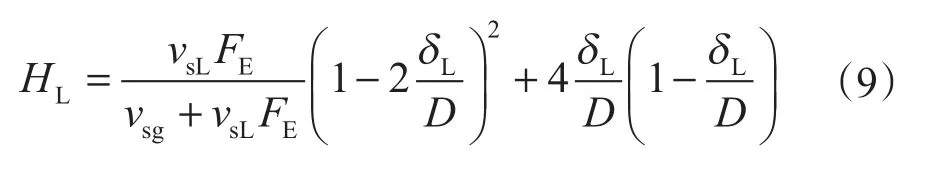
由式（9）可知，环雾流持液率是关于液滴夹带率FE和液膜厚度δL的函数。当FE接近0时，液膜占主导；当FE接近1时，液滴占主导，接近雾流。

2.2 液膜厚度

Liquid membrane thickness

Henstock & Hanratty基于大量的环雾流实验，发现液膜厚度与气液密度、气液黏度以及气液流态有关，导出了适用于液相雷诺数20～15 100、油管内径12.8～63.5 mm范围的垂直上升环雾流无因次液膜厚度计算式为［12］

式中，Reg、ReLF分别为气芯雷诺数、液膜雷诺数；μg、μL分别为气相黏度、液相黏度，Pa·s；vF为液膜流速，m/s；DHF为液膜水力直径，m。

根据几何关系，液膜水力直径及流速分别为

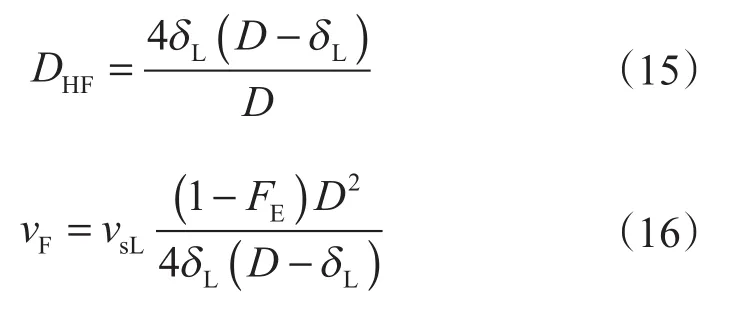
将式（15）、式（16）代入式（12），消除液膜厚度项后，简化得到

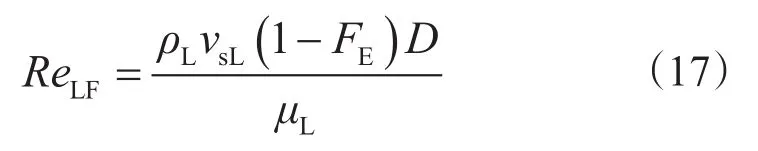
关于液膜厚度的隐式方程式（10）转换为了一个显式方程。

2.3 液滴夹带率

Droplet entrainment rate

环雾流场中时刻发生着液滴的沉降与液膜的雾化。液滴沉降率是指单位时间、单位面积上沉降的液滴质量，主要受液滴质量浓度影响，浓度越大，沉降越快［13］

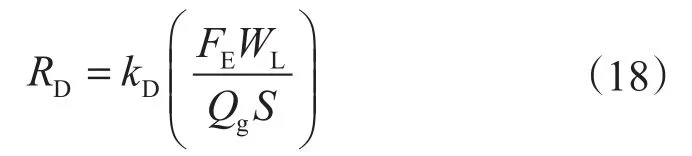
式中，RD为液滴沉降率，kg/（m2·s）；kD为沉降系数，m/s；WL为液体质量流量，kg/s；Qg为气体体积流量，m3/s；S为液滴速度与气流速之比。

液膜雾化率是指单位时间、单位面积上雾化的液膜量，主要与气液流量、密度、管径有关，气量越大、液量越大，雾化越快；液量低于某临界液量WFC时，液膜扰动减弱，不足以产生液滴，表达式为［14-15］

式中，RA为液膜雾化率，kg/（m2·s）；kA为无因次雾化系数；σL为气液界面张力，N/m；WFC为临界液膜质量流量，kg/s。

当液滴沉降率与液膜雾化率相等时，液滴夹带率达动态平衡，则

式中，FE，max定义为极限液滴夹带率，受临界液量WFC控制。

忽略液滴与气流之间的滑脱时S=1；根据Pan &Hanratty的研究，kAvsg/（4kD）近似等于常数6×10–5；极限液滴夹带率FE，max采用Al-Sarkhi关系式计算，适用于低液相雷诺数范围（ReL＞450），更接近高气液比气井条件［15-16］

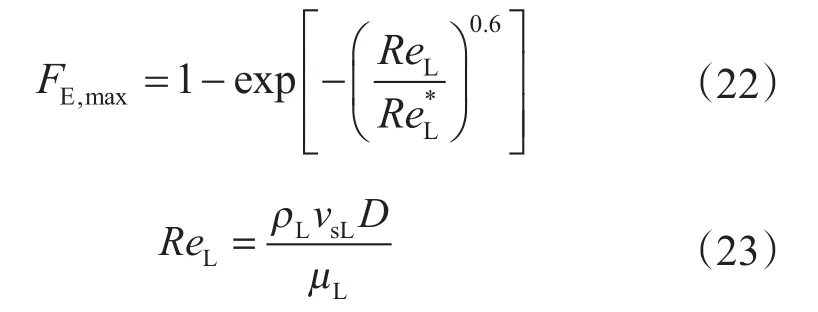
式中，ReL为液相雷诺数；为实验回归的临界液相雷诺数，取值1 400。

联立式（20）、式（22）得液滴夹带率计算式为

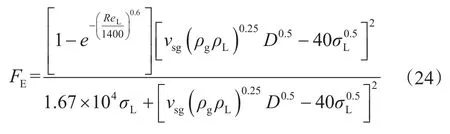
3 摩阻计算

Friction calculations

环雾流液膜附着管壁，摩阻压降来源于液膜与管壁间的剪切应力为

其中液膜与管壁间的摩阻系数按Moody图版计算得到［17］

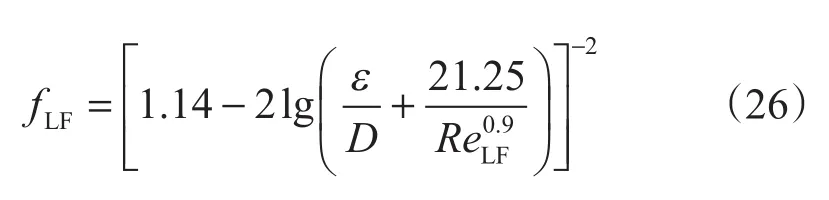
式中，fLF为液膜与管壁间的Moody摩阻系数；ε为管壁绝对粗糙度，可取0.015 24 mm。

若液膜流动处于层流（ReLF＜2 300），则摩阻系数为

4 井筒压力计算方法

Wellbore pressure calculation methods

综合式（2）、（5）、（6）、（9）、（10）、（23）、（24）可以计算环雾流总压力梯度方程式（1），其中式（1）右函数包含了流体物性、运动参数及其有关的无因次变量。将其处理为常微方程的初值问题，即

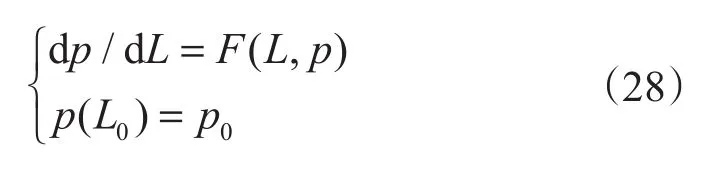
以井口深度L0、井口压力p0为初值条件，根据压力梯度式（1），假设温度沿井深呈线性分布，按龙格库塔法依次求解井筒各深度的压力，气液物性参数计算参照文献［17］［17-18］。

5 验证及讨论

Verification and discussion

收集了加拿大能源保护委员会公布的94口凝析气井测压数据，根据组分模型分析结果，有55口测压井井筒呈现两相流，且产气量均高于携液临界气量，流型呈现环雾流，因此利用这55口井的测压数据对新模型进行评价［19］。其井口压力3.1～19.7 MPa，井底压力4.5～31.6 MPa，产气量（2.61～77.59）×104m3/d，产液量2.3～263.9 m3/d，含水率0～0.41，液相雷诺数531～10 240，油管下深范围为1 121～3680 m，气液比1 070～33 138 m3/m3，油管内径50.7～76.0 mm，气体相对密度0.63～0.84，油相对密度0.58～0.93，水相对密度1.02。参评模型包括新模型、1963年Duns & Ros均匀流模型（简写为D-R）、1991年Alves分相流模型、2007年Hasan & Kabir均匀流模型（简写为H-K）。

评价指标采用文献［18］定义的6项误差指标E1～E6以及一个相对性能系数RPF。其中E1、E4反映了误差的整体偏差、E2、E5反映了误差的幅度大小、E3、E6反映了误差的离散程度，而RPF范围在0～6，其值越小说明模型综合性能越优。基于公开文献55口凝析气井测压数据的评价结果见表1。

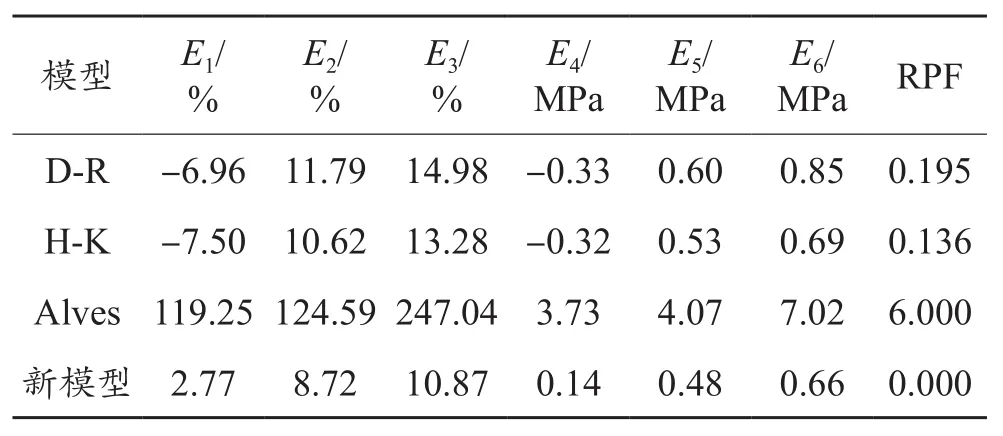
表1 环雾流模型评价结果Table 1 Evaluation results of annular-mist flow model

由表1可知，新模型RPF指标为0，且各项误差均最小，性能最佳；D-R、H-K两种均匀流模型综合性能其次，但由于忽略了液膜的滑脱，E1、E4指标偏低，低估了环雾流气井的真实压降；Alves分相流模型误差较大，这是由于其动量组合隐式方程求解液膜厚度时存在异常解所致，所计算的无因次液膜厚度大于Wallis所提到的5%的极限值，此类异常解多达22组，这与Hasan & Kabir、Peter & Acuna的结论一致［1、10］。

利用新模型对这55口环雾流气井的井口、井底无因次液膜厚度、液滴夹带率等参数作出预测，如图2、图3所示。结果表明，无因次液膜厚度范围在0.06%～2.52%，液滴夹带率范围0～0.91；井口液膜厚度普遍大于井底条件，这是由于凝析气井反凝析现象所致；井口液滴夹带率普遍高于井底条件，这是由于井口高流速对液膜的剪切破碎更加剧烈所致。

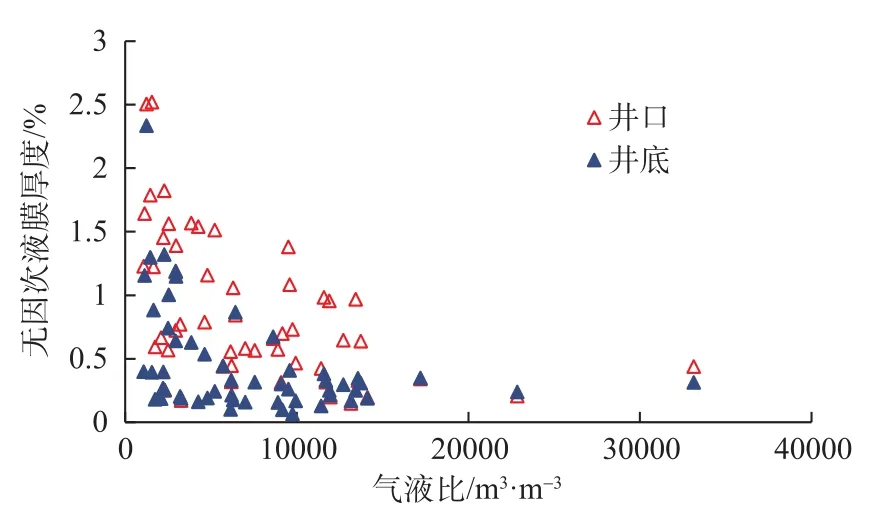
图2 环雾流无因次液膜厚度预测Fig.2 Dimensionless liquid membrane thickness prediction for the annular mist flow

图3 环雾流液滴夹带率预测Fig.3 Droplet entrainment rate prediction for the annular-mist flow

为了进一步验证模型适用性，收集了来自川西中浅层致密砂岩气藏、川西深层须家河组气藏产水气井2010—2015年120井次测压数据。其中有36井次测压数据符合环雾流生产特征：气量高于李闽携液临界气量，满足环雾流形成条件（如图4所示）［20］；双波纹卡片曲线平滑，井口出液连续；测压数据无积液液位显示。具体数据范围：井口压力为0.5～27.7 MPa，井底压力为1.2～34.1 MPa，产气量为（0.90～6.07）×104m3/d，产液量为0.1～72 m3/d，含水率为100%，油管下深为704～4 400 m，气液比为611～141 010 m3/m3，油管内径为62.0～76.0 mm，气体相对密度为0.57～0.65，水相对密度为1.02。

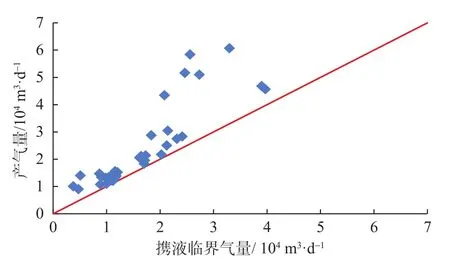
图4 产气量与携液临界气量的对比Fig.4 Comparison of gas production and critical liquid carrying gas production

同理利用文献［18］定义的6项误差指标E1～E6以及相对性能系数RPF对4个环雾流模型进行评价，基于川西气田36井次产水气井测压数据结果见表2。与前文凝析气井评价结果相似，新模型性能仍然最优，RPF指标为0，且各项误差均最小；D-R、H-K两种模型依然低估了环雾流气井压降；而Alves分相流模型则出现了14组异常解，性能不佳。

表2 环雾流模型评价结果Table 2 Evaluation results of the annular mist flow model

6 结论

Conclusions

（1）建立了新的气井井筒气液两相环雾流压降模型，综合考虑了液膜与液滴对持液率的贡献，液膜厚度基于Henstock & Hanratty关系式与分相流几何关系推导得到，液滴夹带率基于液滴沉降与液膜雾化的动态平衡以及Al-Sarkhi关系式推导得到，摩阻计算考虑了液膜与管壁的摩擦。

（2）国内外91井次测压数据评价表明，新模型适用于气量高于携液临界气量、流型呈现环雾流、井深小于4 400 m、井口压力小于27.7 MPa、油管内径50.7～76.0 mm条件下的凝析气井或产水气井井筒压降预测。

（3）传统均匀流模型由于忽略了液膜的滑脱，低估了环雾流压降；传统分相流模型由于其动量组合隐式方程求解液膜厚度时存在异常解，降低了模型精度。

参考文献：

［1］HASAN A R,KABIR C S.A simple model for annular two-phase flow in wellbores ［J］.SPE Production &Operations,2007,22（2）: 168-175.

［2］DUNS H J,ROS N C J.Vertical flow of gas and liquid mixtures in wells ［C］.Frankfurt: Sixth World Petroleum Congress,1963.

［3］AZIZ K,GOVIER G W,FOGARASI M.Pressure drop in wells producing oil and gas ［J］.Journal of Canadian Petroleum Technology,1972,11: 38-47.

［4］WALLIS G B.One dimensional two-phase flow ［M］.New York: McGraw-Hill Book Co.Inc.,1969.

［5］ALVES L M,CAOTANO E F,MINAML K,SHOHAM O.Modeling annular flow behavior for gas wells ［J］.SPE Production Engineering,1991,6（4）: 435-440.

［6］ANSARI A M,SYLVESTER N D,SARICA C,SHOHAM O,BRILL J P.A comprehensive mechanistic model for upward two-phase flow in wellbores ［J］.SPE Production& Facilities,1994,9（2）: 143-151.

［7］KAYA A S,SARICA C,BRILL J P.Mechanistic modeling of two-phase flow in deviated wells ［J］.SPE Production& Facilities,2001,16（3）: 156-165.

［8］刘晓娟，胥元刚，彭缓缓，穆谦益，崔凯，曹小娟.倾斜井筒气液两相流的模型化方法［J］.石油钻采工艺，2009，31（3）：52-57.LIU Xiaojuan,XU Yuangang,PENG Huanhuan,MU Qianyi,CUI Kai,CAO Xiaojuan.Mechanistic modeling of two-phase flow in deviated wells ［J］.Oil Drilling &Production Technology,2009,31（3）: 52-57.

［9］李波，王军磊，宁波，苏海洋.气井井筒温度、压力与积液综合预测模型［J］.石油钻采工艺，2014，36（4）：64-70.LI Bo,WANG Junlei,NING Bo,SU Haiyang.A comprehensive prediction model of wellbore temperature,pressure and accumulated liquid for gas wells ［J］.Oil Drilling & Production Technology,2014,36（4）: 64-70.

［10］PETER P,ACUNA J A.Implementing mechanistic pressure drop correlations in geothermal wellbore simulators ［C］.Bali: World Geothermal Congress,2010.

［11］刘通.产液气井两相流机理模型研究［D］.成都：西南石油大学，2014.LIU Tong.Mechanistic model for twophase flow in liquidcut gas wells ［D］.Chengdu: PhD Dissertation of Southwest Petroleum University,2014.

［12］HENSTOCK W H,HANRATTY T J.The interfacial drag and the height of the wall layer in annular flows［J］.AIChE Journal,1976,22（6）: 990-1000.

［13］HANRATTY T J,WOODS B D,ILIOPOULOS I,PAN L.The roles of interfacial stability and particle dynamics in multiphase flows: a personal viewpoint ［J］.International Journal of Multiphase Flow,2000,26（2）:169-190.

［14］SCHADEL S A,HANRATTY T J.Interpretation of atomization rates of the liquid film in gas liquid annular flow ［J］.International Journal of Multiphase Flow,1989,15（6）: 893-900.

［15］PAN L,HANRATTY T J.Correlation of entrainment for annular flow in vertical pipes ［J］.International Journal of Multiphase Flow,2002,28（3）: 363-384.

［16］AL-SARKHI A,SARICA C,QURESHI B.Modeling of droplet entrainment in co-current annular two-phase flow: a new approach ［J］.International Journal of Multiphase Flow,2012,39（1）: 21-28.

［17］BEGGS H D,BRILL J P.A study of two phase flow in inclined pipes ［J］.Journal of Petroleum Technology,1973,25（5）: 607-617.

［18］李颖川，朱家富，秦勇.排水采气井油管和环空两相流压降优化模型［J］.石油学报，1999，20（2）：87-91.LI Yingchuan,ZHU Jiafu,QIN Yong.An optimal model for two-phase flow in tubing and annulus of gas wells［J］.Acta Petrolei Sinica,1999,20（2）: 87-91.

［19］GOVIER G W,FOGARASI M.Pressure drop in wells producing gas and condensate ［J］.Journal of Canadian Petroleum Technology,1975,14（4）: 28-41.

［20］李闽，郭平，谭光天.气井携液新观点［J］.石油勘探与开发，2001，28（5）：105-106.LI Min,GUO Ping,TAN Guangtian.New look on removing liquids from gas wells ［J］.Petroleum Exploration and Development,2001,28（5）: 105-106.

（修改稿收到日期 2017-01-15）

〔编辑 李春燕〕

New calculation method of gas-liquid two phase annular-mist flow pressure drop of wellbores in gas wells

LIU Tong1,2,WANG Shize2,GUO Xinjiang2,PAN Guohua3,CHEN Hailong2, WU Zhou4
1.Post-Doctoral Research Station of Southwest Oil & Gas Branch,SINOPEC,Chengdu610041,Sichuan,China;
2.Petroleum Engineering Technology Institute,Southwest Oil & Gas Branch,SINOPEC,Deyang618000,Sichuan,China;
3.Research Institute of Exploration and Development,Xinjiang Oilfield Company,CNPC,Karamay834000,Xinjiang,China;
4.Chuanxi Gas Production Plant,Southwest Oil & Gas Branch,SINOPEC,Deyang618000,Sichuan,China

Gas-liquid two phase annular-mist flow is one of the most common flow patterns in the production of gas wells and the important foundation of nodal system analysis and production performance prediction for the gas wells is correct prediction of the wellbore pressure drop.The pressure gradient equation for the annular-mist flow was established from the air core-liquid membrane separated phase flow structure of annular-mist flow.Therein,the contributions of liquid membranes and droplets were comprehensively considered in the liquid holdup calculation.By inducing Henstock & Hanratty dimensionless liquid membrane thickness relation formula,the explicit equation for the liquid membrane thickness calculation was derived.Based on the dynamic equilibrium of droplet settling and liquid membrane atomization,the droplet entrainment relation formula of low liquid phase Reynolds numbers applicable to gas wells was also derived.Besides,the shear stress of liquid membranes and tube walls was considered in the friction calculation and the wellbore pressure was finally solved by using Runge-Kutta iteration.The pressure test data evaluation for 91 gas wells at home and abroad shows that the new model has improved the prediction accuracy of the wellbore annular-mist flow pressure drop in the condensate gas wellsand water-yielding gas wells and is better than the traditional uniform phase flow model and divided phase flow model.Moreover,the characteristic parameters of droplet entrainment rate and liquid membrane thickness and etc.can also be obtained.

gas wells; wellbore; pressure drop; annular-mist flow; droplet; liquid membrane; divided phase flow

刘通，王世泽，郭新江，潘国华，陈海龙，伍洲.气井井筒气液两相环雾流压降计算新方法［J］.石油钻采工艺，2017，39（3）：328-333.

TE37

：A

1000–7393（2017 ）03–0328–06DOI:10.13639/j.odpt.2017.03.014

: LIU Tong,WANG Shize,GUO Xinjiang,PAN Guohua,CHEN Hailong,WU Zhou.New calculation method of gas-liquid two phase annular-mist flow pressure drop of wellbores in gas wells［J］.Oil Drilling & Production Technology,2017,39(3): 328-333.

国家科技重大专项“超深层高含硫气田水平井高产稳产工艺技术研究” (编号：2016ZX05017-005-003)。

刘通（1986-），2014年毕业于西南石油大学获博士学位，现主要从事油气井多相流理论以及采气工程技术研究工作。通讯地址：（618000）四川省德阳市龙泉山北路298号。E-mail: liutong697@126.com