崖城气田含水汽凝析气偏差因子预测方法评价

熊钰李佩斯邓丹莫军李玮李跃林

1.西南石油大学油气藏地质及开发工程国家重点实验室；2.辽河油田分公司兴隆台采油厂；3.中海石油湛江分公司生产部

崖城气田含水汽凝析气偏差因子预测方法评价

熊钰1李佩斯1邓丹1莫军1李玮2李跃林3

1.西南石油大学油气藏地质及开发工程国家重点实验室；2.辽河油田分公司兴隆台采油厂；3.中海石油湛江分公司生产部

天然气偏差因子是气藏工程计算中一项相当重要的参数，多采用经验公式求取。由于不同计算模型使用范围和精度不同，并且计算凝析气偏差因子的常规方法通常忽略含水的影响，导致偏差因子的计算误差较大。针对以上难点，分别采用不同的计算方法，结合WA、Casey等校正模型，计算含水汽凝析气的偏差因子。通过比较偏差因子的计算值与实验值，评价HY、DBR及DAK三种不同模型在计算含水汽凝析气偏差因子时的适用性。研究表明：在含水汽凝析气的偏差因子计算中，使用校正模型修正后的偏差因子误差明显减小，而随着对比压力pr的取值不同，3种方法的精度有所不同。当0≤pr≤3.87时，HY、DBR及DAK等三种方法的计算精度相似；当4.84≤pr≤6.56时，采用HY或DAK方法的精度较高；而当3.87≤pr≤4.84和6.56≤pr≤7.59时，采用DPR方法的精度更高。

含水汽凝析气；偏差因子；计算方法；崖城气田

天然气偏差因子的计算模型较多，各种模型的适应条件不同［1-2］，往往非烃类（如CO2、H2S、H2O等）的存在会影响各种模型的适用条件，因此在计算天然气偏差因子时，常常需要考虑到这些非烃类因子的影响，然而常规天然气偏差因子的计算模型中较多的是分析CO2、H2S对天然气偏差因子计算的影响，对含水汽凝析气偏差因子的计算研究甚少，因此对于含水汽凝析气偏差因子的计算模型的适应性不清。笔者以实验数据为基准，测试不同压力下凝析气组成及偏差因子，并采用HY、DAK和DPR等模型结合校正方法计算含水汽凝析气藏的偏差因子，评价出各种计算方法在含水汽情况下不同压力时的适应性。

1 实验测试

Experimental test

1.1 不同压力下凝析气组成测试

Test on the compositions of gas condensate under different pressure

参照SY/T 0529—93天然气组分分析标准，对崖城气田凝析气进行了常规组分分析，同时参照SY/T 7507—1997天然气含水量测定标准，测试了不同压力下凝析气的水组分组成，测试结果见表1。

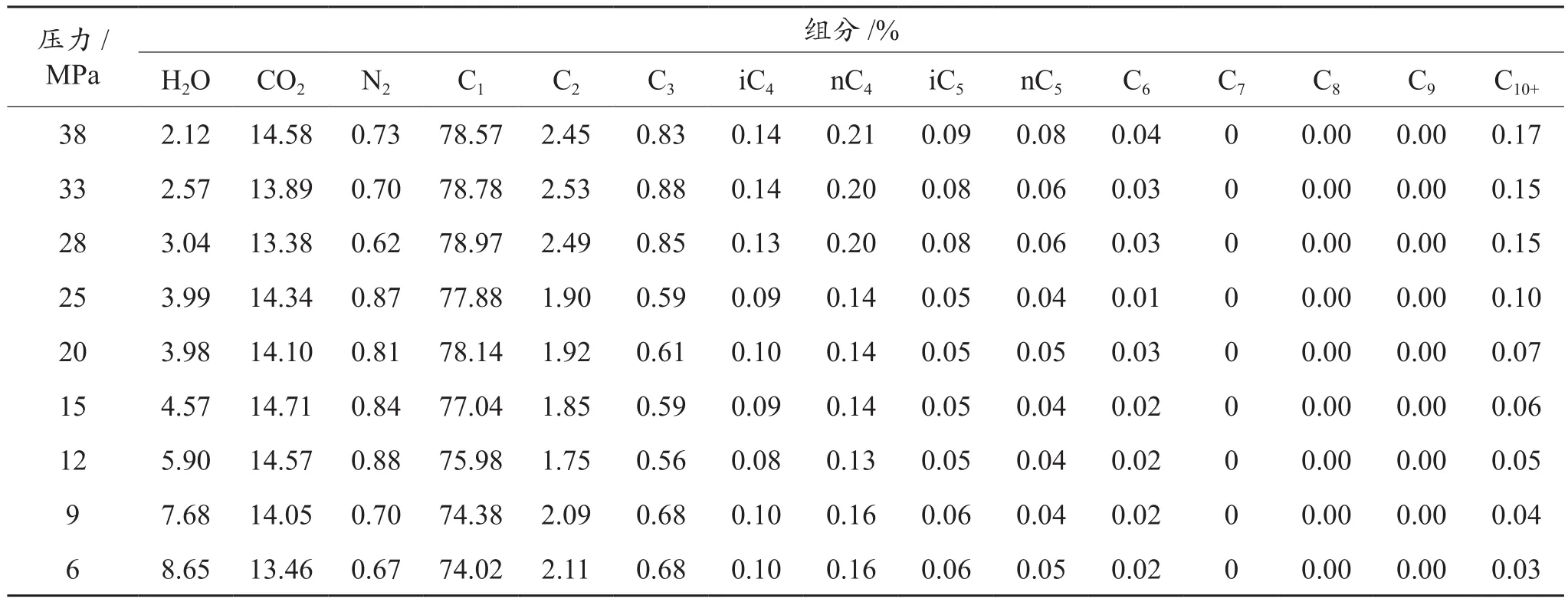
表1 不同压力下凝析气组成测试Table 1 Test on the compositions of gas condensate under different pressure

1.2 不同压力下凝析气偏差因子测试

Test on the Z-factor of gas condensate under different pressure

按照SY/T 5543—2002《凝析气藏流体物性分析方法》，对崖城气田含水凝析气样进行了偏差系数测试。测试基本步骤为：先将天然气恒温恒压到实验所要求的压力温度下测量气样体积，然后将天然气放到室温室压下再测量其体积，最后用气体状态方程计算出偏差系数。测试装置如图1所示。计算公式如下

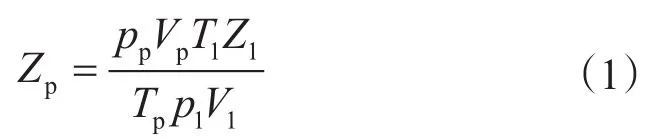
式中，Zp为配样条件下气体的偏差系数；pp为配样压力的数值（绝对），MPa；Vp为高压气体的体积的数值（由泵读数差经校正求出），cm3；Tp为配样温度的数值，K；p1为大气压力，MPa；T1为室内温度，K；V1为室温、大气压下气体的体积，cm3；Z1为室温、大气压下的气体偏差系数，一般可近似取值1。

图1 凝析气在高压下的体积测试简图Fig.1 Schematic map of volume test on gas condensate under high pressure

使用崖城气田气样（组分组成见表1）分别测试了在176 ℃温度条件下、压力2.35～38 MPa范围内的气体偏差系数， 测试结果见图2。

图2 不同压力下偏差因子的计算结果Fig.2 Calculated Z-factor under different pressure

2 偏差因子计算及其校正模型

Z-factor calculation and its correction model

2.1 偏差因子计算模型

Z-factor calculation model

2.1.1 HY方法［3］Hall-Yarborough方法发表于1973年，是以Starling-Carnahan状态方程为基础，通过拟合Standing-Katz图版数据而得，其适用范围为1.2≤Tpr≤3.0，0≤ppr≤24，其表达式为

式中，ppr为拟对比压力，无量纲；Tpr为拟对比温度，无量纲；ρr为对比密度，无量纲。

2.1.2 DPR方法［4］该模型是由Dranchuk、Purvis和Robinson于1974年根据Starling-Carnahan修正的BWR状态方程拟合Standing-Katz图版得到的，其适用范围为1.0≤Tpr≤3.0，0.1≤ppr≤24，其表达式为

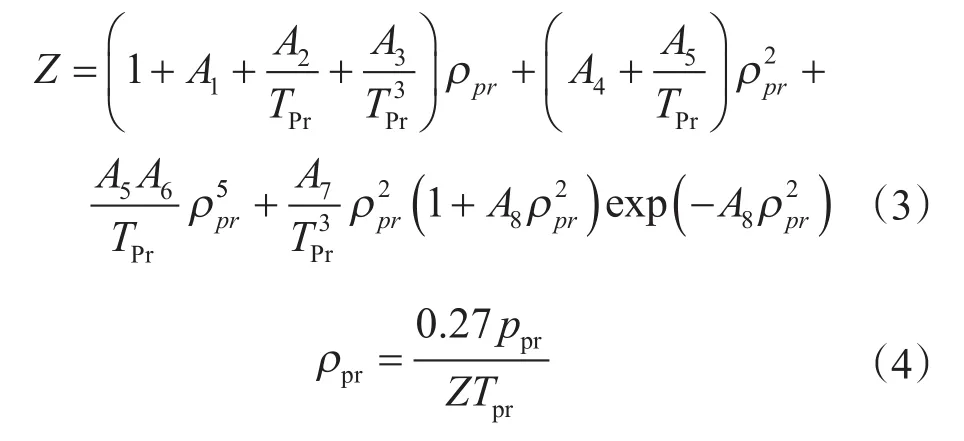
式中，ρpr为拟对比密度。

2.1.3 DAK方法［5］该模型是由Dranchuk、Abu和Kassem于1975年运用Starling-Carnahan 状态方程拟合Standing-Katz图版得到的，其适用范围为1.0≤Tpr≤3.0，0.2≤ppr≤3.0，其表达式为

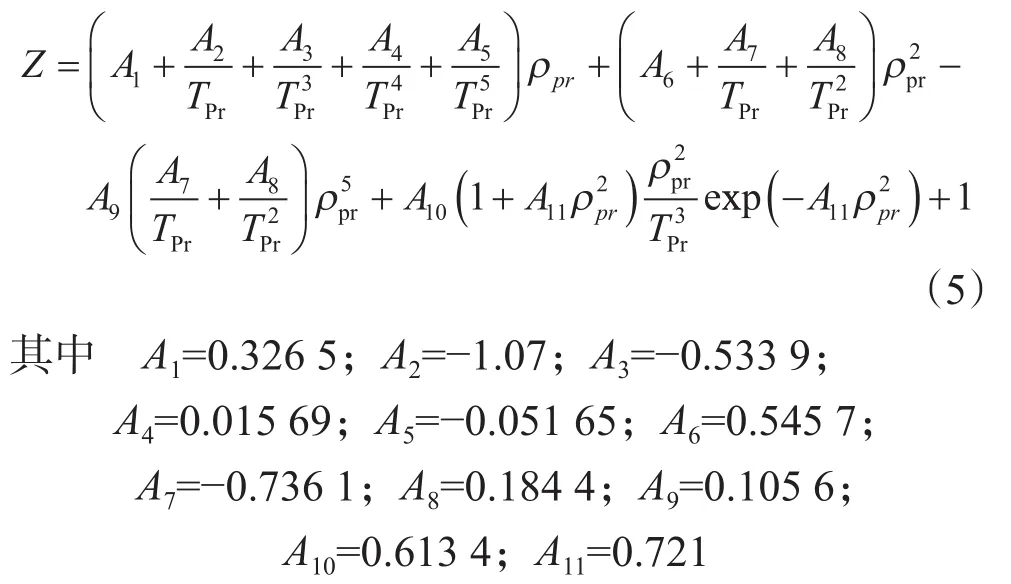
2.2 偏差因子校正方法

Z-factor correction method

目前采用两参数压缩因子法来考虑实际气体的状态变化，即认为Z值是对比压力pr和对比温度Tr两个对比参数的函数［6］，即Z=Z（pr，Tr），其中

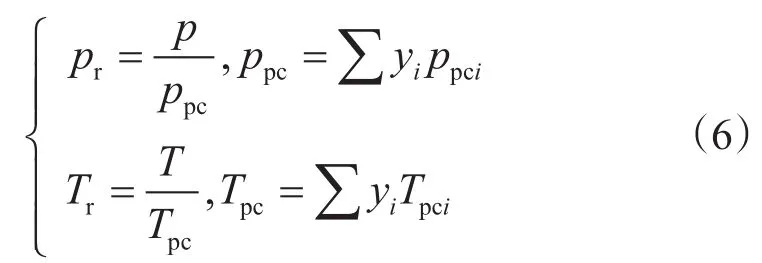
式中，p、T为气体的压力和温度；ppc、Tpc为该气体的临界压力和临界温度。

气体中如果含有非烃类组分如CO2或H2O，会改变气体的临界参数，而临界参数的改变会影响对比参数，从而影响天然气的偏差因子，因此必须对其进行相应的校正，即对偏差因子的校正转变为对临界参数的校正。

2.2.1 由CO2和N2影响的非烃校正 由于CO2、N2对拟临界参数ppc、Tpc的影响，从而影响偏差因子，利用韦切尔（Wichert）和阿齐兹（Aziz）提出修正公式［7］，减小CO2、N2对偏差因子的影响，此公式适用温度范围为4.4～300 ℃，压力范围1.06～48.43 MPa，CO2摩尔分数0～54.56%，H2S摩尔分数0～73.85%，其公式如下

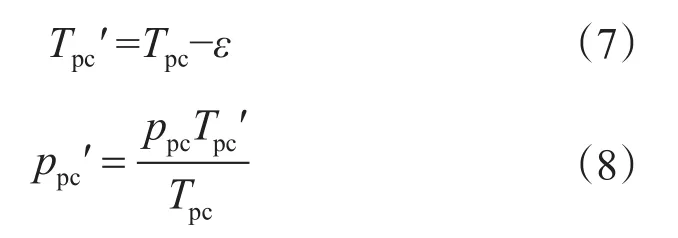
式中，A为气体混合物中CO2的总摩尔分数，小数；yN2为气体混合物中N2的摩尔分数，小数。

2.2.2 水蒸气影响校正［8］不仅非烃气体对拟临界参数ppc、Tpc产生了影响，水蒸气的存在也会影响拟临界参数ppc、Tpc，所以在对含CO2和N2非烃气体临界参数进行校正后，需再次对由水蒸气影响的临界参数进行第2次校正。通过校正拟临界性质可得到拟对比性质，这些对比性质大多数是由经验得到的，或是考虑它比忽略它得到更好的结果时才可能加以考虑。对水蒸气的拟临界性质的校正如下

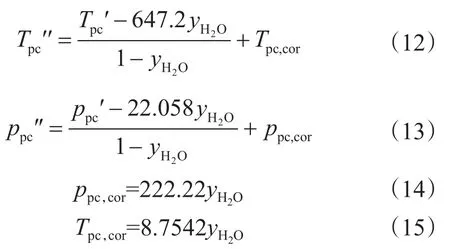
式中，ppc′为由Wichert-Aziz方法校正后的临界压力；Tpc′为由Wichert-Aziz方法校正后的临界温度；yH2O为气体中H2O组分摩尔分数，小数；yN2为气体中H2O组分摩尔分数，小数。

3 实例分析

Case study

利用表1中的数据，在HY、DPR、DAK计算模型及WA、Casey 校正模型的基础上，使用3种方法预测偏差因子：（1）未校正模型；（2）非烃校正；（3）Casey校正。未校正时计算结果见图3，校正CO2和N2后计算结果见图4，校正H2O后计算结果见图5。

图3 不同模型修正前偏差因子计算结果Fig.3 Calculated Z-factor before and after being corrected by different models

从图3可以看出，HY与DAK方法预测值几乎一致，但整体上与实测值误差较大，且误差随着压力的增大而增大；当压力p在0～20 MPa之间时，即0≤pr≤3.87时，DPR方法预测的结果与前两种方法一致，而当压力p在20～38 MPa之间时，即当3.87≤pr≤7.60时，DPR方法预测更为准确。

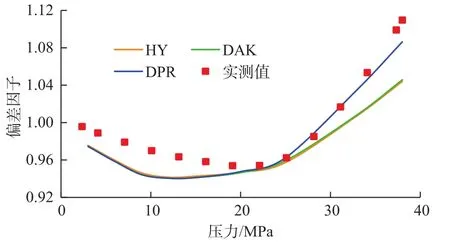
图4 非烃校正后偏差因子计算结果Fig.4 Calculated Z-factor after non-hydrocarbon correction

从图4可以看出，校正CO2及N2后，当压力p在20～38 MPa时，即在3.87≤pr≤7.60压力范围内，3种模型预测精度有了很大的提高，DPR方法的预测值与实测值的拟合程度很高；但当压力p在0～20 MPa之间时，即在0≤pr≤3.87压力范围内，仍然存在很大的误差。

图5 水蒸气影响校正后偏差因子计算结果Fig.5 Calculated Z-factor after steam influence correction

从图5可以看出，经过Casey模型校正H2O的影响后，3种计算模型预测精度均有了很大的提高；当压力p在0～20 MPa之间时，即在0≤pr≤3.87压力范围内，3种计算模型的精度差不多；当压力p在20～25 MPa与33～38 MPa之间时，即在3.87≤pr≤4.84和6.56≤pr≤7.59压力范围内，DPR的计算精度最高，误差最小；而当压力p在25～28 MPa之间时，即在4.84≤pr≤6.56范围内，HY及DAK模型拟合精度较高。

4 结论

Conclusions

（1）计算含水凝析气偏差系数时必须对临界参数进行校正，否则预测结果低于实验测试结果。经过WA模型及Casey模型校正后，DPR方法计算得到的结果与实验值趋势大体一致，其预测精度较高。

（2）通过实验与计算结果对比发现，不同计算模型的适用范围也不同：当4.84≤pr≤6.56时，应采用HY及DAK方法计算含水凝析气偏差因子；当3.87≤pr≤4.84或6.56≤pr≤7.59时，应采用DPR方法计算含水凝析气偏差因子。

References:

［1］阳建平，肖香姣，张峰，王海应.几种天然气偏差因子计算方法的适用性评价［J］.天然气地球科学，2007，18（1）：154-157.YANG Jianping,XIAO Xiangjiao,ZHANG Feng,WANG Haiying.Applicability estimation of four methods of calculating the deviation factor of natural gas ［J］.Natural Gas Geoscience,2007,18（1）: 154-157.

［2］陈亮，孙雷.CO2气藏偏差因子计算模型评价［J］.复杂油气藏，2014（2）：57-60.CHEN Liang,SUN Lei.Evaluating calculation methods of Z-factor for CO2gas reservoir［J］.Complex Hydrocarbon Reservoirs,2014（2）: 57-60.

［3］HALL K R,YARBOROUGH L.A new equation of state for Z-factor calculations ［J］.Oil and Gas Journal,1973,71（25）: 82-92.

［4］DRANCHUK P M,PURVIS R A,ROBINSON D B.Computer calculation of natural gas compressibility factors using the Standing and Katz correlation［C］.Annual Technical Meeting,Petroleum Society of Canada,1973.

［5］DRANCHUK P M,ABOU-KASSEM H.Calculation of Z factors for natural gases using equations of state ［J］.Journal of Canadian,Petroleum Technology,1975,14（3）:34-36.

［6］何更生，唐海.油层物理［M］.北京：石油工业出版社，2011.HE Gengsheng,TANG Hai.Petro physics ［M］.Beijing:Pet-roleum Industry Press,2011.

［7］WICHERT E,AZIZ K.Calculate Z's for sour gases ［J］.Hydrocarbon Processing,1972,51（5）: 119-124.

［8］李士伦，王鸣华，何江川.气田与凝析气田开发［M］.北京：石油工业出版社，2004.LI Shilun,WANG Minghua,HE Jiangchuan.The development of gas and condensate gas field［M］.Beijing: Petroleum Industry Press,2004.

（修改稿收到日期 2017-02-21）

〔编辑 薛改珍〕

Evaluation on the prediction method of Z-factor of gas condensate with water vapor in Yacheng Gasfield

XIONG Yu1,LI Peisi1,DENG Dan1,MO Jun1,LI Wei2,LI Yuelin3
1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu610500,Sichuan,China;
2.Xinglongtai Oil Production Plant,PetroChina Liaohe Oilfield Company,Panjin124000,Liaoning,China;
3.CNOOC Zhanjiang Production Department Branch,Zhanjiang524000,Guangdong,China

Z-factor of natural gas is one important parameter for gas reservoir engineering calculation,and it is mostly calculated by means of empirical formula.Different calculation methods are different in application range and precision,and the effect of water vapor is usually neglected in the conventional methods used for calculating Z-factor of gas condensate,so the calculation error of Z-factor is larger.In this paper,different calculation methods were adopted respectively to deal with these difficulties.Then,Z-factor of gas condensate with water vapor was calculated by using correction models (e.g.WA and Casey).Finally,the calculated Z-factor was compared with the measured value,and the applicability of three models (i.e.,HY,DBR and DAK) to calculate Z-factor of gas condensate with water vapor was evaluated.It is indicated that when Z-factor of gas condensate with water vapor is calculated,the error of Z-factor which is corrected by the correction model is much smaller.The precision of three methods (i.e.,HY,DBR and DAK) varies with the value ofreduced pressure (pr).Their calculation precision is similar while 0≤pr≤3.87.The calculation precision of HY and DAK is higher while 4.84≤pr≤6.56.And the calculation precision of DAK is much higher while 3.87≤pr≤4.84 and 6.56≤pr≤7.59.

gas condensate with water vapor; Z-factor; calculation method

熊钰，李佩斯，邓丹，莫军，李玮，李跃林.崖城气田含水汽凝析气偏差因子预测方法评价［J］.石油钻采工艺，2017，39（3）：271-274，281.

TE332

：A

1000–7393（2017 ）03–0271–04DOI:10.13639/j.odpt.2017.03.003

: XIONG Yu,LI Peisi,DENG Dan,MO Jun,LI Wei,LI Yuelin.Evaluation on the prediction method of Z-factor of gas condensate with water vapor in Yacheng Gasfield［J］.Oil Drilling & Production Technology,2017,39(3): 271-274,281.

国家自然科学基金重点项目“致密气藏储层干化、提高气体渗流能力的基础研究”（编号：51534006）。

熊钰（1968-），1995年毕业于西南石油大学油气田开发专业，现从事复杂气田开发、油气藏工程、注气提高采收率、流体相态等方面的教学与研究工作。通讯地址：（610500）四川省成都市新都区西南石油大学石油工程学院。E-mail：2792234735@qq.com

李佩斯（1992-），主要研究方向为气田开发理论与方法，在读硕士研究生。通讯地址：（610500）四川省成都市新都区西南石油大学石油工程学院。E-mail：351884155@qq.com