实验教学SCARA机械臂控制算法研究与实现

姚晓通 潘影丽 高 宇

(兰州交通大学电子与信息工程学院 甘肃 兰州 730070)

实验教学SCARA机械臂控制算法研究与实现

姚晓通 潘影丽 高 宇

(兰州交通大学电子与信息工程学院 甘肃 兰州 730070)

针对实验教学，设计一种开放式的SCARA教学机械臂，把对控制算法的研究作为教学重点。首次采用仿真设计和实物设计，作为示教的两个主要部分。通过D-H参数法确定运动学方程，根据运动学方程对机械臂进行了正逆运动学分析，结合轨迹规划完成机械臂运动规划。MATLAB建立机械臂模型，通过仿真模型运动验证了前期控制算法分析的准确性。利用Visual Studio 2013实现算法，完成上位机控制系统，通过上位机编程控制机械臂完成物体搬运工作。机械臂能够精准地实现旋转和搬运功能，并验证了控制算法研究和仿真设计的正确性，能够较好地达到实验教学的需求。

SCARA MATLAB 仿真 轨迹规划 运动控制

0 引 言

随着科学技术水平的不断提高，工业机器人(机械臂)已经大量地应用到生产生活中。机器人作为一个新兴的技术，涉及到了多个领域、各个学科。随着科技的发展，机器人技术也逐渐深入到教育领域。本文专门针对实验教学机器人，而设计制造SCARA机械臂，作为实验教学的研究模型。

MATLAB平台下的Robotic-Tools工具是研究机械臂中应用最广的仿真平台。文献[1]采用MATLAB介绍了机器人在实验教学中的应用，文献[2-3]采用了MATLAB和ADAMS联合仿真平台。文献[4]运用OpenGL环境创建机械臂模型，ADAM、OpenGL都具有很好的三维模型，使仿真结果更直观。本文通过MATLAB和实物机械臂联合，采用PC+控制卡方法，通过Visual Studio 2013完成上位机控制，以真实的机械臂演示，能更好、直观地验证实验结果的真实性。

1 机械臂的模型设计

SCARA机械臂，包括三个旋转关节和一个移动关节。SCARA机械臂定位精度高、运动速度快，适合于平面定位和垂直方向的装配作业。SCARA型机械臂的三维模型如图1所示。

图1 SCARA机械臂结构图

对图1的机械臂，建立连杆坐标系如图2所示。每个连杆都可以通过用于描述连杆本身和用于描述连杆之间的连接关系的运动学参数描述[5]，其分别为：单根连杆参数：ai(连杆长度)、αi(连杆扭脚)；相邻连杆之间的参数：di(连杆距离)、θi(连杆转角)。

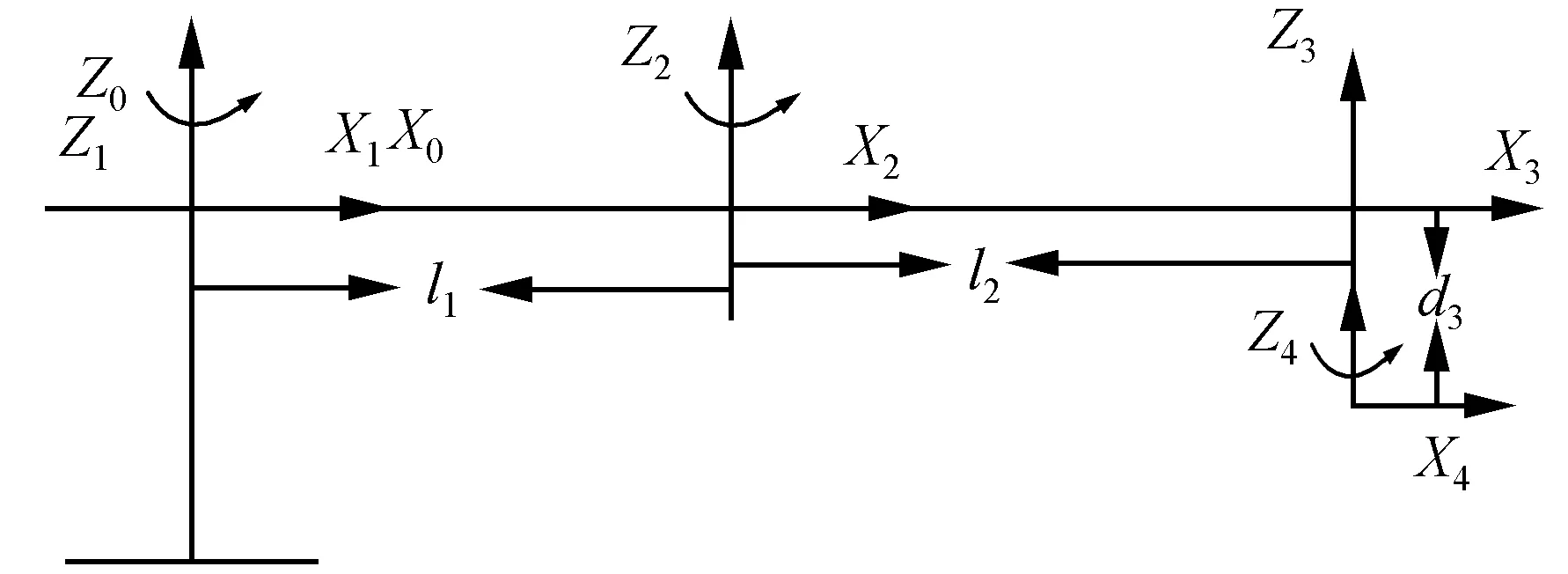
图2 D-H法建立的坐标系

根据图2坐标系可得出D-H参数，如表1所示。

表1 D-H参数表

2 机械臂的控制算法

实现机械臂控制算法的整个过程是根据D-H法建立的坐标系写出变换矩阵，根据变换矩阵写出每个坐标系相对于基坐标系的齐次变换矩阵；再根据每个坐标系的齐次矩阵求出正、逆解，同时根据一定的任务寻求一条连接起点到终点的最优或次优有效路径。

2.1 正运动学分析

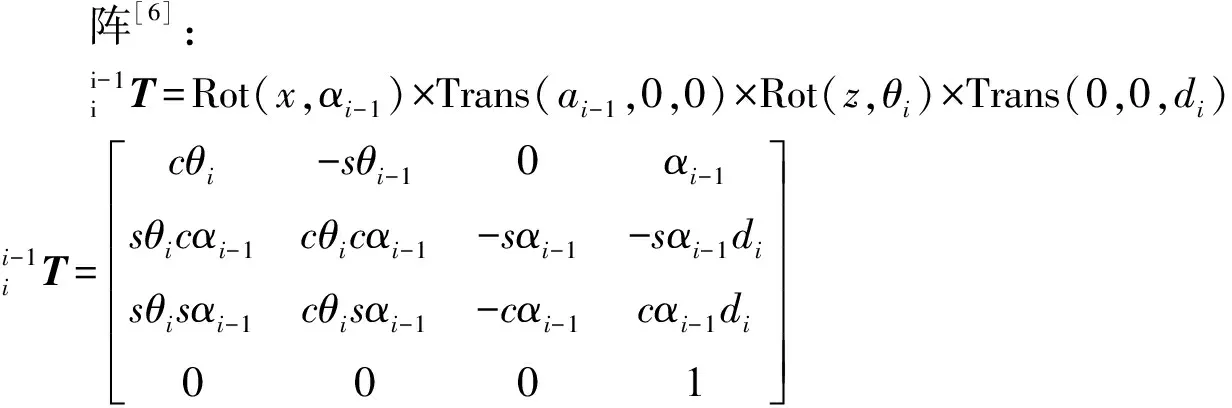
(1)

(2)

因此，对于本文SCARA教学机械臂，i=4时，确定末端执行器坐标系相当于基坐标系的变换矩阵为：

通过各连杆变换矩阵相乘，可以得到SCARA机械臂末端执行的位姿方程：

(4)

通过式(4)得到末端位置矩阵：[pxpypz]T,

(5)

(6)

(7)

(8)

2.2 逆运动学分析

逆运动学的求解是指机械臂的末端执行器的笛卡尔空间到各个关节空间的映射关系。逆解求解比正解复杂，需要考虑解的存在性、多重解等问题[7]。

(9)

对式(9)两边乘上0T1的逆矩阵，并根据矩阵两边对应元素相等求解各个关节变量。

1) 求关节变量θ1为了分离变量，方程的两边同时左乘0T1(θ1)，得：

0T1-1·0T4=1T22T33T4

(10)

即：

根据式(10)矩阵对应元素相等的：

L(1,4)=R(1,4)：px·cosθ1+py·sinθ1=cosθ2·l2+l1

(11)L(2,4)=R(2,4)：-px·sinθ1+py·cosθ1=sinθ2·l2

(12)

根据式(11)得：

2) 求关节变量θ2，根据式(12)得：

(13)

3) 求关节变量d3，根据左右两边第三行第四列对应元素相等得：

L(3,4)=R(3,4)：d3=-pz

(14)

4) 求关节变量θ4，根据矩阵左右两边对应元素相等得：

L(1,1)=R(1,1)：

nx.cosθ1+nysinθ1=cosθ2·cosθ4-sinθ2·sinθ4

(15)

L(2,1)=R(2,1)：nx·-sinθ1+ny·cosθ1=sinθ2·cosθ4-cosθ2·sinθ4

(16)

根据式(15)、式(16)得：

(17)

2.3 轨迹规划

轨迹是指每个自由度的位置、速度和加速度的时间历程[8]。轨迹规划就是规划出具有平滑性和连续型的轨迹，从而保证实际工作中的机械臂在运动过程保持平稳无冲击。本文以关节空间规划对机械臂轨迹进行仿真并通过真实机械臂进行验证。

θ(t)=a0+a1t+a2t2+a3t3

(18)

(19)

(20)

把四个约束条件代入式(18)-式(20)中可以得到含有四个未知量的四个方程：

θ0=a0

(21)

(22)

0=a1

(23)

(24)

解方程可以得到：

a0=θ0

(25)

a1=0

(26)

(27)

(28)

通过式(25)-式(28)可以求出从任何起始关节角位置到期望终止位置的三次多项式。

3 仿真设计

利用MATLAB平台的机器人工具箱——Robotics Toolbox[9]，采用改进D-H建模方法，改进的D-H建模方法可有效的弥补标准D-H建模与实物的偏差[10]。建立机械手运动学模型，代码如下：

L1=link([0 0 0 0 0],′modified′);

L2=link([0 95 0 0 0],′modified′);

L3=link([0 100 0 0 1],′modified′);

L4=link([0 0 0 -40 0],′modified′);

r = robot({L1 L2 L3 L4});

r.name = ′SCARA′;

drivebot(r);

仿真结果如图3所示。

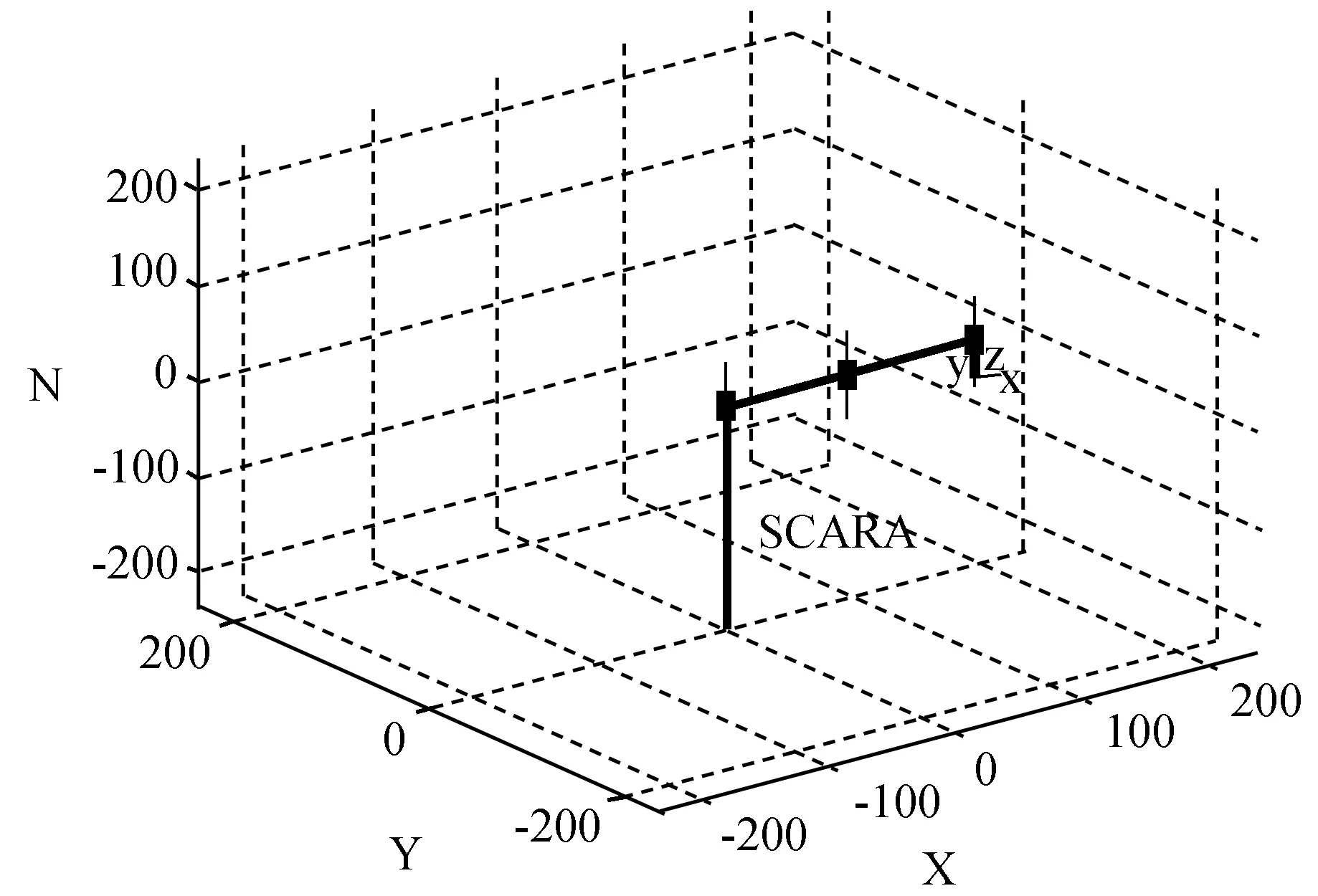
图3 SCARA机械臂模型图

根据上面轨迹规划计算，应用MATLAB仿真[11]，设置其由qa=[-0.000 062 0.000 178 0.000 000 -0.000 117]运动到qb=[-0.522 315 1.504 080 0.000 000 -0.981 765]。设置时间向量t=[0∶0.015∶1]，可以观察各个关节的运动情况如图4-图6所示。

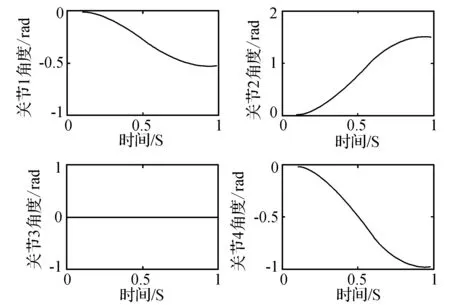
图4 关节角度与时间的关系

图5 关节速度与时间的关系

图6 关节加速度与时间的关系

通过以上仿真结果，观察每个关节的运动。通过观察机械臂从qa运动qb过程中各个关节角度、速度、加速度随时间的变化仿真结果，可以确定各连杆没有运动错位的情况，并且各个关节可以平稳地由起点运动到终点，从而确定规划可以满足运动要求。

4 机械臂实物设计

本文采用PC+控制卡方法，PC机完成运动规划任务，运动控制卡完成运动控制功能，其成本较低，适合研究讨论，验证理论结果。

4.1 SCARA机械臂控制系统的组成

SCARA四自由度机械臂控制系统由工业机械臂、控制箱、计算机组成。由于平面机械臂主要实现速度快、精度高等特性，因此采用基于FPGA实现的多路步进电机控制[12]。FPGA拥有丰富的内部资源和大量的IP核，具有速度快、精度高、指令并行执行、硬件扩展方便等优点。实物如图7、图8所示。

图7 机械臂实物图 图8 控制箱实物图

4.2 控制系统的软件设计

本文设计了基于PC机USB总线的运动控制器，该控制器可以同时控制多个步进电机。开发了一套基于Windows具有交互式界面及开放式结构的控制软件，该控制软件利用Visual Studio 2013并且通过动态链接库编写运动控制函数，可以直接对硬件接口进行访问，便于底层访问控制。四自由度机械臂控制界面分为参数设置模块、正运动学分析模块、逆运动学分析模块，运动控制模块、结果显示模块。

如图9所示上位机部分界面控制，包含对设备的打开，让设备处于开始工作状态；机械臂参数的设置，包含机械各个臂的长度。正运动学仿真，输入两点参数后，会把运动停止后的关节参数显示出来。逆运动学仿真，当在末端抓持器的位姿编辑框中输入位置时，关节角编辑框中会显示对应角度的变化。另外为了更好实现对机械臂运动控制设置了控制末端按钮，控制其对物体的“拿起”和“放下”，对突发事件发生设置“急停”。对机械臂的运动的次数设置，并可以随时控制其“暂停”“开始”。下半部分界面主要是实现运动结果显示，对机械臂运动的一下微调控制，可以设置机械臂的运动的方向，对每个轴分开控制。

图9 界面整体图

实验测试结果：运行后设备打开，调用相应函数设置机械臂参数和机械臂算法参数，在测试时，起始点和终止点的关节角速度、加速度都默认设为零。上位机界面给出机械臂运动轨迹，实物机械臂可以到达预设的位置点并完成搬运动作。结果如图10所示。

图10 运行结果图

算法实现如下：

1) 正解过程：

输入参数：r_theta_move关节坐标(θ1，θ2，d3，θ4)；

输出参数：p_clamp_point机械臂夹具坐标。

bool flag;

flag=bool robot_forward(Rotational_struct

r_theta_move,

HPosition *p_clamp_point_ptr)

If(flag==TRUE)

{计算出p_clamp_point坐标}

2) 反解过程

输入参数：HPosition p_clamp_point机械臂夹具末端坐标;

输出参数：float clamp_theta夹具姿态角度θ。

bool flag;

Rotational_struct left_theta_move;左臂关节坐标(θ1，θ2，d3，θ4)；

bool left_workspace; 左臂反解是否成功

Rotational_struct right_theta_move;左臂关节坐标(θ1，θ2，d3，θ4)；

bool right_workspace;左臂反解是否成功

flag=bool robot _inverse (p_clamp_point,

clamp_theta,

r_left_theta_move,

left_workspace,

r_right_theta_move,

right_workspace)

if(left_workspace==TRUE)

{解出r_left_theta_move左臂姿态时的关节角}

else

{由p_clamp_point、clamp_theta确定夹具姿态不在机械臂左臂工作空间}

if(right_workspace==TRUE)

{解出r_right_theta_move右臂姿态时的关节角}

else

{由p_clamp_point、clamp_theta确定夹具姿态不在机械臂右臂工作空间}

5 结 语

通过利用D-H参数法建立了SCARA机械臂的模型，对SCARA教学机械臂的整体设计规划与实现，能较好地完成预计的控制目标，完成动作和达到控制要求。通过不断地对机械臂的调试和与对硬件的修改，实现了灵活的控制平台。同时运用各种运行信息的实时传输，再与上位机的联合调试，能够很好地完成对各个关节的精确定位、各项功能都能较好地实现，并且可以支持遥控功能。此实验教学机械臂控制平台的设计与研究，能很好地满足教学实验需求，便于学生自主的安装和调试，不仅巩固了学生的理论知识，而且学生的创新意识和动手能力得到很好的培养和提高。

[1] 谢斌，蔡自兴.基于MATLAB Robotics Toolbox的机器人学仿真实验教学[J].计算机教育，2010(19):140-143.

[2] 马如奇，郝双辉，郑伟峰，等.基于MATLAB与ADAMS的机械臂联合仿真研究[J].机械设计与制造，2010(4):93-95.

[3] 高东强，杨磊，韩昆，等.SCARA机械手的轨迹规划及运动学分析[J].机械设计与制造，2015(1):269-272S.

[4] 宋西平，李国琴，罗陆锋.基于OpenGL的五自由度机械臂的运动学仿真[J].机械设计与制造工程，2015,44(12):18-21.

[5] Craig J J.机器人学导论[M].机械工业出版社,2006.

[6] 潘磊，钱炜，张志艳，等.四自由度机械臂运动学分析及Matlab仿真[J].机械科学与技术，2013,32(3):421-425.

[7] 郭发勇，梅涛，赵江梅.D-H法建立连杆坐标系存在的问题及改进[J].中国机械工程,2014,25(20):2710-2714.

[8] 刘磊.SCARA型四自由度机械臂轨迹规划算法的设计与实现[D].安徽：安徽工程大学,2013.

[9] Corke P I.A robotics toolbox for Matlab[J].IEEE Robotics and Automation Magazine,1996,3(1):24-32.

[10] 臧庆凯，春贵，闰向磊.MATLAB分析与轨迹规划仿真[J].工业控制计算机,2014,27(8):12-14.

[11] 张舒曼.基于Matlab的机器人运动学械臂控制系统研究[D].湖北：湖北工业大学,2014.

[12] 李远重.基于FPGA的5自由度工业机的PUMA560机器人运动仿真研究[J].广西科学院学报，2010,26(4)：397-400.

RESEARCH AND IMPLEMENTATION OF SCARA MANIPULATOR CONTROL ALGORITHM IN EXPERIMENTAL TEACHING

Yao Xiaotong Pan Yingli Gao Yu

(CollegeofElectronicalandInformationEngineering,LanzhouJiaotongUniversity,Lanzhou730070,Gansu,China)

Aiming at the experimental teaching, an open SCARA teaching manipulator is designed, and the research on the control algorithm is the teaching key points. Simulation design and physical design are used for the first time, as the teaching of two main parts. According to the D-H parameter method, the kinematics equation is determined. The kinematics equation is used to analyse the forward and inverse kinematics of the manipulator, and the motion planning of manipulator is completed according to the trajectory planning. The model of the manipulator is established by MATLAB, and the accuracy of the pre control algorithm is validated by simulation model movement. The algorithm completes PC control system by using Visual Studio 2013, finally through the PC programming control the manipulator to complete object handling work. The manipulator can accurately realize the rotation and handling function to verify the correctness of the control algorithm and simulation design, and can better meet the needs of experimental teaching.

SCARA MATLAB Simulation Trajectory planning Motion control

2016-09-08。甘肃省兰州市科技局资助项目(213188)。姚晓通，副教授，主研领域：计算机测控，智能识别应用开发，物联网应用开发。潘影丽，硕士生。高宇，硕士生。

TP39

A

10.3969/j.issn.1000-386x.2017.06.019