基于稀疏正则化的高维数据可视化分析技术
2017-07-10陈海辉周向东施伯乐
陈海辉 周向东 施伯乐
(复旦大学计算机科学技术学院 上海 200433)
基于稀疏正则化的高维数据可视化分析技术
陈海辉 周向东 施伯乐
(复旦大学计算机科学技术学院 上海 200433)
高维数据可视化分析是数据分析与可视化领域的研究热点,传统的降维方法得到的低维空间往往难以解释,不利于人们对高维数据的可视化分析与探索。提出一种新的可视化解释器(Explainer)方法,将L1稀疏正则化特征选取引入到高维数据的可视化处理过程中,建立起高层语义标签与少量的关键特征之间的联系。通过可视化设计与实验验证了该方法可以有效改善高维数据的可视化分析性能。
高维数据 特征选取 稀疏学习 可视化分析 降维 投影
0 引 言
高维数据可视化分析将高维数据处理与可视化呈现结合,如运用数据降维技术,结合视觉编码手段进行数据分析与探索。近年来高维数据可视化分析技术在实际应用中显示出越来越重要的价值。
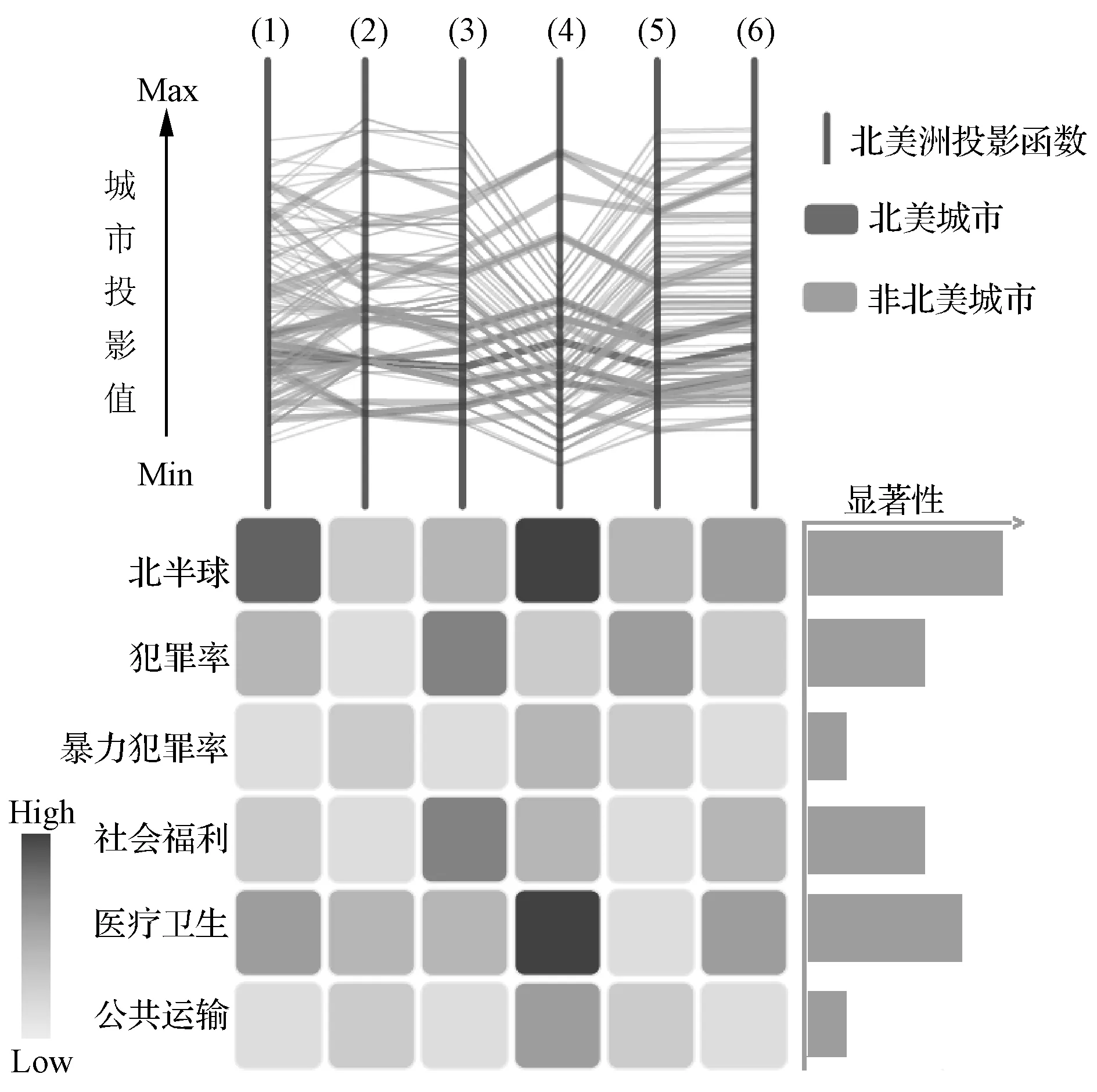
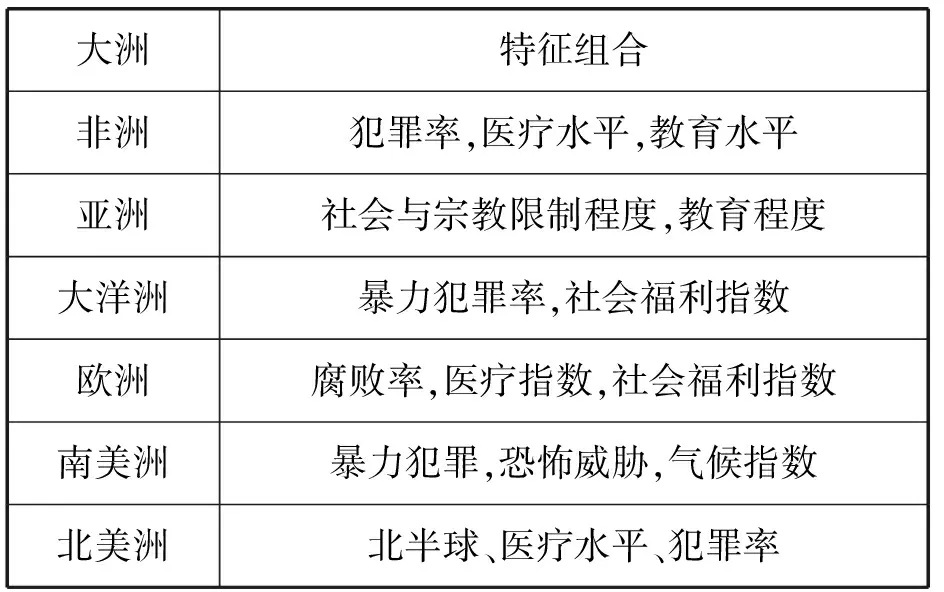
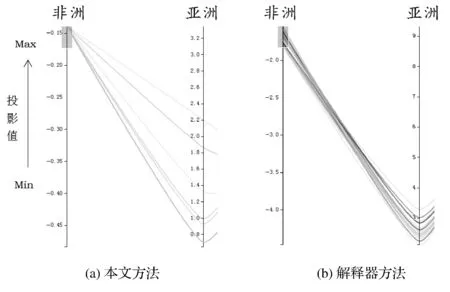
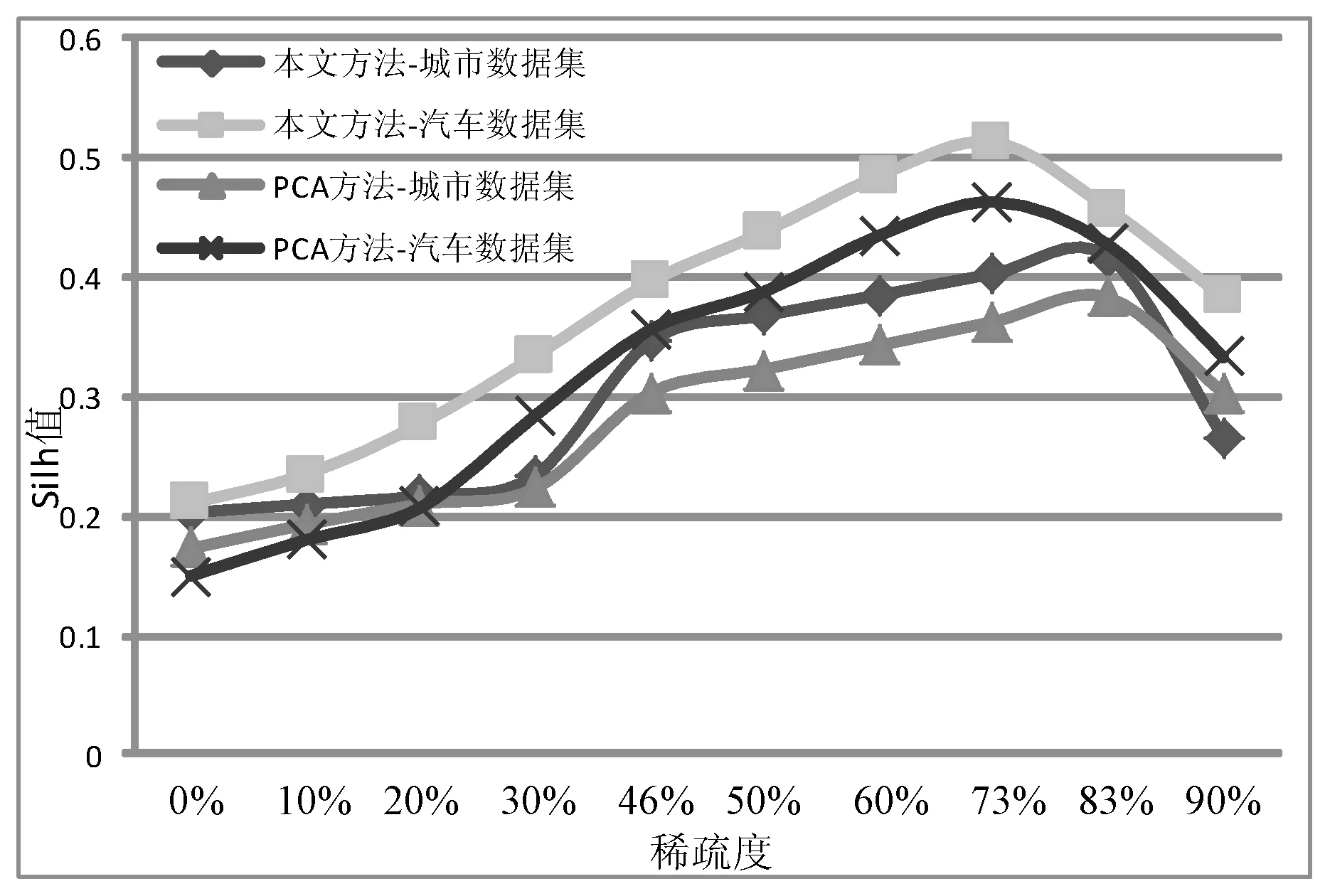
高维数据可视化分析中常用的数据降维方法,如主成分分析法[1]等将N维高维数据点投射到新生成的K维空间中(K< 本文在解释器技术的基础上,提出一种新的针对层次化高维数据可视化分析的方法。我们使用基于L1稀疏正则化的层次分类器进行模型训练,实现数据特征的自动选取(即降维处理)。通过参数调节模型的稀疏性,可以得到不同的特征组合,以及相应的解释器(投影函数),从而建立起多方位的从高维特征到低维特征、低维特征到高层语义之间的联系,克服了直接从高维特征到语义空间映射的可视化困难。在两个通用的可视化数据集上进行了可视化设计与实验,验证了本文提出的方法可以有效改进传统解释器投影技术的可视化分析性能。特别是在平行坐标图和散点图等常用的高维数据可视化技术中,本文提出的方法表现出更好的数据分离能力,改进了高维数据可视化分析的效果 高维数据可视化分析通常由数据降维算法和可视化编码方法组合而成。投影追踪算法[2]将高维数据投影到低维子空间上,并通过极小化投影指标函数,寻找出反映原高维数据的结构特征的投影,提高低维空间上数据可视化分析的性能。文献[3-4]对投影追踪算法进行改进,将投影指标函数应用到特征变量上,并运用交互式可视化方法从不同视角进行数据分析与探索。文献[5]将投影追踪技术应用到散点图矩阵可视化上,使得在单一空间内可以展示更多的散点图。上述工作将高维数据变换投影到低维空间的过程中,往往缺乏与用户知识的结合,基本上可以视为非监督学习类型的高维数据可视化技术。 近年来,将用户知识融入高维数据的可视化分析的研究越来越多,文献[6-7]中用户驱动式的降维算法如PPCA(Probabilistic PCA)、 GTM(Generative Topographic Mapping)根据用户定义的视角和条件,调节参数产生各种投影函数,方便用户进行问题驱动的数据探索与分析。文献[8]提出LAMP算法,通过引入正交投影理论,将用户知识引入到投影函数学习的过程中。LAMP算法有效地将两个不相关的高维数据集在同一可视化平面展示,用以探索不同来源数据之间的潜在联系。这些投影函数往往都是用来组织数据的分布,并不能解释特征与变量之间的联系。 文献[9]中通过为高维数据打上标签,并学习得到相应的投影函数,用以解释特征与变量之间的联系。文献[10]在高维数据处理过程中使用sugiyama算法减少折线稠密交叉情况,用以解决高维数据平行坐标图可视化时常见折线聚集的问题。文献[11]中提出的解释器技术采用监督学习方法对有关分类器进行学习,把获得的线性分类函数作为从特征空间到语义空间的投影工具(也称为解释器)。通过对待分析数据进行投影(或解释),实现数据的分析与理解。但是对高维数据的分析,仍然是从高维特征空间到语义空间的映射,无法克服高维数据本身引起的“维灾问题”。 2.1 解释器技术 解释器技术[11]利用用户知识来提高数据可视化分析的性能。即根据用户对数据进行语义标注,采用有监督学习技术,对线性分类器进行训练: f(x)=w·x+b (1) 式(1)中线性分类器f(x)被看作连接高层语义与底层特征之间的投影函数,称为解释器。 根据用户知识得到的解释器可以用来重新组织数据,并与可视化编码相结合实现数据的可视化分析和探索。在文献[11]的基础上,文献[12]引入解释器技术学习包含用户知识的投影函数,应用到气候模型的可视化分析领域。文献[13]把解释器作为交互式投影方法,随着用户视角改变,交互式探索高维数据在用户语义空间的分布特性。 但是,利用传统的解释器技术对高维数据的分析,仍然面临高维数引起的“维灾问题”,应用到平行坐标图,散点图等常见可视化方法中,不同类别数据之间遮挡情况严重,耦合与分离效果较差,影响可视化效果。因此,本文基于L1稀疏正则化分类技术,提出一种对高维层次数据可视化分析的新方法,即通过数据特征自动选取建立起低维特征空间与语义空间的联系,使高维数据可视化分析获得更好的效果。 2.2 基于L1正则化的层次分类器模型 图1 城市的层次类标签结构 层次化数据集是一种常见的数据分析对象,图1是关于世界各国城市数据集的语义标签层次结构[11,16]。层次数据集一般使用树结构进行描述:令A(i)和S(i)分别代表标签结构树上节点i的祖先节点和兄弟节点集合,并且令A+(i)=A(i)∪i。令X∈Rd为输入数据集的特征空间,维数是d。Y={1,2,…,m}为层次树上除了根节点0以的其他节点对应的标签编号。每一个层次标签对应唯一的编号。 本文采取的对高维层次数据可视化分析方法主要包括:基于L1正则化的层次分类器模型的训练;可视化分析设计两个部分。本节主要介绍层次分类技术;可视化设计在实验部分详细介绍。 (2) 式(2)中R(w)是正则化项,用以防止训练得到的模型过拟合。{ξk},∀k∈{1,2,…,N}是损失因子中的松弛变量。参数C1用以控制正则化项和损失项的平衡。 (3) 式(3)中R(w)采用混合的正则化方法[15],第一项使用L1稀疏化方法对模型的参数进行约束,这样既能增加层次分类的判别区分能力,又能够同时学习出一组稀疏的真正有贡献的特征组合。在后续的层次数据可视化分析和探索中,帮助学习语义标签与对应特征组合之间的关联。C2可以用来控制稀疏化的程度。第二项和第三项是层次分类的正交正则化约束,使得不同层次和兄弟节点分类器使用各自特有的特征组合,提高分类性能。关于模型的参数估计,本文采用文献[14-15]给出的正则对偶式平均RDA(Regularized Dual Averaging)方法。 3.1 可视化分析案例 本文以城市数据集[16]和UCI汽车数据集[17]为案例进行可视化探索的实验与对比分析。城市数据集包含4层数据:城市、国家、地区和大洲,数据维度45维。汽车数据集包含2层数据:汽车类型和汽车品牌,数据维度26维。 可视化实验分为两部分: 1) 本文设计的解释器-特征选择图帮助可视化探索数据语义标签与显著特征的关系。 2) 常见高维数据分析的可视化效果对比:在平行坐标图和散点图对比使用本文方法和解释器方法的可视化效果。 3.2 解释器-特征选择图 本文设计了如图2所示的解释器-特征选择图。该图形展示了不同的北美洲投影函数与相应的特征组合之间的关系。通过调节L1惩罚项参数,可以得到6组北美洲投影函数和与之对应的特征组合。用平行坐标图中的不同垂直轴线,代表了不同的北美洲投影函数。北美洲的城市(图中深色折线)与非北美洲城市(图中浅色折线)分别用6个投影函数在平行坐标图上作投影映射。 图2 解释器-特征选择图 图2以热力图的形式展示投影函数与其对应的显著特征。每一列方格代表不同的特征组合,与上方的轴线(即投影函数)对应。每一行代表一种特征。热力图中方格颜色深浅代表该特征的显著性。热力图右边用直方图统计每一种特征的平均显著性。 图2中每条轴线上深色折线基本都在浅色折线的上方。在北美洲投影函数下,北美洲的城市对比于非北美轴的城市,往往具有更高的投影值,证明了本文将L1稀疏化方法引入分类器学习的有效性。 通过解释器-特征选择图,发现北美洲城市中最显著的特征,主要是医疗卫生水平、犯罪率等。这样就可以发现高层语义标签与特征之间的潜在关系,用户可以重点观察这些特征进一步分析数据。 表1为将本文方法应到城市数据集,根据解释器-特征选择图分析得出的各个大洲的最具有显著性的特征组合。根据表1中得到的所有8个特征,绘制出图3所示城市数据集的平行坐标图。可以发现,非洲城市(深线)和亚洲城市(浅色)在各个特征上的表现的模式具有显著的区分度和离散度,可以非常方便地对不同城市(折线)进行观测与分析。原始45维的数据集在这8个维度就可以得到很显著的区分性,证明了解释器-特征选择图可以方便高维数据的可视化分析。 表1 大洲的特征组合 表2为将本文方法应到汽车数据集,根据解释器-特征选择图分析得出的各个汽车类型的最具有显著性的特征组合。 图3 城市数据集的平行坐标图 表2 汽车类型的特征组合 3.3 改进的解释器投影效果 本节对比本文方法与解释器方法投影效果,分别应用L1稀疏正则化方法和解释器方法得到“非洲”语义标签对应的投影函数。经过投影变换,将城市数据投影到非洲轴上。 图4 本文方法与解释器方法投影效果对比 如图4所示,在非洲解释器上投影值排名前10%的城市的分布,可以发现本文方法中非洲城市主要分布在非洲轴的上部分,不是非洲的城市主要分布在轴下方,而解释器方法中非洲城市分布在非洲轴的中上部分,明显本文方法投影效果比解释器方法更好,对于提高投影的准确性具有显著作用。 3.4 改进的平行坐标图效果 如图5所示,同样以非洲与亚洲两个轴线为例,分别应用本文方法和解释器方法作平行坐标图。通过对数据作筛选,取在非洲轴投影值最高的10%的数据。可以发现右图中,数据折线很明显聚集在一起(b),并不利于发现这一系列数据在其他轴线上的分布特性。而我们使用稀疏化方法(a)中,数据折线相对离散,分离效果明显,便于对数据单独分析和可视化展示。引入L1稀疏化特征选择方法,表现出了更好的数据分离能力,对于平行坐标图的数据线条聚集问题有明显改进。 图5 平行坐标图折线分散效果对比 3.5 改进的散点图效果 由于散点图平面较小,当数据数量很高时,数据点聚集现象就会变得很严重,极大影响可视化图形的阅读性。因此,可视化数据点之间的聚集与离散性指标Silhouette (Silh)系数[18]通常用来评价散点图可视化效果。式(4)中,ax代表点x与同类别的其它点之间距离的平均值,bx代表点x与所有其它类别的点的距离的最小值。Silh的值的范围在-1到 1之间,Silh值越大代表更好的内聚性和分离性。 (4) 图6展示的是学习得到的关于非洲城市和亚洲城市投影函数后得到散点图。图6(a)是解释器方法得到的散点图, Silh值为0.203。图6(b)是应用本文方法后得到低维空间的数据后,再使用PCA方法得到的散点图,Silh值为0.287。 图6(c)和图6(d)所示为本文方法在稀疏度为0.73、0.83时,Silh值分别为0.403和0.417均高于传统方法和PCA方法。说明本文方法在数据的散点图可视化时,耦合性和分离性效果表现更好。图7展示中将本文方法应用到汽车数据集合中,对比传统的解释器方法以及PCA方法,本文方法图7(c),图7(d)的Silh分别为0.485和0.513,获得了更好的结果。 图8为本文方法和传统的PCA方法应用到城市数据集和汽车数据集上的稀疏度-silh值图。可以发现随着稀疏度的提高,散点图的Silh值明显提高。但特征过于稀疏后,Silh也会明显下降。对比这两个数据集上的结果,发现本文方法相比于PCA方法,获得的Silh值都更大,可视化效果更好。 因此,本文方法相比解释器方法和PCA方法,对于多类别的数据在二维散点图展示时,明显提升数据的内聚性和分离性,不同类别数据点聚集情况明显减轻,方便了分析人员可视化探索数据。 通过可视化实验中对比效果,可以发现本文提出的基于高维层次数据可视化分析的方法,通过引入L1稀疏化学习的过程,不仅便于分析人员可视化探索高维数据语义标签与特征之间的潜在关系。通过可视化实验,本文方法对比于解释器方法和传统的PCA方法,在平行坐标图和散点图上的可视化效果更好,明显改进了图形中数据的聚集现象,提高数据分离效果,方便分析人员对高维数据的可视化探索。 图6 城市数据集-散点图效果对比 图7 汽车数据集-散点图效果对比 图8 稀疏度-silh值图 本文提出一种针对层次化高维数据进行可视化分析和探索的新方法。对层次结构数据集采用L1稀疏化分类器进行模型训练,实现语义标签与之紧密相关的数据特征的自动选取。通过参数调节模型的稀疏性,可以得到不同的特征组合,以及相应的高维数据解释器(投影函数),从而建立起了从高维到低维特征与高层语义之间的联系。通过可视化实验,证明了本文提出的方法可以改进解释器投影技术的可视化分析效果,特别是在平行坐标和散点图等常用的高维数据可视化技术中,本文提出的方法表现出更好的数据分离能力,可以有效改进高维数据的可视化分析效果。 [1] Jolliffe I T.Principal Component Analysis[J].Springer Berlin, 2010,87(100):41-64. [2] Friedman J H, Tukey J W. A Projection Pursuit Algorithm for Exploratory Data Analysis[J].Computers IEEE Transactions on, 1974, C-23(9):881-890. [3] Faith J. Targeted Projection Pursuit for Interactive Exploration of High-Dimensional Data Sets[C]//Information Visualization, 2007. IV’07. 11th International Conference. IEEE, 2007:286-292. [4] Seo J, Shneiderman B. A Rank-by-Feature Framework for Interactive Exploration of Multidimensional Data[J].Information Visualization, 2005, 4(2):96-113. [5] Wilkinson L, Anand A, Grossman R. Graph-theoretic scagnostics[C]//Information Visualization, 2005. INFOVIS 2005. IEEE Symposium on,2005:157-164. [6] Wang S P, Cao H F, Wei Ping W U. Observation-level interaction with statistical models for visual analytics[C]//Visual Analytics Science and Technology. IEEE, 2011:121-130. [7] Tejada E, Minghim R, Nonato L G. On improved projection techniques to support visual exploration of multidimensional data sets[J].Information Visualization,2003,2(4):218-231. [8] Paulo J, Paulovich F V, Danilo C, et al. Local Affine Multidimensional Projection[J].IEEE Transactions on Visualization & Computer Graphics,2011,17(12):2563-2571. [9] Kandogan E. Just-in-time annotation of clusters, outliers, and trends in point-based data visualizations[C]//Visual Analytics Science and Technology,2012:73-82. [10] Lu L F, Huang M L, Chen Y W, et al.Clutter Reduction in Multi-dimensional Visualization of Incomplete Data Using Sugiyama Algorithm[C]//International Conference on Information Visualization. IEEE Computer Society, 2012:93-99. [11] Michael G.Explainers: expert explorations with crafted projections[J].IEEE Transactions on Visualization & Computer Graphics, 2013,19(12):2042-2051. [12] Jorge P, Aritra D, Yaxing W, et al. Visual Reconciliation of Alternative Similarity Spaces in Climate Modeling[J].IEEE Transactions on Visualization & Computer Graphics, 2014,20(12):1923-1932. [13] Sedlmair M, Heinzl C, Bruckner S, et al. Visual Parameter Space Analysis: A Conceptual Framework[J].IEEE Transactions on Visualization & Computer Graphics, 2014,20(12):2161-2170. [14] Zhou D, Xiao L, Wu M.Hierarchical Classification via Orthogonal Transfer[C]//International Conference on Machine Learning,2011:801-808. [15] 产文. Web社区问答检索的关键技术研究[D].复旦大学,2014. [16] Buzzdata. Best City Contest[Z]. 2012. [17] Bache K, Lichman M. UCI Machine Learning Repository[Z/OL]. Irvine, CA: University of California, School of Information and Computer Science.2013. http://archive.ics.uci.edu/ml. [18] Tan P N, Steinbach M, Kumar V. Introduction to Data Mining, (First Edition)[M].Addison-Wesley Longman Publishing Co. Inc,2005. HIGH-DIMENSIONAL DATA VISUALIZATION ANALYSIS TECHNOLOGY BASED ON SPARSE REGULARIZATION Chen Haihui Zhou Xiangdong Shi Bole (SchoolofComputerScienceandTechnology,FudanUniversity,Shanghai200433,China) High-dimensional data visualization analysis is the research hotspot in the field of data analysis and visualization, the traditional low-dimensional dimension reduction method is often difficult to explain, and is not conducive to the visualization of high-dimensional data analysis and exploration. In this paper, a new visual explorer (Explainer) method is proposed to introduce the L1 sparse regularization feature selection into the high-dimensional data visualization process, and establish the relationship between high-level semantic tags and a few key features.The feasibility of the method is verified by visual design and experiment. It can improve the visualization performance of high dimensional data effectively. high-dimension data Feature selection Sparse learning Visualization analysis Dimension reduction Projection 2016-05-03。国家自然科学基金项目(61370157);上海市科技项目(14511107403);国网科技项目(5209401600 0A)。陈海辉,硕士生,主研领域:数据可视化。周向东,教授。施伯乐,教授。 TP3 A 10.3969/j.issn.1000-386x.2017.06.0051 相关工作
2 模 型



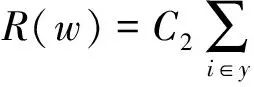
3 可视化实验





4 结 语
