加权整体最小二乘在GPS高程拟合中的应用

张鹏杰，郑晓晨，孟祥用，张珍肖

(石家庄市勘察测绘设计研究院，河北 石家庄 050019)

加权整体最小二乘在GPS高程拟合中的应用

张鹏杰*，郑晓晨，孟祥用，张珍肖

(石家庄市勘察测绘设计研究院，河北 石家庄 050019)

对于L=BX的工程问题，因为系数矩阵B和观测向量L的元素都是实测数据，并且有时候是不等精度获得的，存在或大或小的误差，因此在这些地方运用加权整体最小二乘求解是更加适用的。本文给出了加权整体最小二乘的解法，最后结合实例进行计算，得出利用加权整体最小二乘方法所得到的检核数据的残差最小的结论，验证了该理论的可行性，可以在工程应用中进行推广。

加权整体最小二乘；GPS高程拟合；随机模型；参数估计

1 引 言

GPS高程拟合在实际工程中应用很多，如何准确地把大地高H转化为正常高h，一些学者做出了研究，在文献[1]和文献[2]中作者对高程分区拟合进行了应用研究，在文献[3]中，针对高程拟合时多项式容易出现病态的问题，作者给出了解决办法。通过上述文献的案例数据，均表明采用多项式对GPS高程进行拟合的方法是可行的，但考虑到水准测量和GPS大地高测量均带有不同程度的误差，因此引进加权整体最小二乘的方法是更为适用的。

在文献[5]、文献[6]和文献[8]中，作者对整体最小二乘的方法进行了阐述，证明了在观测方程两边均含有误差的情况下，采用整体最小二乘方法对参数的估计更为准确。在文献[4]和文献[9]中，作者在整体最小二乘方法的基础上加入了权值，在参数估计的结果上显现了更大的优势。

2 加权整体最小二乘(WTLS)原理

对于观测方程：

(1)

可以列出误差方程：

(2)

加权整体最小二乘估计准则为：

VTPLV+vec(EB)TPBvec(EB)=min

(3)

以式(2)为条件，按Lagrange乘数法求解，构成目标函数为：

(4)

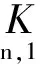
(5)

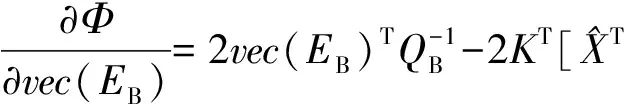
(6)

(7)

上式也可写成：

2KTEB+2KTB=0

(8)

由式(5)、式(6)分别得：

V=QLK

(9)

(10)

将上面两个式子代入误差方程式(2)得：

(11)

式中：

(12)

将式(11)代入式(8)，整理得：

(13)

上式即为未知参数的加权整体最小二乘解，我们采用迭代法来进行求解。求解步骤为：

(3)将K代入式(10)，求得vec(EB)，还原成EB；

当系数矩阵结构比较复杂时，单独对系数矩阵给予权值，QB的维数将会很大，这样会对将来的计算造成困难，此时我们可以对系数矩阵按列和行来给予权值。QL为观测值L的协因数阵，Q0为系数阵B的列向量协因数阵，Qx为系数阵B的行向量协因数阵，且有QB=Q0⊗QX。

3 GPS高程拟合

用于GPS高程拟合的数学模型很多，我们用最常用的是曲面拟合法。当GPS点布设成一定区域面时，可以采用曲面拟合法进行拟合，原理是：根据测区中公共点的平面坐标x、y和高程异常值ξ，用数值拟合法，拟合出测区的似大地水准面，再内插出待求点的高程异常值，从而求出待定点的正常高。

多项式曲面拟合法在拟合似大地水准面上较为准确，尤其是二次多项式曲面数学模型最为常用。即对于公共点上的高程异常值与平面坐标之间假定存在如下数学模型：

(14)

式中，a0、a1、a2、a3、a4、a5为模型待定参数。因此，区域内至少需有6个公共点。当公共点多于6个时，可组成误差方程：

V=BX-L

(15)

式中：

按最小二乘原理解求出模型待定参数a0、a1、a2、a3、a4、a5的数值。该拟合方法适合于平原与丘陵地区，实践表明，在一定范围内拟合精度可优于 3 cm。二次曲面拟合还可进一步扩展为多项式曲面拟合法，这时数学模型为：

写成矩阵形式，列误差方程表示与式(15)相同。

在实际应用中，如果把测区的似大地水准面假定为平面拟合模型，一般取式的前三项，对于测区面积不是很大，特别是测区内高程异常的变化有规律且地形变化平缓，已知点分布均匀的情况下，把测区的似大地水准面看成是一个二次曲面，则更为符合对似大地水准面的描述，根据过去的计算经验，能够达到比较理想的精度，所以在本文中我们采用二次曲面拟合法。

4 加权整体最小二乘在GPS高程拟合中的应用

为研究加权整体最小二乘(WTLS)的可行性和有效性，我们使用黄河某公路大桥数据来进行分析。该大桥处在黄河流经的平原上，桥址所处地区地势平坦，海拔在 1 200 m左右，桥址两端相对高差不到两米，两岸河床宽度在 1 000 m左右，交通便利，测区范围内的国家三角点和大地水准点资料都已收集齐全。点位分布如图1所示：

图1 某黄河大桥测区控制点分布图

测区内GPS点的高程异常值和平面坐标的数据列于表1。

原始数据 表1

表中，x、y为GPS点的平面坐标，ξ为经水准联测得到的该点处高程异常值。

现在我们取GPS点1、2、3、4、5、6、7、11、13、14、15、16、17、20、21来进行建立模型计算参数，GPS点8、9、10、12、18、19六个点来做外部检核。采用二次多项式曲面拟合方法进行拟合，公式为：

在WTLS的算法中，对系数矩阵B的权值按行和列来分别给予。列方程L=BX，其中：

PL为观测值权阵，Q0为系数阵列向量协因数阵，Qx为系数阵行向量协因数阵，In为n阶单位阵。

用最小二乘(LS)、一般整体最小二乘(TLS)和加权整体最小二乘(WTLS)三种方法分别对参数进行求取，并对外部检核数据进行计算，列于表2，然后计算其与测量值的残差，并绘图表示于图2。

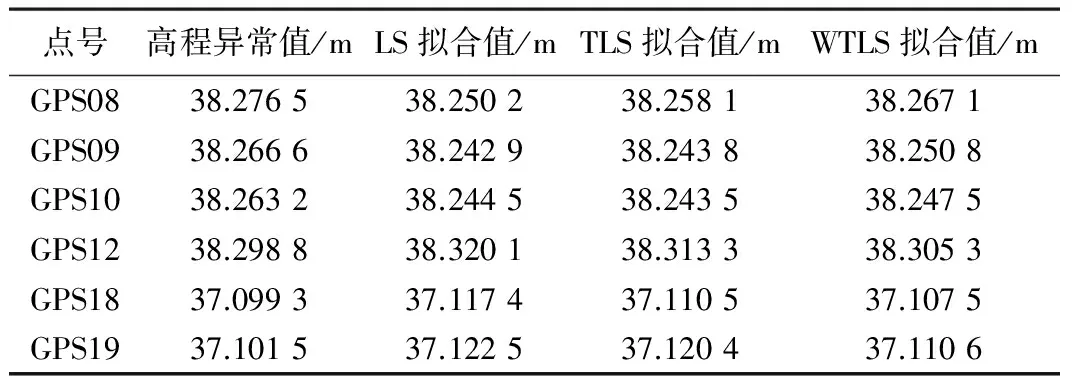
外符合数据 表2

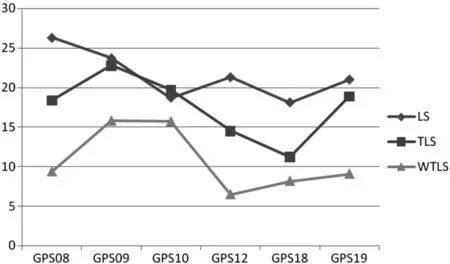
图2 检核点残差(单位/mm)

根据实际工程项目获得的数据，利用GPS高程拟合原理和方法，采用二次拟合模型来进行拟合，并用最小二乘、整体最小二乘和加权整体最小二乘来进行解算参数，求得高程异常值，将GPS测量得到的大地高转化为工程项目中需要的正常高，对结果进行比较分析。最后得出结论：从图2中可以很直观地看出，对于6个外部检核数据，加权整体最小二乘所计算的结果得到的残差均是最小的。通过与规范中水准等级限差进行比较，加权整体最小二乘可以达到三等水准精度要求，一般整体最下二乘可以达到四等水准精度要求，而最小二乘刚好也可以达到四等水准精度要求。这就说明加权整体最小二乘可以大大提高似大地水准面的拟合精度，为GPS高程数据的实际应用提供了有力的保证。

5 结 论

由于整体最小二乘方法建立的模型对方程的两边都进行了最小化约束，因此它比假设系数矩阵无误差的最小二乘方法更加合理，而加权整体最小二乘则是在整体最小二乘的基础上考虑了权值的问题，把对方程影响程度大的因子赋予了较大的权值，因此它又比一般整体最小二乘方法更加合理。计算结果说明了加权整体最小二乘法在高程拟合中的优势，该方法具有较好的理论研究价值和实用价值，应将这种方法广泛地应用于工程实际中来。

[1] 张鹏杰，赵新跃，廖习羽. 石家庄市GPS高程分区拟合的应用与研究[J]. 测绘地理信息，2013，38(5)：16～18.

[2] 高伟，卢秀山. GPS高程区域似大地水准面的分区拟合与平滑链接[J]. 测绘通报，2000，46(7)：11～16.

[3] 张恒璟，程鹏飞，孙小荣. 多项式拟合模型病态性问题的分析与应用研究[J]. 测绘通报，2012，7(4)：35～38.

[4] 张鹏杰，邱卫宁，程进伟等. 加权整体最小二乘求解线性模型参数及精度估计[J]. 测绘地理信息，2012，37(1)：4～5.[5] 邱卫宁，齐松玉，田丰瑞. 整体最小二乘求解线性模型的改进算法[J]. 武汉大学学报·信息科学版，2010，35(6)：708～710.

[6] De Moor B，Structured total least squares and L2 approximation problems.In：Van Dooren，et al eds.Linear Algebra and its Applications，Special Issue on Numerical Linear Algebra Methods in Control，Signal and Systems，1993，163～207.

[7] Pearson K. On lines and planes of closest fit to points in space. Phil Mag，1901，559～572.

[8] Van Huffel S，Vandewalle J. Analysis and properties of the generalized total least squares problem Ax=b when some or all columns in A are subject to error，SIAM J Matrix Anal Appl，1989，10：294～315.

[9] Burkhard Schaffrin. On weighted total least-squares adjustment for linear regression，Journal of Geodesy，2008，7.

[10] 陈为民，张旭东，符华年等. GPS高程测量代替等级水准测量的应用研究[J]. 武汉大学学报·信息科学版，2013，38(7)：828～831.

Weighted Total Least Squares Theory with Applications in GPS Elevation Fitting

Zhang Pengjie ，Zheng Xiaochen ，Meng Xiangyong ，Zhang Zhenxiao

(Investigation and Surveying Institute of Shijiazhuang City，Shijiazhuang 050019，China)

For the engineering problems of L=BX，the elements of coefficient matrix B and the observation vector L were measured data，and sometimes they were unequal precision obtained，exsisting error or big or small，so in these areas using the weighted total least squares solution was more suitable . This paper gave a method of weighted total least squares，finally calculated with examples，came to conclusion that the residuals of checking data by using the weighted total least squares method was least ，verified the feasibility of theory，could be applied in engineering application.

weighted total least squares；GPS elevation fitting；stochastic model；parameter estimation

1672-8262(2017)03-86-04

P228

B

2016—10—22

张鹏杰(1986—)，男，工程师，硕士，主要从事城市测量技术工作。