一种评估环形电感绕组损耗的方法
2017-07-07,
,
(福州大学电气工程与自动化学院,福建 福州 350108)
1 引言
在开关电源中,磁性元件扮演者重要的角色。磁性元件的损耗是影响效率的重要因素。随着开关频率提高,由于绕组的集肤效应和临近效应越显严重,评估绕组损耗也越显得重要。目前评估绕组损耗主要有两种方法:一是采用有限元软件仿真,二是采用数学模型理论分析。两者各有利弊:有限元仿真可以计算复杂模型,精度高,但是需要大量的计算机资源和时间为代价,而且,不适合优化设计;数学模型计算方便,易于绕组优化,但只能解决相对简单的结构,而且精度较低。
从上世纪60年代起,国外就有学者致力于绕组损耗的理论计算。著名学者P.L.Dowell提出的绕组一维等效模型至今仍被广泛采用。Dowell模型是把绕组等效成铜箔计算,其等效原则是:①磁力线必须平行于等效铜箔的长边;②等效前后保持直流电阻不变。针对平面PCB绕组和E-E或E-I等磁芯结构的绕组损耗已有不少的研究成果,然而环形磁性元件的研究甚少。
基于此,本文从Dowell模型入手,分析环形电感的绕组损耗。
2 Dowell模型的表达形式
2.1 直角坐标系下的Dowell模型
针对PCB绕组,传统的变压器绕组等结构,均可以将绕组等效成铜箔,采用直角坐标系建立模型,如图1所示。
在图1中,铜箔绕组的宽度为D,高度和深度为单位长度(1m),磁力线平行与铜箔导体的长边,磁场强度的幅值分别为H1和H2。
根据电磁场理论可知到体内的电磁场分布满足式方程组(1):
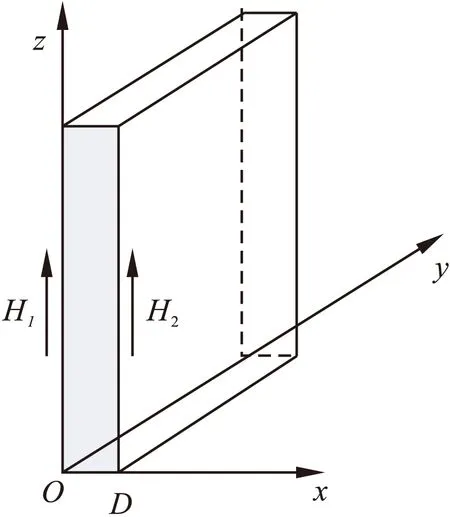
图1 一维铜箔绕组模型
(1)
电流密度和电场强度满足媒介方程:
J=γE
(2)
在正弦激励下,可以从(1)和(2)中推导出导体内部的磁场分布函数:
▽2H-jωμγH=0
(3)
在给定边界条件:
(4)
可以得到导体内部的电流密度分布如式(5)所示:
(5)
其中λ=jωμγ,相应的绕组损耗可以表示为:
(6)
2.2 柱坐标系下的Dowell模型

图2 环形绕组模型
对于有的结构,例如环形电感的内外层绕组,更适合等效成圆环,如图2所示。在图2中等效导体的内半径为Ri,外半径为Ro。磁场方向为θ方向,内外半径处的幅值分别为H1和H2。导体内部的磁场强度分布仍然满足方程(3)。
方程(3)在柱坐标系下展开是一个变系数的二阶微分方程:
(7)
方程(7)经过变形后可以改写为一个修正的Bessel方程:
(8)
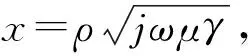
(9)
可以得到导体内部的电流密度分布如式(10)所示。
(10)
式(10)中λ=jωμr,I0,K0分别表示零阶第一类修正的Bessel函数和零阶第二类修正的Bessel函数,I1,K1分别表示一阶第一类修正的Bessel函数和零阶第二类修正的Bessel函数。相应的绕组损坏可以表示为:
(11)
3 环形电感的绕组损耗计算
环形电感的绕组损耗可以分为两个部分计算,分别是磁环内外层绕组和上下层绕组。
3.1 内外层绕组损耗计算
以环形电感的内层绕组为例。假设磁环内半径为R1,外半径为R2,导线的线径是d,导线和磁环表面的距离是δ。以磁环圆心为坐标原点,建立柱坐标系,将绕组等效成圆环状。绕组等效过程如图3所示。

图3 柱坐标系下Dowell模型绕组等效
根据直流电阻不变的原则,先把各个圆形截面的导体变成等面积的扇环。然后把各个扇环连接成一个圆环,填充整个区域。为保证绕组等效前后直流电阻不变,相应的电导率应修正为:
(12)
式(12)中N表示电感绕组的匝数;γ0表示导体的电导率。
取线径d为0.9mm,δ为0.2mm,对比R1为5mm的仿真值和柱坐标系下Dowell模型计算结果如图4所示。在频率20~500kHz范围内,误差均在10%以内。
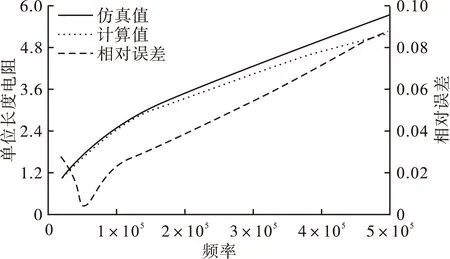
图4 R1为5mm的内层绕组单位长度电阻
针对外层的绕组,采用与内层绕组相同的等效方法。取线径d为0.9mm,δ为0.2mm,对比磁环外半径R2为8.33mm的仿真值和柱坐标系下Dowell模型计算结果如图5所示。
同样的线规和频率范围内,当磁环的外径R2增加到16.67mm。计算的单位长度电阻如图6所示。
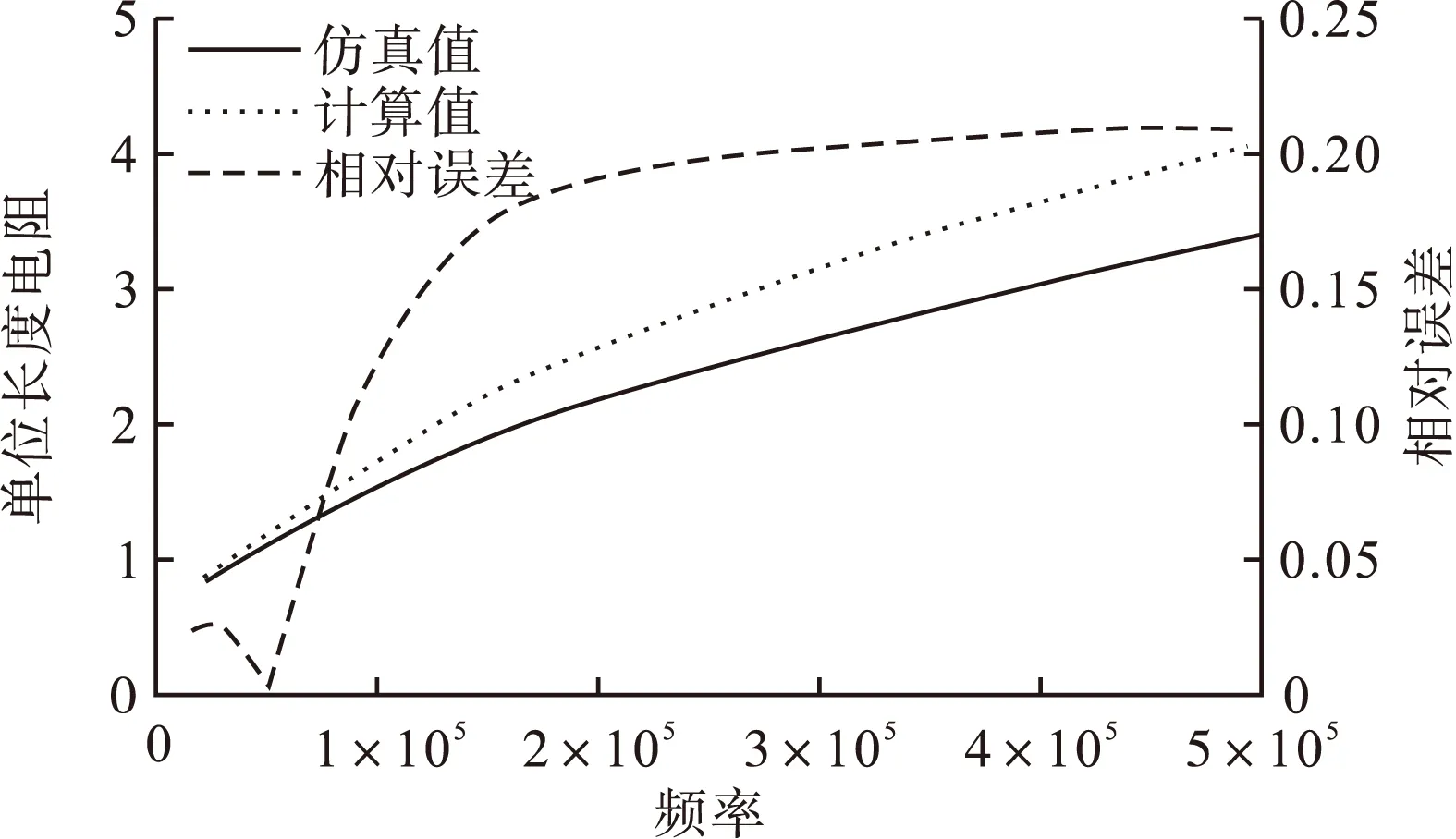
图5 R2为8.33mm的外层绕组单位长度电阻

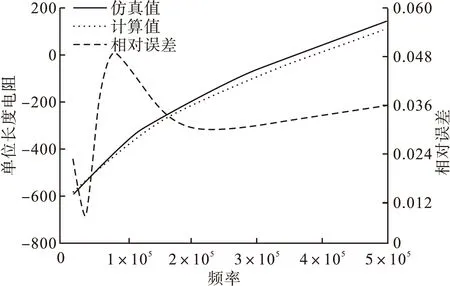
图6 R2为16.67mm的外层绕组单位长度电阻
从图5和图6可以看出,在磁环外径较小的时候,外层绕组之间的间距较大,磁场具有二维特征,除了θ方向的磁场外,ρ方向的磁场同样不可忽略。因此,计算的误差大。当磁环外径较大的时候,外层绕组排列紧密,磁场基本上只有θ方向,满足Dowell模型的等效原则。因此,误差可以降低。
3.2 上下层的绕组损耗计算
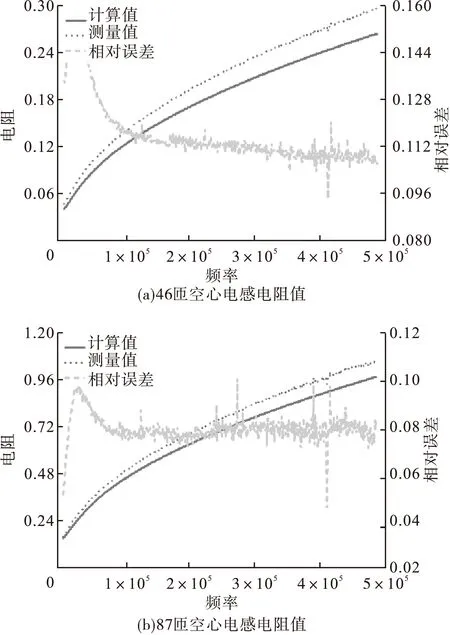
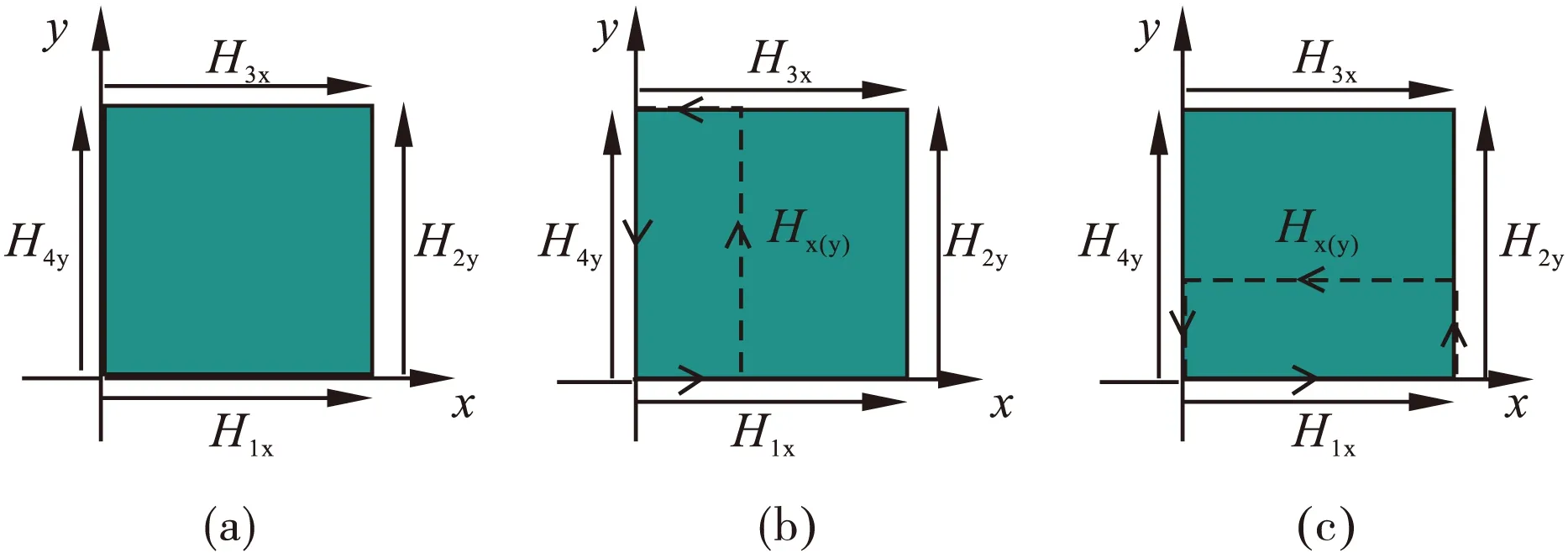
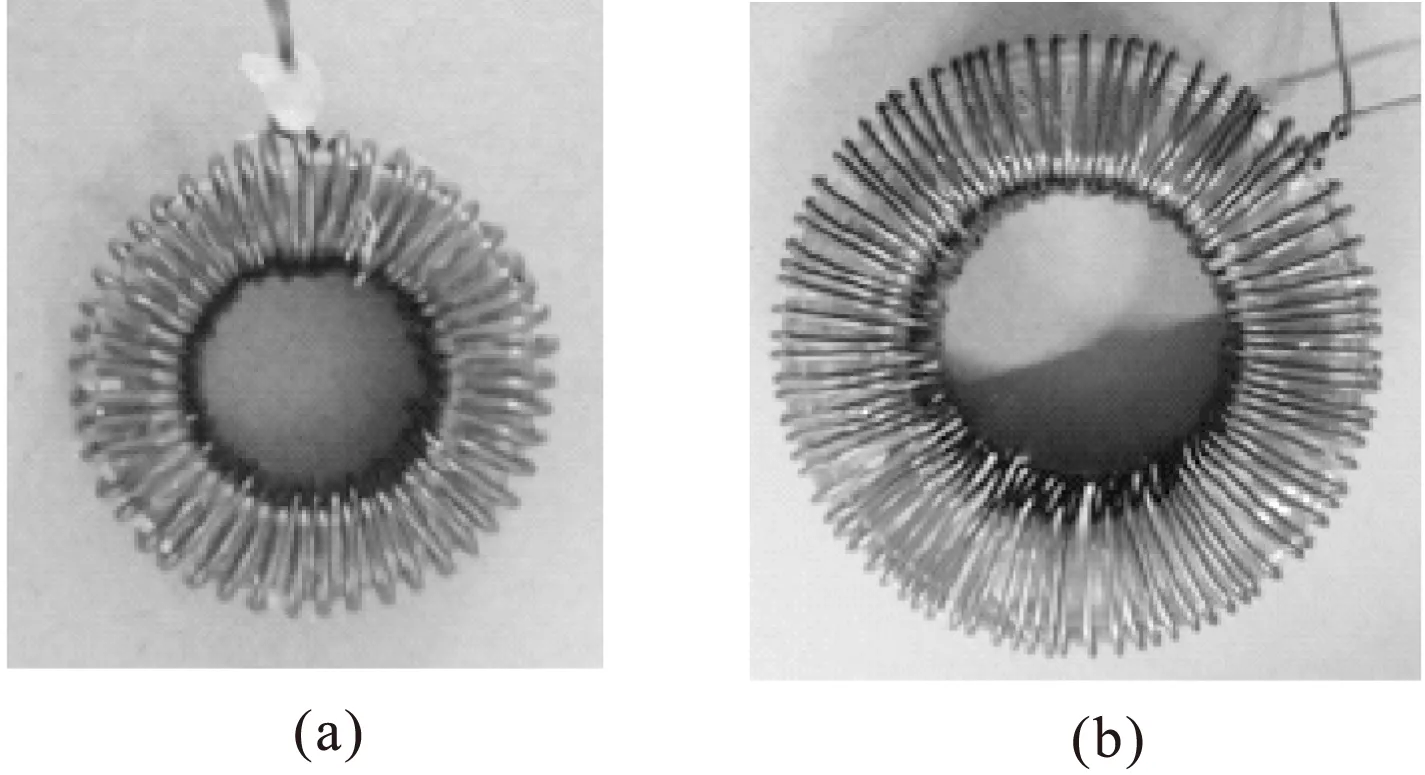
上下层的绕组损耗与内外层的绕组损耗相当,但是与内外层的绕组相比,上下两层的绕组的空间分布具有三维特征,不易计算。若将磁环展开,虽然可以简化为二维模型,但是改变了磁场分布。绕组损耗的根源在于磁芯的磁压降产生漏磁场,漏磁场切割绕组产生涡流,引起损耗。因此,将磁芯去除,引入等效电流元,用电流来代替磁芯的磁压降。将环形电感沿半径ρ(R1<ρ 磁芯的总磁压降为NI,均匀分布到每个电流元上,可以得知电流元的电流为I。磁芯展开后建立仿真模型,磁力线分布如图8所示。从图8可以看出,在A1和A3区域磁力线不满足绕组上实际的磁场分布。中间区域A2,磁力线分布和实际的磁场分布基本一致。为减小端部磁场对中间导体的影响,导体数量应该足够多,考虑到对称性,若电感绕组匝数为N匝,展开后用N+1匝来等效。可以计算导体1的损耗来表征任意一匝的绕组损耗。 为了方便计算,将线径为d的导体等效为边长为d的正方形导体,如图9所示。在导体上各个边均匀取多个点计算磁场。 图8 上下层绕组的周围磁场分布 图9 圆形导体等效为正方形导体 由于所有导体的电流均为z方向,采用磁矢位A作为中间变量。在直角坐标系下,源点坐标为(x0,y0),场点坐标为(x,y),那么磁矢位A可以表示为: (13) 上式中R0表示磁矢位参考点与坐标原点的距离。通过对磁矢位求旋度即可得到场点(x,y)处的磁场强度。 (14) 通过三次样条插值可以得到等效导体四个边上的磁场强度。插值法得到的磁场强度和仿真的磁场强度如图10所示。 图10 仿真和计算的磁场强度 从图10可知,导体1四周的磁场具有二维特征,除了很强的x方向磁场外,y方向磁场同样不可忽略在。因此,有必要采用二维的Dowell模型计算。当导体四周的磁场是位置的函数时,采用Dowell模型无法得到解析解,为了方便计算,各个边的磁场强度分别用平均值来表示,即: (15) 图11 两维Dowell模型 磁环在某一固定半径ρ下展开,导体1四个边的磁场方向如图11(a)所示。在H1x和H3x作用下,感应电流只是关于y的函数;在H2y和H4y作用下,感应电流只是关于x的函数。因此,可以将x方向磁场和y方向磁场分别考虑,导体内部的电流密度可以看成是直流的电流密度JDC加上x方向和y方向磁场产生的感应电流的电流密度Jy(x)和Jx(y),即。 J(x,y)=Jy(x)+Jx(y)+JDC (16) 取图11(b)中的安培环路,可以得到方程: (17) 对式(17)求两次导数可以得到: (18) 根据法拉第电磁感应定律和媒介方程: (19) 带入式(18)可以得到电流密度和磁场强度的方程: (20) 式(20)中,γ是修正的电导率, (21) 给定边界条件: (22) 可以算出电流密度Jy关于x的函数: (23) 同理,根据图11(c)可以得到x方向磁场产生的感应电流Jx(y): (24) 假设导体在R1和R2之间等分成M份,上下两个面的绕组损耗可表示为: (25) 磁环高度h为5mm,线径d为0.9mm,导体与磁芯的间距δ为0.2mm,给定每匝导体之间的间距为1.4mm。在频率20~500kHz范围内,导体1的单位长度损耗的仿真值和计算值如图12所示。 图12 导体1的单位长度电阻 电感除了绕组损耗外还包括磁芯损耗,直接测量电感的电阻实际上是包括磁芯损耗的等效电阻,因此很难得到实际的绕组电阻。然而,空心环形电感和带磁芯环形电感的磁场分布基本一致,绕组损耗相差微小。因此,可以采用空心环形电感的绕组电阻来替代实际的电感电阻,也不会引入磁芯损耗的影响。图13(a)是绕制的空心电感。内径8.58mm,外径13.85mm,高度8.12mm,采用线径0.9mm的漆包线均匀绕制46匝。图13(b)是内径16.77mm,外径28.63mm,高度16mm,采用线径0.9mm的漆包线均匀绕制87匝。在频率20kHz至500kHz时,测量和计算的绕组电阻分别如图14(a)和(b)所示。 图13 空心电感 从图14可以看出,在频率20kHz~1MHz范围内(即线径和集肤深度的比值在2~13之间),最大误差在15%以内。 磁性元件的绕组损耗是影响开关电源效率的重要因素。本文首先从直角坐标系和柱坐标系下的一维铜箔模型推导绕组损耗的数学模型。接着分析环形电感的绕组损耗,分为两个部分计算。 图14 空心电感电阻测量值和计算值 内外层的绕组损耗基本满足柱坐标系下的一维铜箔模型,当绕组绕制较为紧密的时候,采用柱坐标系下的Dowell模型计算不至于带来较大的误差。 直接计算上下层的绕组损耗难度较大,通过用电流元代替磁芯磁压降的方法将磁环展开成二维结构。采用二维Dowell模型计算中间一匝的绕组损耗。 实验验证表明,通过该方法可以估算出绕组的电阻,并且误差可以控制在15%以内。误差来源主要有两个部分:一是模型本身存在误差,尤其是计算外层绕组损耗,该模型误差较大。二是手工绕制的电感各匝之间的间距不均匀,影响实验结果。 [1] P.L.Dowell.Effects of eddy currents in transformers windings[J].Proc.IEEE,1966,113(8):1387-1394. [2] 旷建军.开关电源中磁性元件绕组损耗的分析与研究[D].南京航空航天大学,2007. [3] CHEN Wei,HUANG Xiaosheng,ZHENG Juanjuan.Improved Winding Loss Theoratical Calculation of Magnetic Component with Air-gap[C].IEEE PEMC,Harbin,China,2012:471-475. [4] Ningning Wang,Terence O′Donnell,Cian O′Mathuna.An Improved Calculation of Copper Losses in Integrated Power Inductors on Silicon[J].IEEE Trans.On powerelectronics,2013,28(8):3641-3647. [5] Roberto Prieto,José A.Cobos,Oscar García,Pedro Alou,Javier Uceda.Study of 3-D magnetic components by means of “double 2-D” methodology[J].IEEE Trans.on Industrial Electronics,2003,50(1):183-192. [6] SJ 2281-88.磁性氧化物或铁粉制成的环形磁芯的尺寸[S]. [7] 叶建盈,陈为.一种有气隙磁元件高频绕组损耗的测量评估方法[J].中国电机工程学报,2015,35(7):1749-1755. [8] 王传荣,朱玉灿,徐荣聪.大学数学(三)[M].北京:科学出版社,2007:228-232.


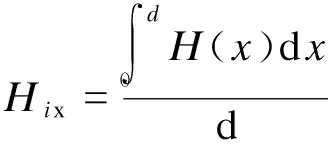
4 实验验证
5 结语